木结构螺栓连接的力学性能分析

王笑婷,牛 爽,祝恩淳

(1.哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150090;2. 哈尔滨工业大学 海洋工程学院,山东 威海 264209)

木结构的连接,通常先在工厂预制构件,后在施工现场通过连接件组装后实现。木结构的连接形式多种多样,其中螺栓连接应用较为广泛。螺栓连接的承载力和刚度难以做到与构件等同,具有显著的半刚性特性。螺栓连接的力学性能受众多因素影响,如螺栓的强度、直径,木构件的销槽承压性能、厚度,制作工艺和安装精度等。螺栓连接的承载力可通过欧洲屈服模式[1]计算,该屈服模式已被许多国家的设计标准所采用,例如欧洲规范Eurocode 5[2]、美国规范NDS:2015[3]和我国标准GB 50005—2017[4]。对于螺栓连接的刚度计算问题,我国木结构类技术规范中尚未给出明确的解决方案,国内外规范也缺乏一致的计算方法。Soltis等[5]对花旗松进行了螺栓连接试验,回归得到了连接节点刚度和螺栓直径之间的经验公式,试验结果表明:横纹受力时的连接刚度约为顺纹受力时的1/2。Rahim等[6]分析了螺栓直径、数量、端距和间距，木构件的厚度和密度等因素对钢夹板螺栓连接刚度的影响,并通过回归得到了连接刚度的经验公式。徐德良等[7]对钢夹板群栓连接进行了试验,连接刚度与螺栓列数、每列的螺栓数和螺栓的排布有关。Xu等[8]考虑了螺栓直径、木构件厚度和受力方向3个因素对钢填板螺栓连接的影响,通过回归分析对欧洲规范Eurocode 5中的滑移模量进行了修正。Cao等[9]对顺纹和横纹受力下钢填板螺栓连接的力学性能进行了试验研究,并基于欧洲规范Eurocode 5和Foschi模型提出了荷载-位移曲线的计算模型。Gauß等[10]考虑了螺栓数量、加载角度和加固措施对钢填板螺栓连接的影响,试验结果表明:欧洲规范Eurocode 5计算得到的滑移模量比试验值大约45%。Sandhaas等[11]对木-木螺栓连接和钢填板螺栓连接进行了试验研究,结果表明:欧洲规范Eurocode 5计算得到的滑移模量仅考虑了螺栓直径和木构件密度两个变量的影响,难以准确预测螺栓连接的初始刚度。

综上所述,对试验数据进行回归分析所得到的连接刚度计算公式具有一定的局限性,且缺乏一定的理论基础。由于木结构连接设计的多样性和复杂性,难以通过单一的经验公式来解决连接刚度的计算问题。鉴于此,本文基于弹性地基梁理论,推导得到了螺栓连接初始刚度的计算方法,并建立了螺栓连接荷载-位移曲线的数学模型,通过螺栓连接试验结果来验证数学模型的正确性和适用性。

1 弹性地基梁理论

螺栓视为梁,销槽木材视为地基,则在弹性阶段螺栓与销槽之间的关系类似于作用在弹性地基上的梁。Winkler[12]于1867年提出了弹性地基梁理论(BEFT),即假设地基表面任一点的沉降与该点单位面积上所受的压力成正比。Kuenzi[13]首先将弹性地基梁理论应用于木结构钉连接和螺栓连接的承载力计算中,该理论还可应用于木-混凝土连接中,具有广泛的适用性[14-15]。将销槽木材视为非线性地基时,通过数值方法还可得到连接节点的荷载-位移曲线[16-18]。在弹性阶段,双剪连接(图1)中部和边部木构件中螺栓(即梁)挠曲线微分方程分别如式(1)和(2)所示。

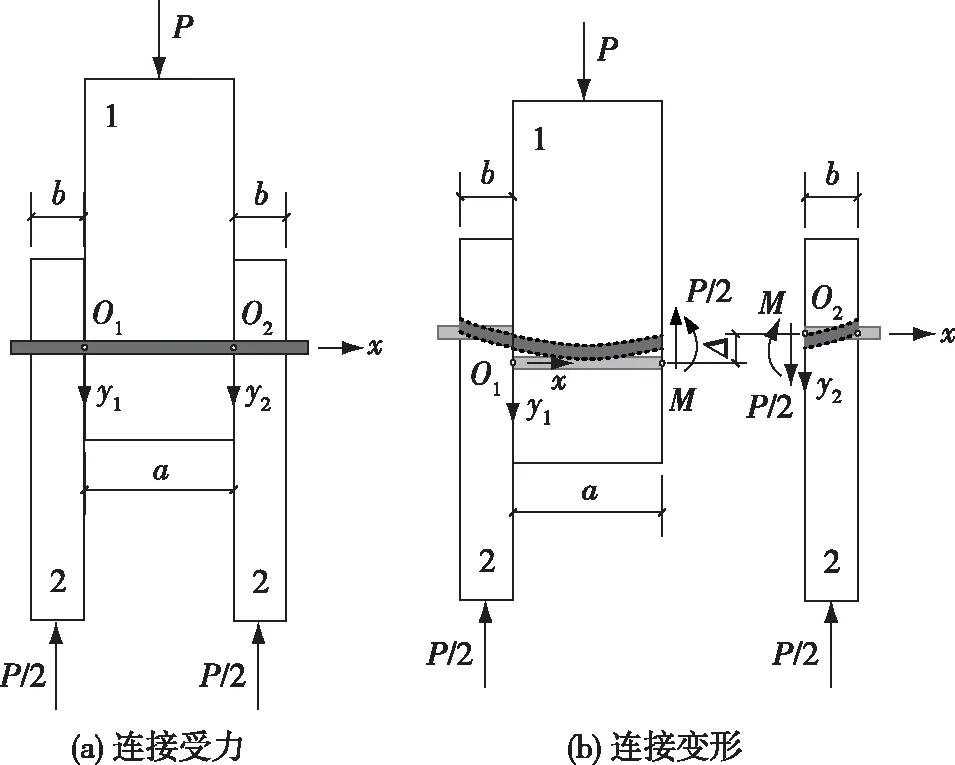
注：P为连接上的荷载，Δ为螺栓连接的相对变形，M为中部构件和边部构件交界面处梁截面上的弯矩，a为中部构件厚度，b为边部构件厚度，y1和y2分别为梁在中部和边部构件中的挠度,x为梁截面所处的位置,1和2分别代表中部构件和边部构件。

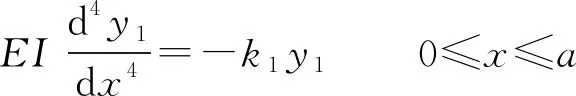
(1)

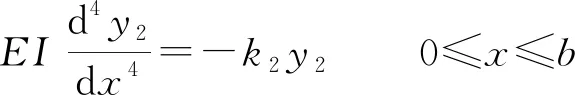
(2)

式中:E为梁的弹性模量,I为梁的抗弯刚度,k1为中部构件的地基模量,k2为边部构件的地基模量。

式(1)和(2)可改写为

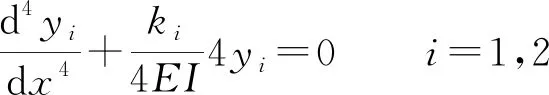
(3)

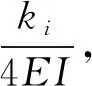
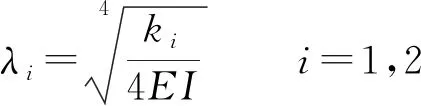
(4)

式中:λi为与螺栓和销槽的弹性有关的综合性参数,对螺栓的受力特性和变形特性具有重要影响。

式(3)的通解可表示为

yi=eλix[Aicos(λix)+Bisin(λix)]+

e-λix[Cicos(λix)+Disin(λix)]i=1,2

(5)

式中:Ai、Bi、Ci和Di为待定常数。

由梁的挠曲线方程yi求得剪力方程(Qi)、弯矩方程(Mi)和转角方程(θi),即可通过边界条件和连续条件(式(6)—(14))求解待定系数。

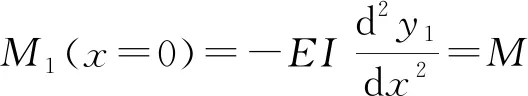
(6)

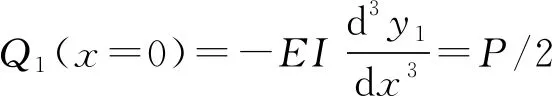
(7)

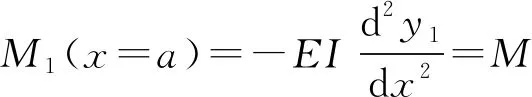
(8)

(9)

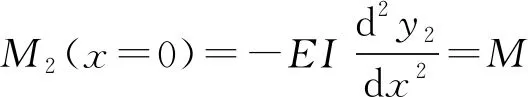
(10)

(11)

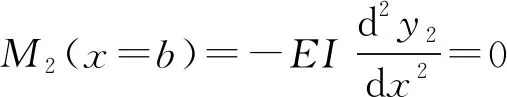
(12)

(13)

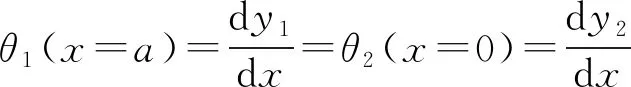
(14)

求得挠曲线y1和y2后,将两个木构件在交界面处的销槽变形相加可得到连接的相对变形(Δ)。将P除以Δ,即可得到连接在弹性阶段的刚度(KBEFT),见式(15)。

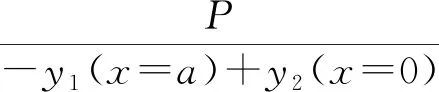
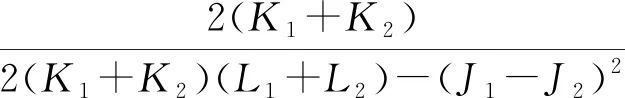
(15)

式中:参数L1、L2、J1、J2、K1和K2可由式(16)—(21)计算得到。

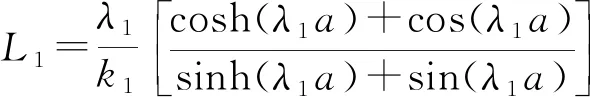
(16)

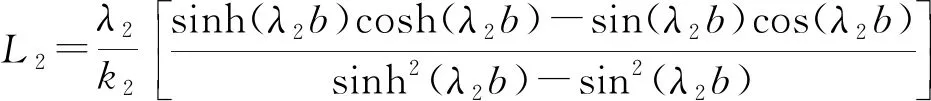
(17)

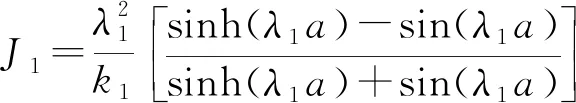
(18)

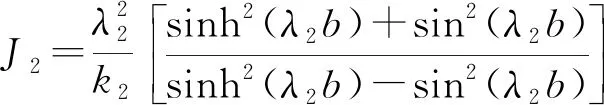
(19)

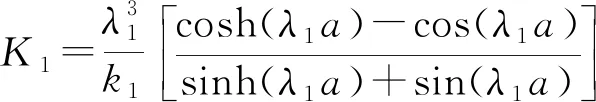
(20)

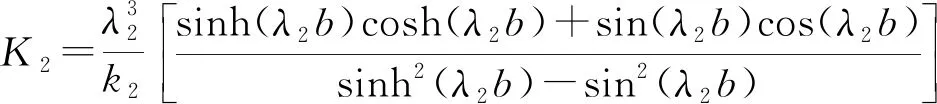
(21)

2 试验及刚度经验公式

为得到符合我国木结构设计标准中可靠度要求的螺栓连接承载力计算公式,文献[19]进行了大量的销槽承压试验和螺栓连接试验,并建议使用考虑螺栓塑性不充分发展得到的销槽承压有效长度系数及螺栓连接承载力计算公式。本文将在文献[19]得到的试验结果基础上针对连接的变形性能做进一步研究。

2.1 销槽承压试验

销槽承压试验所用树种为樟子松(Pinussylvestrisvar.mogonica)和东北落叶松(Larixgmelini(Rupr.) Rupr.),文献[19]共进行了390个试件的销槽承压试验,钢销真实直径(d)为12、14、16和18 mm。试验结束后对试件的含水率和气干密度进行测定,并换算为全干相对密度[20]。在螺栓连接中,销槽承压刚度即为弹性地基梁理论中的地基模量。销槽承压刚度由单位长度上的荷载-位移曲线确定,取弹性阶段的斜率为销槽承压刚度(k)。两种木材的销槽承压强度、刚度和全干相对密度列于表1。

2.2 销槽承压刚度经验公式

连接刚度计算方法的准确性主要取决于销槽承压刚度的取值[21]。已有研究表明销槽承压刚度与木材密度、销直径及荷载作用方向与木纹方向的夹角有关[22-23]。经非线性拟合得到顺纹和横纹受力时的销槽承压刚度与Sd、d的关系式(式(22)和(23))。樟子松和东北落叶松顺纹受力时的销槽承压刚度约为横纹受力时的3倍。

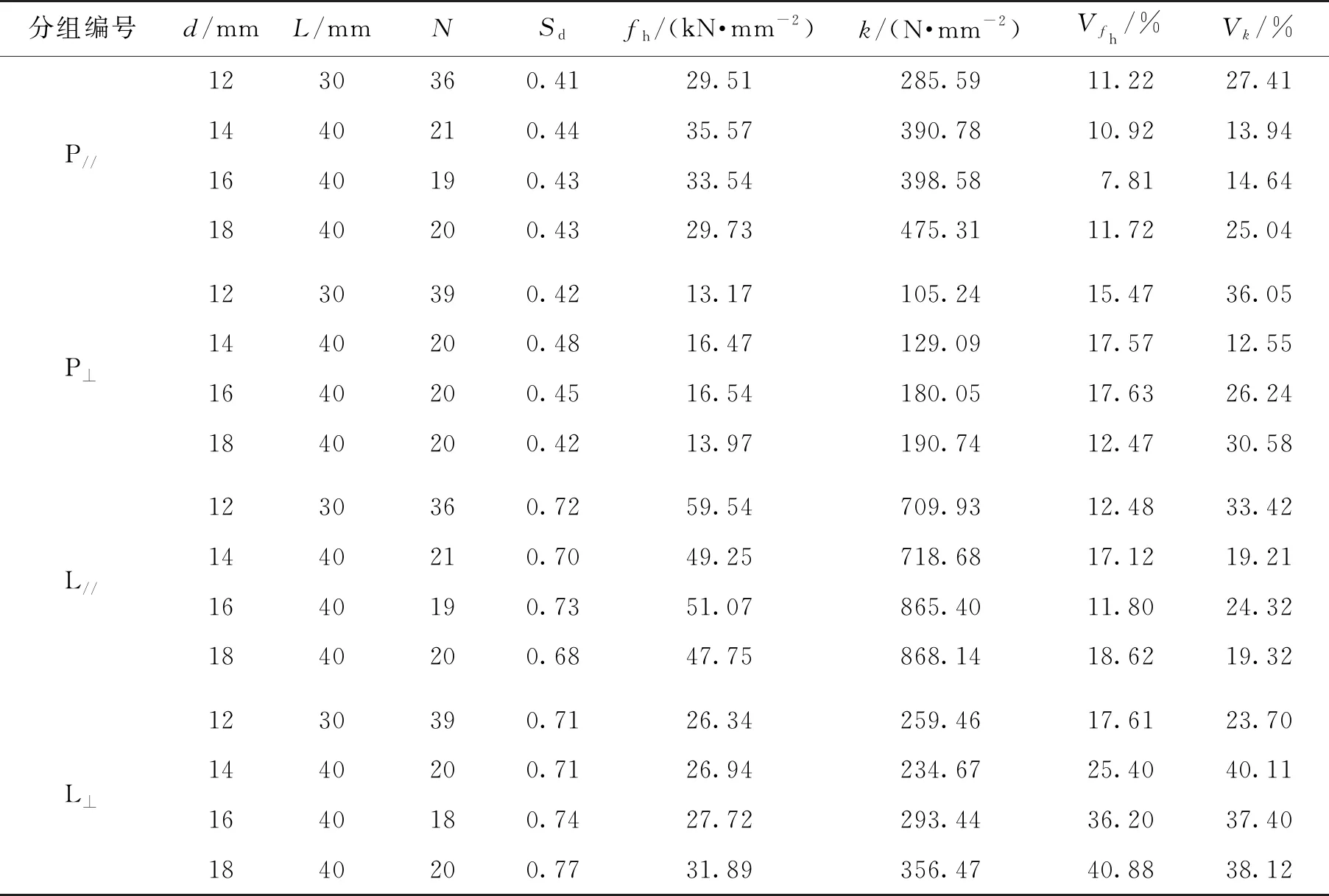
表1 销槽承压强度、刚度和全干相对密度试验结果

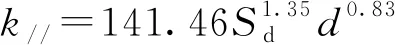
(22)

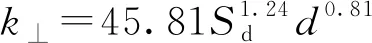
(23)

2.3 螺栓连接试验

螺栓连接双剪试验中采用的木材与销槽承压试验中的保持一致。螺栓名义直径(Dn)为12、16和18 mm,真实直径(De)对应为10.5、14.5和16.2 mm,螺栓的强度等级为Q235,平均屈服强度为243.45 MPa。本文采用了不同的树种和构件厚度组合的试件进行试验以符合双剪连接的4种屈服模式，每种组合包含3个试件,文献[19]共进行了144个试件的螺栓连接试验,并在试验结束后分别测得中部和边部构件的全干相对密度。荷载-位移曲线在弹性阶段的斜率为螺栓连接在正常使用极限状态下的初始刚度(Ks)。将弹性阶段拟合得到的直线偏移5%d后与荷载-位移曲线的交点定义为屈服点；对于两者不相交的情况,则取最大荷载所对应的点为屈服点。屈服点对应的荷载即为屈服荷载(Py)。不考虑滑移阶段,本文将屈服点对应的割线刚度定义为承载能力极限状态下的螺栓连接刚度(Ku),将塑性阶段的斜率定义为连接的屈服后刚度(Kp)。表2列出了螺栓名义直径为18 mm时的试验结果。

3 结果与分析

3.1 螺栓连接试验与计算结果对比

在正常使用极限状态下,欧洲规范Eurocode 5通过每销每剪面的滑移刚度(Kser)来计算连接的变形,螺栓连接滑移刚度(即连接初始刚度)的计算式为

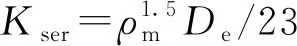
(24)

式中:ρm为木材的平均密度,kg/m3。

式(24)仅考虑了木材密度和螺栓直径对连接初始刚度的影响。欧洲规范Eurocode 5规定承载能力极限状态下的连接刚度可取2/3Kser。通过试验结果可知,当螺栓名义直径为12、16和18 mm时,两种极限状态下刚度的平均比值(Ku/Ks)分别为0.701、0.683和0.673,与Eurocode 5中相关规定基本一致。由式(22)和(23)可知：通过中部和边部构件的全干相对密度可计算得到相应的销槽承压刚度,即可通过弹性地基梁理论计算得到连接初始刚度。以螺栓名义直径为18 mm为例,将分别按弹性地基梁理论和欧洲规范Eurocode 5计算的连接初始刚度列于表3,并与试验结果进行对比。

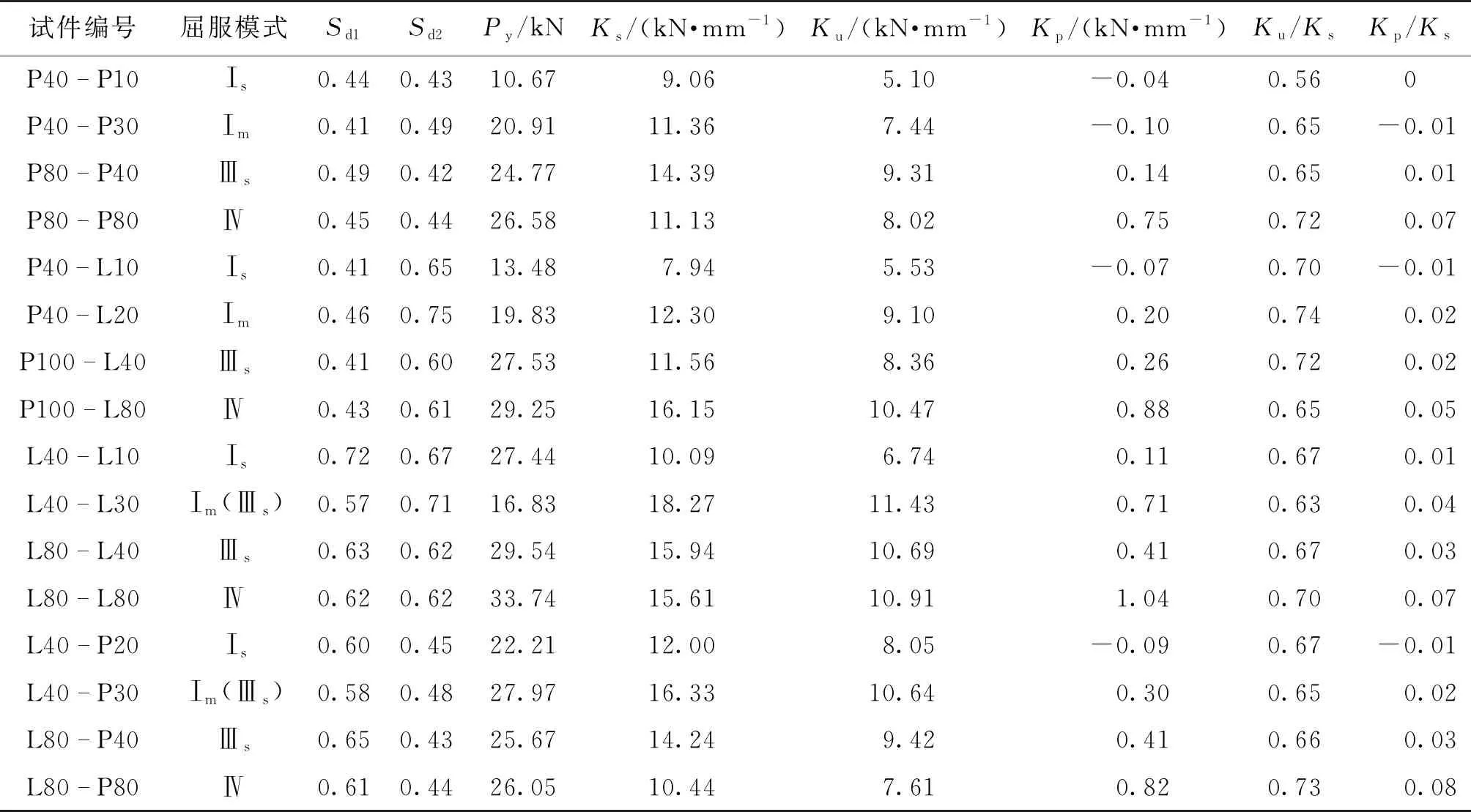
表2 螺栓连接承载力和刚度试验结果(Dn=18 mm)

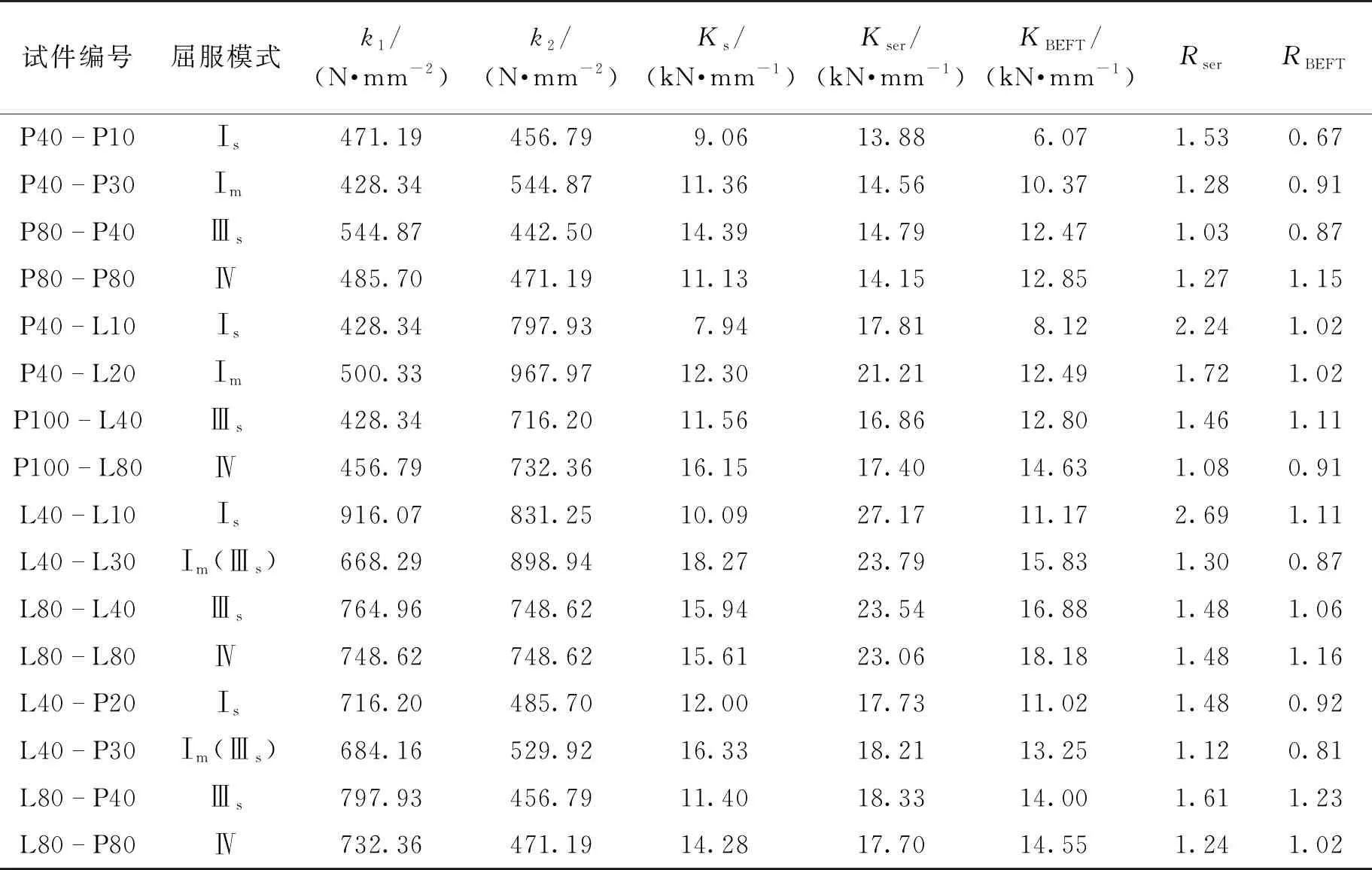
表3 连接刚度计算结果与试验结果对比(Dn=18 mm)

以连接初始刚度的试验值(Ks)为横坐标,理论方法得到的初始刚度计算值(Kser或KBETF)为纵坐标,可得到图2。由图2可知：数据点越接近对角线说明计算值越接近试验值。根据欧洲规范Eurocode 5得到的数据点大多位于对角线上方,校验系数的平均值为1.687,说明在多数情况下欧洲规范Eurocode 5高估了连接初始刚度。除少数情况外,根据弹性地基梁理论得到的数据点更均匀地分布在对角线的两侧,校验系数的平均值为1.046,弹性地基梁理论计算结果和试验结果吻合更良好。

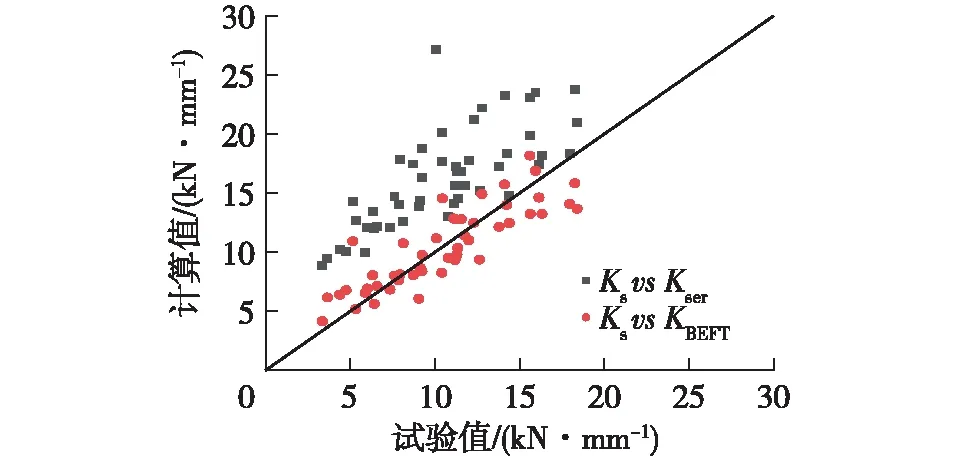
图2 连接初始刚度试验值和计算值的对比

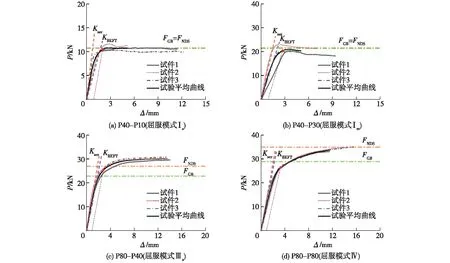
图3 连接初始的荷载-位移平均曲线

文献[19]考虑圆钢销塑性的不充分发展并引入钢材的弹塑性强化系数,采用欧洲屈服模式推导出连接承载力计算式,并被GB 50005—2017所采用。美国规范NDS: 2015在计算连接承载力时考虑了圆钢销塑性的完全发展和钢材的强化。以边部和中部构件均为樟子松且螺栓名义直径为18 mm的试件为例,将文献[19]中连接承载力以及本文初始刚度计算值示于图3,图3中试验荷载-位移平均曲线上的红点为由偏移法确定的屈服点,绿色和橙色点划线分别对应于GB 50005—2017计算得到的连接承载力(FGB)和美国规范NDS: 2015得到的连接承载力(FNDS)。

螺栓连接的屈服模式分为木材发生销槽承压破坏(屈服模式Ⅰm和Ⅰs)和螺栓形成塑性铰(屈服模式Ⅲs和Ⅳ)两种情况。由图3可见:对于屈服模式Ⅰm和Ⅰs,欧洲规范Eurocode 5计算得到的连接初始刚度远高于试验值。对于屈服模式Ⅰs,由弹性地基梁理论得到的连接初始刚度略低于试验值;对于屈服模式Ⅰm,由弹性地基梁理论得到的连接初始刚度则和试验值相吻合。对于屈服模式Ⅲs和Ⅳ,欧洲规范Eurocode 5的连接初始刚度计算值略高弹性地基梁理论的,两者和试验曲线差别不大。由于欧洲规范Eurocode 5仅考虑了木材平均密度和螺栓直径的影响,而使得在不同木构件厚度的情况下计算得到的连接初始刚度均是相同的。由此可见,欧洲规范Eurocode 5中的连接初始刚度经验公式在应用时具有一定的局限性,仅适用于木构件厚度较大的情况,这类螺栓连接通常将在加载后期易形成塑性铰(屈服模式Ⅲs和Ⅳ)。

当发生销槽承压破坏时,屈服后刚度(Kp)接近于0,通过偏移法得到的屈服荷载即为连接的极限荷载。此时GB 50005—2017和美国规范NDS: 2015计算得到连接承载力是相同的,与试验值相吻合。当螺栓形成塑性铰时,荷载-位移曲线的弹塑性阶段变长。屈服模式Ⅲs在塑性阶段荷载增量逐渐减小,试验得到的Kp/Ks为0.03。屈服模式Ⅳ在塑性阶段荷载仍持续增长,直至连接破坏时仍具有一定刚度,Kp/Ks的平均值为0.07。由于两种规范对螺栓屈服弯矩的处理方法不同,使得美国规范NDS:2015计算得到的承载力高于GB 50005—2017计算得到的,同时也高于由偏移法得到的承载力,这表明考虑销塑性完全发展和钢材强化的计算高估了连接承载力。

3.2 荷载-位移曲线拟合

螺栓连接的荷载-位移曲线充分反映了连接的受力性能。二折线模型可用于拟合螺栓连接的荷载-位移曲线(图4)。二折线模型的关系式为

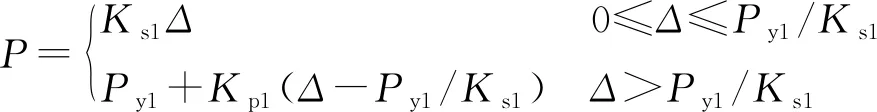
(25)

式中:Ks1为第一段折线的斜率,Kp1为第二段折线的斜率,Py1为分段点对应的荷载。

图4 二折线模型

Foschi[24]提出了一种三参数模型用于拟合螺栓连接的荷载-位移曲线(图5)。该模型的关系式为

P=(Py2+Kp2Δ)(1-e-Ks2Δ/Py2)

(26)

式中:Ks2为曲线在原点处的斜率,Kp2为曲线渐近线的斜率,Py2为渐近线与P轴的交点对应的荷载。

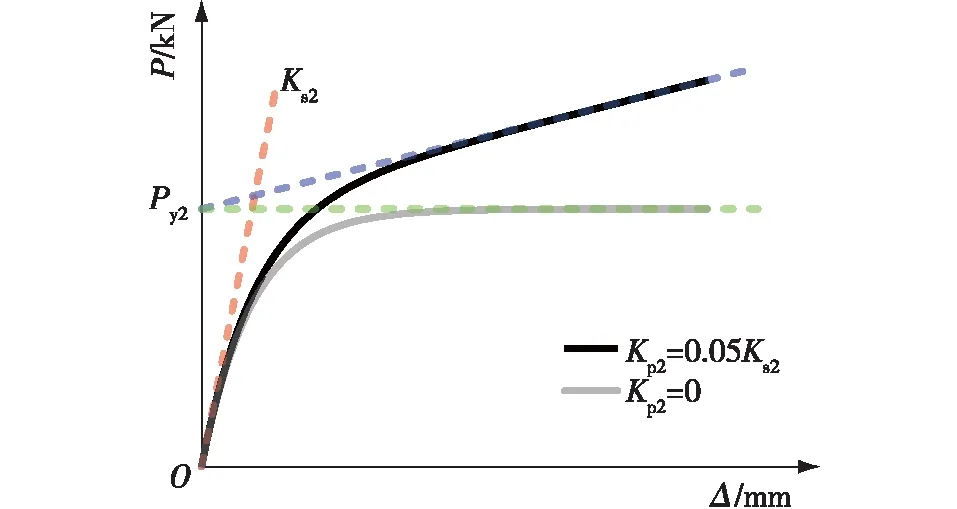
图5 Foschi模型

Attiogbe等[25]提出了一种四参数模型用于描述钢结构中半刚性节点的弯矩-转角关系(图6)。本文将该数学模型运用于螺栓连接的荷载-位移曲线的拟合,该模型中参数Ks3、Kp3和Py3的含义与Foschi模型中的Ks2、Kp2和Py2相同,另可通过形状参数(n)来调整曲线弹塑性阶段的形状，如式(27)所示。

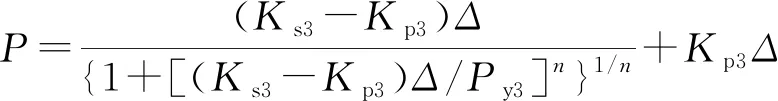
(27)

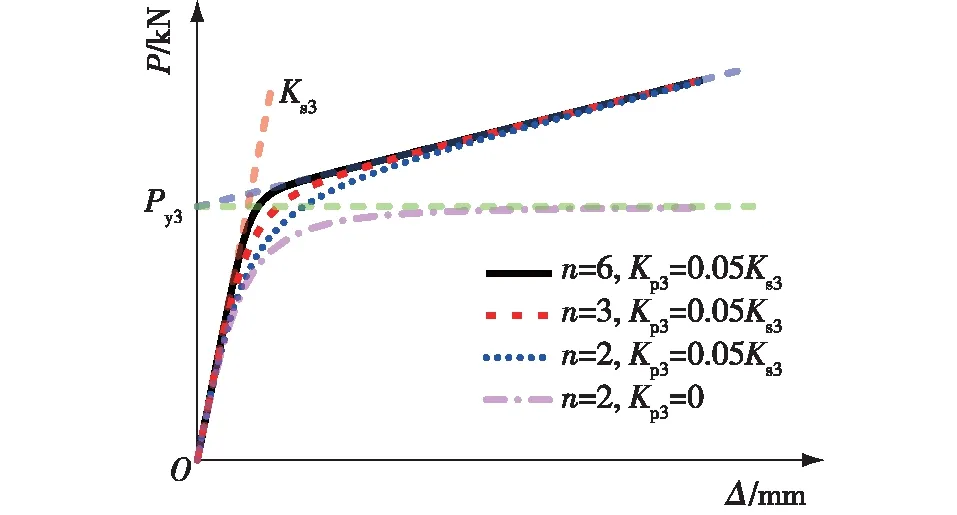
图6 Attiogbe模型

仍以边部和中部构件均为樟子松且螺栓名义直径为18 mm的试件为例,用上述3种数学模型对试验得到的荷载-位移曲线进行拟合(图7)。拟合得到的参数Pyi、Ksi和Kpi(i=1,2,3)分别对应于螺栓连接的荷载、初始刚度和屈服后刚度。由图7可知：3种模型均能较好地描述螺栓连接的荷载-位移关系,二折线模型在弹塑性阶段与试验曲线有所偏差,Attiogbe模型的平均拟合系数(R2=0.98)略高于Foschi模型的(R2=0.97)。对于屈服模式Ⅰs和Ⅰm,3种模型拟合得到的荷载Py1、Py2和Py3与螺栓连接承载力试验值一致;对于屈服模式Ⅲs和Ⅳ,由于模型和试验对于屈服荷载的定义有所不同,使得拟合得到的荷载略高于试验值。Attiogbe模型拟合得到的连接初始刚度Ks3和二折线模型的基本一致,而二折线模型的连接初始刚度Ks1和试验值相同。对于Foschi模型,由于该模型在原点附近曲率变化较大,拟合得到的初始刚度Ks2约为试验值的1.5倍。

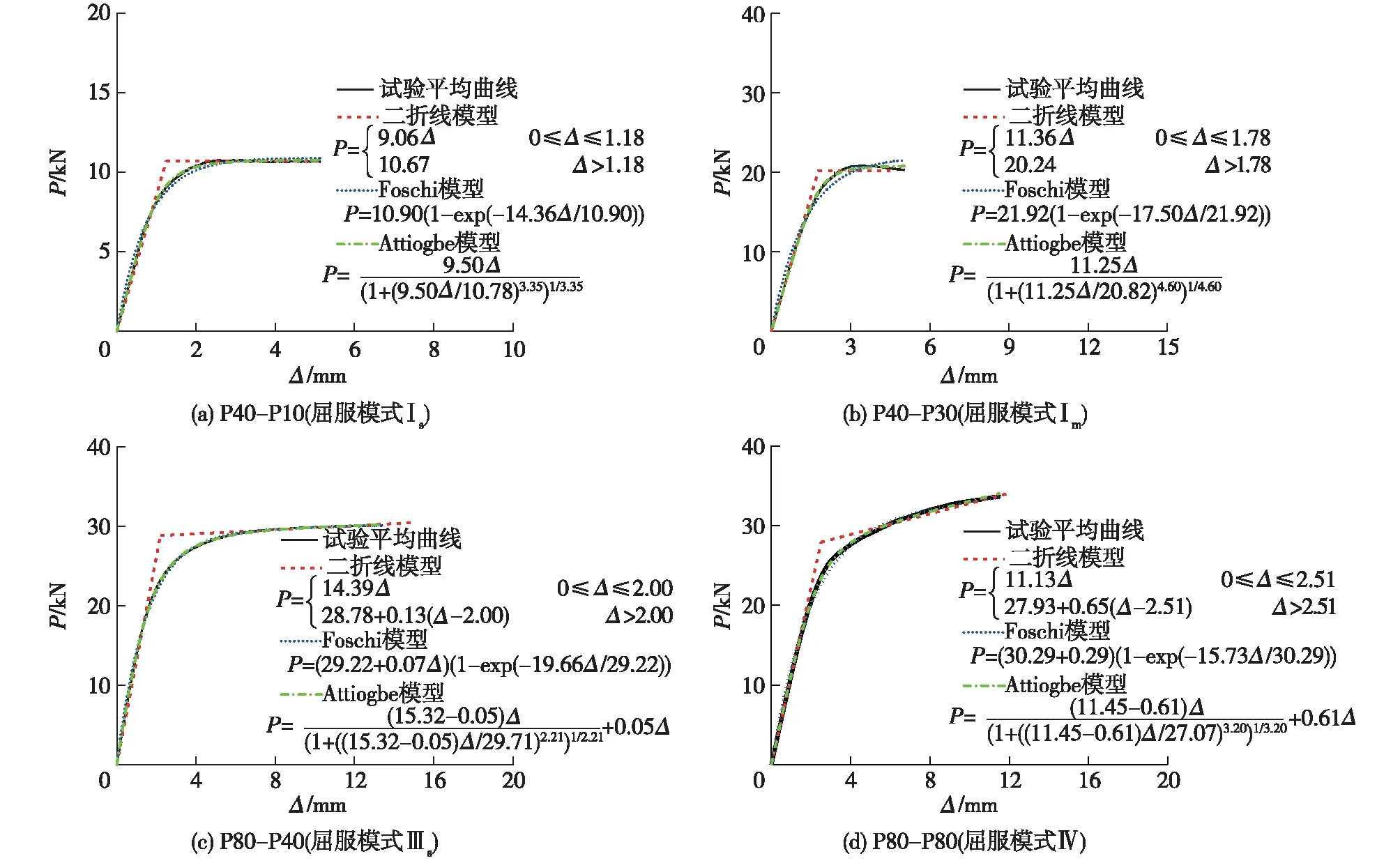
图7 荷载-位移曲线的拟合

3.3 荷载-位移曲线理论计算模型

通过弹性地基梁理论可计算得到连接初始刚度(KBEFT),通过GB 50005—2017可得到连接的承载力(FGB)。已有试验结果表明：对于屈服模式Ⅰs和Ⅰm,屈服后刚度可取0;对于屈服模式Ⅲs和Ⅳ,可分别取连接屈服后刚度与初始刚度的比值为0.03和0.07。对于Attiogbe模型,对所有试验数据拟合可得到各屈服模式下的形状参数(n)的平均值分别为6.5(屈服模式Ⅰm和Ⅰs)、2.5(屈服模式Ⅲs)和1.9(屈服模式Ⅳ)。由此，可通过理论计算的方法预测螺栓连接的荷载-位移曲线(图8)。

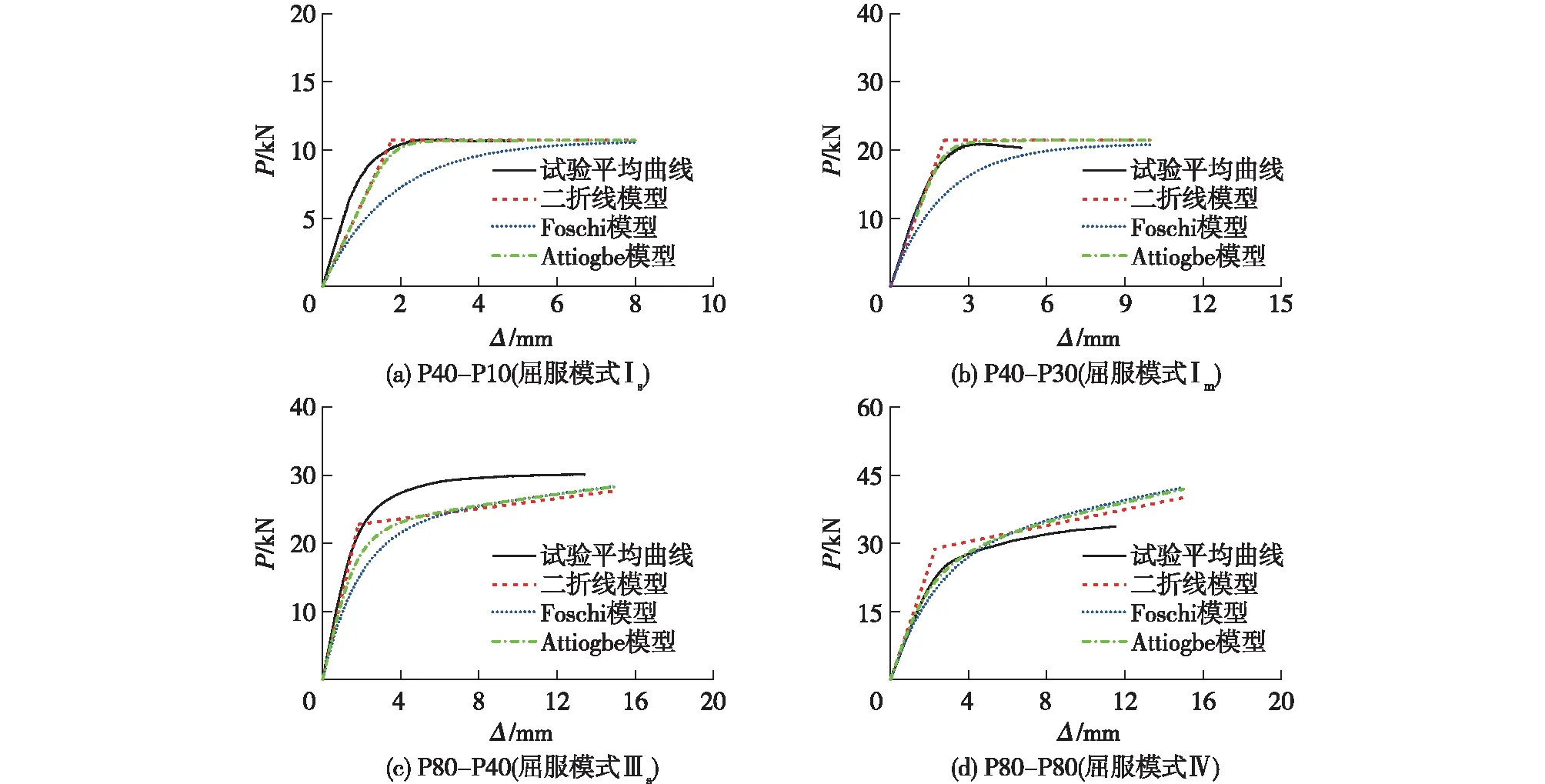
图8 理论计算模型预测所得荷载-位移曲线与试验结果对比

由图8可知:Foschi模型由于曲线形状的限制,使得曲率变化与试验曲线有所偏差,尤其在屈服模式Ⅰm和Ⅰs的弹塑性阶段上存在较大误差。Attiogbe模型可通过试验结果得到形状参数(n)的经验值来解决这一问题。二折线模型和Attiogbe模型相比于Foschi模型能更好地预测连接的荷载-位移曲线,其中二折线模型简洁直观,但存在刚度突变,而Attiogbe模型则能更好地反映连接的屈服过程,为整体结构抗侧性能的分析和计算提供可靠的依据。

4 结论

1)提出了销槽承压刚度用于计算螺栓连接的初始刚度。对销槽承压试验结果回归,通过全干相对密度和销直径两个变量,提出了计算顺纹和横纹受力销槽承压刚度的经验公式。

2)将弹性地基梁理论用于螺栓连接的初始刚度计算,可通过销槽承压刚度来计算连接的初始刚度。欧洲规范Eurocode 5的连接初始刚度计算结果的校验系数为1.687,而弹性地基梁理论计算结果的校验系数为1.046,验证了弹性地基梁理论刚度计算方法的正确性和适用性。定义了承载能力极限状态下的螺栓连接刚度,试验结果表明其值约为正常使用极限状态下初始刚度的2/3,这与欧洲规范Eurocode 5的规定相符。

3)将连接刚度和承载力的计算方法和Attiogbe四参数模型相结合,得到了螺栓连接的荷载-位移曲线计算模型,可用于整体结构的分析和计算。