高层建筑地震波动效应分析方法

康艳博,黄世敏,罗开海

(中国建筑科学研究院有限公司,北京 100013)

从设计方法的基本理念和侧重点来看,近现代抗震技术先后经历了基于强度、基于延性修正强度、基于位移、基于性能的抗震设计方法等[1-9]。然而,无论是早期基于强度的抗震设计方法还是目前较为热门的基于性能的抗震设计方法,建筑结构地震作用及响应的计算均是基于基底嵌固的封闭隔离体系采用牛顿第二运动定律进行的。其主要差别在于静力法将建筑简化为刚性体,动力法[10-13]考虑了建筑结构自身动力特性的影响。牛顿第二运动定律是经典的质点动力学方程,采用该方法求解结构体系的动力响应时,涉及到结构中连续分布质量如何离散为集中质量的问题。传统的做法是将竖向构件(墙、柱等)的分布质量向楼层位置集中,所有的竖向构件只有刚度,没有质量。按照固体力学的波动理论,此时竖向构件的振动传播速度趋于无穷大,造成构件上下两质点之间的传播时间为0,结构各楼层之间的地震响应分析结果同步,响应相位差为0。

然而,实际上建筑地震响应是地震地面运动的输入能量在建筑内以波动的形式不断传播、衍射、反射、折射和干涉的过程。建筑地震响应监测结果以及大量振动台试验结果均表明:在地震作用下建筑结构具有明显的波动效应特征,沿建筑高度方向具有时滞效应和驻波效应[14-17]。因此,在高层建筑迅猛发展形势下,亟待对现有高层建筑尤其是超高层建筑的结构振动抗震设计方法的适用性进行审视和探讨,寻求建立考虑结构波动效应特性的抗震分析方法,进一步完善建筑结构抗震理论。

康艳博等[18-19]对传统结构动力理论的局限性进行了分析和评述,并对高层建筑结构地震波动响应进行了理论探索和试验研究,对于特定的建筑,振动驻波的波腹位置由输入激励的高频分量确定,波节位置由低频分量确定。

为了进一步研究和探索高层建筑结构在地震地面运动激励下的波动响应机制和波动现象规律,本文总结北京国贸三期主楼、上海中心大厦、深圳平安金融中心3栋超高层建筑振动台模型试验的数据,对建筑结构的等效波速、等效波长进行研究,得出相应的估算公式。并基于高层建筑地震波动效应的驻波现象,对经典动力学理论的适用范围展开讨论。

1 高层建筑振动台试验

1.1 北京国贸三期主楼概况

建筑总高约330 m,地下3层、地上74层,首层平面尺寸约为55.3 m×55.3 m(图1)。

结构体系为筒中筒结构:内筒为型钢混凝土核心筒体、外筒为型钢混凝土框架筒体,核心筒在16层以下设有钢板剪力墙。

内外筒之间在第28层沿X向设有4个伸臂桁架,第56层沿X、Y向各设有4个伸臂桁架;外筒在第6～8、28～30和55～57层各设有3个两层高的腰桁架。

图1 北京国贸三期主楼结构示意图

1.2 试验方案

1.2.1 测量元件的布置

加速度传感器:模型基座形心处布置2个用于测量基座X、Y向加速度;腰桁架上下楼层质心轴线处布置2个用于测量楼层X、Y向加速度;其余楼层每隔4层在X、Y向各布置1个;在第16、42和64层楼层角部X、Y向各布置1个,与本楼层质心轴处的传感器联合使用,用于判断结构的扭转效应。

应变片:将37个应变片布置于底层内外筒钢混凝土竖向构件、腰桁架构件、伸臂桁架构件处。

1.2.2 动力相似比

试验模型的动力相似比见表1。

表1 北京国贸三期主楼动力相似比

1.3 波动现象分析

本文选取了3个振动台模型试验进行分析,试验工况如表2所示。

表2 振动台试验工况

图2—4分别为工况1—3下不同时刻的模型加速度响应曲线。由图2—4可知:不同工况下加速度响应的首波波峰到达时刻随着测点高度的增加而依次延后。同时,不同时刻各模型的加速度剖面与零基线基本上都存在交叉,即顶部与底部的加速度响应存在异向,这表明该模型加速度响应从底部向上存在明显的时滞效应。

从底部向上每隔一段高度的加速度廓线均出现“颈缩现象”,不同工况下“颈缩现象”出现的高度不同。模型顶部测点的数据表明不同工况下加速度在结构顶部存在“放大现象”。整体上,加速度廓线呈现波腹、波节交替出现的现象,加速度响应沿波传播方向存在明显的驻波效应。

图2 模型加速度响应曲线(工况1)

2 高层建筑振动台模型试验波动参数

2.1 等效波速(ce)

介质模型中波速(c)是波动理论分析最为关键的参数。均匀直杆介质的波速理论定义为[20]

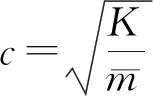
(1)

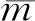
实际介质模型的受力变形并非单一变形,而是多种变形模式的复杂组合,包括剪切变形、弯曲变形、扭转变形等。因此,式(1)的预测结果往往与实测结果存在较大偏差。文献[19]依据建筑总高度(H)和基频(f1)得出了等效波速(ce)的估算方法,如式(2)所示。

ce=4Hf1

(2)

式(2)适用于一阶弯曲变形模态占主导地位的一维均匀直杆介质模型。但对于剪切变形和高阶模态影响不可忽略的超高层建筑模型来说,一阶模态难以有效反映结构的刚度属性,此时仍然采用一阶频率进行等效波速的估算,势必会导致估算数值偏小(表3)。

鉴于上述原因,引入第2频率的影响,对式(2)进行修正得到式(3)。

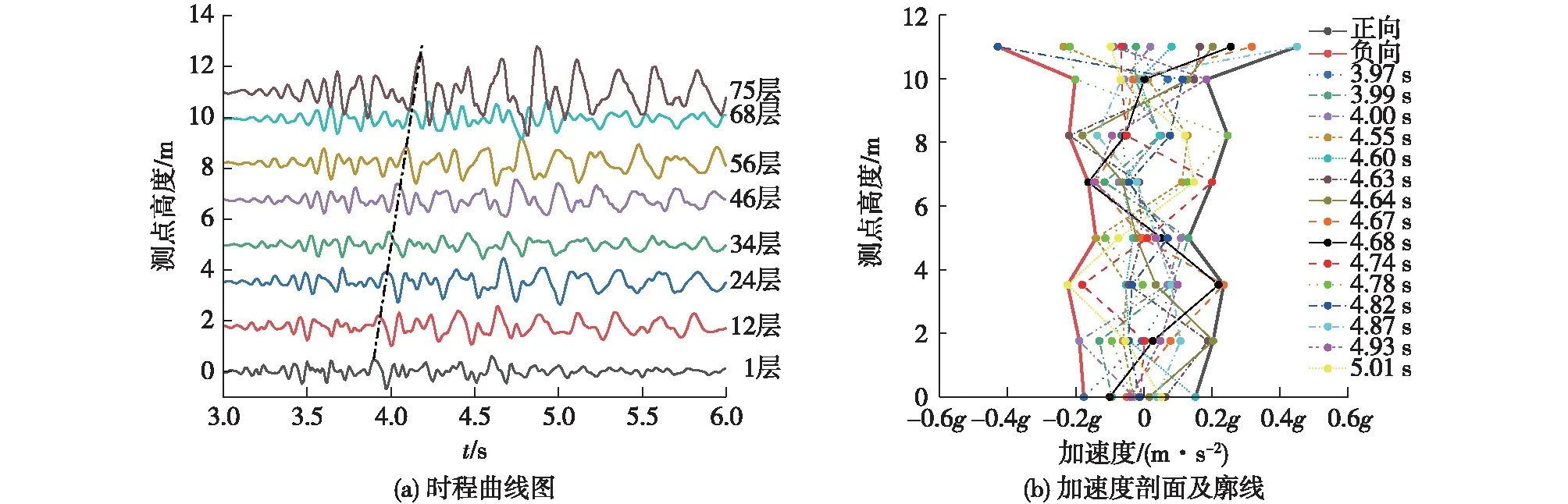
图3 模型加速度响应曲线(工况2)

图4 模型加速度响应曲线(工况3)

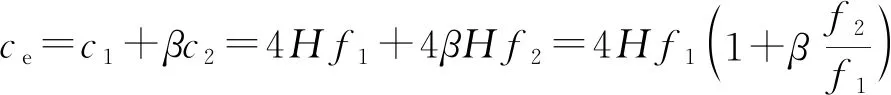
(3)

式中:f1、f2分别为结构的第1、2阶模态的振动频率,c1=4Hf1(第1频率波速),c2=4Hf2(第2频率波速)，β为频率调整系数。

将北京国贸三期主楼、上海中心大厦、深圳平安金融中心振动台模型试验的实测波速作为等效波速(ce),代入式(3)得到各模型的β,3个模型的β平均值为0.154。再将β平均值重新代入式(3),得到了修正后的各模型的估算等效波速(c′e)，该值与实测等效波速的误差很小,说明考虑第2频率的修正是可行的。

表3 3个超高层建筑振动台模型的等效波速

2.2 等效均布质量和等效刚度(Ke)

按照结构动力学的定义,结构各阶模态的振动频率(fi)为

(4)

式中:ki为第i模态广义单自由度体系对应的刚度,mi为第i模态广义单自由度体系对应的质量。

将式(1)和(4)代入式(3)可得

(5)

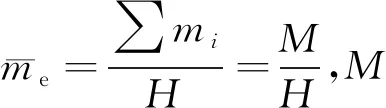
则式(5)可变为

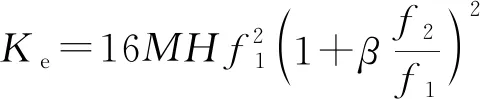
(6)

由式(6)可知:建筑结构的Ke可由M、H、f1、f2等参数进行估算。根据式(3)的推导思路,也可进一步将等效刚度的计算扩展到更多模态。

2.3 等效波长(λe)

介质对象在输入激励下沿传播方向除了存在明显的时滞效应外,还存在显著的驻波效应。同一个试验对象在相同的输入激励下,其波腹和波节的数量及位置是相对固定,这一现象与模型的等效波长密切相关,如式(7)所示。

(7)

式中：fe为输入激励的主控频率。

将式(3)代入式(7),可得

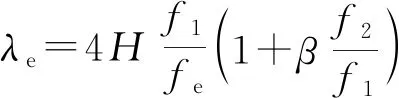
(8)

对于特定的建筑物,H、f1、f2均是定值,因此λe主要取决于fe。根据随机振动理论,结构底部的任一输入激励均可表示为一系列具有不同幅值(Ai)的三角脉冲的组合,即

p0=∑Aisin(2πfit+φi)

(9)

式中:p0为随机输入的激励,其频率成分是随机的,理论上介质模型应有无数个波长;φi为初始相位。

fe越大,λe越小。因此,高频输入时,波长短,波腹波节的数量会多;低频输入时,波长长,波腹波节的数量相对少,加速度廓线相对平缓。结合前述的试验结果与分析结论可知,输入激励中的高频部分决定了试验模型响应的波腹与波节的位置,低频部分往往对波节部位的“颈缩”程度起决定作用。因此,分析地震地面运动的高频部分对高层建筑结构波动响应的影响具有非常重要的理论意义和工程价值。国内外大量强震记录也表明,地震输入的大部分能量是由高频波构成的。

对于实际工程结构,当输入激励确定时,可采用式(9)对输入激励进行解构分析,即通过频谱分析确定fe,代入式(8)确定该输入激励下结构的λe。

当没有确定的输入激励时,可根据工程场地条件及地震环境情况,采用规范给出的反应谱平台段上限周期和下限周期对应的频率作为式(8)中的fe进行波长估算。根据GB 50011—2010《建筑抗震设计规范》的规定,反应谱平台段的起始周期为0.1 s;而末端周期即特征周期Tg主要与场地类别和设计地震分组有关,其取值为0.2～0.9 s。因此,地震激励的频率范围约为1～10 Hz。对于实际工程,可采用该范围的中值(5 Hz)进行波长估计,以便对建筑结构的波动效应进行初步评估,确定相对波腹与相对波节出现的高度位置,进而提出工程处理对策。

3 质点振动理论适用范围

理论上波节与波腹的位置分别如式(10)与(11)所示。

(10)

(11)

式中:λ为波长,Hjk为波节位置,Hfk波腹位置,k为正整数。

式(10)和(11)表明:波长确定的情况下,结构驻波效应的波腹总出现在1/4波长的奇数倍位置处,波节总出现在1/2波长的整数倍位置处。因此,当建筑物总高度不超过1/4波长时,建筑物在基底输入激励的作用下,沿高度方向自底部而上的加速度廓线逐渐增大,顶部加速度廓线最大。不同时刻的加速度剖面与零基线的交点很少,这与经典振动理论的响应分析结果基本一致。因此,可以推断基于质点振动理论的经典结构动力分析方法的适用范围是总高度不超过1/4波长的建筑,即

(12)

将式(8)代入式(12),可得

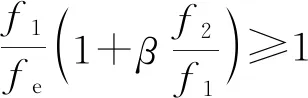
(13)

(14)

式(14)中Rf的值域范围需要根据大量试验数据统计进行进一步的分析与验证,通过已有的数据估算其值约为1.4～1.6。根据本文3个超高层建筑振动台模型试验数据得到的Rf平均值约为1.52,后续研究中Rf取1.50。当Rf的值域范围确定后,基于质点振动理论的经典结构动力分析方法的适用范围如式(15)所示。

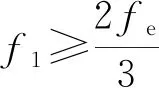
(15)

T1≤1.5Te

(16)

T1≤[T1]=1.5Tg

(17)

式中:[T1]为结构基本振动周期限值，T1为结构基本振动周期，Tg为反应谱特征周期,Te为输入激励的主控频率对应的周期。

按GB 50011—2010《建筑抗震设计规范》的规定,对于给定的工程场地,Tg是确定的。因此,经典结构动力分析方法可采用的范围如表4所示。

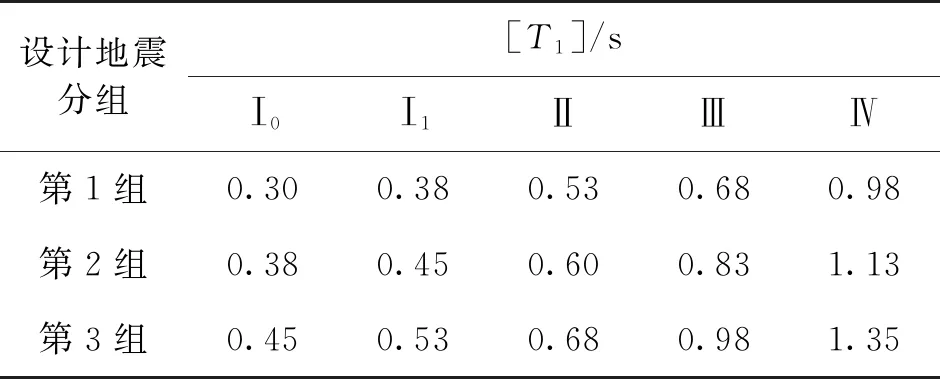
表4 经典结构动力分析的基本振动周期限值

根据湖南大学沈蒲生等[21]的研究,T1与H的关系为

(18)

将式(18)代入式(17),求解可得

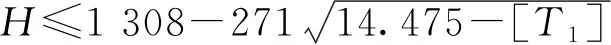
(19)

将表4中的[T1]代入式(19),可进一步获得经典结构动力分析方法所得建筑结构高度建议限值([H])(表5)。

4 建筑结构地震波动响应简化

首先,将高层建筑结构按照基于等效波速和等效波长不变的原则,简化为等效均匀连续直杆介质;然后,通过经典波动理论对等效均匀连续直杆介质的地震响应进行求解;最后,将等效均匀连续直杆介质的加速度、位移、层间变形等具有波动响应特征的结果作为外荷载施加于原建筑结构,采用静力结构分析方法进一步求解原结构的内力响应,从而进行后续结构设计。

表5 经典结构动力分析方法所得建筑结构高度建议限值

该方法的总体流程图如图5所示,具体分析操作步骤如下:

第1步,根据H或T1,复核判断是否需要考虑波动效应。当H≤[H]或T1≤[T1]时,直接采用常规振动分析方法完成后续的分析与设计,否则,按第2步进行后续分析。

第2步,进行常规振动分析,提取建筑结构的质量分布参数、f1、f2等。

第3步，按式(3)计算ce。

第4步，分别按式(6)和(7)估算Ke和λe。

第5步，按式(9)对p0进行解构分析,分离并提取有效的三角脉冲激励分量(pi)。

第6步,采用一维标准波动分析方法求解等效均匀连续直杆介质模型在输入激励分量(pi)下的各项响应指标矩阵ai、di、Δdi,其中,ai、di、Δdi分别为各楼层处不同时刻的加速度、位移以及层间位移矩阵。

第7步，将第6步求解得到的各激励分量(pi)下的响应结果组合叠加,得到p0下的响应结果,如式(20)所示。

(20)

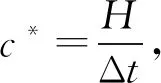
第9步，提取位移响应矩阵d中各时刻tj的层位移列向量dj,施加于常规振动分析模型,求解该时刻结构的内力响应。

第10步，重复第9步,直至输入激励结束。

第11步，提取第10步所得各构件的最大内力和变形进行后续工程设计。

图5 简化的建筑结构波动分析流程图

5 结论

本文总结北京国贸三期主楼、上海中心大厦和深圳平安金融中心超高层建筑振动台模型的试验数据,分析了高层建筑地震波动效应的规律与机制,在试验和理论分析的基础上得到了以下结论:

1)在地表激励作用下高层结构不同层高处的加速度响应存在明显的时滞效应。加速度廓线表现出明显的驻波效应,不同高度处呈现出波腹、波节交替出现的现象。

2)提出了建筑结构的等效波速估算公式,并通过试验数据反分析验证公式的合理性。利用等效波速公式和激励频率得出了等效波长的计算方法。

3)结合结构驻波波腹、波节的计算公式和等效波长,指出建筑的总高度不超过1/4等效波长的情况下,振动分析结果与波动分析结果的趋势一致,并得出了基于质点振动理论的经典结构动力分析方法的两个适用限制条件。

4)提出了一套简化、实用的建筑结构地震波动响应分析方法。首先,该方法按照等效波速和等效波长不变的原则,将高层建筑结构简化为等效均匀连续直杆介质;然后,通过经典波动理论对等效均匀连续直杆介质的地震响应进行求解;最后,将等效均匀连续直杆介质的加速度、位移、层间变形等具有波动效应特征的响应结果作为外荷载施加于原建筑结构,采用静力结构分析方法进一步求解原结构构件的内力响应,从而进行后续工程设计。