负泊松比结构应用于拱结构中的探索

任 鑫,罗钰茗,张相玉,邓洪永,张 毅,周一一,谢亿民

(1.南京工业大学 土木工程学院,江苏 南京 211800;2.常州工学院 土木建筑工程学院,江苏 常州 213002;3.皇家墨尔本理工大学 创新结构与材料中心,澳大利亚 墨尔本 3001)

拱结构(拱形结构)已经广泛应用于工程及日常生活中,工程中诸如拱桥、隧道支撑反拱以及建筑屋顶与造型等;生活中包括拱形门窗、安全帽、鞋子及锅盖等。常见的拱结构类型有三铰拱、两铰拱和无铰拱。由于拱结构能在竖向荷载作用下产生水平推力[1],因此各截面的应力以轴力为主,相比相同跨度的简支梁,拱结构产生的弯矩和剪力较小[2],具有提升结构刚度、节省材料、增大跨度[2]和提高结构抗震性[3]等优点。

泊松比由法国科学家泊松(1781—1840)最先发现并提出。泊松比也称作横向变形系数,数学表达式为横向应变(εx)与纵向应变(εy)比值的负数[4]。泊松比是用于表示材料在单向受力时的横向变形特性。正泊松比材料十分常见,简单来说就是在单向受压(拉)状态下结构发生压胀拉缩的现象[5]。1982年,Frost等[6]首次指出某些具有胞状结构的材料在变形时能够产生负泊松比效应,自此以后,负泊松比材料与结构进入了人们的视野,大量的负泊松比材料与结构相继被发现和创造。近些年来,负泊松比材料和结构被应用到了诸多领域,在医学领域中,负泊松比材料和结构可以用于开发智能食道支架[7]和血管支架[8]等,在生产生活领域,负泊松比材料可用于制作钉子[9]、缓冲头盔[10]等。

负泊松比结构具有特殊的力学性能,如抗剪切性[11-12]、抗压痕性[13-14]、抗断裂强度[15]、曲面同向性[16]、能量吸收性[17]等。罗伟等[18]研究了节点半刚性对木网壳整体稳定性的影响,研究表明采用半刚性节点的木网壳具有稳定承载能力;Easey等[17]对于负泊松比的穹顶形结构已有初步的研究,构建出以正、负泊松比结构为胞元的穹顶结构,并探究这些结构在顶部受压时的力学特性,研究表明以负泊松比结构为胞元的穹顶结构具有优良的抗压痕性与能量吸收性[17]。

拱结构能将结构受到的竖向荷载或面外力转化为轴力[1],本文分别以实心均质拱结构、网格型拱结构、内凹六边形拱结构为研究对象,分析其在水平受压、水平受拉、竖直受压3种受力状态下的拱宽变化,并探究3种拱结构拱宽变化差异的机制。

本文着眼于拱结构在外荷载作用下产生水平轴力的力学特性[19],将平面结构弯起成拱,使负泊松比胞元的排列方向能产生轴力的传递。通过改变结构来改变结构轴力的传递形式,使负泊松比效应得以呈现,巧妙地运用结构力学的知识,以期开拓负泊松比结构在拱结构方面的应用。

1 结构模型及工况介绍

1.1 内凹六边形负泊松比结构特性介绍

本文采用Gibson等[20]在1982年首次提出的内凹六边形胞元,如图1所示。对胞元上下两端施加等值的压力F1,取左侧两斜杆分析,此时左侧两斜杆中存在数值相等的轴力F2,将两斜杆的轴向力分解为水平和竖直两个方向的力Fx、Fy,上下两斜杆竖直方向的分力在中轴处相互抵消而水平分力相互叠加,使得两斜杆交界处即胞元中部向内挤压,斜杆与横杆夹角β减小。当对内凹六边形胞元上下两端施加等值拉力时,两斜杆交界处胞元中部向外伸展。因此,结构整体呈现受压收缩、受拉膨胀的现象。

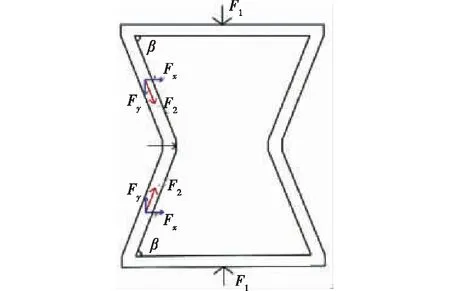
图1 内凹六边形胞元(受压状态)

1.2 拱结构几何构造

图2为3种拱结构及其胞元详图,运用商业软件Rhino进行建模,3种拱结构采用相同的结构尺寸以及结构布置:跨度f=95.40 cm、矢高H=22.83 cm(即矢跨比f/H=0.239 3)、拱宽D=24.83 cm,拱底两端为24.83 cm×1.27 cm×0.30 cm的平台。

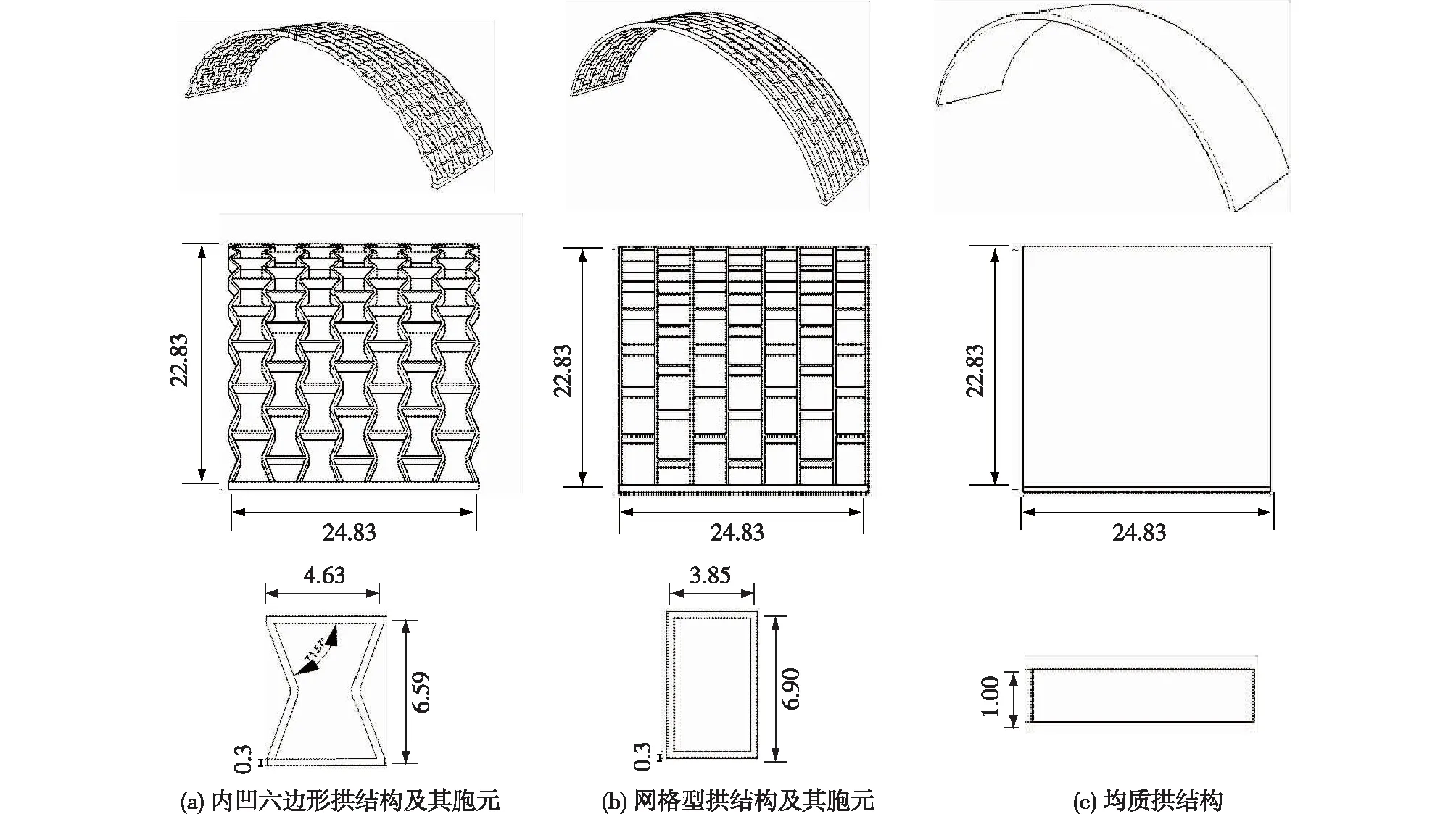
图2 拱结构及其胞元详图(cm)

1.3 有限元分析及3种工况简介

本文用Abaqus6.14.2有限元软件分析结构形变特性。基体材料采用弹塑模型,密度为7.20 g/cm3,弹性模量为616 GPa,泊松比为0.27,网格的初始尺寸为0.50 mm。本文设定拱结构的水平受压、水平受拉、竖直受压3种受力状态,结构形变见图3。

1)水平受压:拱结构的左侧平台铰接,右侧平台在外力推力作用下向左水平推入3.00 mm。在拱结构中选择标记点进行拱宽变化和泊松比研究,标记点在外力作用方向(x方向)上的位移为εx,拱宽变化(y方向)为εy(拱宽增大时,取值为正),则标记点处的泊松比可表示为ν=-εy/εx。

2)水平受拉:拱结构的左侧平台铰接,右侧平台在外力拉力作用下向外水平拉出3.00 mm。标记点处泊松比的计算方法与水平受压状态相同。

3)竖直受压:拱结构的两侧平台铰接,跨中截面处在外力竖直压力作用下跨中下压3.00 mm。标记点在外力作用方向(z方向)上的位移为εz,拱宽变化(y方向)为εy,则标记点处的泊松比可表示为ν=-εy/εz。

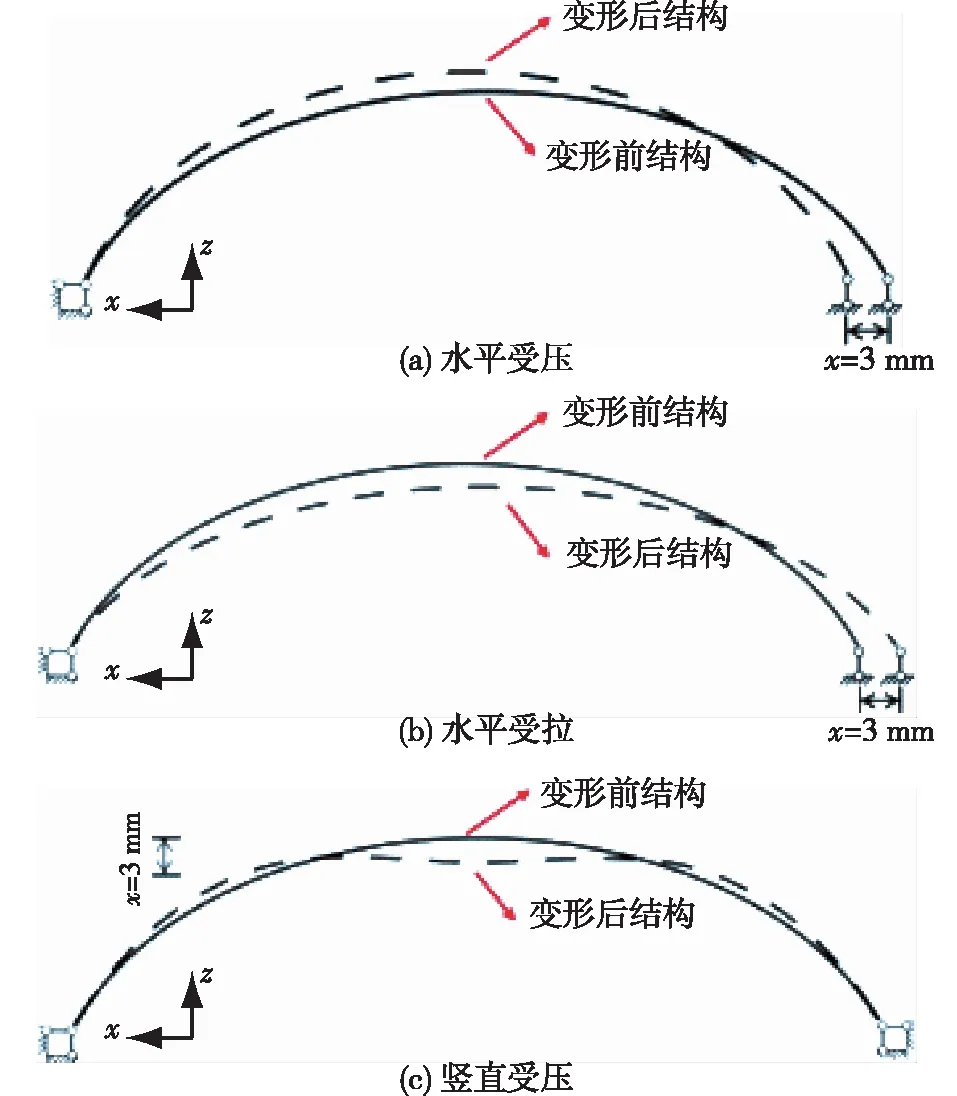
图3 3种受力状态结构形变

2 分析与讨论

以内凹六边形拱结构为例,拱结构中选取3处标记点A、B、C(图4),通过监测标记点处的位置变化表征拱结构的拱宽变化。选取标记点时,标记点A、B、C距离其最近拱底x方向上的距离分别为1/6f、1/2f、1/4f。经Abaqus的模拟分析,标记点A、B、C一定范围的形变特性数据均相近。

图4 内凹六边形拱结构的标记点(cm)

2.1 水平受压状态下的形变表征

图5为实心均质拱结构(简称均质)、网格型拱结构(简称网格)和内凹六边形拱结构(简称内凹)在水平受压时的形变图,图6为3种拱结构在水平受压状态下标记点A、B、C处的拱宽变化和泊松比,由于拱宽变化的数值较小,且不同结构刚度不同,拱结构形变相差较大,因此,拱宽变化和泊松比采用对数坐标。由图5和6可见:在水平受压状态下,实心均质拱结构呈现压胀形变。实心均质拱结构一端受外力推入时,整体结构产生较大的轴力以抵抗外力,其形变特性与平面下的实心均质结构单向受压的形变特性相似。由于正泊松比材料的压胀性,实心均质拱结构整体拱宽增大。拱结构右端水平推入时,实心均质拱结构标记点A、B、C处拱宽增大,且3点处泊松比均为正值,拱宽变化与泊松比正负符号一致,结构形变符合正泊松比材料的形变特性。

图5 3种拱结构水平受压形变图

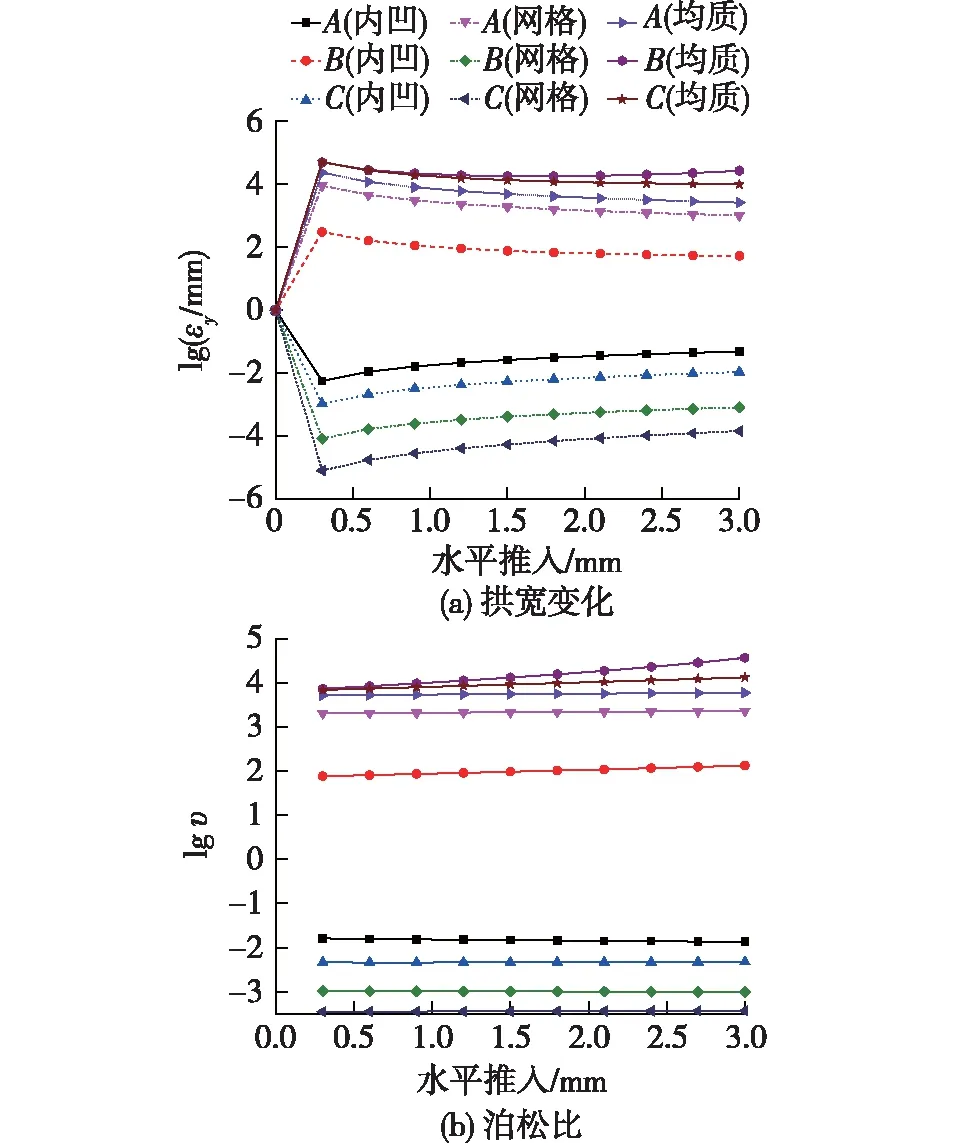
图6 水平受压状态下标记点处拱宽变化和泊松比

由图5和6还可见:在水平受压状态下,网格型拱结构中部呈压缩、两端呈压胀形变。网格型拱结构水平受压时跨中处向外拱起使胞元结构受到拉伸,与平面的网格型结构受拉状态相似,由于正泊松比结构受拉收缩,拱结构跨中区域拱宽减小。拱结构两端受到支座较大的约束作用,结构胞元与平面的网格型结构受压状态相似,拱两端区域拱宽增大。网格型拱结构跨中到两端区域,拱宽呈由减小到增大的变化趋势。由图5和6测得:拱结构右端水平推入时,网格型拱结构标记点A处拱宽增大且泊松比为正值;标记点B、C处拱宽减小且泊松比为负值。可见3点的拱宽变化与泊松比正负符号一致,拱结构AC段符合正泊松比结构的形变特性。

对于内凹六边形拱结构,由图5和6可见:在水平受压状态下,拱结构的中部呈压胀、两端呈压缩形变。内凹六边形拱结构受到水平压力时拱结构向上拱起,由于负泊松比结构具有曲面同向性[16],跨中区域中心的内凹六边形胞元被向外挤出得到伸展,中部区域的拱宽增大。靠近支座处的两端区域受平台约束作用较大,两端区域胞元的形变与内凹六边形胞元受压状态相似,两端区域的拱宽减小。内凹六边形拱结构跨中到两端区域,拱宽呈由增大到减小的变化趋势。由图5和6测得:拱结构右端水平推入时,内凹六边形拱结构标记点A、C处拱宽减小且泊松比为负值;B处拱宽增大且泊松比为正值。可见3点的拱宽变化与泊松比正负符号一致,拱结构AC段符合负泊松比结构的形变特性。

综上可得,与实心均质拱结构和网格型拱结构相比,内凹六边形拱结构在一端水平推入时,跨中区域能体现负泊松比结构的曲面同向性[16],两端区域能体现负泊松比结构的压缩特性。

2.2 水平受拉状态下的形变表征

图7为3种拱结构在水平受拉时的形变图,图8为3种拱结构在水平受拉时标记点处的拱宽变化和泊松比。由图7和8可见:在水平受拉状态下,实心均质拱结构呈现拉缩形变。拱结构产生抵抗外力的轴力(拉力),该轴力在实心均质拱结构上传导,此受力状态下结构的形变与平面实心均质结构受拉状态下形变相似。根据正泊松比材料结构拉缩的特性,实心均质拱结构的整体拱宽减小。拱结构右端水平拉出时,实心均质拱结构标记点A、B、C处拱宽减小,3点处泊松比均为正值,拱宽变化与泊松比正负符号相反,结构形变符合正泊松比材料的形变特性。

图7 3种拱结构水平受拉形变图

图8 水平受拉状态下标记点处拱宽变化和泊松比

由图7和8还可见:在水平受拉状态下,网格型拱结构中部呈拉胀、两端呈拉缩形变。网格型拱结构的一端向外拉出时,拱结构的跨度增大、矢高与跨中区域曲率减小,但网格胞元不会产生曲面同向性[16],胞元间产生了互相的挤压,中部区域拱宽增大。拱结构两端区域受支座约束向外拉出,由于正泊松比结构受拉收缩的形变特征,使两端区域拱宽缩小。网格型拱结构跨中到两端区域,拱宽呈由增大到减小的变化趋势。由图7和8测得:拱结构右端水平拉出时,网格型拱结构标记点A处拱宽减小且泊松比为正值;B、C处拱宽增大且泊松比为负值。可见3点的拱宽变化值与泊松比正负符号相反,拱结构AC段符合正泊松比结构的形变特性。

对于内凹六边形拱结构,由图7和8可见:在水平受拉状态下,内凹六边形拱结构的中部呈拉缩、两端呈拉胀形变。拱顶平面出现了向下凹陷的弧度,由于内凹六边形结构具有曲面同向性[16],拱结构跨中区域拱宽略微减小。拱结构两端的胞元受支座约束向外拉出,由于负泊松比结构拉胀的特性,两端区域的拱宽增大。内凹六边形拱结构跨中到两端区域,拱宽呈由略微减小到增大的变化趋势。由图7和8可见:拱结构右端水平拉出时,内凹六边形拱结构标记点A、C处拱宽增大且泊松比为负值;B处拱宽减小且泊松比为正值。可见3点的拱宽变化与泊松比正负符号相反,拱结构AC段符合负泊松比结构的形变特性。

综上可得,与实心均质拱结构和网格型拱结构相比,内凹六边形拱结构在一端水平拉出时,跨中区域能体现负泊松比结构的曲面同向性[16],两端区域能体现负泊松比结构的拉胀特性。

2.3 竖直受压状态下的形变表征

3种拱结构跨中下压时会产生马鞍形(图3(d))。图9和10为3种拱结构在竖直受压时的形变图和标记点处的拱宽变化及泊松比。由图9和10可见:在竖直受压状态下,实心均质拱结构呈现压缩形变。由于马鞍形的出现,标记点A与标记点B、C在外力方向上产生的位移相反,标记点A处的泊松比为负值。跨中受到向下压力时,拱结构内部的轴力(压力)传递至拱底支座,产生水平推力,在该受力状态下实心均质拱结构的形变与该平面实心均质结构受压形变相似,故拱宽增大。

图9 3种拱结构竖直受压形变图

图10 竖直受压状态下标记点处拱宽变化和泊松比

由图9和10还可见:在竖直受压状态下,网格型拱结构的中部呈压胀、两端呈压缩形变。标记点A位于马鞍形的外拱处,在跨中被向下压低时标记点A由于向外拱起产生与外力方向相反的位移,故标记点A处的泊松比为正值。竖直压力时,中部网格胞元曲率快速减小但网格胞元长度变化较小,因此各个网格胞元结构间产生压胀,网格型拱结构中部拱宽增大;网格型拱结构受竖直压力发生马鞍形外拱形变,外拱处部分网格胞元向外挤出使得胞元结构产生伸展,导致两端拱宽减小。

对于内凹六边形拱结构,由图9和10可见:在竖直受压状态下,内凹六边形拱结构整体呈压缩形变。标记点A位于马鞍形的外拱处,在拱结构整体拱宽减小的情况下标记点A、B、C产生了不同方向的受力位移εz,标记点A处的泊松比为正,标记点B、C处的泊松比为负。3点的拱宽变化与泊松比正负符号相反,拱结构整体符合负泊松比结构的形变特性。

综上可得,与实心均质拱结构和网格型拱结构相比,内凹六边形拱结构在竖直受压时,拱结构整体能体现负泊松比结构的压缩特性。

3 结论

1)实心均质拱结构在受到水平拉(压)力时,拱结构中传递拉(压)力,拱结构整体宽度会发生收缩(膨胀);受到竖直压力时,拱结构截面产生压应力,拱结构整体宽度发生收缩。该现象表明,正泊松比材料的等截面平面结构弯起成拱结构时,其形变特性符合压胀拉缩的形变特点。

2)对网格型拱结构进行分析，当正泊松比胞元结构弯曲形成拱结构,在受水平拉(压)力时,结构整体宽度变化不一致,正泊松比结构压胀拉缩的形变特性不能通过结构整体得到体现,正泊松比效应体现在结构的局部区域。胞元拱结构发生形变时,结构的整体宽度与胞元结构的曲率变化率及截面传递的应力有关。

3)当平面的正/负泊松比胞元结构弯曲成拱结构时,在水平受拉(压)状态下,拱结构整体宽度变化不一致,负泊松比压缩拉胀的特性以及曲面同向性[16]可在结构局部呈现,但不能在结构整体形变中体现。相同受力状态下,正/负泊松比胞元组成的拱结构,拱宽变化未必有整体一致性;结构胞元为正/负泊松比结构时,结构在相近位置或相同区域的形变特性也有所不同,表明拱结构的形变性与组成其胞元的正/负泊松比特性有关。