一种针对高脉冲丢失率的PRI估计方法

王慧娟，苏焕程，张 君，程亦涵

（中国航天科工集团8511研究所，江苏 南京210007）

0 引言

电子侦察系统的作用是截获一定频域和空域范围内的雷达辐射源信号并确定其主要特征参数。信号分选是电子侦察系统的重要组成部分之一[1]，信号分选的正确与否直接关系到电子侦察系统的性能指标。目前的信号分选技术主要包括信号预分选和信号主分选2部分[2]，其中信号预分选主要是根据截获的雷达辐射源脉冲的到达方向（DOA）、载频（RF）等参数进行去交错，降低信号的密度，以便后续的处理；而信号主分选则是在去交错后的脉冲序列基础上实现对雷达辐射源的分选。其中信号主分选的处理流程一般可分为PRI估计和脉冲序列抽取2个部分，即先通过PRI估计得到一个可能的雷达辐射源PRI，再以该可能的PRI作为参考对脉冲序列进行脉冲抽取，根据抽取到的脉冲数量和比例进一步地判别PRI估计的正确与否，从而实现对雷达辐射源的分选。目前的研究重点基本都集中在对雷达辐射源PRI的快速、准确的估计上[3]，这是由于如果不能正确地估计出PRI，则下一步的脉冲抽取将会无法进行，而PRI估计不准确会使后续的脉冲序列抽取出现抽取错误、抽取不彻底以及脉冲断裂等问题，最终导致信号分选失败或者雷达辐射源的特征参数估计不准确。

目前的PRI估计方法都对脉冲的丢失率和脉冲的连续性有一定的要求，如果脉冲丢失率太高就会严重影响对雷达辐射源真实PRI的准确估计。然而，随着新体制雷达技术的应用以及电磁环境越来越复杂，电子侦察系统的截获概率大幅下降，脉冲丢失率非常高，脉冲的连续性被严重破坏，雷达辐射源的PRI特性显著下降，想要正确地估计出PRI变得非常困难，导致信号分选的性能严重下降。

针对传统的PRI估计方法在高脉冲丢失率场景下性能严重下降、很难正确估计出雷达辐射源PRI的问题，本文提出了一种基于带容差的最大公约数法的PRI估计方法，可以在高脉冲丢失率的场景下显著提升PRI估计的正确率，并且可以适应无2个连续脉冲的极端场景。该方法可适用于重频固定、重频参差以及重频组变等重复周期变化相对较为固定的雷达辐射源信号。

1 现有的PRI估计方法

1.1 基于占比统计的方法

基于占比统计的PRI估计方法通过计算脉冲序列的脉冲间隔进行分类统计，搜索其中占比最高且满足一定门限要求的脉冲间隔作为可能的PRI，例如基于统计直方图统计的累积差值直方图法（CDIF）[4]和序列差值直方图法SDIF[5]、PRI聚类法[6]、PRI变换法[7]以及其它相关的改进方法等。实际工程中考虑到脉冲丢失和外界杂乱脉冲干扰的影响，通常会进行多级的脉冲间隔计算。

以统计直方图法为例，通过仿真得到某雷达辐射源发射的脉冲序列以及电子侦察系统实际截获到的脉冲序列如图1所示，图中电子侦察系统实际截获到的脉冲存在一定的丢失率。

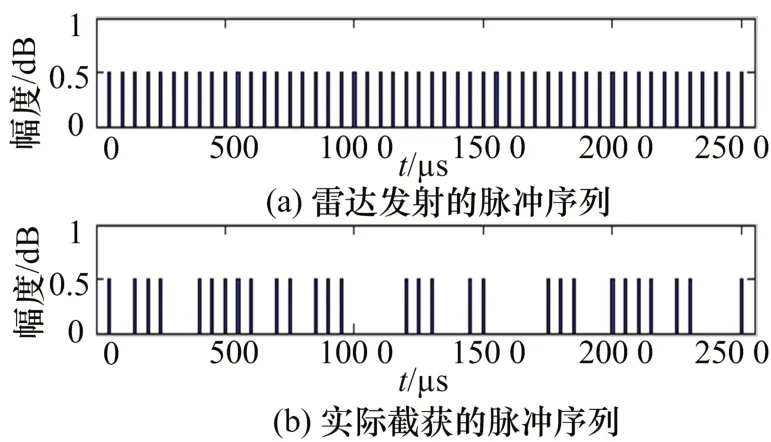
图1 雷达发射和截获脉冲序列示意图

下面对电子侦察系统截获到的脉冲序列进行一级直方图计算，即对接收机接收到脉冲信号中的脉冲到达时间（TOA）参数进行统计分析，将脉冲序列中的各个脉冲的TOA与其前一脉冲的TOA相减，对2个脉冲之间的脉冲间隔进行统计并绘制直方图，将统计值与检测门限进行比较，若统计值高于检测门限，则认为该统计值对应的脉冲间隔为可能的PRI值。脉冲间隔的直方图统计结果如图2所示。

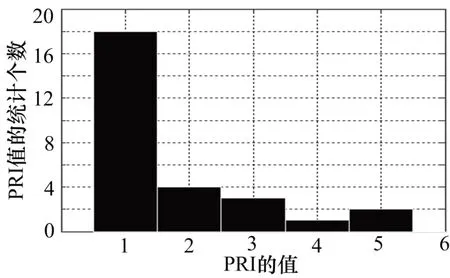
图2 脉冲序列一级直方图示意图

图2中，雷达辐射源的真实PRI对应的脉冲间隔在统计直方图中的峰值明显高于其它脉冲间隔的峰值，故可将其作为估计得到的PRI，这与实际真实结果也是一致的。

通过分析统计直方图的PRI估计过程可知，基于占比统计的PRI估计方法对脉冲丢失率有一定的要求，并且还要求脉冲序列中存在一定数量的连续脉冲，否则真实PRI的峰值高度将无法满足门限要求。

1.2 基于连续特性的方法

基于连续特性的PRI估计方法搜索脉冲序列中脉冲间隔相等的多个连续脉冲（至少3个以上），并以其为基准继续搜索其它脉冲间隔相等（或满足倍数关系）的脉冲，如果搜索到的脉冲数满足门限要求则认为该基准的脉冲间隔为估计得到的PRI，例如直接序列搜索法[8]、动态关联法[9]等。

以直接序列搜索法为例，对脉冲序列进行反复的搜索，直到找到3个脉冲间隔相等的脉冲并将其作为基准，然后继续搜索其它满足相同间隔关系（或倍数关系）的脉冲，其中基准脉冲的数量可根据实际应用需要进行上下调整，如图3所示。

在图3所示的直接序列搜索法中，由于通过基准脉冲能够找到足够多的满足间隔关系的脉冲，故可将基准脉冲的脉冲间隔作为估计得到的PRI，这与实际真实结果也是一致的。

通过分析基准搜索法的PRI估计过程可知，基于连续特性的PRI估计方法对脉冲丢失率的要求相对较低，但是要求脉冲序列中存在多个连续的脉冲，否则无法找到满足要求的基准以开展下一步的抽取。

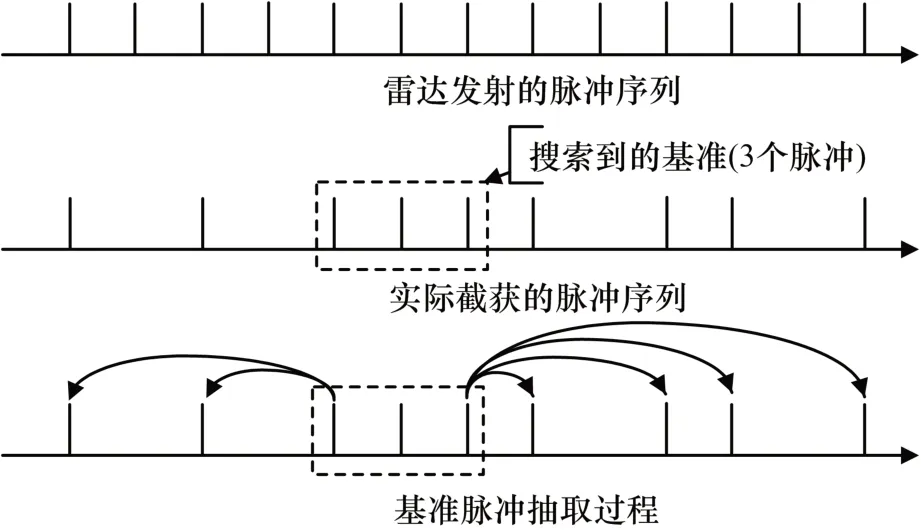
图3 脉冲序列搜索过程示意图

2 改进的PRI估计方法

2.1 方法原理

通过上述的分析，可知现有的PRI估计方法存在的主要不足之处在于对脉冲的丢失率或者脉冲间的连续性有很高的要求，然而在很多应用场景下这2个条件是无法得到满足的。例如在图4的场景中，电子侦察系统截获的脉冲序列的丢失率达到了70%以上，且在整个脉冲序列中不存在2个连续的脉冲，传统的PRI估计方法基本失效。

图4 高脉冲丢失率场景示意图

在图4所示的应用场景中，传统的PRI估计方法无法找出真实PRI的关键原因在于脉冲序列的丢失率太高且缺少2个连续的脉冲，导致既无法统计得到足够高的PRI峰值也无法找到连续的基准脉冲。

虽然由于高丢失率导致计算得到的大部分脉冲间隔都不等于真实PRI，但这些计算得到的脉冲间隔是真实PRI的整数倍，实际上隐含了真实PRI的信息，只是现有的各种PRI估计方法未能够加以有效的提取，从而导致PRI估计的失败。

根据最大公约数定理，真实PRI是多个PRI整数倍脉冲间隔的最大公约数，也就是说通过计算多个脉冲间隔的最大公约数就可以得到真实PRI数值。

以图4所示的雷达辐射源信号为例，计算其一级脉冲序列差并进行等值合并，可得到：

2×PRI、3×PRI、6×PRI、4×PRI、6×PRI、3×PRI、1×PRI、3×PRI、5×PRI、2×PRI、4×PRI。

任意选取几个脉冲间隔并计算它们的最大公约数，其数值即等于真实的PRI数值。

通过上述分析可知，当由于高脉冲丢失率而导致现有的PRI估计方法失效时，可通过计算统计得到的脉冲间隔的最大公约数提取真实的PRI数值，但该方法在实际工程应用中还存在以下2个问题：

1）干扰脉冲的影响：在实际的输入脉冲序列中通常会存在不属于该部雷达辐射源的干扰脉冲，导致计算得到的脉冲间隔并不等于真实PRI的整数倍，将会影响到对最大公约数的计算。

2）测量误差的影响：由于TOA测量误差导致计算得到的脉冲间隔数值并不完全等于PRI的整数倍，而是存在一定范围的测量误差，该误差同样也会导致最大公约数的计算错误。

在实际工程中，通过信号预分选和传统的PRI估计方法先剔除大部分的干扰脉冲，在计算最大公约数时尽可能地选取统计量较多的脉冲间隔，可以较好地解决第1个问题。但是对于第2个问题，由于最大公约数原理的限制以及量化误差导致的测量误差是无法避免的，所以它是影响提取真实的PRI的关键问题。

2.2 最大公约数法

由于传统的最大公约数法[10]对误差非常敏感，不适用于高丢失率下的PRI提取，本节给出一种改进的最大公约数求解方法，该方法的主要优势在于其是一种带容差的最大公约数求解方法，具体方法如下：

对于任意2个正整数A1和A2，求解2者带容差的最大公约数的主要流程如下：

step1：设定门限M和L，其中M是指最大循环次数，L是指误差率门限，对于正整数A1和A2，任意选择其中一个正整数作为高优先级数；

step2：用正整数A1和A2同时除以高优先级对应的正整数，得到商C1和C2；

step3：设定正整数K的初值为0；

step4：将K的数值加1；

step5：如果K等于高优先级数则回到step4；

step6：如果K大于门限M则求解最大公约数失败，结束本流程；

step7：将step2计算得到的商C1和C2乘以K，分别得到乘积KC1和KC2；

step8：分别计算与KC1和KC2最接近的正整数数值KK1和KK2；

step9：分别计算KC1和KK1，KC2和KK2的差值的绝对值KD1和KD2；

step10：如果KD1和KD2不满足同时小于门限KK1×L和KK2×L则回到step4；

step11：用高优先级数除以对应于step8中计算得到的最接近正整数，得到G；

step12：输出A1和A2的最大公约数G。

例如对于2个正整数300和400，显然2者的最大公约数为100，选择与这2个正整数较为接近的另一组正整数302和399，采用传统的最大公约数求解方法显然无法得到数值100，而采用上述带容差的最大公约数可以计算得到这2个正整数之间最为近似的最大公约数100.7。

2.3 方法流程

在上节给出的带容差的最大公约数求解方法的基础上，结合经典的直方图统计法给出基于最大公约数的PRI估计方法，首先给出集合A={A1，A2，…，AN}的M阶最大公约数的定义。

定义：集合A={A1，A2，…，AN}的M阶（2≤M≤N）最大公约数是指：遍历集合A的任意M个元素并计算其带容差的最大公约数，取其计算得到的最大值作为集合A的M阶最大公约数。

在以上定义的基础上，基于最大公约数的PRI估计方法的流程如下：

Step1：采用传统的PRI估计方法对输入脉冲序列进行分选，剔除分选成功的脉冲；

Step2：计算剩余脉冲序列的S阶直方图法，选取峰值最高（即脉冲间隔数最多）的前N个直方形，其对应的PRI数值分别为P1，P2，…，PN，得到集合P={P1，P2，…，PN}；

Step3：设置门限L，并依次分别计算集合P的N，N-1，…，2阶带容差的最大公约数，直到计算得到大于门限L的最大公约数G，否则计算失败并结束本流程；

Step4：将计算得到的最大公约数G作为参考PRI进行下一步的脉冲抽取，如果脉冲抽取成功则将G作为估计得到的PRI输出，否则结束本流程。

在上述流程中，将参数S和N设置得较高有利于提高PRI估计正确的概率，但是会消耗更多的计算资源、存储资源和时间资源，因此在实际工程中应当进行综合的考虑。而门限L应当设置为高于电子侦察系统能够适应的最小PRI或者已知可能出现的最小PRI，以剔除明显不正确的PRI数值。

采用基于最大公约数的PRI估计方法在电子侦察系统截获的脉冲丢失率较高、脉冲间的连续性被严重破坏的场景下，能够有效提高PRI估计的成功率。同时该方法首先需要完成传统的PRI估计，可以看作是对现有PRI估计方法的补充，并且计算过程较为简单，有很高的工程应用价值。

3 仿真验证结果

为了验证本文中提出的PRI估计方法在高脉冲丢失率场景下的有效性，下面对传统的统计直方图法、直接序列搜索法以及本文所提出的PRI估计方法进行对比仿真验证。

仿真场景：使用Matlab仿真10部PRI固定的雷达信号源，并设置随机脉冲丢失率范围为0%～95%。在不同的脉冲丢失率下进行仿真，共运行1 000次计算平均值，3种方法在不同脉冲丢失率下的分选正确率（分选正确率=（正确分选的脉冲数/总的雷达脉冲数×100%））如图5所示。

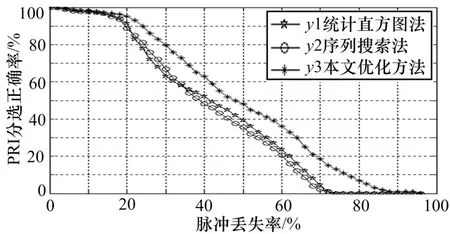
图5 脉冲丢失率对PRI分选正确率的影响

从图5的仿真结果可以看出，在脉冲丢失率小于20%时，3种方法的PRI估计正确率基本接近；而当脉冲丢失率大于20%后，本文提出的方法明显比传统的统计直方图法和序列搜索法有着更高的正确率，在脉冲丢失率在[20%70%]之间时，本文提出的优化方法的正确率同比提升最大达到16%，当脉冲丢失率大于70%后，传统的PRI估计方法由于很难找到2个连续的脉冲而基本失效，而本文提出的PRI估计方法仍然能够保证一定的正确率。

4 结束语

本文提出了一种基于带容差的最大公约数法的PRI估计方法，相比较于传统的PRI估计方法，该方法对脉冲丢失率的要求相对较低，且不要求脉冲序列中必须存在2个连续的脉冲，在高脉冲丢失率的应用场景下有着明显的优势。同时，本文提出的PRI估计方法可作为现有方法的补充，额外占用的计算和存储的资源很少，有很高的工程应用价值。