因果影响与函数式依赖：从逻辑的视角分析

谢凯博

1 引言

变量间相互依存的关系是自然科学、社会科学与哲学研究中的重要内容。变量之间的联系是普遍的，同时也是多样的，判断变量之间的联系具有怎样的性质在实践当中具有重要意义。例如，当在科学研究中观察到行为X与疾病Y之间存在着联系（例如X与Y常常相伴而生），但在实践当中，我们会不仅仅满足于X与Y之间“存在联系”或“不存在联系”这样的判断，还需要把握这种联系更深层次的性质，例如：这种联系是否依赖于X和Y以外的其他变量，还是X单独决定了Y；X和Y的联系是否是一种因果联系？如果忽视这样的问题就无法将这种联系应用于实践，例如我们不能从行为X与Y的联系推出要增加X还是减少X的结论，因为X与Y的联系未必是一种因果联系，X对Y也许根本不存在因果影响，是一个其他变量Z共同影响X和Y建立起了X和Y表面上的联系，而这种表面上的联系反而在实践当中具有欺骗性。因此许多学科，尤其是计算机、哲学研究，都试图建构处理变量之间联系的理论，尤其是关于因果联系的理论。

这些理论当中的部分理论（例如[7]）侧重于通过概率来研究变量间的联系。它们在人工智能领域获得了大量的应用。但近年来在人工智能领域也涌现出一批从结构方程的角度进行因果研究的理论。结构方程是一种直接表征因果规律的函数，同时也能够表达反事实结构。相比于概率角度的研究，基于结构方程的因果模型更容易从逻辑学的角度进行研究，其中[9,11,12]等将人工智能领域的因果理论应用到了逻辑当中，提出以因果模型为语义基础的经典因果逻辑。

而另一方面，在逻辑学当中也诞生了从其他方面探讨变量间联系的逻辑。例如[1]的函数式依赖逻辑（Logic Functional Dependence，以下简称LFD 逻辑）通过函数式依赖这一概念研究变量间的决定关系。

本文首先将对这些已有成果进行介绍，并分析因果逻辑与函数式依赖逻辑这两个系统之间的区别。同时，为了进一步探讨两种路径之间的联系，本文将基于[5]的成果对因果模型进行认知方面的扩充，从而使我们能够从认知的角度发掘两者之间的联系。

2 基于结构方程的因果关系

Pearl，Galles 以及Halpern 提出了经典的因果模型来刻画变量间的因果关联。（[8,9,12]）因果模型通过变元来描述模型所要刻画的基本事实，并通过结构方程刻画变量之间影响的方式。值得注意的是，尽管Pearl，Galles 以及Halpern 所提出的因果模型在思想上是相似的，但在具体的定义方式上仍有许多细节上的差异（即便在同一作者的不同的文章中，对因果模型的定义方式也有所差异），因此出于简洁考虑本文不再进行分别介绍，而是在符号使用和定义的具体方式上结合了[10]与[6]中对因果模型的形式化表述。我们对于因果模型的形式化定义如下：

定义2.1(因果模型).一个因果模型是一个三元组〈S,F,A〉，其中：

·S=〈U,V,R〉是该模型的变元字符集（signature），U={U1,...,Um}是外部变元（指不受其他变元影响的变元）的有穷集合,V={V1,...,Vn}是内部变元（指受其他变元影响的变元）的有穷集合。函数R是变元的取值范围，对于U ∪V中的每个变元X,R(X)是X这个变元可取的值的集合。

·F={FVj |Vj ∈V}是结构方程的集合。其中对于每个Vj ∈V，FVj ∈F被称为关于Vj的结构方程，是从对Vj外所有变元的所有可能的赋值到R(Vj)的映射：若a是对Vj以外所有变元的赋值1即a 的定义域为U ∪V {Vj}。，则(a)是R(Vj)中的一个值。

·A是对变元的全局赋值函数2因果模型的赋值部分在不同的文献中表述方式有所差别。关于因果模型的经典定义中，如[9]以及[10]中的定义，因果模型的赋值只需要通过外部变元的赋值来表征。而在其他一些文献中，如[6]则通过全部变元的赋值来表征。本文采取后一种表征方式，原因是这种表征方式更方便我们将因果模型与函数依赖模型进行比较。，对于U ∪V中的每个变元X，A(X)∈R(X)是A对X的赋值。若A是一个对变元X1,...,Xn的赋值函数，且A(X1)=x1,...,A(Xn)=xn，可将A记作(X1=x1,...,Xn=xn)，而当X1,...,Xn

在上下文中明确时，它也可被简写为(x1,...,xn)。在因果模型中，全局赋值函数A必须与结构方程F相符合，即对于任何Xj ∈V，必有

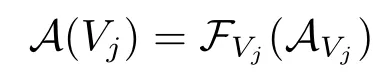
其中AVj是A中的对Vj以外所有变元的赋值3即对任意X ∈U ∪V {Vj}，有AVj(X)= A(X)。。

S定义了一个因果模型所需要考虑的所有变元的名称及其取值范围

F用以表示在所有可能的情形下，Vj这个变元在其他变元影响下所应具有的值。值得注意的是，在一些关于因果模型的论述中（如[6,12]），关于一个变元的结构方程并不是以所有该变元以外的变元取值方式为定义域，而是以某几个其他变元的取值方式为定义域。但这种定义方式与定义2.1所给出的定义方式并不冲突，因为只有某些变元（而非全部变元）决定一个变元取值的情况也可以看成是所有其他变元共同决定一个变元取值的特殊情况。

在一个因果模型〈S,F,A〉中，结构方程组F描述了变元之间的因果关系。我们由此可以定义一个变量对另一个变量的因果影响。

定义2.2(因果影响).若F是一个关于内部变元集V的结构方程集。对于V中的每个变元Vj，不妨设变元分别为U1,...,Um,V1,...,Vj-1,Vj+1,...,Vn,为X1,...,Xm+n-1。

给定结构方程集F，我们称一个变元Xi对一个与之不同的内部变元Vj具有直接因果影响，记作Xi →F Vj，当且仅当：存在多元组

许多文献中对因果模型的一个重要假设是，因果模型中无循环的因果影响。无循环的因果影响可以通过+关系来定义：我们称一个因果模型〈S,F,A〉是无循环的，当且仅当对于S中任意两个变元X与Y，如果，则。本文中所提及的因果模型，我们都预设无循环的因果影响。

在[9]所提出的基于因果模型的形式化路径中，干预是用以刻画因果推理的核心概念。干预是对模型中变量的强制调整。一个在模型M上将X的值设置为x的干预可以看作是一个将原模型M映射到干预后的模型MX=x的算子。经过干预后的新模型MX=x与原有模型M的差别是新模型MX=x中关于X这个变量的结构方程（即FX）被替换为一个输出始终为x的常函数（即对于任意赋值a，。可将这一概念从对单个变元的干预推广到到对一组变元的干预，其一般定义如下：

4如前文所述，我们预设因果模型M不包含循环的因果影响。易证当F不包含循环的因果影响时，也不包含循环的因果影响。而对于不包含循环的因果影响的结构方程集必有唯一解。因此我们可以保证(i)(ii)(iii)所得到的赋值函数是唯一的。

公式X⇝Z的直观含义是“X对Z具有直接的因果影响”，它表达了存在一组对U ∪V{X,V}中这些变元赋值的,使得在这种赋值的基础上，将X的值从x1变动到x2（其中x1与x2不同），根据结构方程将使Z的值由z1变动到z2（其中z1与z2不同）。

3 函数式依赖逻辑

函数式依赖逻辑是在[1]中提出的关于变量之间的决定关系的逻辑。其模型由一系列的变量以及对变量赋值的集合构成。

变量之间的决定关系是生活中常见而且重要的一种关系，我们可以通过如下例子来说明什么是变量间的决定关系：

例1.假设鱼肉是否被烤熟取决于放在烤箱中加热的时间，在烤箱电源接入的情况下烤箱加热的时间由人在机器上预设的时间决定，如果不接电源则烤箱不运转。简便起见，我们假设鱼只有熟与不熟两种状态，时间只有0 分钟，5 分钟，10 分钟，15 分钟这四档，只有当加热不少于10 分钟时鱼才熟。我们可以用下面这个表格来列举所有可能的情形：

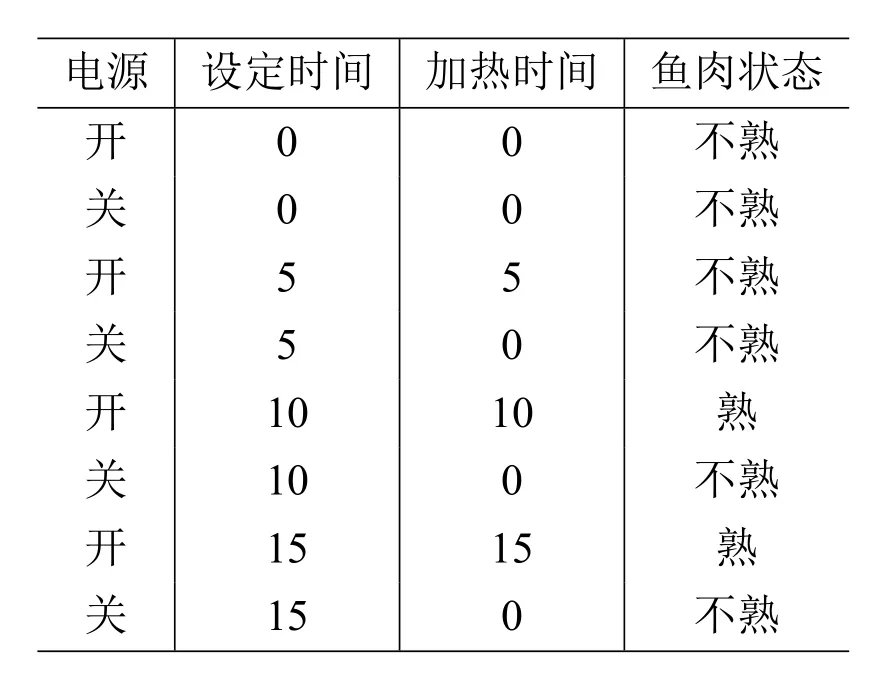
表1:对烤箱加热中各变量间关系的直观刻画

从直观上看，设定时间和电源状态决定了鱼肉的状态，但反之，鱼肉的状态并不决定设定时间和电源的状态。而这种直观在表格上所反映出来的是如果表格中任意两行设定时间和电源的状态都是相同的，那么这些行中所对应鱼肉的状态就必定相同的。但反之，鱼肉的状态相同的行所对应的设定时间和电源状态不一定相同。

这样一个表格可以看作是一个关于变量实际可能情形的集合，即变量所有取值组合的子集。它能够通过“如果确定了某些变量的值，则可确定另一些变量的值”的方式反映变量之间的决定关系。

LFD 逻辑所基于的函数式依赖模型就是以这种方式刻画的变量间的数值。

定义3.1.一个（关于变量集V的）函数式依赖模型M 是一个二元组(M,A)，其中M=(O,I)是一个一阶关系模型（O为一阶模型的论域而I是一阶模型的解释函数），而A ⊂OV是可取变量赋值的集合（对于任意s ∈A，x ∈V我们称s(x)∈O为变量赋值s 对x 所赋的值或在s 上x 的值）

LFD 逻辑的语言中包含两种用以表达函数式依赖的算子D与D，分别表达一组变元对一个变元值的决定关系以及一组变元对一个命题真假的决定关系。

定义3.2(LFD 的语言).LFD 语言中的公式φ的递归定义如下

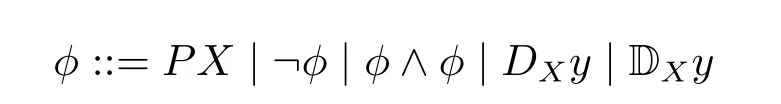
给定函数式依赖模型M=(M,A)，我们称在s上变元集X决定变元y（或称变元y依赖于变元集X），记作s |=DXy，当且仅当对于任意t ∈A，若对任意x ∈X,s(x)=t(x)成立，则s(y)=t(y)；我们称在s上，变元集X决定了命题φ（命题φ依赖于变元集X），记作s|=DXφ，当且仅当对任意t ∈A，若对任意x ∈X,s(x)=t(x)成立，则t|=φ。

烤箱加热的例子可以被形式化为一个包含四个变元的函数式依赖模型M（电源、设定时间、加热时间、鱼肉状态可以看成是四个变量），在这个模型中，可取变元赋值的集合A就是表1所列的所有组合的集合。假设在s这个状态上，电源=关，设定时间=加热时间=0，鱼肉状态=不熟，那么根据对函数式依赖算子的定义，{电源,设定时间}这个变元集决定了鱼肉状态，写作s|=D{电源,设定时间}鱼肉状态。但反之，根据函数式依赖算子所在公式的真之条件，{鱼肉状态}这个单元集既不决定电源这个变元，也不决定设定时间这个变元。这和我们直观上对这个例子中变量间决定关系的理解是一致的。

4 因果模型与函数式依赖模型的比较

因果模型与函数式依赖模型都刻画了变量间的相关性。例如在烤箱的例子当中，我们不仅可以用函数式依赖关系来刻画电源、设定时间、加热时间、鱼肉状态四者之间的关系，我们也可以通过建立因果模型来描述这些变量间的相关性：

如果我们为烤箱的例子建立相应的因果模型〈S,F,A〉，那么S中包含“电源”、“设定时间”、“加热时间”、“鱼肉状态”这四个变元，其中“加热时间”、“鱼肉状态”为内部变元。F={F加热时间,F鱼肉状态}。其中F加热时间可以被表达为：如果电源的状态为开，则加热时间的值与设定时间的值相同，如果电源状态为关，则加热时间的值为0；F鱼肉状态可以表达为，鱼肉状态为“熟”当且仅当加热时间等于10 或15。F加热时间与F鱼肉状态共同描述了这个例子中变量间的相互影响。并且不难验证，同时符合F加热时间与F鱼肉状态的所有赋值正是表格1中所列举的值。

本章将着重比较两种路径的异同。

4.1 因果模型与函数式依赖模型的对应

我们看到，例1所对应的因果模型为〈S,F,A〉，它所对应的函数式依赖模型M=(M,A)中A等同于所有与F相符合的对S中变元赋值的集合。更一般地，一个因果模型描述了变量所必须遵循的因果规律，而所有满足这些因果规律的情形反映出了变量之间相互依赖的关系。所以很自然地，我们可以将后者看作是这个因果模型所对应的函数式依赖模型：

定义4.1.我们称一个以V为变元的函数式依赖模型M=(M,A)（其中M=(O,I)）是因果模型C=〈S,F,A〉（其中S=〈U,V,R〉）所对应的函数式依赖模型当且仅当：V=U ∪V,∪X∈U∪V R(X)⊆O，且对任意a ∈A及任意X ∈U ∪V有a(X)∈R(X)，且A中有且仅有与F相符合的对S中变元的赋值。

通过因果模型与函数式依赖模型的对应关系，我们可以对在前者基础上定义的因果影响，与在后者基础上定义的函数式依赖关系进行比较。

4.2 因果影响与函数式依赖的区别与联系

因果模型中所定义的因果影响与LFD 所定义的函数式依赖都是对变量相关性的描述，但是两者之间并不等同。因果模型中的因果影响刻画了变量之间的“因果上的相关性”，而函数式依赖刻画了变量之间“观察上的相关性”。所谓观察上的相关性指的是变量在观察结果上所呈现出来的相关性。例如若A 和B 两个事件要么同时发生，要么同时不发生时，则他们之间存在一种观察上的联系：若观察到A 发生或不发生，则B 的发生与否就是确定的。这种相关性可以是因果的，比如:

例2.地面结冰导致地很滑。所以当观察到地面结冰时，“滑”这个变量的值就是确定的。

但不具有因果关系的变量之间也可以呈现出观察上的相关性。这种相关性可能来源于认知上的“证据”，例如：

例3.一起案件中有甲乙两个嫌疑人。其他人都有不在场证明。所以若甲是清白的，那么乙就确实作案了。

在这个例子中，甲作案与否和乙作案与否并没有因果关系（“甲清白”和“乙作案”的联系并不是源于甲的清白会导致乙作案），而是因为其他人的不在场证据才建立了这种联系。

这种差异体现为：一个变量与另一个变量满足函数式依赖的条件并不意味着前者对后者具有直接因果影响。例如考虑以下例子：

例4.在一个因果模型中仅有A和B两个变量，其中A是外部变元而B是内部变元。结构方程FB的定义方式是FB(a)=x当且仅当a(A)=x。

显然在这个例子中对于任意与FB相符合的赋值，A与B的赋值必定相同。因此在与该因果模型对应的函数式依赖模型中，满足LFD 中对函数式依赖算子D{B}A的定义（即A依赖于变元B,或称变元B本地决定变元A）。然而由于A是外部变元，将FB替换为任意常函数都无法使A的值发生变化，B对A不具有因果影响。

正如[12] 所强调的，“观察上的相关性”并不等同于“因果的相关性”。在例4中，A对B的因果影响在观察上体现为“A与B的值总是相同”这一变量间的相关性，但是仅“A与B的值总是相同”这一性质出发不足以区分到底是A在因果上影响了B还是B在因果上影响了A。

但另一方面，正如“观察上的相关性”与“因果的相关性”是相互关联的（例如虽然不能从观察上的相关性推出因果的相关性,但如果两个变元存在因果影响则这种影响往往在观察上体现为某种相关性），函数式依赖关系和因果影响虽不可等同，却仍具有紧密关联。例如函数式相关与因果影响满足以下性质：

该性质直观上反映了，任何一个变元都被其因果母节点的集合（所有对该变元具有因果影响的变元的集合）所决定。

5 对因果模型的认知扩展

如前一章所述因果上的相关性与观察上的相关性既有联系又有区别。因果模型只反映了变元之间因果上的相关性，以及由因果相关性所带来的观察上的相关性，但不能反映由因果以外的因素带来的观察上的相关性。

因此我们将对因果模型进行扩展，使之能够表征认知上的相关性。借鉴认知逻辑中对不确定性的处理，不确定性可以通过可能世界的集合进行刻画（[2-4]）。在因果模型中一个可能世界可以视为一组对全部变量的赋值，因此我们可以以一个变元赋值的集合来刻画因果模型中变元值的不确定性。例如一个因果模型中有两个变元X1与X2两个变元，其中R(X1)=R(X2)={1,2}。我们可以用T={(1,1),(2,1)}这个集合来表达对X1,X2的真实赋值是(1,1)还是(2,1)的不确定性（与经典因果模型中的书写方式一样我们将一个把X1赋为1，X2赋为2 的赋值简写为(x1,x2)这样一个二元组），这样T就表达了对X2为1 的确定性以及对X1值的不确定性。

因此我们将认知因果模型由二元组(S,F)扩展为一个三元组(S,F,T)。我们采用[5]中的定义：

定义5.1(认知因果模型).一个认知因果模型是一个三元组〈S,F,T〉，其中S=〈U,V,R〉是变元字符集,F是关于V的（不包含循环的因果影响的）结构方程集，T是关于U ∪V的赋值函数的非空集合，且T中的每个变元赋值都与F相符合。

将经典的因果模型扩展为认知因果模型后，相应地，我们也可以定义认知因果模型上的干预：

在将因果模型进行认知角度扩展的同时，我们也对其语言做相应的扩展。在经典的因果语言的基础上，我们加入了用以表达知识的“K”算子和用以表达信息更新的“!”算子。Kφ表达了认知主体知道φ成立，而[ψ!]φ表达了在观察到ψ这一事实之后，φ这个命题成立。

同时[5]证明了因果模型的认知扩展能够被公理化，并提供了其完全性证明。

6 认知因果模型与函数式依赖的关系

当我们将因果模型进行了认知扩充之后，我们可以基于定义4.1得到一个认知因果模型与函数式依赖模型的对应关系。

定义6.1.我们称一个以V为变元的函数式依赖模型M=(M,A)（其中M=(O,I)）是认知因果模型〈S,F,T〉所对应的函数式依赖模型当且仅当：V=U ∪V,R(X)⊆O，且A=T。

由此我们可以将因果模型与函数式依赖模型进行比较。但需要注意的是，函数式依赖模型并不依赖变元字符集是有穷的，即变元的数目与变元取值范围可以是无穷的。而在因果模型中，变元字符集必须是有穷的，因此当我们比较一个因果模型与函数式依赖模型时，都只能在变元字符集有穷的范围内进行。

[1]指出，函数式依赖也可以从认知角度进行理解，所谓“一个变元Y被一个变元集合S所决定”也可以理解为：只要获知S中变元的任意取值，就能知道Y这个变元的值。

也就是说，当我们预设变元的数量及取值范围有穷时，我们能将LFD 中带有函数式依赖算子的公式翻译为LPAKC中的公式。

7 结论

在本文中，我们介绍了因果模型、函数式依赖模型，并分析了基于因果模型所定义的因果影响与基于函数式依赖模型定义的变量间决定关系的差异与联系：因果影响不等于函数式依赖关系，后者只反映了变量之间在观察上的相关性；但同时我们证明了基于因果模型上的因果影响关系，任意变量因果母节点的集合与该变量都存在函数式依赖关系。

为了从认知层面进一步比较因果关系与函数式依赖关系，本文介绍[5]对因果模型进行认知扩展的工作，从而在认知层面找到因果模型的路径与函数式依赖模型的路径的联系。这种联系在逻辑上体现为当预设变量的数目与取值范围为有穷时，存在LFD 语言LPAKC（对因果逻辑的语言进行认知扩展后的语言）之间的对应关系。当然两种路径之间的联系并不仅限于本文所讨论的这些方面，有待于未来进一步的探索。同时本文对两种路径的比较局限于变元有穷这一范围内（而函数式依赖模型本身并不预设有穷变元），而对于无穷变元情况下的讨论仍然有待研究。