Coverage and Area Spectral Efficiency Analysis of Dense Terahertz Networks in Finite Region

Minwei Shi,Xiaozheng Gao,Anqi Meng,Dusit Niyato

1 School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China

2 School of Cyberspace Science and Technology,Beijing Institute of Technology,Beijing 100081,China

3 Engineering Center of Digital Audio and Video,Communication University of China,Beijing 100024,China

4 School of Computer Science and Engineering,Nanyang Technological University,Singapore 639798

Abstract:This paper develops a general and tractable framework for the finite-sized downlink terahertz(THz)network.Specifically,the molecular absorption loss,receiver locations,directional antennas,and dynamic blockage are taken into account.Using the tools from stochastic geometry,the exact expressions of the blind probability,signal-to-interference-plus-noise ratio(SINR)coverage probability,and area spectral efficiency(ASE)for the reference receivers and random receivers are derived.The upper bounds of the SINR coverage probability are also obtained by using the generalized dominant interferers approach.Numerical results validate the accuracy of our theoretical analysis and suggest that two or more dominant interferers are required to provide sufficiently tight approximations for the SINR coverage probability.We also show that densifying the finite terahertz networks over a certain density threshold will degrade the coverage probability while the ASE keeps increasing.Moreover,deploying more obstructions appropriately in ultra-dense THz networks will benefit both the coverage probability and ASE.

Keywords:terahertz;interference;area spectral efficiency;densification;stochastic geometry

I.INTRODUCTION

Terahertz(THz)communication,operated between 0.1 THz and 10 THz,is envisioned as one of the potential technologies for 6G to enable hundreds of gigabit per second data rates due to its large available spectrum resources[1-3].Nonetheless,THz transmissions incur high propagation loss stemming from the molecular absorption of water vapor molecules,thus significantly limiting the communication distance[4-6].Therefore,the densely deployed THz access points(APs)will be a promising scheme to meet the rapidly increasing traffic demand for the indoor communication scenario[7].

In terms of dense THz networks,interference and coverage are critical factors affecting the network performance.In recent years,stochastic geometry has emerged as a unified mathematical tool to analyze the coverage performance of wireless networks in various frequency bands[8,9].By modeling the THz APs as a homogeneous Poisson point process(PPP),the authors in[10]investigated the signalto-interference-plus-noise ratio(SINR)performance of terahertz wireless local area networks incorporating the indoor blockage effects caused by the walls and human bodies,based on which the expressions of approximated coverage probability were derived.To address the reliability degradation caused by selfblockage and dynamic human blockage in THz communication systems,[11]evaluated the performance achieved by multi-connectivity strategies.In addition,the impacts of APs’heights on the uplink and downlink coverage performance of 3D THz networks were highlighted in[12]and[13],respectively.The authors in[14]derived the coverage probability and ASE of unmanned aerial vehicular(UAV)-aided THz networks under the assumptions of HPPP-distributed UAVs and users.This model was further extended in[15]by operating small cells with wireless backhaul capability.Moreover,the downlink interference and coverage probability of integrated THz and radio frequency network was investigated in[16]under biased average received power association strategy.

However,due to the severe reflection loss and indoor blockage effects in the THz band,the existing fading models in the microwave and mmWave bands are not applicable in the THz band,and thus the coverage analysis is still an unsolved issue[10].Based on this consideration,most of the stochastic geometry-based studies resort to evaluate the moments of interference[17,18]or bounds of coverage[13],rather than the exact expression of coverage probability.The authors in[19]derived the mean and variance of SINR by using the Taylor expansion approximation of SINR.The cumulative distribution function(cdf)of interference was fitted by the log-logistic distribution in[20]with the help of the parameter estimation techniques.Similar method was applied in[17],which approximated the cdf of interference to the modified log-normal distribution.Moreover,the authors in[13]derived the upper bounds of the downlink SINR coverage probability in three-dimensional environment by applying the dominant interferer analysis.

In this paper,the downlink coverage and area spectral efficiency(ASE)of the dense THz networks in finite region are investigated.Specifically,we model the locations of THz APs as a finite homogeneous PPP(FHPPP).The directional beamforming and blockage as well as molecular absorption loss are incorporated to characterize the distinguish propagation features of THz.Different from[20,21],the presented system model accounts for the finite THz network.Under this framework,it allows to evaluate the performance of the central users and edge users separately,which is essential since these two kinds of users are with different interference exclusion regions.When compared to[17,18],which focus on the mean and variance of SINR,the proposed framework obtains exact expressions of the blind probability as well as the cdfof SINR,thus providing more detailed informations about the coverage of the finite THz networks.Besides,it also derives the close-formed upper bounds and lower bounds of the coverage probability by invoking the generalized dominant interferers approach.Simulation results validate our theoretical analysis and give several design insights of the finite-sized dense THz networks.

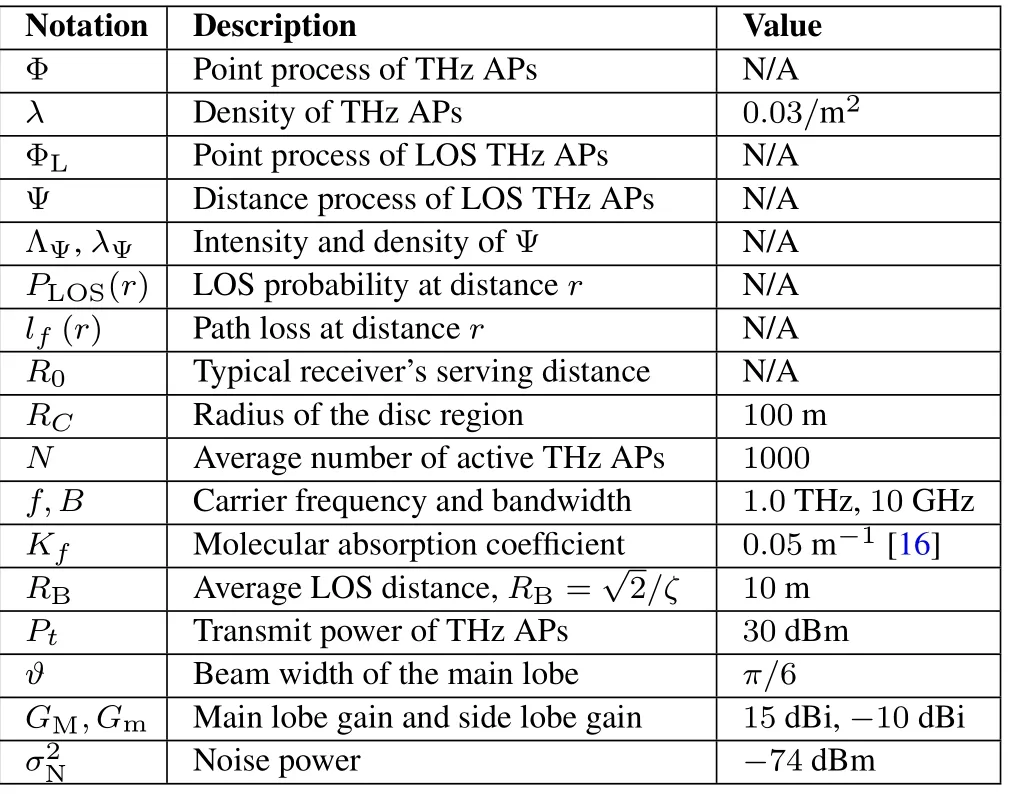
Table 1.Descriptions and typical values of parameters.

The rest of the paper is organized as follows.The system model is detailed in Section II.Then,Section III focuses on the calculations of the blind probability and the distribution of the serving link with respect to the reference receiver.In Section IV,we derive the exact expression of SINR coverage probability,followed by its upper bounds and lower bounds by using theK-dominant interferers approach and Markov inequality,respectively.Finally,Section VI concludes the paper.

II.SYSTEM MODEL

In this section,we first introduce the network layout of the finite-sized THz network,and then describe the blockage and propagation models.The notations and descriptions of parameters are summarized in Table 1.

2.1 Network Layout

Figure 1.Illustration of finite THz cellular network.

This work considers the downlink of THz cellular networks in finite region as depicted in Figure 1,where the THz APs Φ are uniformly and independently deployed in the circle regionB(O,RC)following a FHPPP[22]with intensityλband transmit powerPt,whereOdenotes the center of the circle,andRCis the radius.Therefore,the average number of THz APs inB(O,RC)is given byN=πλR2C.In addition,we assume the active receiver density scales with the AP density,and thus the THz network is fully loaded.Without loss of generality,we conduct our analysis on a typical receiver,which is located at the origino[23].

2.2 Blockage

Recent research has suggested that the obstructions such as human body can cause significant loss in THz frequency band and thus result in non-lineof-sight(NLOS)transmission[10].In this paper,we assume exponential line-of-sight(LOS)probabilityPLOS(r)=e-ζr,whereris the distance between the transmitter and the receiver,andζis the blockage parameter determined by the average size and the deployment density of the blockers[24].With the probabilistic blockage model,the LOS THz APs seen from the typical receiver are denoted by ΦL≜{x:x∈Φ,x→ois a LOS link},which is an independent thinning of Φ with retention probabilityPLOS(r).

2.3 Propagation Model

Due to the high molecular absorption in THz frequency band,the LOS transmissions are more dominant than the NLOS transmissions.Therefore,we neglect NLOS links in this paper.Since the frequencyselective THz channel suffers from the free-space path loss as well as the molecular absorption,we model the total path loss of the LOS THz link with distanceras[4,6]

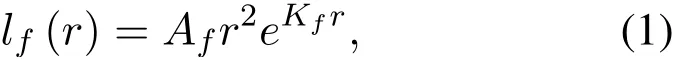
whereAf=(4πf/c)2,cis the speed of light,andKfis the frequency-dependent molecular absorption loss coefficient at frequencyf.

To compensate for the high path loss at THz frequency band,directional beamforming is adopted at THz APs to enhance the intended signal[25-27].For simplicity,the sectored antenna model is applied to model the antenna arrays[16].Specifically,the directional beamforming gain is expressed as

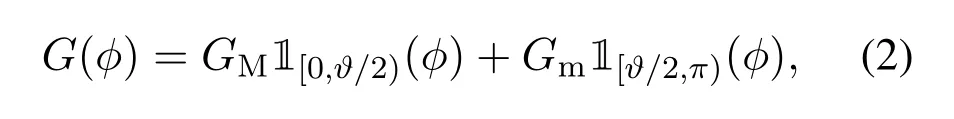
whereφ∈[-π,π)is the angle off the boresight,GMis the main lobe gain,Gmis the side lobe gain,ϑis the beamwidth of the main lobe,and 1(·)is the indicator function.The THz APs are assumed to adjust their antenna steering orientation toward its intended receiver through beam alignment techniques.Consequently,the effective antenna gain of an interfering THz APs is a discrete random variable beingGMwith probabilityϑ/(2π)and beingGmwith probability 1-ϑ/(2π).

Regarding the access strategy,we assume that the typical receiver is associated with the nearest LOS AP x*.Therefore,the serving distanceR0≜‖x*‖is equal to inf{Ψ}.And the downlink SINR can be determined by

where

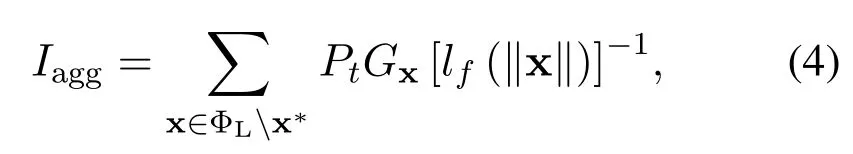
andis the thermal noise power.

III.DISTANCE DISTRIBUTION

In this section,we derive the expressions of the blind probability and the distribution of the serving distance,which are served as the foundations of the coverage analysis in the next section.

3.1 Distance Process

Since the signal and interference powers are subjected to the distances between the THz APs and the typical receiver only,it will be useful to map ΦLto its distance process Ψ≜{‖x‖:x∈ΦL}.The following Lemma characterizes the intensity of Ψ.

Lemma 1(Distance Process of THz-LOS links).Conditioned on the typical receiver located at distance V from the origin,Ψis a PPP with intensity measure and intensity given by

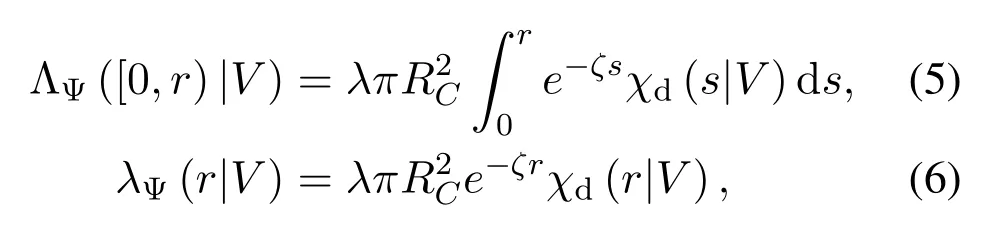
respectively,where r∈[0,RC+V],and

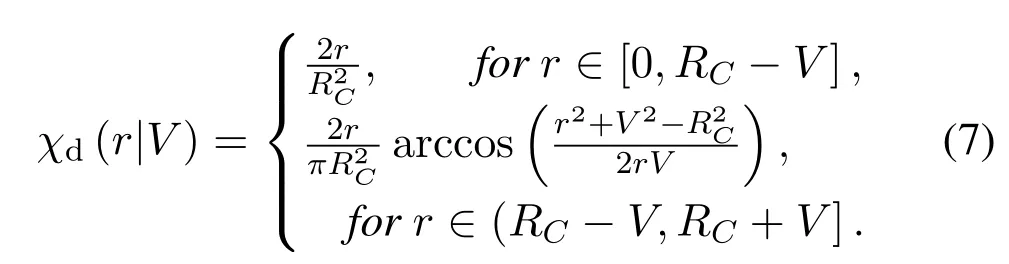
Proof.Letf:x→‖x‖be a measurable function.Since it holds that ΛΨ(f-1{r})=0,∀r∈R+,wheref-1{r}is the preimage of the set{r},the proof is completed by invoking the mapping theorem of PPPs[23,Theorem 3.4.3].

Remark 1.Specifically,for the central receiver(V=0),since χd(r|0)=(5)and(6)reduce to

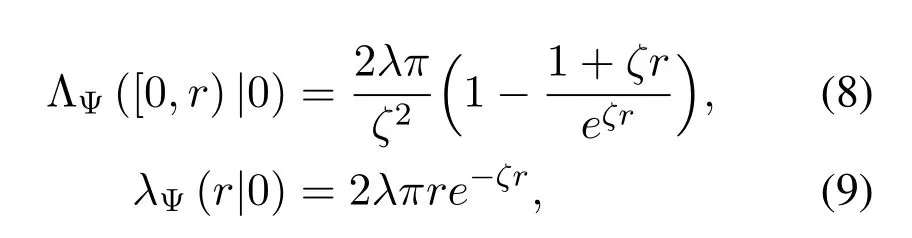
respectively,where r∈[0,RC].

3.2 Serving Distance

Due to the impacts of blockage and AP density,some receivers may have no opportunities to be served by the LOS APs,i.e.,ΦL=Ø.The percentage of such kind of receivers is termed as blind probability in this paper,which is characterized in the following Lemma.

Lemma 2(Blind Probability).The blind probability of the reference receiver located at distance V fromthe center is

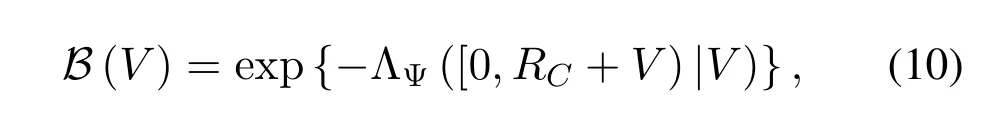
where V∈[0,RC],andΛΨ(·)is available in(5).

Proof.The proof follows from the void probability of PPPs[28,Theorem 1.1.5].

Remark 2.The blind probability of overall users can be obtained by averaging(10)over V as=

Lemma 3(Distance Distribution of the Serving Link).

The cdf and probability density function(pdf)of the distance from the typical receiver to its serving AP are

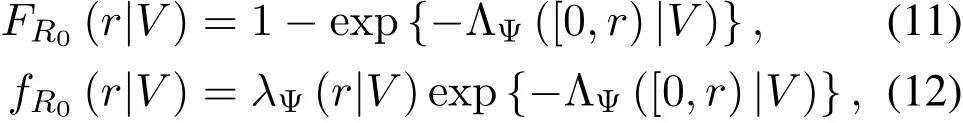
respectively,where r∈[0,RC+V].

Proof.The proof follows from the void probability of PPPs[28,Theorem 1.1.5].

Remark 3.Specifically,for the central receiver,(11)and(12)reduce to

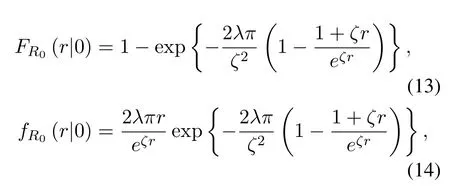
respectively,where r∈[0,RC].

IV.COVERAGE AND ASE ANALYSIS

In this section,the SINR coverage probability and ASE are extensively analyzed based on stochastic geometry.For ease of understanding,the relations between the lemmas,theorems,and corollaries in this section are illustrated in Figure 2.

4.1 SINR Coverage Analysis:Exact Results

To investigate the location-dependent performance,we will evaluate the SINR coverage probability of the reference receiver,denoted asCref(θ|V),whereθis the SINR threshold andVis the distance from the reference receiver to the center.According to(3),Cref(θ|V)can be formulated by

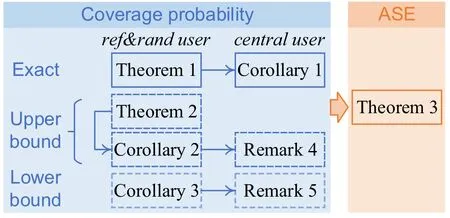
Figure 2.Logic flow diagram of analysis.

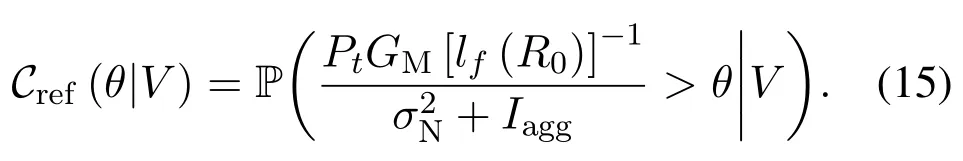
The following Theorem presents the exact expression ofCref(θ|V).

Theorem 1(SINR Coverage Probability).The SINR coverage probability of the reference receiver located at distance V from the center is given by

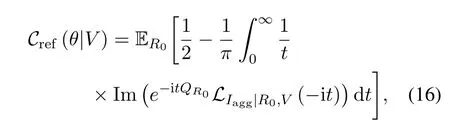
where θ is the SINR threshold,and

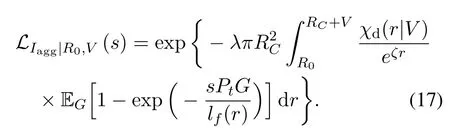
And the coverage probability of the random receiver is

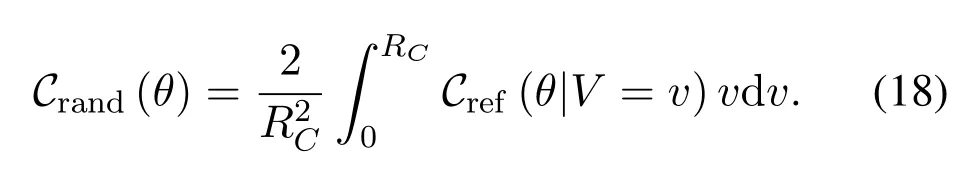
Proof.From(15),we have

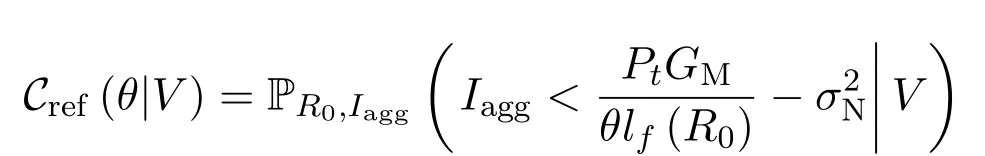
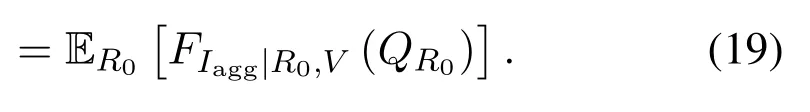
Then,by invoking the Gil-Pelaez theorem[29],FIagg|R0,V(·)can be calculated as

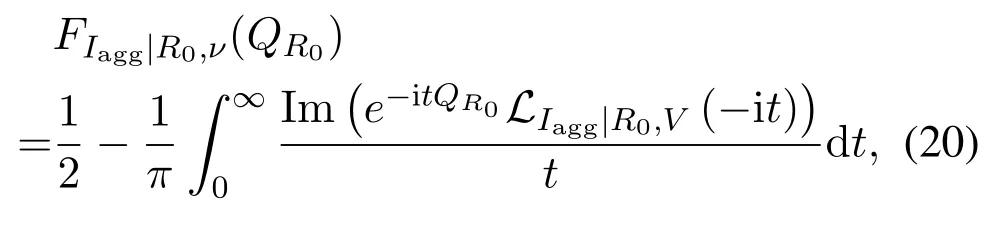
whereLIagg|R0,V(·)denotes the Laplace transform ofIaggconditioned onR0andV.Let Ψo≜Ψ{R0},and then we have

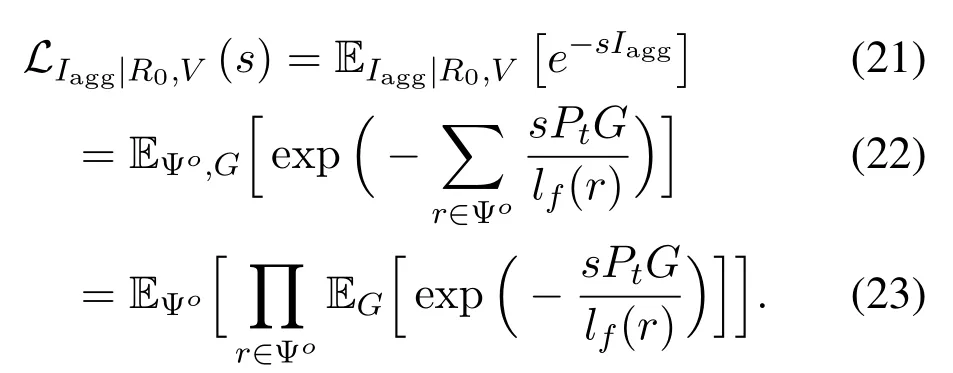
From the Slivnyak’s theorem,Ψois still a PPP.By using the probability generating functional(pgfl)of PPP[30,Example 4.2],(23)can be rewritten as

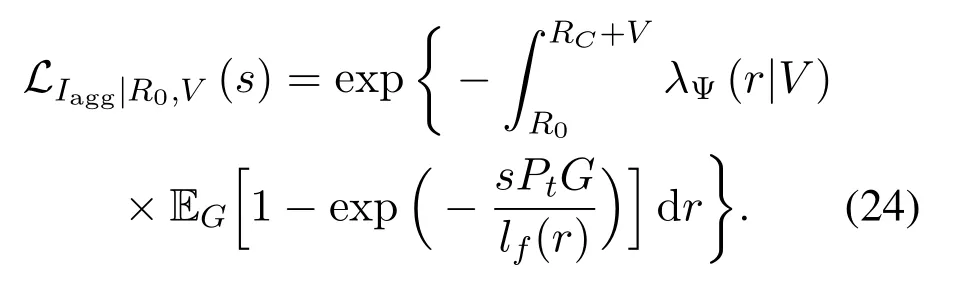
Finally,substituting(6)into(24)completes the proof.

Corollary 1(SINR Coverage Probability).The SINR coverage probability of the central receiver is given by(16),where

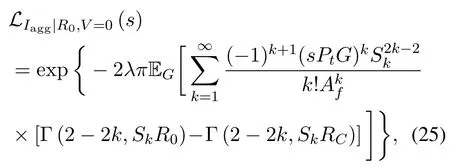
and Sk=ζ+kKf.

Proof.First,substituting(9)into(24)gives

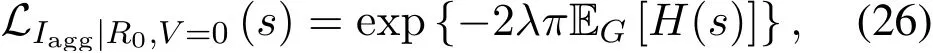
where

Then,invoking the Taylor expansion of exponential function,we have

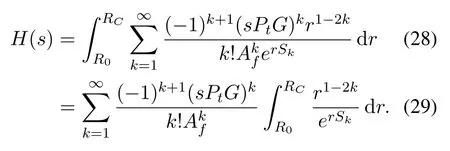
Finally,the proof is completed by employing the substitutiont←rSkand using the definition of the upper incomplete gamma function.

4.2 SINR Coverage Analysis:Upper Bounds

In this subsection,we give the upper bound of SINR coverage probability by using theK-dominant interferers approach,which can be treated as the generalization of the 1-dominant interferer approach in[13],to provide tighter bounds for ultra-dense THz networks.

For ease of notation,we define the set of LOS THz APs with main-lobe to the typical receiver as ΨM,i.e.,ΨM≜{‖x‖:x∈ΦL,Gx=GM}.Apparently,ΨMis an independent thinning of Ψ with retention probabilityThe upper bounds ofCref(θ|V)is given in the following Theorem.

Theorem 2(K-Dominant Approach).Denoting W(·)as the Lambert W-function andΨM(A)as the number of elements ofΨMthat fall in A,the SINR coverage probability of the reference located at distance V from the center is upper bounded by

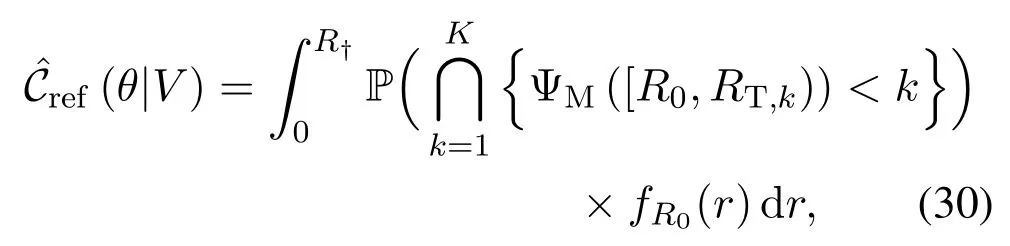
where K∈Z+,and

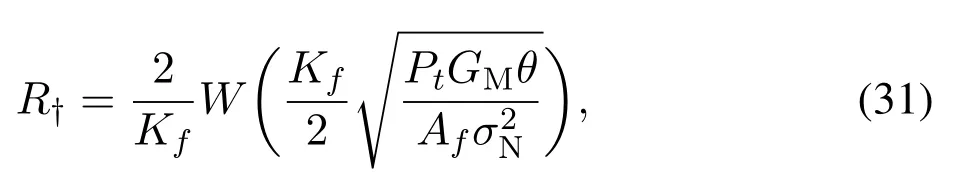
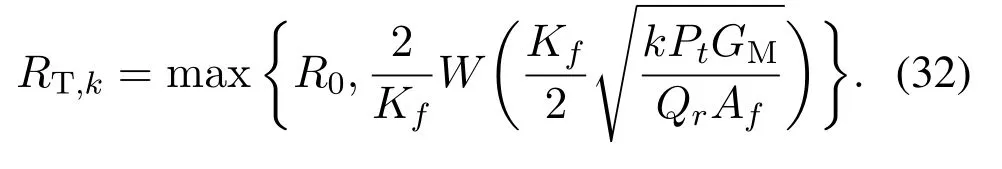
Proof.The basic idea of theK-dominant interferers approach stems from the fact that the number of THz APs located in thek-vulnerability region should be no more thankTHz APs to meet the requirements coverage,wherek∈Z+andk＜K.First,solving the equationyields

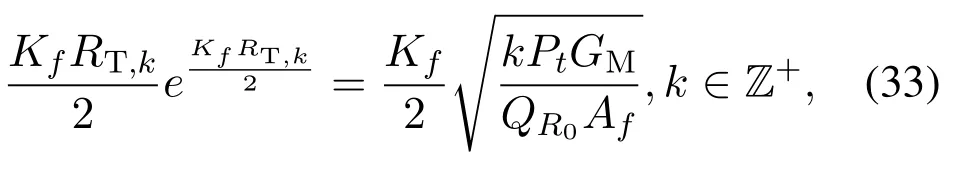
which gives the solution(32).Then,conditioned onR0andV,denote by Ekthe event ΨM([0,RT,k))＜kand by C the eventIagg＜QR0.It is apparent that the events Ekare the necessary conditions of the typical receiver being in coverage,i.e.,Ek⊃C,and thusTherefore,Cref(θ|V,R0)can be formulated as

Finally,by averaging the right-hand side of(35)over the serving distanceR0,we complete the proof.

Since the events Ekin the proof of Theorem 2 are not independent with each other,the direct calculation of(30)for largeKseems infeasible.Nevertheless,we present the easy-to-use approximations withK=1 andK=2 in the following Corollary.

Corollary 2(K=1,2).By using the 1-and 2-dominant interferers approaches,the SINR coverage probabilities of the reference receiver located at the distance V from center are upper bounded by

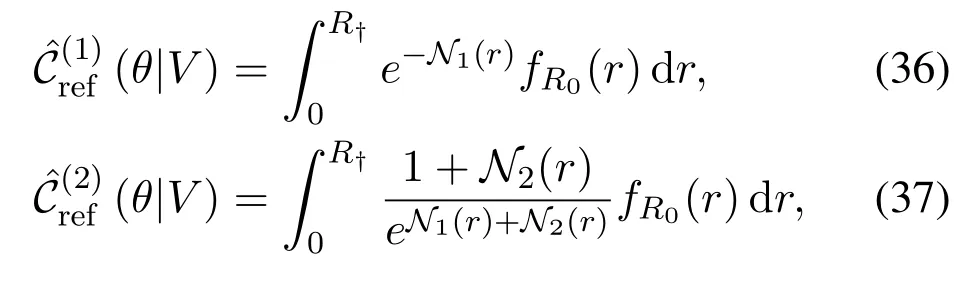
respectively,where

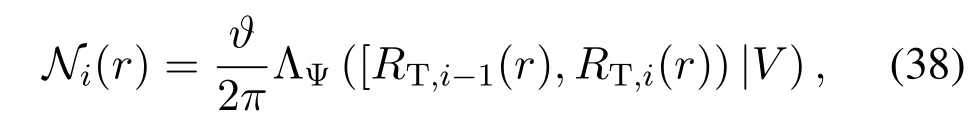
where i∈{1,2},R†and RT,k(r)are available in(31)and(32),respectively.

Proof.The results forK=1 is straightforward from Theorem 2 and is hence skipped.ForK=2,conditioned on the serving distancer,it is apparent that

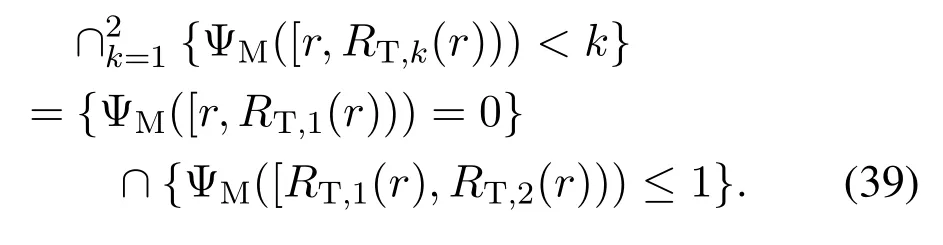
Since ΨM([r,RT,1(r)))and ΨM([RT,1(r),RT,2(r)))are two independent Poisson random variables with mean valuesN1(r)andN2(r),respectively,(37)is obtained by using the probability mass function of Poisson distribution.

Remark 4.Regarding the central receiver,(38)reduces to

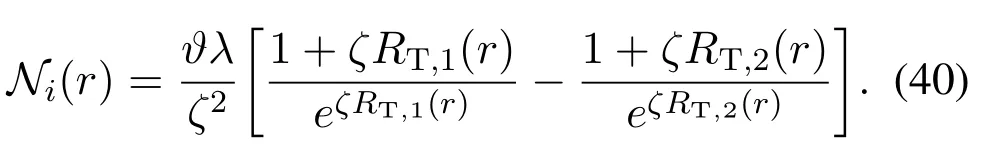
4.3 SINR Coverage Analysis:Lower Bounds

By leveraging the Markov inequality,the lower bounds ofCref(θ|V)andCrand(θ|V)are presented in the following Corollary.

Corollary 3(Markov Lower Bound).The SINR coverage probabilities of the reference receiver and random receiver are lower bounded by

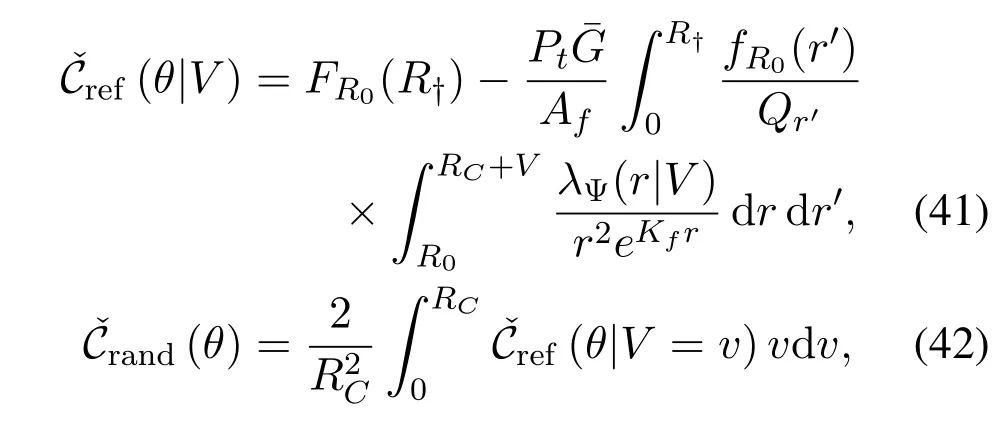
respectively,where

Proof.From the Markov inequality,we have

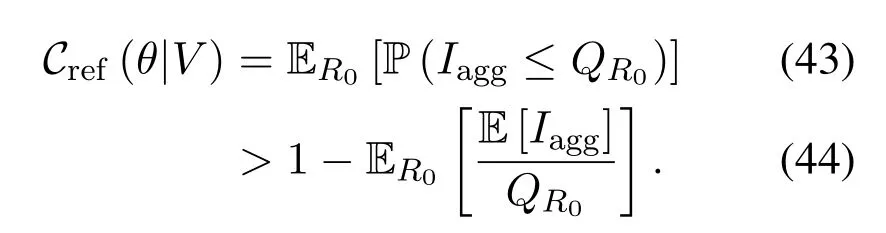
According to the Campbell theorem of PPP[30,Theorem 4.1],the mean value ofIaggis determined by

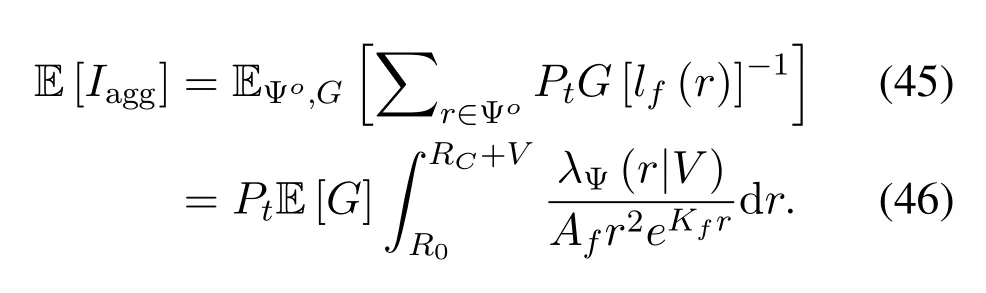
Finally,substituting(46)into(44)completes the proof.

Remark 5.From Corollary 3,by substituting(9)into(41),the SINR coverage probability of the central receiver is lower bounded by

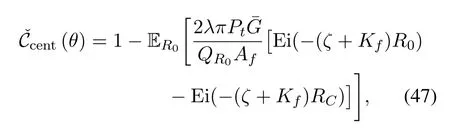
whereEi(·)is the exponential integral.

4.4 ASE

The ASEE(θ)evaluates the total data rate in a unit area normalized by the bandwidth and is measured in[bps/Hz/m2][31].Given the SINR thresholdθ,E(θ)is expressed as

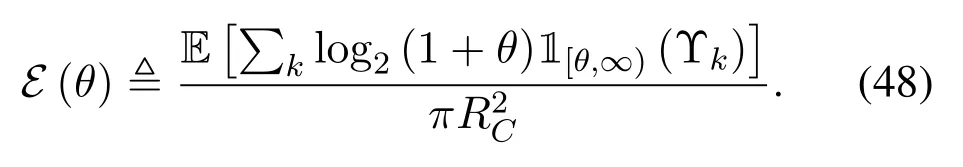
Recalling the expression(18),we formulate the ASE in the following Theorem.

Theorem 3(ASE).The ASE for the finite THz networks is given by

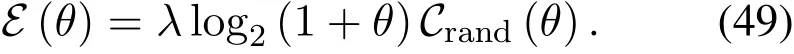
Proof.The proof is straightforward and is thus omitted here.

Remark 6.Note that Theorem 3 presents the relations between Crand(θ)and E(θ).Therefore,the upper bounds and lower bounds of ASE can be determined by applying Theorem 2 and Corollary 3,respectively.

Figure 3.Blind probability as a function of average LOS distance for central receivers and edge receivers.

V.SIMULATION RESULTS

In this section,we present numerical results of the performance metrics involved in Sections III and IV in finite THz networks,and investigate the effects of system parameters on the network performance.The main parameters and default values employed in simulations are summarized in Table 1 unless stated otherwise.

5.1 Validations of the Analytical Result s

Figure 3 shows the blind probabilityBof central users and edge users versus the average LOS distanceRB.It can be seen that the analytical results match accurately with the simulation results,which validates the accuracy of Lemma 2.As expected,the blind probability monotonically decreases with respect to the average LOS distanceRB.The reason is straightforward:a largerRBimplies that more THz APs could provide LOS transmissions to the given user.In addition,the area of the vulnerability region for the central users is larger than that for the edge user,which results in lower blind probability for the central users.Moreover,it shows that the network densification indeed degrades the blind probabilities for both kinds of users.This trend can be explained by the two facts that:1)deploying more THz APs provides more association opportunities for the users;2)the decreased average distances between the THz APs and users due to the network densification benefit the LOS probability.

Figure 4.SINR coverage probability versus threshold θ for central user and edge user when RC=50 m and N=500.

To investigate the accuracy of the theoretical results of the SINR coverage probability in Section IV,we compare them with the numerical results under different thresholdθin Figure 4.It is observed that both of the exact expression and the upper bound provide excellent matches with the numerical results,demonstrating the accuracy of Theorem 1 and Corollary 2 for the considered THz communication system.In addition,we also highlight that,with the increase of SINR thresholdθ,the vulnerability region[RT,0,RT,1]shrinks,and the difference between the exact result of coverage probability and its 1-dominant upper bound increases slightly.This observation indicates that the upper bounds with more dominant interferers are needed to provide sufficiently tight approximations.

5.2 The Impact of THz Features

Directional transmission and sensitivity to molecular absorption are two key features of THz communication.Figure 5 presents the coverage probability versus SINR thresholdθwith various molecular absorption coefficientsKfand main lobe gainsGM.It can be observed that increasing the main lobe gain of the THz APs improves the SINR coverage probability.The reason is that larger antenna gain can significantly improve the received power of the serving signal,while the total power of interference and thermal noise do not proportionally increase with the main lobe gain.Additionally,another observation is that a largerKfleads to smaller coverage probability.This is due to the fact that larger path loss diminishes the strength of both the serving and interfering THz signals,while the noise power remains unchanged.Besides,we also find that increasing the SINR threshold has a diminishing effect on the difference between the coverage results under various molecular absorption coefficients.

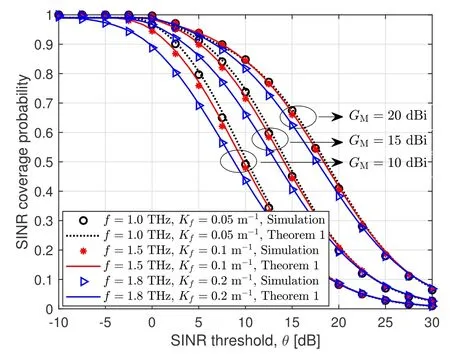
Figure 5.SINR coverage probability versus threshold θ when RC=100 m and N=1000.

5.3 The Impact of Densification

In Figure 6,we evaluate how the THz AP density influences the network performance in terms of coverage probability and ASE with various thresholdsθand blockage parametersζ.From Figure 6a,we can observe that for a given configuration,the coverage probability first increases with the THz AP density because more THz APs lead to shorter communication distance and higher LOS probability for the users.Then,whenNis sufficiently large(e.g.,N＞125 forθ=10 dB andthe THz network becomes interference-limited,after which the coverage performance starts decreasing.Comparing the SINR coverage probabilities with different thresholdsθ,it can be found thatθhas a marginal effect on the turning points of coverage probability,while the coverage performance with higher threshold degrades faster than that with lower threshold.In addition,by comparing the SINR coverage probabilities with various blockage parametersζ,we highlight that when the THz APs are sparsely deployed(e.g.,N＜30),the environment with less blockages has better coverage performance.With more THz APs deployed in the network,the coverage probability in severe blockage environment outperforms that in light blockage environment.The reason is that for ultra-dense THz networks,severer blockage will obstruct more interference while keeping the serving signal strength in a desired threshold.This observation also indicates that appropriately introducing more blockages in ultra-dense THz networks will benefit the coverage probability.

Figure 6.Network performance as a function of average number of APs with various threshold θ and blockage parameter ζ when RC=30 m.

Figure 6b demonstrates the impact of densifying the the THz APs on the network ASE.It is observed that the ASE monotonically increases withNregardless of the decline of SINR coverage probability(as seen from Figure 6a)when the THz APs keep densifying(e.g.,N＞125).This trend indicates that the densification gain counteracts the enlarged interference in dense THz networks.

VI.CONCLUSIONS

In this paper,we examine the coverage probability and ASE in ultra-dense finite THz networks.Specifically,we model the THz APs and receivers in a circle region and incorporate the impacts of molecular absorption,receiver location,dynamic blockage,and directional beamforming.Numerical results demonstrate the accuracy of our analysis.We can learn that compared with the edge users,the central users are more likely to be served by the LOS THz transmitters with higher coverage probability.For instance,the blind probability of edge users is 22%higher than that of central users when the average LOS distance is 15 m.Moreover,the optimal density of THz APs to maximize the coverage probability whenθ=10 dB is around 0.053 APs/m2,at which the coverage probability is 78% and the ASE is 0.13 bps/Hz/m2.However,deploying more APs will degrade the coverage performance while the ASE performance keeps increasing.In addition,introducing more blockages appropriately in ultra-dense THz networks will benefit the coverage probability and ASE.

In the future,we aim to incorporate the ray-tracing based channel model,which considers the reflection and scattering of THz signals,to evaluate the performance of THz networks more realistically.In addition,more advanced and sophisticated beamforming and association techniques are postponed for future work.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China(No.61771054).