Wideband Channel Estimation for THz Massive MIMO

Jingbo Tan,Linglong Dai*

Beijing National Research Center for Information Science and Technology(BNRist)as well as the Department of Electronic Engineering,Tsinghua University,Beijing 100084,China

Abstract:Terahertz(THz)communication is considered to be a promising technology for future 6G network.To overcome the severe attenuation and relieve the high power consumption,massive multipleinput multiple-output(MIMO)with hybrid precoding has been widely considered for THz communication.However,accurate wideband channel estimation,which is essential for hybrid precoding,is challenging in THz massive MIMO systems.The existing wideband channel estimation schemes based on the ideal assumption of common sparse channel support will suffer from a severe performance loss due to the beam split effect.In this paper,we propose a beam split pattern detection based channel estimation scheme to realize reliable wideband channel estimation in THz massive MIMO systems.Specifically,a comprehensive analysis on the angle-domain sparse structure of the wideband channel is provided by considering the beam split effect.Based on the analysis,we define a series of index sets called as beam split patterns,which are proved to have a one-to-one match to different physical channel directions.Inspired by this one-to-one match,we propose to estimate the physical channel direction by exploiting beam split patterns at first.Then,the sparse channel supports at different subcarriers can be obtained by utilizing a support detection window.This support detection window is generated by expanding the beam split pattern which is determined by the obtained physical channel direction.The above estimation procedure will be repeated path by path until all path components are estimated.Finally,the wideband channel can be recovered by calculating the elements on the total sparse channel support at all subcarriers.The proposed scheme exploits the wideband channel property implied by the beam split effect,i.e.,beam split pattern,which can significantly improve the channel estimation accuracy.Simulation results show that the proposed scheme is able to achieve higher accuracy than existing schemes.

Keywords:THz communication;massive MIMO;hybrid precoding;beam split;wideband channel estimation

I.INTRODUCTION

Terahertz(THz)communication has been considered as one of the promising techniques for future 6G network,since it can provide tenfold bandwidth increase and thus support ultra-high transmission rate[1-5].To overcome the severe attenuation in the THz band(i.e.,0.1-10 THz[1]),massive multiple-input multipleoutput(MIMO),which can generate directional beams by a large-scale antenna array,is essential for THz communication[4].However,the traditional fullydigital structure,where each antenna is connected to one radio-frequency(RF)chain,will introduce very high power consumption[6].To solve this problem,hybrid precoding structure can be used for THz communication[7-9],where the high-dimensional precoder is decomposed into a high-dimensional analog beamformer(usually realized by analog components[10])and a low-dimensional digital precoder(usually realized by a reduced number of RF chains).Thanks to the sparsity of THz channels,it has been proved that hybrid precoding is able to achieve the near-optimal achievable rate performance[7-9].

1.1 Prior Works

To design an efficient hybrid precoder,the highdimensional channel is essential at the base station(BS).However,channel estimation is challenging in massive MIMO systems with hybrid precoding structure[11].Specifically,since the number of RF chains is much smaller than the number of antennas in the hybrid precoding structure,the BS cannot obtain signals at each antenna element simultaneously.As a result,to obtain sufficient observation to accurately estimate the high-dimensional channel,the channel estimation overhead of conventional channel estimation scheme,e.g.,least square(LS)scheme,will be unacceptable when the number of antennas is very large[12].

To deal with this problem,exploiting channel sparsity with the help of compressive sensing algorithms for channel estimation has been widely investigated to realize low-overhead channel estimation in massive MIMO systems[13-20].For example,a distributed compressive sensing based multi-user channel estimation scheme was proposed in[13],where the joint angle-domain channel sparsity among different users was utilized.[14]proposed an orthogonal matching pursuit(OMP)based channel estimation scheme for massive MIMO systems with hybrid precoding structure by using the angle-domain channel sparsity.Besides,a joint channel estimation and tracking scheme was also proposed based on the framework of compressive sensing in[15].In addition,the channel estimation problem in lens-array based massive MIMO with a simple antenna switching network is investigated in[16],where a redundant dictionary and the corresponding compressive sensing based scheme are proposed.

However,these schemes in[13-16]were designed for narrowband systems.Although these narrowband schemes can be extended in wideband systems,carrying out narrowband schemes subcarrier by subcarrier will result in high complexity due to a large number of subcarriers,especially in wideband THz massive MIMO systems.To realize efficient wideband channel estimation,wideband channel estimation schemes have been proposed for millimeter-wave massive MIMO systems[18,19].In particular,[18]proposed a simultaneous orthogonal matching pursuit(SOMP)based scheme,where channels at different subcarriers were jointly estimated based on the assumption of common sparse channel support(i.e.,the sparse channel supports at different subcarriers are the same).Besides,an OMP based wideband channel estimation scheme was proposed in[19],where the sparse channel supports at some subcarriers were independently estimated using the classical OMP algorithm,and then the wideband channel was recovered based on the common sparse channel support created by the already obtained sparse channel supports.Furthermore,[20]proposed a close-loop sparse channel estimation solution for multi-user massive MIMO systems.Unfortunately,the ideal assumption of common sparse channel support in the above two schemes is not practical for THz systems due to the beam split effect[21].Specifically,the beam split effect can be seen as a serious situation of the widely known beam squint[22].It means because of the wide bandwidth and a large number of antennas in THz massive MIMO systems,the spatial channel directions at different subcarriers become separated from each other in the angle-domain,i.e,locate at different angle-domain samples.The beam split effect will induce frequencydependent sparse channel supports at different subcarriers.Consequently,the assumption of common sparse channel support does not hold,which means the existing schemes for millimeter-wave massive MIMO[18,19]will suffer from severe performance degradation in wideband THz massive MIMO systems.Although several channel estimation schemes for THz massive MIMO has been recently proposed,such as the low-rank matrix reconstruction based scheme[23]and the joint activity detection and channel estimation scheme[24],they have not considered the frequencydependent sparse channel support either.Hence,to the best of our knowledge,the wideband channel estimation in THz massive MIMO systems has not been well addressed in the literature.

1.2 Our Contributions

In this paper,we propose an accurate beam split pattern detection based wideband channel estimation scheme in THz massive MIMO systems.The specific contributions of this paper can be summarized as follows.

·We first analyze the angle-domain sparse structure of the wideband THz channel by considering the beam split effect.We prove that a series of index sets have the one-to-one match to different physical channel directions.These index sets are defined as beam split patterns,each of which is corresponding to a specific physical channel direction.By utilizing the one-to-one match between the physical channel direction and the beam split pattern,the physical channel direction can be accurately estimated.

·Based on the proof above,we propose a beam split pattern detection based wideband channel estimation scheme.For each channel path component,the physical channel direction is firstly estimated by exploiting the beam split pattern.Then,the sparse channel supports at different subcarriers are determined by using a support detection window.This support detection window is generated by expanding the beam split pattern,which is corresponding to the already obtained physical channel direction.The above procedure will be repeated path by path until all path components are considered.Finally,the wideband channel can be recovered by only calculating elements on the total sparse channel support containing sparse channel supports for different path components.Thanks to the one-to-one match between the physical channel direction and the beam split pattern,the proposed scheme can precisely estimate the physical channel directions and corresponding sparse channel supports.

·The physical channel direction estimation accuracy of the proposed scheme is analyzed,and it shows that the physical channel direction can be precisely estimated with a probability approaching 1.Extensive simulation results verify this analysis,and illustrate that the proposed beam split pattern detection based wideband channel estimation scheme can realize more accurate channel estimation than existing schemes.

1.3 Organization and Notation

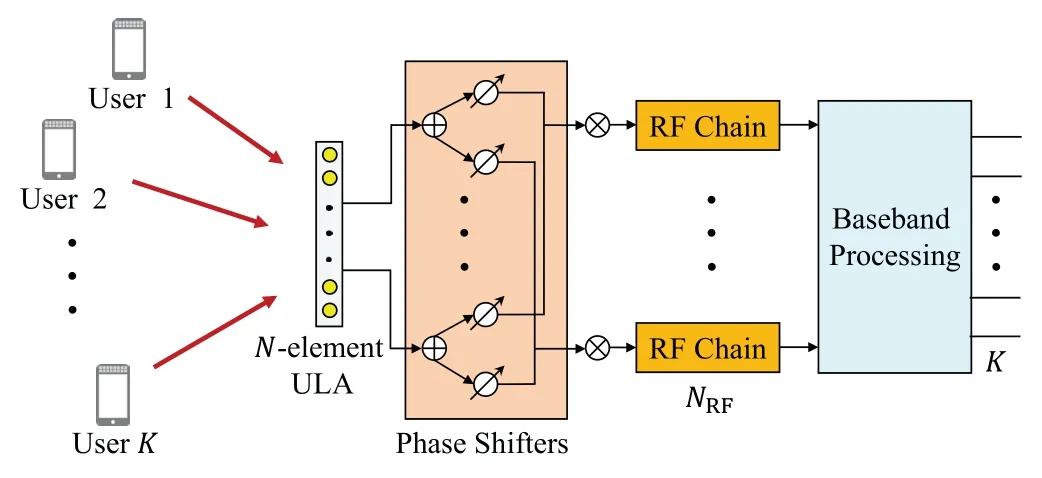
Figure 1.Wideband THz massive MIMO system with hybrid precoding.

The remainder of this paper is organized as follows.In Section II,the system model of a multi-user wideband THz massive MIMO system is introduced,and the channel estimation problem in this system is then formulated.In Section III,we first define the beam split pattern and prove the one-to-one match between the physical channel direction and the beam split pattern.Then,a beam split pattern based wideband channel estimation scheme is proposed,together with the corresponding performance and complexity analysis.Section IV illustrates the simulation results.Finally,conclusions are drawn in Section V.

Notation:(·)T,(·)H,(·)†,‖·‖F,and‖·‖kdenote the transpose,conjugate transpose,pseudo-inverse,Frobenius norm,andk-norm of a matrix,respectively;|·|denotes the absolute operator;H(i,j)denotes the element of the matrix H at thei-th row and thej-th column;If set Ξ=∪i{(ai,bi)},H(Ξ)denotes the vector composed of elements H(ai,bi);INrepresents the identity matrix of sizeN×N.

II.SYSTEM MODEL

In this paper,we consider an uplink time division duplexing(TDD)based multi-user wideband THz MIMO system with orthogonal frequency division multiplexing(OFDM).The hybrid precoding structure is employed at the BS to reduce energy consumption,as shown in Figure 1.The BS equips anN-antenna uniform linear array(ULA)[25],and utilizesNRFRF chains to serveKsingle-antenna users simultaneously withMsubcarriers.

2.1 Channel Model

We adopt the widely used Saleh-Valenzuela multipath channel model[26]in this paper.The channel hm∈CN×1between the BS and a specific user at them-th subcarrer(m=1,2,···,M)can be denoted as

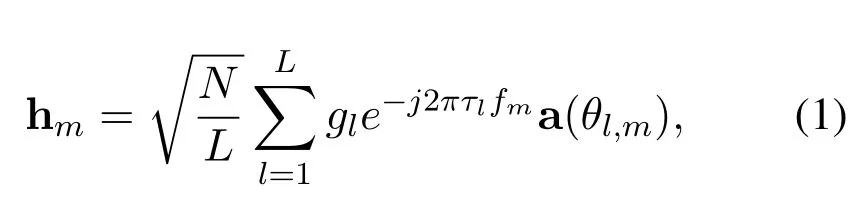
whereL,gl,andτlare the number of paths,the complex path gain of thel-th path,and the time delay of thel-th path,respectively,θl,mis the spatial channel direction of thel-th path at them-th subcarrier,and a(θl,m)is the steering vector ofθl,mwith the following form

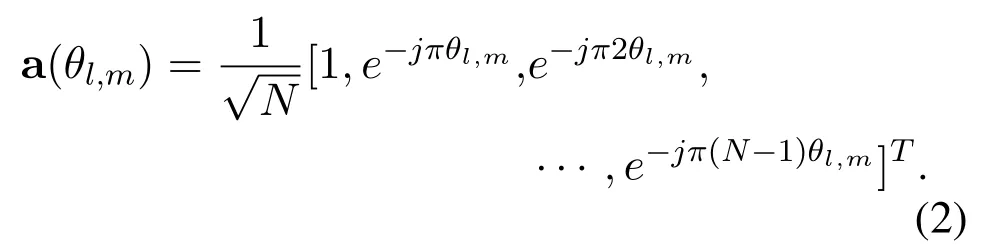
Futhermore,the spatial channel directionθl,mcan be represented as[26]

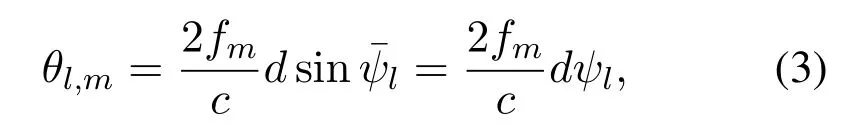
The channel hmcan be transformed to its angledomain representation by a spatial discrete Fourier transform matrix F∈CN×N.F containsNorthogonal steering vectors covering the whole angledomain as F=withn=1,2,···,N.These physical channel directions,n=1,2,···,Ncan be seen as the angle-domain samples of the channel physical channel directionψl.Correspondingly,the angle-domain channel∈CN×1can be denoted as

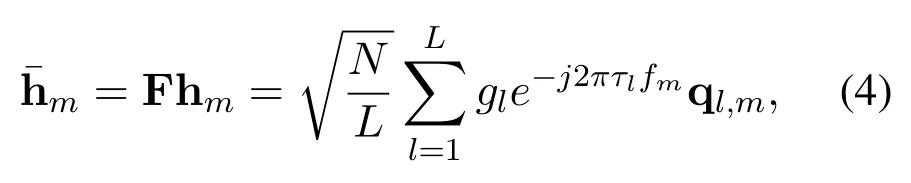
where ql,mdenotes the angle-domain representation of thel-th path component as

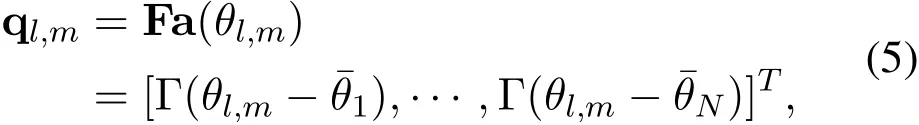
with Γ(x)=representing the Dirichlet Sinc function[27].Because of the power-focusing characteristic of the Dirichlet sinc functionΓ(x),the power of ql,mfocuses on a small number of elements decided by the spatial channel directionθl,m.Additionally,since the number of scatters is limited in THz band,the number of pathLis usually quite small(e.g.,L=3[28]).Therefore,we can conclude that the angledomain channel hmis a sparse vector,and the sparse support of the angle-domain channel hmis decided by spatial channel directionsθl,mform=1,2,···,M.

2.2 Problem Formulation

In TDD systems,uplink channel estimation is carried out at the BS based on the received pilots transmitted by users.As orthogonal pilots are widely used[26],we can consider an arbitrary user without loss of generality for uplink channel estimation.By utilizing the sparsity of the angle-domain channel,the wideband channel estimation problem can be formulated as a joint sparse recovery problem.

Specifically,we denotesm,pas the transmitted pilot at them-th subcarrier in the time slotp.Then,the received pilots ym,p∈CNRF×1at them-th subcarrier is

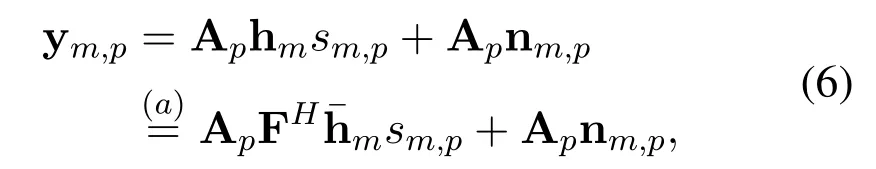
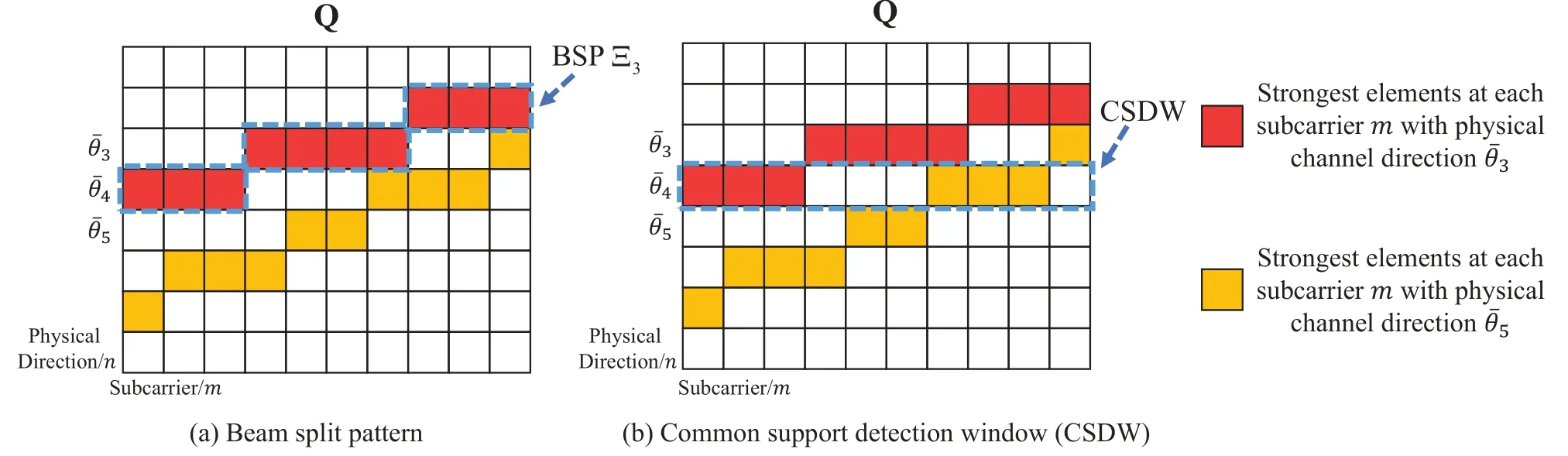
Figure 2.Illustration of the physical channel direction estimation with ψ1=θ3,ψ2=θ5,where Q=Q3+Q5:(a)Correct physical channel direction ψ1=θ3 can be estimated,since the BSP Ξ3 can exactly capture the channel power incurred by the physical channel directionθ3;(b)The existing assumption of a common sparse support will result in an incorrect estimate ψ1=θ4,because the highest power is captured atθ4 when common support detection window is utilized to estimate the physical channel direction.

where(a)comes from(4),Ap∈CNRF×Nis the frequency-independent analog combining matrix satisfyingdue to the hardware restriction(e.g.,realized by phase-shifters[29])1,and nm,p∈CN×1denotes the noise following the distribution nm,p～CN(0,σ2IN)withσ2being the noise power.DefinePas the length of transmitted pilots and assumesm,p=1 forp=1,2,···,P.Thus,the overall received pilots at them-th subcarriercan be denoted as

We can observe from(8)that the wideband channel estimation problem is formulated as a joint sparse recovery problem,where the target is to recover the wideband sparse angle-domain channel H based on the observation matrix A and the received pilots.The sparsity of the channel H makes compressive sensing algorithms efficient with a significantly reduced length of pilots,i.e.,NRFP≪N[18].Moreover,to further reduce the length of pilots and improve the channel estimation accuracy,existing wideband channel estimation schemes make use of the channel correlation by assuming channels at different subcarrier frequencies have a common sparse channel support[18,19].However,the ideal assumption of common sparse channel support may not hold in THz massive MIMO systems.Specifically,since the spatial channel directionθl,min(2)is frequency-dependent due to the beam split effect[21],the sparse supports of channelsat different subcarrier frequencies form=1,2,···,Mshould be quite different.This frequency-dependent sparse channel support will result in a severe performance loss for existing channel estimation schemes[18,19].Consequently,an accurate wideband channel estimation scheme is essential for THz massive MIMO systems.

III.BEAM SPLIT PATTERN DETECTION BASED CHANNEL ESTIMATION

In this section,we first define the beam split pattern based on the channel sparse structure,and reveal the one-to-one match between the physical channel direction and the beam split pattern.Then,by utilizing the one-to-one match,we propose the beam split pattern detection based channel estimation scheme to improve the estimation accuracy.Finally,the estimation accuracy analysis and complexity analysis of the proposed scheme are provided.

3.1 Beam Split Pattern of Wideband THz Channel

As described in Subsection 2.2,the beam split effect induces distinct spatial channel directionsθl,m,i.e.,different sparse supports of,at different subcarriers.Hence,it is hard to detect sparse channel supports accurately by using a common support detection window(SDW)at all subcarriers,like in existing schemes[18,19].To solve this problem,we reveal the oneto-one match between the physical channel directionψland a specific indexes set,which is defined as the beam split pattern(BSP).Specifically,the BSP contains the element indexes of the angle-domain channel with the largest power at each subcarrier.The following Lemma 1 provides a specific definition of BSP,and proves the one-to-one match between the physical channel direction and the BSP.

Lemma 1.Considering an arbitrary path component with the physical channel direction ψl,we defineQn=[ql,1,ql,2,···,ql,M]and n1∈{1,2,···,N}.When we assume the physical channel direction ψl locates on the angle-domain sampleswith ψl=,the BSPΞn defined as

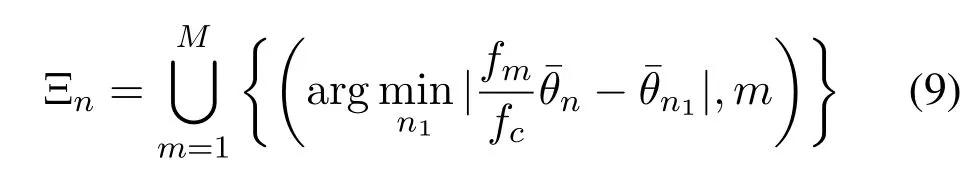
has a one-to-one match to the physical channel direction.

Proof.According to the analysis in[30],the element indexof the angle-domain representation ql,mwith the largest power is

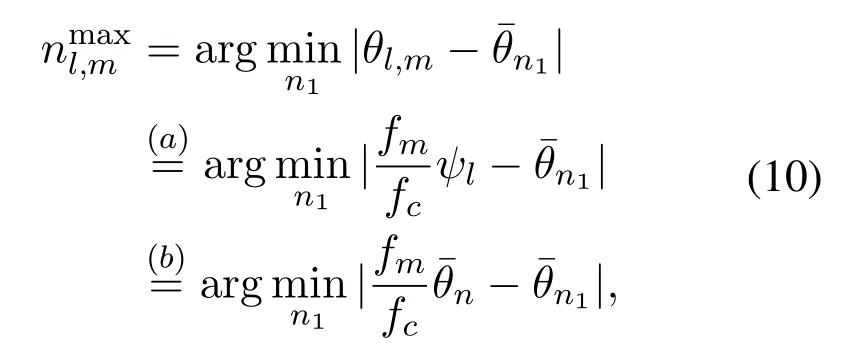
wheren1∈{1,2,···,N},(a)comes from(3)andd=c/2fc,and(b)comes from the assumptionψl=.Considering the definition of BSP in(9)and(10),we can conclude that the elements in BSP Ξnare,m=1,2,···,M.These elements are the element indexes of each column of matrix Qnwith the largest power.Denoteas a physical channel direction different fromψl=,wherebis a non-zero integer.Based on(10),for theM-th subcarrier,we can obtain

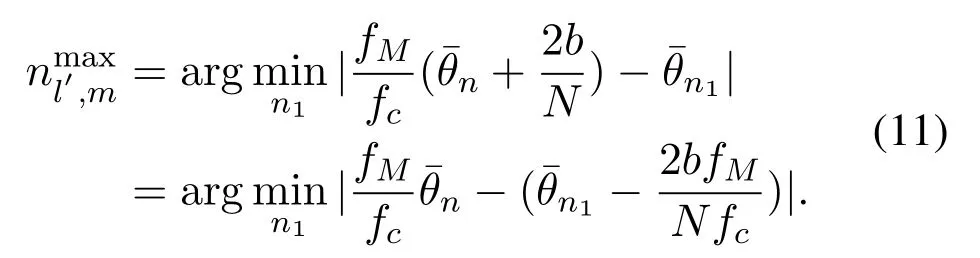
SincefM＞fc,we can simply get the element indexwith the largest power for the physical channel directionψl′at theM-th subcarrier satisfiesbased on(10)and(11).Thus,for a specific path component with the physical channel directionψl,the power captured by the BSP Ξnof Qnsatisfies

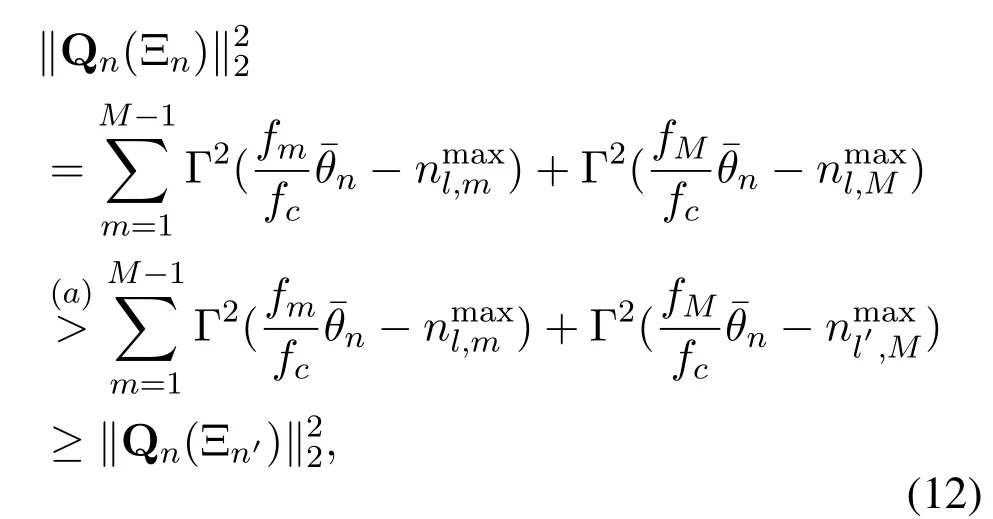
where(a)comes from(12)implies that when the physical channel directionψl=θn,the BSP Ξncan capture the most power of Qncompared with the BSP Ξn′of other physical channel directions.This means the BSP Ξncorresponds to a unique physical channel direction.Therefore,considering the BSP Ξnis defined by the physical channel direction in(9),we can conclude a one-to-one match between the physical channel directionand the BSP.

Lemma 1 indicates that the BSP Ξncan be utilized to estimate the physical channel directionψl,since it can be seen as a specific feature of the physical channel direction.Figure 2 compares the BSP and the common support detection window utilized in existing schemes[18,19]on physical channel direction estimation.We can see from Figure 2(a)that since the BSP Ξ3can exactly capture the channel power induced by channel path with physical channel direction,the correct physical channel directionψ1=can be detected.However,when the common support detection window is exploited as shown in Figure 2(b),the common support detection window captures the most power at.This is because due to the beam split effect,the path with physical channel directionψ1=andψ2=both generate channel power at.As a result,the common support detection window may cause estimation error.Then,the following Lemma 2 provides some insights on how to determine the sparse support of the channel based on the BSP.

Lemma 2.Defineas the SDWwhich is generated by expanding the BSPΞn,whereΘN(Ξn+b)is defined as the set composed of elements as(ΘN(a+b),e)when(a,e)belongs to the BSPΞn withΘN(x)=modN(x-1)+1,andΔis the size of the SDW.When the physical channel direction ψl locates on the angle-domain samplesas ψl=,the ratio γ between the power captured by the SDW ofQn and the power ofQn can be denoted as

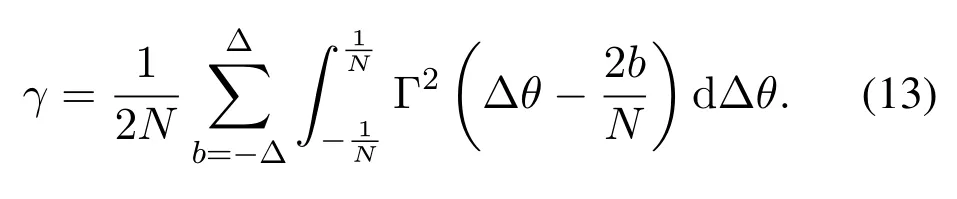
Proof.Based on the definition ofγ,we have

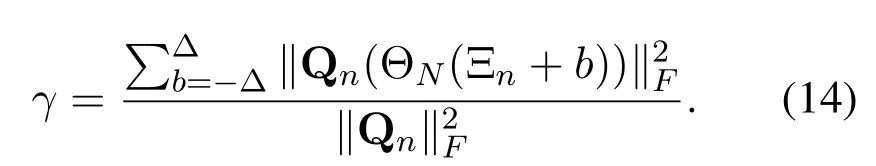
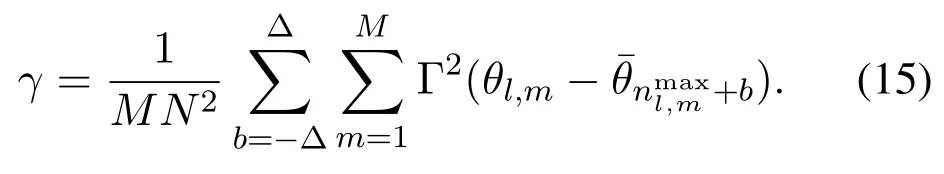
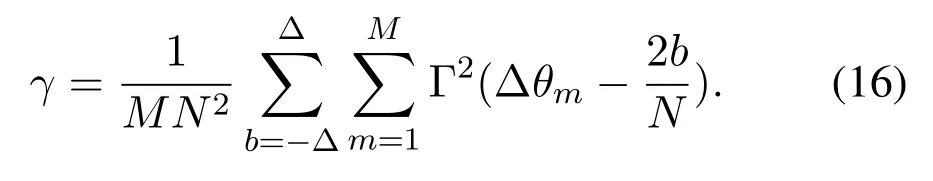
From(10),we know that the range ofΔθmisΔθm∈Since the number of subcarriersMis usually large(e.g.,M=512),we assumeΔθmdistributes uniformly in its range,i.e.,Δθm=Therefore,the summation onmin(16)can be rewritten by an integration form as

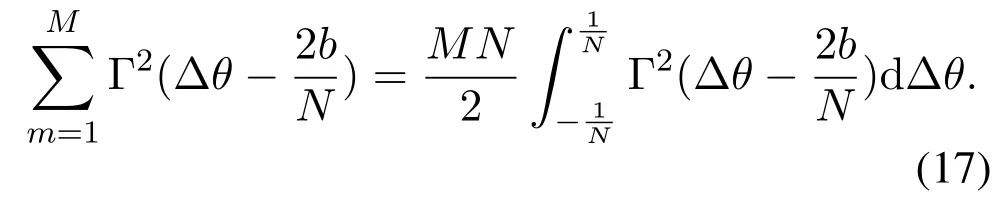
According to(16)and(17),(13)can be proved.

Lemma 2 indicates that the SDWs generated by expanding the BSP Ξncan capture most power of Qn.For instance,whenfc=100 GHz,B=15 GHz,N=256,M=512,andψl=,γ=97.7% power of Q40can be captured by the SDWIn contrast,when the physical channel directionψl/=,e.g.,ψl=we can only captureγ=0.6%power of Q50by utilizing the SDWThis observation means that after the physical channel directionψlis estimated by the BSP,the sparse channel supports at different subcarriers for thel-th path component can de directly obtained from the SDWs determined by the BSP.

3.2 Beam Split Pattern Detection Based Channel Estimation Scheme

Based on the BSP discussed above,we propose a beam split pattern detection(BSPD)based channel estimation scheme.The key idea is to estimate the physical channel directionψlby using the BSP at first,and then recover the sparse elements of thel-th path component by using the SDW generated by expanding the BSP.The above procedure will be carried out successively path by path until all path components are estimated.

The pseudo-code of the proposed BSPD based channel estimation scheme is shown in Algorithm 1.Firstly,we initialize the residual matrix U∈CPNRF×Mas U=[u1,u2,···,uM]=Y,where umdenotes the residual for them-th subcarrier.After that,we generateNBSPs Ξn,n=1,2,···,Naccording to(9)in step 2.Then,for thel-th path component,we estimate the physical channel directionψlbased on Lemma 1.Specifically,inspired by the idea in OMP or SOMP based scheme,we first calculate the correlation matrix C as C=AHU in step 4.In step 5,we utilize BSPs to capture the power of the correlation matrix C,and determine the indexof the physical channel direction of thel-th path component as

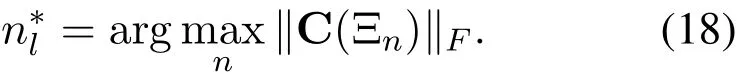
Algorithm 1.BSPD based channel estimation scheme.Require:Observation matrix:Y;Combining matrix:A Number of path components:L;SDWs size:Δ Ensure:Estimated angle-domain channelˆH =[ˆh1,ˆh2,···,ˆhM]1:U=[u1,u2,···,uM]=Y 2:Ξn=images/BZ_83_404_807_442_853.pngM m=1 images/BZ_83_525_791_556_836.pngimages/BZ_83_556_791_583_836.pngarg minn1|fm fcθn-θn1|,mimages/BZ_83_1083_791_1110_836.pngimages/BZ_83_1110_791_1140_836.png 3:for l∈{1,2,···,L}do m 16:end for 17:returnˆH=[ˆh1,ˆh2,···,ˆhM]

Thanks to the one-to-one match between the physical channel direction and the BSP in Lemma 1,(18)can guarantee the accuracy of the estimation on physical channel directionψl=.After the physical channel directionψlis obtained,sparse channel supports at different subcarriers can be decided according to Lemma 2.In step 6,we obtain the sparse channel supports Υlat different subcarriers for thel-th path component from the SDW generated by expanding the BSP,which is decided by the estimated physical channel directionThen,the influence of thel-th path component is removed to estimate remained path components.Specifically,we calculate the sparse channel support of thel-th path at them-th subcarrier Υl,min step 8 as Υl,m={i|(i,m)∈Υl}.After that,in step 9,non-zero elements of thel-th path components at them-th subcarrierˆsl,mare calculated according to the LS algorithm as

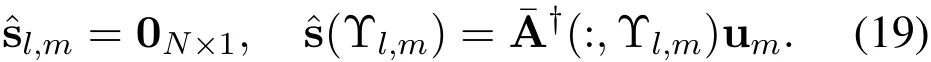
In step 10,we can remove the influence of thel-th path and update the residual matrix as

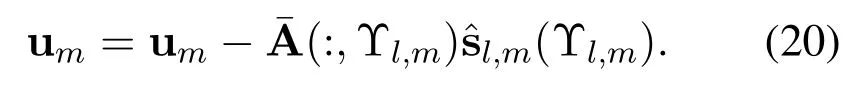
The procedure above is carried outLtimes until the sparse channel supports of all path components are estimated,where the number of path componentsLcan be obtained from channel measurement in advance[28].Finally,the angle-domain channel hm,m=1,2,···,Mis estimated based on these sparse channel supports.In specific,we calculate the sparse channel support of them-th subcarrier asΩm=Υ1,m∪Υ2,m∪···∪ΥL,min step 14.Then,we could obtain the estimated sparse angle-domain channel as

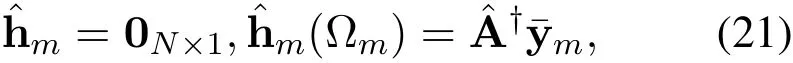
Notice that although the proposed scheme is inspired by the SOMP algorithm in[18,31],the proposed scheme has a major difference from the SOMP based scheme on how to detect the sparse channel supports.Specifically,in SOMP based scheme,the sparse supports are supposed to satisfy the common sparse support assumption.Therefore,the sparse supports are detected column by column where each column corresponds to a physical channel direction.On the contrary,the proposed scheme utilizes a two-step procedure to obtain sparse channel supports.Firstly,the physical channel directions are detected by using the defined BSP to capture the power of the channel.The elements in the BSP are determined by the beam split effect and not locate on a common position,which is quite different from the SOMP based scheme.Secondly,after the physical channel directions are obtained,the sparse supports are generated by expanding the BSPs which are determined by the obtained physical channel directions.Due to the beam split effect in the wideband THz massive MIMO channel,the ideal common sparse support assumption is not reasonable.Thus,the SOMP based scheme will face performance loss.While,since the proposed scheme makes use of the frequency-dependent sparse channel supports implied by the beam split effect,it can correctly detect the physical channel directions and corresponding sparse channel supports.Hence,the proposed scheme can achieve a better channel estimation accuracy.

3.3 Performance Analysis

In this subsection,we will analyze the estimation accuracy on physical channel directionsψlof our proposed BSPD based channel estimation scheme.We prove that the physical channel directionsψlwithl=1,2,···,Lcan be estimated precisely with a certain probability.Note that in the following analysis,we assume the physical channel direction for thel-th path component locates on the angle-domain samples satisfyingψl=θnl,which will only lead to a negligible physical channel direction estimation error when the number of antennas is huge in THz massive MIMO systems.

Firstly,we rewrite the angle-domain channel H in(8)to decouple different path components in H.Specifically,we define Υnas the set containing all the indexiin then-th BSP Ξnwith Υn={i|(i,m)∈Ξn,m=1,2,···,M}.For thel-th path component,since the rows indexed by Υnlcontains all the elements in BSP Ξnl,most of its power can be captured by Qnl(Υnl,:).Based on this property,we rewrite the angle-domain channel H as H=VB.The matrix B∈is defined as B=where

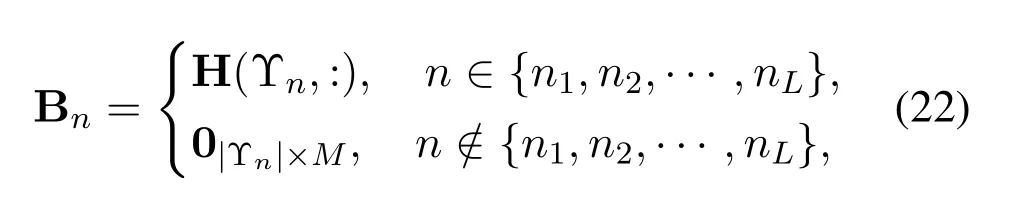
with H(Υnl,:)=glQnl(Υnl,:).Correspondingly,becomes a transformation matrix with V=[V1,V2,···,VN],where thei-th column of Vn∈CN×|Υn|only has one nonzero element at the index Υn(i)with Υn(i)representing thei-th element in the set Υn.This transformation H=VB can convert the angle-domain channel H into a block-wise form,where each path component is corresponding to a specific block in B.

With the help of the transformation H=VB,we can rewrite(8)as

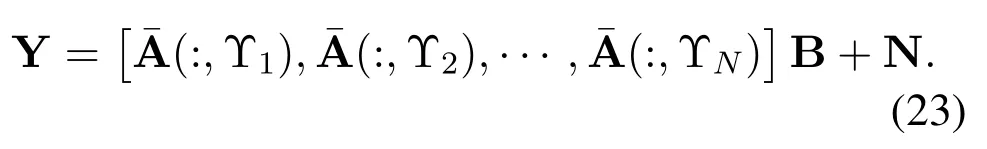
Then,to estimate the physical channel directionsψl,the key correlation matrix C is calculated as described in step 4 of Algorithm 1.Considering the transformation in(22),the correlation matrix C can be denoted as

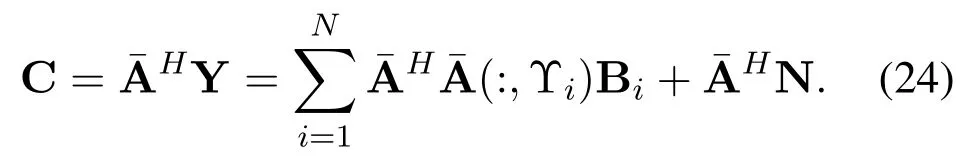
Therefore,the power captured by the BSP Ξn,which is utilized to estimate the physical channel directionψlas shown in step 5 of Algorithm 1,can be represented as

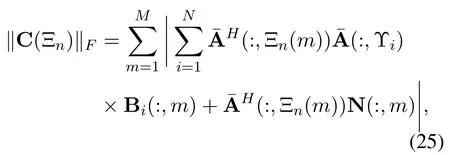
where Ξn(m)denotes the indexathat satisfies(a,m)∈Ξn.To illustrate the analysis clearly,we define an auxiliary parameterμto represent the subcoherence of the matrixas

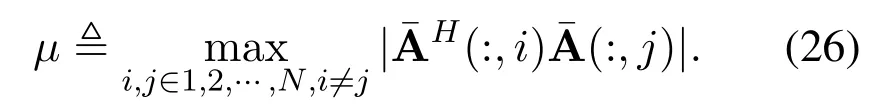
Note that the sub-coherence of the observation matrixdefined in(26)is widely utilized in the performance analysis of compressive sensing based algorithms[32].

Based on the definitions above,we prove the following Lemma 3,which provides a lower bound of the correct probability of the physical channel direction estimation for the proposed BSPD based scheme.Specifically,for a certain channel and a noise level,the physical channel directionψlcan be accurately estimated with a probability larger than a certain probability.The specific description and proof of Lemma 3 are illustrated as follows.

Lemma 3.For the l-th path component,we assume the physical channel direction ψl locates on the angle-domain samples as ψl=.When

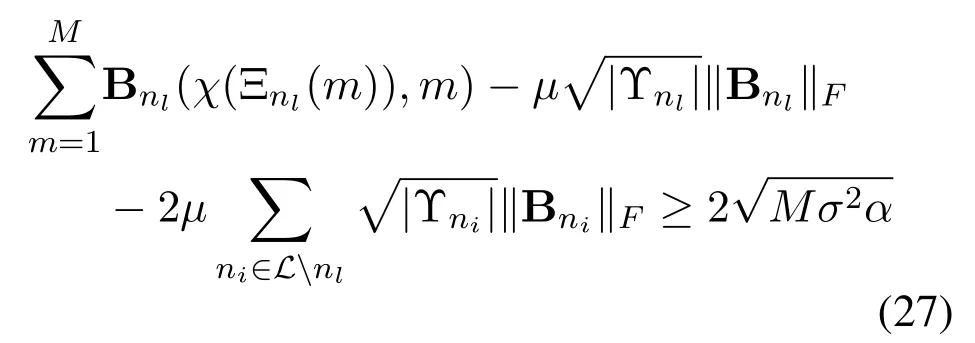
holds with χ(·)denoting the index transformation as χ(Ξnl(m))=Ξnl(m)-min Υnl+1and L={n1,n2,···,nL},the proposed BSPD based channel estimation scheme can accurately estimate ψl with a probability exceeding

with α is a constant.

Proof.See Appendix A.

Lemma 3 indicates that for a certain channel and a noise level,the correct probability of the physical channel direction estimation can be lower-bounded by(28).We can observe from(28)that when the correct probability in(28)locates in the feasible domain asthe correct probability will monotonically increase from 0 to 1 rapidly whenαgrows up.Therefore,considering that the allowedαis large givenμand‖Bn‖Fwhen the noise powerσ2is relatively small,the correct probability of the physical channel direction estimation will approach 1 with a low noise level.Therefore,we can conclude that the proposed BSPD based channel estimation scheme is able to accurately estimate physical channel directions when the noise power is relatively small.This conclusion will be verified by simulation results in Section IV.

3.4 Complexity Analysis

In this subsection,we will provide the complexity analysis of the proposed BSPD based channel estimation scheme based on the number of complex multiplications.The complexity of the OMP and SOMP based schemes[18,19]are also shown for comparison.

We can observe from Algorithm 1 that the complexity of the proposed BSPD based scheme is mainly determined by steps 4,5,9,10,and 15.Specifically,in step 4,the correlation matrix C is calculated by C=HU.Since the dimension ofand U are∈CNRFP×Nand U∈CPNRF×M,we know that the complexity of step 4 isO(NRFPNM).Then,we compute the norm of C(Ξn)of sizeM×1 forNtimes in step 5.Therefore,the complexity of step 5 should beO(MN).In step 9,the non-zero elements at each subcarriermare calculated as(19),where the pseudoinverse of(:,Υl,m)∈CNRFP×(2Δ+1)is generated together with the multiplication between(:,Υl,m)and um∈CNRFP×1.Consequently,step 9 requires the complexityO(MNRFPΔ2).Similarly,the complexity of step 10,which contains a multiplication between(:,Υl,m)and∈CNRFP×1,isO(MNRFPΔ).In addition,the sparse angle-domain channel at each subcarriermis recovered in step 15 with a multiplication between(:,Ωm)∈CNRFP×(L(2Δ+1))and ym∈CNRFP×1.Therefore,the step 15 involves the complexity ofO(MNRFPL2Δ2).Finally,considering that steps 4,5,9,and 10 are carried out forLtimes,the total complexity of the proposed BSPD based scheme can be represented as

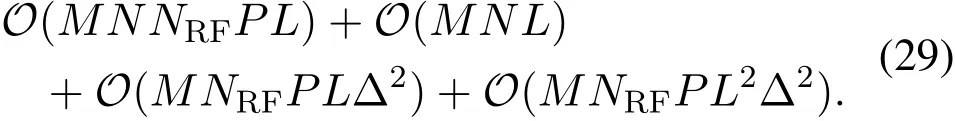
For comparison,both the OMP and SOMP based channel estimation schemes require the complexity ofO(MNNRFPLΔ)+O(MNRFPL3Δ3)[18,19].Generally,due to the sparsity of the THz channel,the size of the SDW is relatively small,e.g.,Δ=4≪N=256.Therefore,we can conclude that the proposed BSPD based scheme enjoys a lower complexity than the existing OMP and the SOMP based schemes[18,19].

IV.SIMULATION RESULTS

In this section,we provide simulation results for the proposed BSPD based channel estimation scheme.We consider a multi-user THz wideband MIMO-OFDM system.The system parameters are set as:N=256,K=8,NRF=8,fc=100 GHz,B=15 GHz andM=512.Note thatB=15 GHz is a reasonable setting for THz systems to reach target transmission rate as 1 Tb/s in future 6G networks[3].The multipath THz channel is generated with the following parameters:and maxl τl=20 ns.Finally,the signal-to-noise ratio(SNR)is defined as

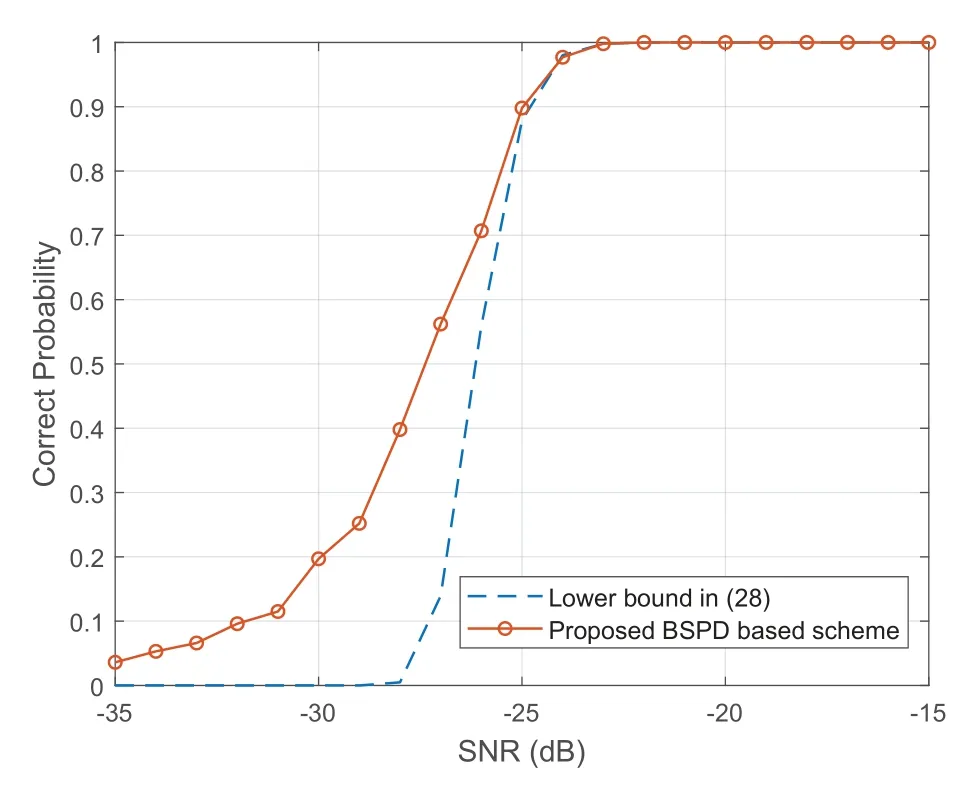
Figure 3.The correct probability of the physical channel direction estimation of the proposed BSPD based channel estimation scheme.

Figure 3 provides the physical channel direction estimation accuracy of the proposed BSPD based scheme.We set the physical channel directions of the channel path components asψ1==0.5039,ψ2==-0.8711,ψ3==-0.3008.The probability that the proposed BSPD based scheme could correctly estimate the physical channel directionψ1is shown in Figure 3.Besides,the lower bound of the correct probability of the physical channel direction estimation,which is proved by Lemma 3,is also illustrated for comparison.From Figure 3,we can observe that when the SNR is larger than-25 dB,the proposed BSPD based scheme has the ability to obtain the correct physical channel direction with a probability of 1.This indicates that the proposed scheme can estimate the physical channel direction accurately even in low SNR regions.Moreover,we can observe that the correct probability of the physical channel direction estimation achieved by the proposed scheme is tightly lower-bounded by the bound proved in Lemma 3,which is consistent with our analysis in Subsection 3.3.

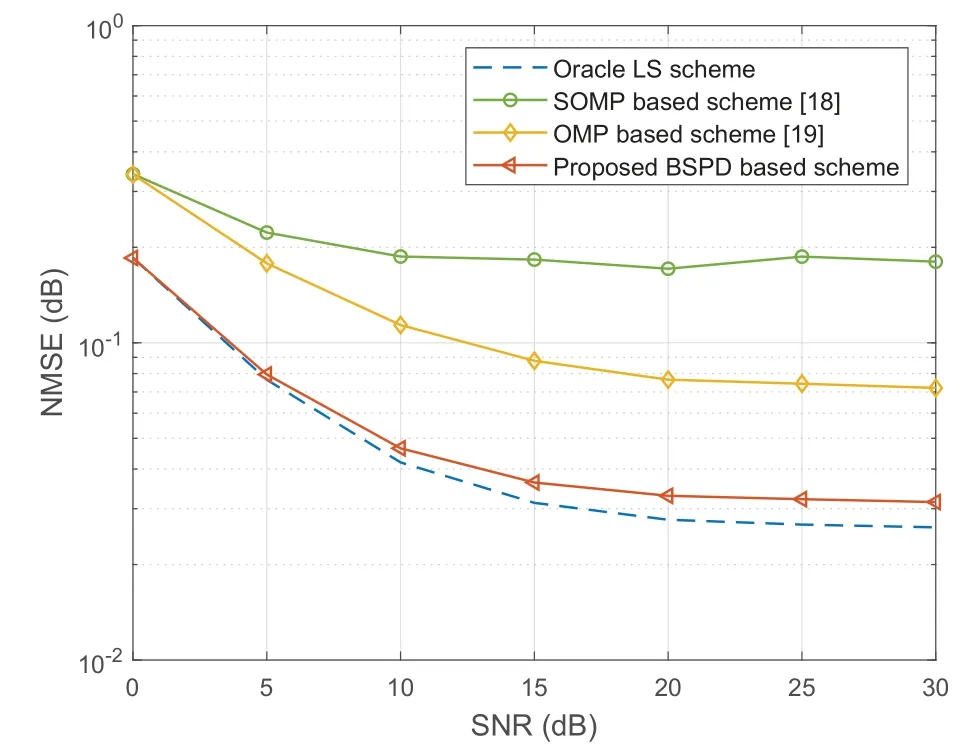
Figure 4.NMSE performance comparison against SNR.

Figure 4 illustrates the normalized mean square error(NMSE)performance against SNR of the proposed BSPD based scheme and existing schemes,including SOMP based scheme[18]and OMP based scheme[19].For the OMP based scheme,we carry out the OMP algorithm once every 16 subcarrier.Then,the sparse channel supports of these 16 subcarriers are obtained by the OMP algorithm based on the common support assumption.For all considered schemes,P=10 time slots per user are utilized for pilot transmission.The size of SDWs is set asΔ=4 for the proposed BSPD based scheme.For a fair comparison,we assume the sparsity level in OMP based scheme and SOMP based scheme isL(2Δ+2)=27.The oracle LS scheme is also considered as a benchmark for comparison,where the sparse channel supports of the wideband channel hmare assumed to be known perfectly.We can observe from Figure 4 that the proposed BSPD scheme outperforms existing schemes[18,19]in all SNR regions.This is because the BSPD based scheme exploits the specific sparse property of the wideband channel with the beam slit effect.Moreover,our proposed BSPD scheme can approach the NMSE performance of the ideal oracle LS scheme.

Figure 5 provides the NMSE performance against pilot lengthP,where SNR is set as 20 dB.Other parameters are the same as those in Figure 4.We can observe from Figure 5 that the NMSE achieved by all schemes decrease as the pilot sequence becomes longer.In all considered length of pilotsP,the proposed BSPD based scheme can achieve better NMSE performance than existing schemes,and it can approach the NMSE performance of the ideal oracle LS scheme.Particularly,in the case with a short length of pilots(e.g.,P=4 andP=8),the performance gap between the proposed BSPD based scheme and existing schemes is quite large.This indicates that the BSPD based scheme can efficiently reduce the pilot overhead for channel estimation.

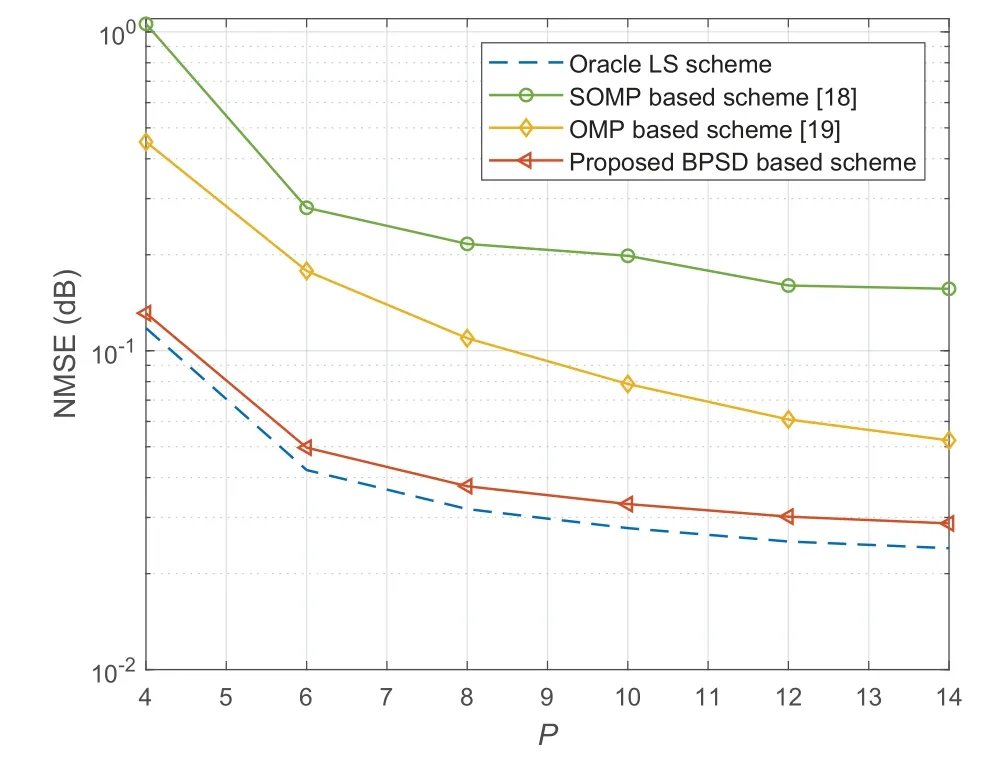
Figure 5.NMSE performance comparison against the pilot length P.

Figure 6 shows the NMSE performance against the bandwidthB.The range of the bandwidth is from 1 GHz to 15 GHz,and other parameters are set as SNR=20 dB andP=10.We can observe from Figure 6 that when the bandwidth is small,e.g.,1 GHz,both the SOMP based scheme and the proposed scheme can achieve the near-optimal NMSE performance.However,when the bandwidth becomes larger,the NMSE performance of the SOMP and OMP based scheme gradually degrade.This is because the assumption of a common sparse channel support utilized in the SOMP and OMP based schemes cannot deal with the frequency-dependent sparse channel supports caused by the beam split effect.In contrast,the proposed BSPD based scheme is robust to the bandwidthB,and can achieve the near-optimal NMSE performance with different bandwidths.

V.CONCLUSION

In this paper,we investigated the channel estimation problem in wideband THz systems,where the beam split effect was considered.We proposed an efficient BSPD based wideband channel estimation scheme.Firstly,we proved the one-to-one match between the physical channel direction and the BSP,and the SDW generated by expanding the BSP corresponds to the sparse supports of the channel path component.Based on this proof,we propose to estimate the physical channel directions by using the BSPs,and then recover the sparse channel supports by exploiting the SDWs generated by expanding the BSPs.Simulation results show that the proposed scheme can achieve better NMSE performance than existing schemes.

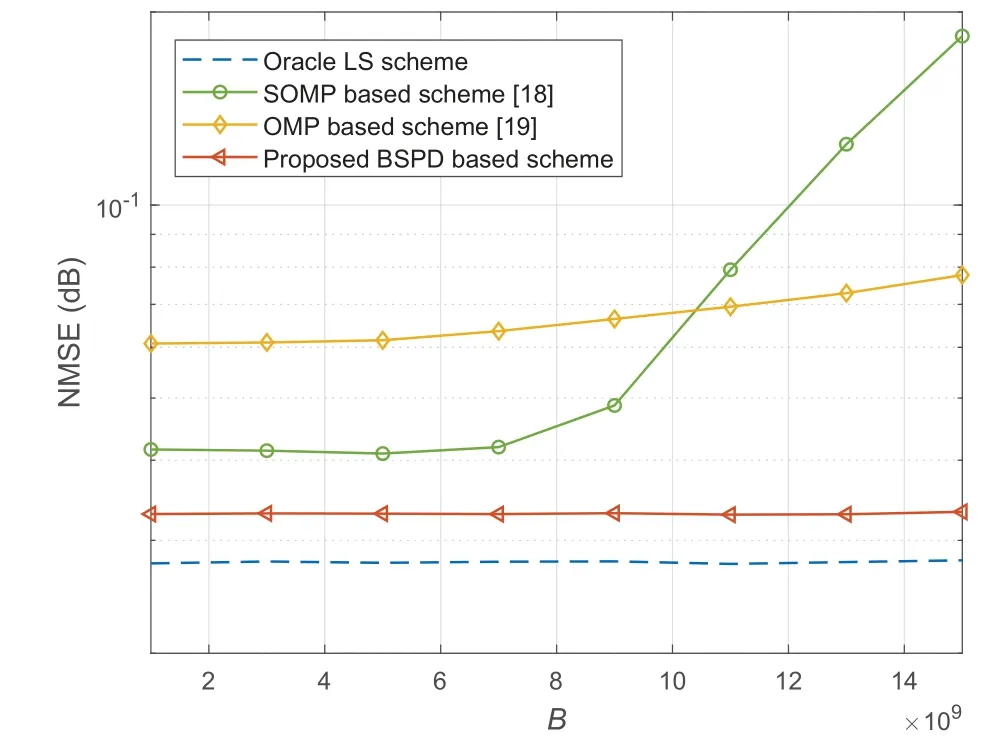
Figure 6.NMSE performance comparison against the bandwidth B.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China(Grant No.2020YFB1805005),in part by the National Natural Science Foundation of China(Grant No.62031019),and in part by the European Commission through the H2020-MSCA-ITN META WIRELESS Research Project under Grant 956256.

APPENDIX A.PROOF OF LEMMA 3

Proof.For thel-th path component,the physical channel directionψlcan be accurately estimated if

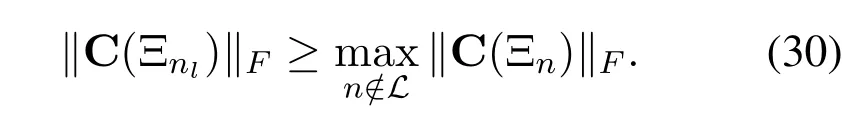
We consider a specific caseDthat the noise term in(25)is bounded by a constantγas

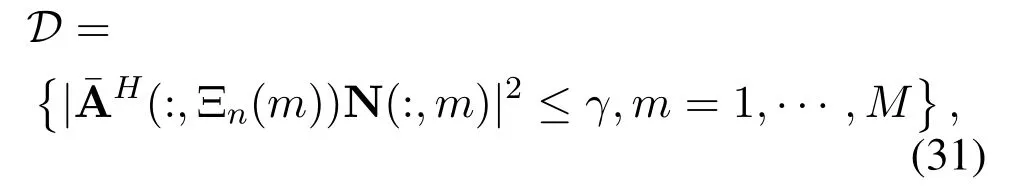
whereγis defined asγ=σ2α.Based on Lemma 4 proved in Appendix B,the caseDwill occur with a probability exceeding(28).

In this case,we can bound the right side of(30)according to(25)as

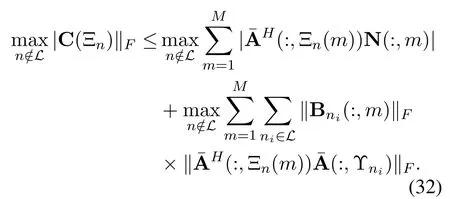
Considering the noise matrix N is composed ofMvectors with Gaussian distribution and caseDhappens,we can obtain

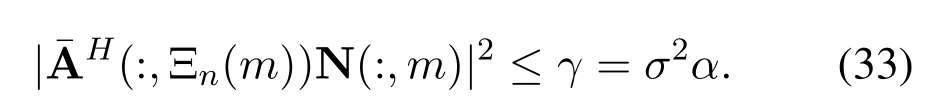
In addition,due to the definition ofμin(26),we haveTherefore,consideringwe can obtain the upper bound of the right side of(30)as

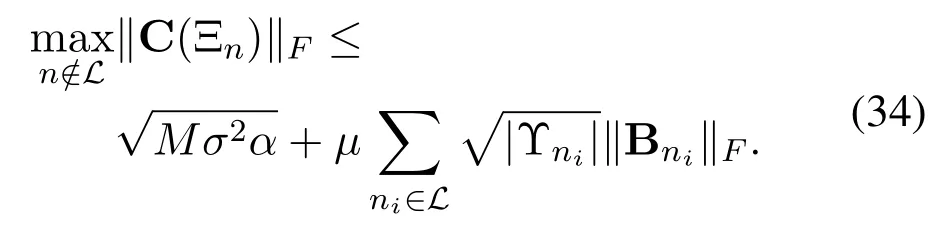
On the other hand,we can obtain the lower bound of the left side of(30)as

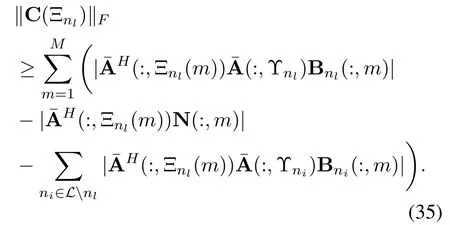
Based on the definition of the analog combining matrix,we know thatHence,the first term in the right side of(35)can be bounded as

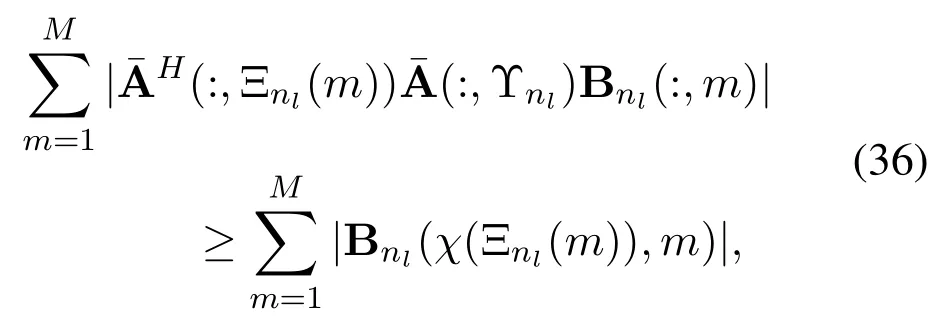
whereχ(·)denotes the index transformation asχ(Ξnl(m))=Ξnl(m)-min Υnl+1.Similar to(33),we can bound the second term in the right side of(35)asThen,according to the operation on the second term in the right side of(32),the lower bound of the third term in the right side of(35)can be represented as

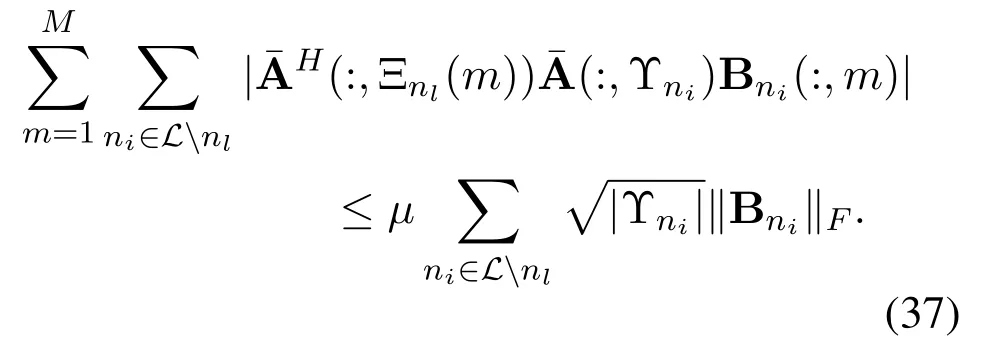
Combining the above analysis in(36)and(37),we can conclude that

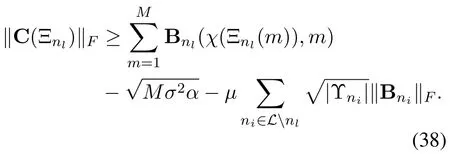
Therefore,based on the bounds in(34)and(38),we can conclude that when

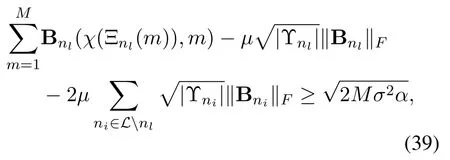
(30)is guaranteed under the caseD,and consequently the physical channel directionψlcan be accurately estimated with a probability exceeding(28).Thus,the proof is completed.

APPENDIX B.LEMMA 4

Lemma 4.Assuming each column of the noise matrixNin(8)is a Gaussian vector satisfyingN(:,m)～CN(0QNRF,σ2IQNRF),we have the probability that the case D in(31)happens satisfies

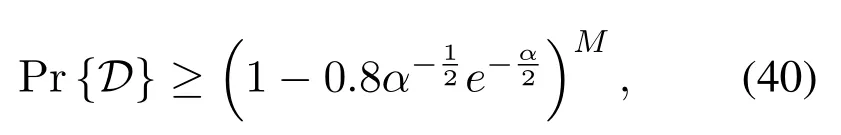
where γ is defined as γ=σ2α.

Proof.We first consider a certain subcarrierm.Since the noise vector N(:,m)is a Gaussian vector,(:,Ξn(m))N(:,m)in the caseDshould satisfy Gaussian distribution.The mean and the variance of(:,Ξn(m))N(:,m)are 0 andσ2(:,Ξn(m))(:,Ξn(m)).We have

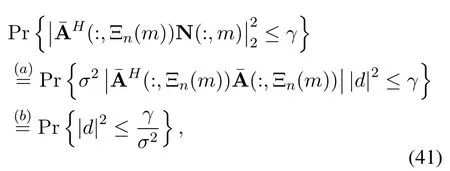
where(a)comes from definingdas a unit Gaussian variable with mean 0 and variation 1,and(b)comes from

To obtain the probability Prwe list a useful lemma[32]as follow.

Lemma 5.When d is a unit Gaussian variable with mean0and variation1,we have

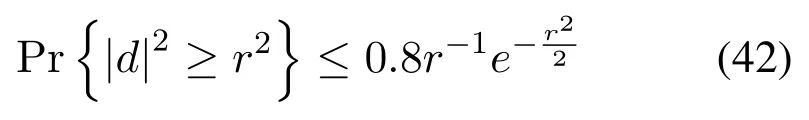
Proof.See Lemma 4 in[32].

Based on(42)in Lemma 5,we have

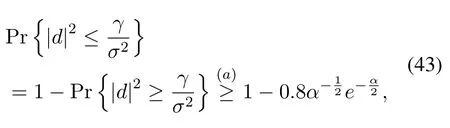
where(a)comes from(42)andγ=σ2α.Considering that the caseDin(31)indicatesholds for all subcarriersm=1,2,···,M,we can obtain

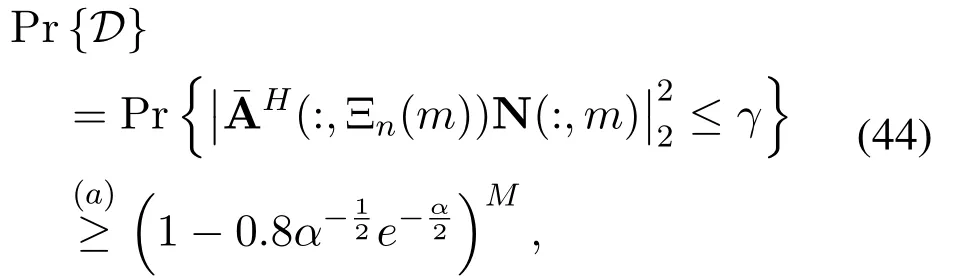
where(a)comes from(43).Therefore,the proof is completed.