含随机噪声地震数据重建的稀疏反演模型与算法
朱跃飞,曹静杰
1.河北省战略性关键矿产资源重点实验室,河北 石家庄 050031;2.河北地质大学 地球科学学院,河北 石家庄 050031
0 引言
地震勘探的野外数据采集经常会由于成本、地表环境、坏道等因素造成一些地震道数据的缺失,为了避免缺失的地震道对后续数据处理的影响,需要对缺失的地震数据进行重建。地震数据重建能够由不满足采样定理的数据重建出规则且满足采样定理的数据,避免成本昂贵的重新野外采集,消除不完整数据对叠前时间偏移[1],三维表面多次波消除[2]和时移地震[3]的影响。地震数据重建方法有很多种,主要分为基于信号处理的方法[4-8],基于波动方程的方法[9-11]和矩阵或张量完备的方法[12-14],最近基于机器学习和人工智能的方法正在兴起[15-16]。基于信号处理的方法具有计算效率高、数值效果稳定和抗噪性强的优点,是目前学术界和工业界的主流研究方向,该类方法又可以分为基于预测误差滤波的方法[4]和基于稀疏变换的方法[5-8]。基于矩阵和张量完备的方法是最近几年新兴的研究方向,数值效果同样可靠。在地震数据采集过程中,由于环境噪声、仪器设备等原因,采集到的地震数据经常含有各种噪声,因此含噪声地震数据的重建是地震数据重建问题中的一个新的研究分支。该方法避免了含噪声数据的先去噪后重建,或者先重建后去噪,将重建和去噪合二为一减少了工作量并且和先重建后去噪具有相当的效果[17],最近对含噪声数据重建的研究逐渐增多。Hennenfent和Herrmann(2006)提出了基于一种非规则采样Curvelet变换[18]和迭代阈值法的地震数据重建和去噪;Oropeza和Sacchi(2011)基于矩阵完备理论提出了一种同时重建和去噪的加权重插入方法来消除随机噪声[12],Gao等人(2013)基于傅里叶变换提出一种加权凸集投影方法来同时重建和去噪[19],然而上述两种算法都没有给出求解的数学模型。曹静杰和王本锋(2015)证明了加权凸集投影法是求解无约束反演模型的算法,其权重因子能够放大阈值从而实现去噪[17]。凸集投影法是地震数据重建中使用较多的方法,具有很好的数值效果和计算速度,但是Abma和Kabir(2006)的文章以Fourier变换为稀疏变换[20],只是给出了算法的迭代过程,学者们对其求解的数学模型仍然模糊不清。
文章首先阐述了基于稀疏变换和矩阵完备理论的地震数据重建的模型和算法,总结了一些可以作为稀疏约束的正则算子;然后给出了凸集投影法的推导过程,证明了其是求解等式约束模型的算法,该方法只对不含噪声数据的重建有效。对于反问题来说反演模型的建立是最重要的,当模型选择正确后正则参数是否合适决定了反演的数值效果。在这两者的基础上选择合适的解法才能提高反演的精度和效果。正则参数的选择决定基于稀疏反演的含噪声数据的重建问题的成败,目前关于含噪声数据重建的文章对正则参数的选择几乎没有讨论,因此文章列出几种正则参数的选择准则和方法。在数值模拟部分用一种简单的阈值算法来求解反演模型,二维模拟数据、二维真实数据和三维真实数据的数值试验证明了只有选择合适的正则参数含随机噪声数据的重建才能达到好的效果。
1 地震数据重建模型与解法
地震数据采集过程可以表示为如下的线性过程:
Φd+n=dobs
(1)
其中Φ是采样矩阵,d是未知的完整波场数据,n是可加噪声,假设n为随机白噪声,dobs为采样的不完整数据。如果完整的波场数据d在某个变换域是稀疏或者可压缩的,即x=Ψd是稀疏或者可压缩的,则公式(1)可以表示为:
ΦΨ*x+n=dobs
(2)
其中Ψ*为Ψ的共轭转置(一般选择Ψ是正交变换或者紧框架)。由于采样数据的不完整性,公式(2)是欠定方程组,存在无穷多解。基于x的稀疏性假设,公式(2)的稀疏解可以通过解如下的优化问题找到:

(3)
其中σ是噪声的能量,0表示非零元素的个数。0不是连续可微的,因此问题(3)不存在多项式解法,常用1范数代替0范数作为目标函数,建立如下的基追踪问题[21]:

(4)
当x求出后,则可以由Ψ*x求出d。
基于矩阵完备理论的重建方法是另一种常见的重建方法,该方法需要假设同相轴是线性的,假设完整的地震数据可以重排为一个低秩矩阵,根据重排矩阵的低秩性约束来建立矩阵优化模型。地震数据可以重排为块Toeplitz或块Hankel矩阵[11],除此之外还有一些其他的重排方式[21-22]。假设完整的地震数据d重排为Md,采样矩阵Φ重排为MΦ,噪声n重排为Mn,采样数据dobs重排为Mdobs,公式(1)可以变为:
MΦ·Md+Mn=Mdobs
(5)
根据矩阵的低秩约束,可以建立如下的矩阵优化问题:
minΛ(Md)0s.t.MΦ·Md-MdobsF≤ρ
(6)
其中Λ(Md)0表示Md的奇异值的个数,Λ(Md)为由Md的奇异值组成的向量,该矩阵优化问题同样不存在多项式解法,一般采用矩阵Md的核范数来代替Λ(Md)0,建立如下模型:
minMd*s.t.MΦ·Md-MdobsF≤ρ
(7)
其中Md*=Λ(Md)1表示Md的核范数,·F表示矩阵的F范数。
当地震数据噪声很弱时,可以假设σ≈0,则问题(4)变为:
minx1s.t.ΦΨ*x=dobs
(8)
如果以时间-空间域的变量为未知数,公式(8)又可以表示成:
minΨd1s.t.Φd=dobs
(9)
同理当ρ≈0时,问题(7)可以退化为:
minMd*s.t.MΦ·Md=Mdobs
(10)
或者
minF(d)*s.t.Φd=dobs
(11)
其中F(d)=Md表示对数据d重新排成Md的过程。
当地震数据中的噪声不可忽略时,σ>0或者ρ>0,此时直接解问题(4)和问题(7)相对困难,一般求解它们的无约束形式:
(12)
或
(13)
其中λ为正则参数,用来平衡数据拟合误差和解的稀疏性(或者低秩性)。反演理论表明对于每个σ和ρ,存在唯一的λ使得约束优化问题(4),(7)和无约束优化问题(12),(13)存在相同的解[28-23]。对于含噪声数据重建,一般求解的是(12),(13)或者它们的变形:
(14)
和
(15)
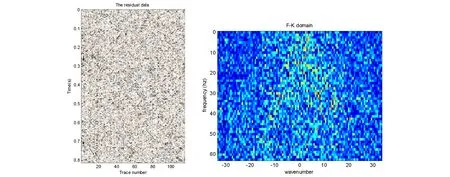
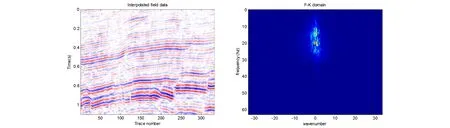
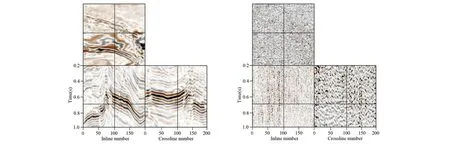
除了上述的1范数作为稀疏约束,还可以采用Cauchy函数,Huber函数[24],1范数的光滑近似函数[25],p-范数(0 凸集投影法是一种重要的重建算法,该算法计算效率高,数值效果稳定,是工业界常用的方法。该方法的每次迭代由两部分组成,第一步是当前迭代解在变换域的阈值运算,第二步通过往凸集上的投影升级迭代解。Abma和Kabir(2006)将该方法引入地震数据处理领域时只给出了求解过程[20],并没有给出求解的数学模型。对于重建问题来说该方法求解的是问题(9),即凸集投影法解的是等式约束问题。 (16) (17) 令步长α等于μ,则: (18) (19) dk+1=dobs+(I-Φ)Ψ*Tμ(Ψdk) (20) 根据上面关于凸集投影法的推导可知软阈值运算是专门针对1范数正则化产生的,变换域的阈值运算可以看作变换域的去噪,阈值类算法实现含噪声数据重建的关键是选择合适的阈值,阈值和上述的正则参数是等价的,该参数和噪声的能量有关,当噪声能量较大时,选择较大的阈值,当噪声能量较小时选择较小的阈值。 经典的迭代软阈值法是解问题(12)的方法[27],SPGL1方法通过解问题(4)来实现稀疏解的求取[23],这两种方法都适合含随机噪声数据的重建。曹静杰和王本锋(2015)证明了加权凸集投影法是解无约束优化问题(14)的方法[17],根据加权凸集投影法的推导过程可知,Oropeza和Sacchi(2011)中加权重插入算法是解矩阵优化问题(15)的算法[12]。该算法通过对重排矩阵Md的奇异值不断的作阈值运算来重建低秩矩阵,秩的作用如同变换域的系数个数,该方法同样要确定最小特征值的大小和权重,而权重可以放大最小特征值,因此该方法和加权凸集投影法的思想是一致的。Wang等(2011),Cao和Wang(2014)提出用信赖域算法解以1范数为信赖域的模型[28-29],同样能够实现稀疏解的求取,证明了在合适的模型下,信赖域方法同样可以作为稀疏解法。除此之外还有很多解上述模型的算法,请参考Cao等[25]。 对于无噪声地震数据重建,同样可以解上面的无约束优化形式,其中的正则参数只要取非常小的正数,因此对于不含噪声数据的重建,正则参数的选取不存在问题。但是当噪声能量不可忽略时,正则参数的作用举足轻重,目前的含噪声地震重建的文章和算法大都没有详细讨论如何确定合适的正则参数。论文对正则参数的选择准则进行梳理,列出几种正则参数的选择方法。λ是σ的隐函数,即两者不存在显示关系。这两种参数都可以看作是正则参数,在反演理论中,存在两种策略来估计正则参数:先验的策略和后验的策略[30]。先验策略指的是在计算之前确定正则参数,但是先验策略只有理论分析意义,实用性不大。后验策略指的是在求解过程中估计正则参数,该类方法的实用性较强,比如Morozov偏差原则,广义偏差原则,交叉检验原则,L曲线等方法[30],前三种方法都需要知道噪声的能量。即使正则参数λ给定,在求解时也往往采用同伦法求解,其思路是求解λ逐渐下降的一系列无约束模型直到给定的λ,用上一个模型的解作为下一个模型的初始解,这样可以防止得到局部最优解。 下面给出算法1求解1范数正则化的模型(14)来证明当反演模型给定时,正则参数正确与否决定含噪声数据的重建和去噪的效果。 算法1: 第一步:输入采样数据dobs,采样矩阵Φ,稀疏变换Ψ,最大迭代次数N,噪声能量的估计ε,最小阈值τmin,令k=0。 第三步:通过软阈值运算求出变换域的系数αk+1=Tτk(ΨT(dk+rk)),返回时间-空间域的解dk+1=Ψαk+1。 第五步:输出最终结果df=dN。 将Morozov偏差原则和迭代次数结合起来作为停机准则。算法1的阈值下降方式采用指数下降[19],τ的下降对应于正则参数λ的下降。 图1 (a)不含噪声模拟数据;(b)不含噪声模拟数据的F-K谱Fig.1 (a)Noise-free synthetic data;(b)F-K spectrum of Fig.1a 图2 (a)含随机噪声的数据,信噪比为6.3963 dB;(b)含随机噪声数据的频谱Fig.2 (a)Noisy synthetic data with SNR=6.3963 dB;(b)F-K spectrum of Fig.2a 图3 (a)随机采样的含噪声数据,信噪比2.6498 dB;(b)随机采样的含噪声数据的F-K谱Fig.3 (a)Randomly sampled noisy data with SNR=2.6498 dB; (b)F-K spectrum of of Fig.3a 图4 (a)阈值为0.2时的重建结果,信噪比13.7644 dB;(b)图4a的F-K谱Fig.4 (a)Interpolated result with the least threshold value 0.2,SNR=13.7644 dB;(b)F-K spectrum of Fig.4a 图5 (a)阈值为0.01的重建结果,信噪比7.1445 dB;(b)图5a的F-K谱.Fig.5 (a)Interpolated result with the least threshold value 0.01,SNR=7.1445 dB;(b)F-K spectrum of Fig.5a 图6 (a)图5(a)与原始数据的误差;(b)图6(a)的F-K谱.Fig.6 (a)Difference between Fig.5a and the original noiseless data;(b)F-K spectrum of Fig.6a 图7(a)是一个时间采样点为276,含有232道的二维地震剖面,时间采样率为4毫秒,道间距为25米,该数据含有一定程度的噪声,图7(b)是该数据的F-K谱;图8(a)为图7(a)随机采样50%道的结果,图8(b)为其F-K谱;图9(a)为阈值法的结果,由图9(a)可以看出不仅实现了重建而且提高了信噪比。图9(b)为其F-K谱。最小阈值为0.04,该阈值经过测试得到,采用60步迭代。图10(a)为原始数据与重建结果之差,几乎不存在有效信号,图10(b)为图10(a)的频谱。 图7 (a)含噪声二维剖面;(b)图7(a)的F-K谱Fig.7 (a)Noisy 2D field data;(b)F-K spectrum of Fig.7a 图8 (a)随机采样50%地震道的二维剖面;(b)图8(a)的F-K谱Fig.8 (a)Randomly sampled data with 50% traces missing;(b)F-K spectrum of Fig.8a 图9 (a)迭代阈值法的重建结果;(b)图9(a)的F-K谱.Fig.9 (a) Interpolated result with the thresholding method;(b)F-K spectrum of Fig.9a 图10 (a)重建结果与原始数据的误差;(b)图10(a)的F-K谱Fig.10 (a) Difference between the interpolated data and the original data;(b)F-K spectrum of Fig.10a 下面通过一个三维数据试验来进一步验证文章的结论。虽然对于三维数据也可以用二维变换对时间或频率切片执行,但是这样做没有利用数据在三维空间的连续性,因此论文采用三维变换为稀疏变换[32]。图11(a)为含噪声的三维数据,大小为,时间采样率为4毫秒,道间距为12.5米。图11(b)为图11(a)的采样,随机的采样50%道,图12(a)为基于本文的重建方法的结果,阈值经过了精心选择,该方法不仅重建了地震道,而且消除了随机噪声,提高了信噪比,图12(b)为原始数据和重建结果的误差,几乎不存在有效信号。 图11 (a)含噪声的三维数据体;(b)随机采样50%的结果Fig.11 (a)Noise contained 3D data;(b)50% randomly sampled result of Fig.11a 图12 (a)迭代阈值法重建的结果;(b)重建结果与图11(a)的误差Fig.12 (a)Interpolation result with the thresholding method;(b)the difference between Fig.12a and Fig.11b 文章对基于稀疏变换和矩阵完备理论的地震数据重建问题的数学模型和算法进行了归纳总结,给出了凸集投影算法的一种推导过程,证明凸集投影法是求解等式约束反演模型的方法,阐明了其不适合含噪声数据重建的原因。正则参数的选择是基于稀疏反演的含噪声数据重建的关键,文章介绍了几种正则参数的选择方法和原则,阐明了只有正则参数合适算法才能得到合适的解。最后用迭代阈值法求解含噪声数据重建试验证明正则参数选择的重要性。 对于反演问题,正则算子和正则参数是决定反演成败的关键,更多的研究应该集中于这两方面。目前正则参数一般由经验和尝试所得,这会耗费一定的时间,研究含噪声数据重建的自适应方法,在没有过多人为干预的情况下实现含噪声数据的重建和去噪具有重要意义。




2 数值模拟

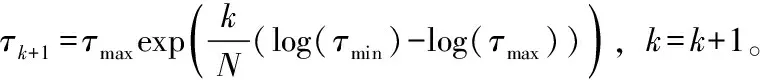










3 结论与讨论

