全球视野下京房“一日音差”发现的重大历史意义

喻 辉

“中国(律学)方法的简单性和准确性在东方没有被全面赏识，在西方一直被语言障碍遮蔽……从中国律学家的著作中，我们见证了在理论和实践之间，在一方面寻求绝对完美和另一方面接受常识性简便之间的卓越平衡。”(1)“The simplicity and accuracy of Chinese methods，not fully appreciated in the East，have been hidden from the West by the language barrier…In the work of Chinese acousticians we witness a remarkable balance between theory and practice，between the pursuit of absolute perfection on the one hand，and the acceptance of commonsense simplification on the other.”载Ernest G.McClain and Ming Shui Hung，“Chinese Cyclic Tunings in Late Antiquity”，Ethnomusicology，vol.23，no.2(May，1979)，p.20。(中文为本文作者翻译，以下同)。

欧内斯特·麦克莱恩(Ernest G.McClain)(2)欧内斯特·麦克莱恩(Ernest G.McClain，1918—2014)，原纽约市立大学布鲁克林学院教授，主要研究人类历史上宗教和哲学文献中隐含的古代音乐的数学原理。

一、“京房六十律”理论体系在当代中国音乐史研究中的评价问题

同明代朱载堉“十二平均律”计算方法的发现被认为是中华民族对人类科学和人文探索的重大贡献所不同的是(3)时任国家主席江泽民1997年在美国哈佛大学演讲中将朱载堉的发现与张衡地动仪的发明和祖冲之圆周率的发现并列为中华民族对世界作出过的独特贡献。见“江泽民主席在美国哈佛大学演讲”，《人民日报》1997年11月2日第一版。，学界对汉代“京房六十律”理论体系的评价一直众说纷纭，使其成为中国音乐史研究领域中最具争议的话题之一。很多学者认为汉代京房(前77—前37)对通过五十三次五度相生，生出距出发律黄钟非常接近的“色育”一律的发现具有正面意义，但很难理解为什么京房还要继续生律直到六十律。于是从五十三律到六十律的进一步连续生律一度被许多人认为是京房理论的一个负面包袱。另外一些学者则认为“京房六十律”没有任何实践意义，因为这个六十律没有在乐器上实现，京房也没有制造出演奏六十律的乐器。(4)京房认为“竹声不可度调”，曾制作过十三弦的“准”进行六十律的标记。但这个“准”作为一个声学实验的用具，并不是一个用来演奏的乐器。

目前看到的关于京房理论最早的负面评价可能来自王光祈先生，他认为京房认识到十二律黄钟不能还原的缺陷而自创新律，但其最终得出的计算结果仍未能求得黄钟，“这真是以五十步笑百步了……故我们计算京氏新律，最好推至五十三次为止”(5)王光祈：《东西乐制之研究》，见《王光祈音乐论著选集》(下册)，冯文慈、俞玉滋选注，北京：人民音乐出版社，1993年，第522页。。

杨荫浏先生认为“若说京房六十律能有什么作用的话，则它所起的，只能是消极的作用。那就是，它导向了脱离实际的、钻牛角尖式的乐律数字的玩弄。它导向了唯心的乐律神秘主义”(6)杨荫浏：《中国音乐史稿》(上册)，北京：人民音乐出版社，1981年，第132页。。前辈学者沈知白先生也认为京房的理论“在音乐上并没有实用的价值……他的目的不在于解决乐律本身所存在的问题。”(7)沈知白：《中国音乐史纲要》，上海：上海文艺出版社，1982年，第47—48页。

赵宋光先生在1964年编撰的一份内部资料《京房六十律与钱乐之三百六十律简明剖析》中对京房算到五十三律给予了正面的评价，但也认为其理论研究并无实际用处，认为“从数字内容方面来说，最初的五十三律构成了一个大致均匀的音阶，这五十三律音阶在律学史上有一定的地位，但对应用实践并无用处……京房和钱乐之的做法对后人是个教训，它表明谁要是死守三分损益法一直走下去，一定会钻进死胡同，远远脱离实践。”(8)赵宋光：《京房六十律与钱乐之三百六十律简明剖析》，中央音乐学院中国音乐研究所1964年印。

缪天瑞先生在其1983年出版《律学》(第二版)中认为“京房的律制还是有它的科学价值，这是主要的一面……这种复杂的律制应用起来十分困难，但可以在律学上作为科学实验之用”(9)缪天瑞：《律学》，北京：人民音乐出版社，1983年，第119—121页。。他同时又认为“但是京房为使律数与历数相结合，就凑成六十整数”。(10)同注⑨，第199页。

黄翔鹏先生在《中国大百科全书·音乐舞蹈卷》的“京房”词条中，对“京房六十律”给予了肯定的评价。他认为京房的贡献在于“提出了推演三分损益法而成的，扩大应用变律的‘六十律’学说，同时提出了否定管律、采用弦律的理论与方法……就西汉时先秦钟律的失传与京房变律限用三分损益法来说，六十律都不是单纯的因袭旧法，而是一种创造”(11)“京房”条目，《中国大百科全书·音乐舞蹈卷》，北京：中国大百科全书出版社，1992年，第318页。。

陈应时先生从20世纪80年代初开始通过发表一系列论文，提出应该全面正面评价“京房六十律”(12)陈应时：《为京房六十律申辩》，《艺苑》音乐版，1985年，第1期；《“京房六十律”再辩》，《黄钟》，2009年，第3期；《“京房六十律”三辩》，《黄钟》，2010年，第2期等。。在至关重要的为什么京房在通过五十三次生律得到非常接近出发律的“色育”一律后依然继续生到六十律这个问题上，陈先生认为京房从五十三律继续推演到六十律是有其理论意义和实际音乐需求的。他提出“京房六十律”的目的不仅仅在于解决“还原黄钟”的问题，而是要在六十律之内达到“还相为宫”。“但光有第五十四律色育律一个音，还成不了‘均’，所以必须再生六律，才能构成和黄钟均七律各相距‘一日’的色育均……六十律这个整数不是‘凑’的，而是为了切合理论上周而复始旋宫转调的实际需要”(13)陈应时：《为京房六十律申辩》，见《中国乐律学探微—陈应时音乐文集》，上海：上海音乐学院出版社，2004年，第462页。。美国学者麦克莱恩在1979年发表在《民族音乐学》期刊上的一篇文章中也认为京房的六十律实际上是5×12=60的结果，(14)“The sequence of fifths 2：3 and fourths 3：4 was sometimes extended to as many as 5×12=60 tones，”见Ernest G.McClain and Ming Shui Hung，“Chinese Cyclic Tunings in Late Antiquity”，Ethnomusicology，vol.23，no.2(May，1979)，p.205。这个观点同陈应时先生的观点不约而同。崔宪先生也认为“这六十律的最后七律，目的就是构成回到‘黄钟均’的七律。”(15)崔宪：《先秦乐律的历史流变》(上)，《黄钟》，1994年，第1期，第6页。

观照中西律学研究进程，笔者认为“京房六十律”是一个具有开创性思维的独特的律学理论体系，这个体系在律学史上最重要的成就是京房对他称之为“一日”的3.615音分音差的发现。这个音差的发现昭示了通过五十三次五度相生有可能回到出发律，这为包括后世的钱乐之以及西方17世纪的律学探索开启了新的方向。因此本文用京房“一日音差”的发现来代表“京房六十律”律学理论体系的创新。

“京房六十律”理论的出发点是五度相生法，其所涉及的主要音程距离都在自然音阶内。从古希腊和中国律学研究的相似性来看，自然音阶的构成具有跨文化的普遍声学理论意义。当我们将京房理论体系放到一个跨文化的背景下来审视时，我们会发现一些学术界以前没有能给予充分评价的新内容。我认为从中西律学史比较的角度来看，京房的“六十律”理论至少包含以下两点需要我们重新给予高度重视的历史成就。

1．京房是目前为止我们已知的人类历史上具有确凿可信文字记载的第一个对乐律学进行深入探索的科学实践者。京房所发现的“一日音差”是当时人类所知道的最小音差。

2．“京房六十律”的计算在生律五十三次时对“一日音差”的发现很可能启示了17世纪西方五十三平均律的探索。京房所进行的五十三次三分损益计算同后期在西方出现的“麦卡托循环”(Mercator Cycle)理论基础完全相同，但比麦卡托(Nicholas Mercator)(16)尼古拉斯·麦卡托(Nicholas Mercator，1620—1687)，原名尼古拉斯·考夫曼(Nicholas Kauffmann)。17世纪德国数学家，生于德国石勒苏益格—荷尔斯泰因州的尤廷(Eutin，Schleswig-Holstein，当时属于丹麦)。1632年进入罗斯托克大学(University of Rostock)学习，1641年获得学位。1642在该校哲学系任教。1648年至1654年在哥本哈根大学任教，在此期间他出版了大量关于球面三角、地理学和天文学的教科书。他最早在数学领域发现了级数，并在1668年出版的著作《对数术》(Logarithmotechnia)中描述了“自然对数”。、霍尔德(Williams Holder)(17)威廉·霍尔德(William Holder，1616-1698)，17世纪英国音乐理论家和牧师。早期曾就读于剑桥大学，1663年成为英国皇家学会会士。1687年被选为瑟菲尔德(Therfield)教区的牧师。他的一些音乐作品保存在大英图书馆中，编号为Harleian MSS 7338和7339 。据说他于1660年在布莱辛顿(Bletchingdon)教会了一个聋哑人亚历山大·波普尔姆(Alexander Popham)说话，但这个贡献到底属于他本人还是属于另外一个学者一直存在不同争议(见BBC相关报道http：//news.bbc.co.uk/2/hi/health/7511446.stm，最后访问：2021年3月1日)。他最著名的作品是1694年出版的音乐理论著作《论和声的自然基础和原理》(A Treatise of the Natural Grounds and Principles of Harmony)。和牛顿(Issac Newton，1643—1727)等西方科学家和音乐学家的理论探索早1700余年。“六十律”计算结果中的几个音程已经非常接近纯律音阶的音程，并很可能体现了春秋战国时期编钟上纯律使用的理论积淀。

二、京房“一日音差”与西方“麦卡托音差”的比较及其在世界律学史中的地位

中国的三分损益法和古希腊的毕达哥拉斯律之间在相当程度上具有同质性，两者的基本数理原则都是2 ∶3这个核心比例，其学理基础和结果是基本相同的。两者在西方被统一称之为毕达哥拉斯律或者循环律(cyclic tuning)。朱谦之先生认为因为古希腊的理论一直是使用弦长比而中国一直到京房才意识到管比的缺陷，因此推测古希腊的理论比中国更加成熟，并且京房的理论应该是受毕达哥拉斯理论的影响(18)朱谦之：《希腊与中国音乐之交流》，见《朱谦之文集》(第七卷)，福州：福建教育出版社，2002年，第281页。。但朱先生并没有拿出任何具体证据来支持这个推测。西方也有人认为在公元前两千年巴比伦时代的里拉琴就是用三分损益法进行调音的。(19)“‘the simple and easy method of the ancients，’have been documented as a basic Babylonian lyre tuning in the 2nd millennium B.C.(Kilmer 1976).”见Ernest G.McClain and Ming Shui Hung，“Chinese Cyclic Tunings in Late Antiquity”，Ethnomusicology，vol.23，no.2(May，1979)，p.222.转引Kilmer，Anne D.，Richard L.Crocker and Robert R.Brown，Sounds from Silence：Recent Discoveries in Ancient Near Eastern Music，Berkeley：Bit Enki Publications，1976。这就为五度律到底源自希腊还是中国的问题提供了进一步研究的余地。也有西方学者为了区别三分损益法存在着毕达哥拉斯律所没有的下生五度的生律现象，而用“上下生律法”(up and down method)来特指中国的三分损益法(20)见Fritz Kuttner，“Prince Chu Tsai-Yü′s Life and Work：A Re-Evaluation of His Contribution to Equal Temperament Theory”，Ethnomusicology，vol.19，no.2(May，1975)等文献。。从文献上看，中国最早出现三分损益法记载的《管子·地员篇》的真实成书年代和作者，我们现在还不能够完全确定。书中也没有明确说明是否为管子的发现，目前也没有任何对那个时代乐律探索人物的记载。在西方，“毕达哥拉斯律”也只是以毕达哥拉斯命名的一种调音办法，我们也不能最终确认是否由毕达哥拉斯本人所发现。现在一般被认为它是后世克罗狄斯·托勒密(Klaudius Ptolemaeus，约90—168)等人以“毕达哥拉斯”名字命名的一种律制，其出现的真实年代和发明人现在依然不清楚。托勒密在其著作中对毕达哥拉斯律的记载现在看来可能是西方最早的律学探索的记录。但托勒密出生在京房去世100多年以后，所以如果从存世的中外文献记载来看，京房是人类目前所知道的世界上最早有确定文字记载的律学现象的探索者。

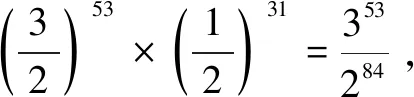
音差是在相同或者不同的自然音阶中主音持续移位后形成的微小的同音不同律的音程距离。它的发现反映了人类对自然声音现象的科学认识。虽然18世纪的西方科学家们经过探索又重新发现了这个3.615音分的音差，并进行了重新命名，但这丝毫不影响京房早于西方1700余年发现人类当时所知的最小音差的事实。接下来需要回答的问题是，京房“一日音差”的发现对音乐实践的意义是什么？我认为这个问题可以从两个方面来认识：

第一，“一日音差”的发现为沟通五度相生律、纯律和平均律提供了一个重要的理论思路。也就是说利用五度相生的生律法也可以生成近似纯律和平均律音阶。其方法是找到一个可以成为三种律之间公约数的音程。从表1中我们可以看到，京房在计算六十律的实践中已经计算出了非常接近纯律的音程。同五十三平均律一样，他的六十律中包含了许多纯律中的自然律音程。我们从先秦曾侯乙编钟的实物和古琴的实践中已经知道纯律的应用在中国古代的音乐实践中是一直存在的，但中国古代长期以来没有一个系统的纯律理论体系。陈应时先生曾通过对沈括“自然之节”和朱熹《琴律说》中提到的“折纸法”等理论的研究证明中国古代纯律理论的存在(22)陈应时：《论证中国古代的纯律理论》，《中央音乐学院学报》，1983年，第1期，第34—39页。，但沈括和朱熹的理论都出现在“京房六十律”理论发现1000余年以后。因此先秦变律的音乐实践一直没有在中国古代乐律学体系中留下系统的理论痕迹。从“京房六十律”的计算中我们发现了纯律音程的存在。因此，京房通过三分损益法求得其他变律的计算是一次契合中国音乐实践的宝贵的律学探索。

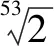
综上所述，我们可以看到体现“京房六十律”理论核心内容的音乐实践是存在的，只是出现在很多年以后。也就是说他的理论远远早于人类的音乐实践，因此其实践意义是不能被否定的。我们更不能因为错误地认为“京房六十律”没有能在当时的乐器上进行演奏，进而否定其整个理论体系的科学和历史价值。

三、京房、麦卡托、霍尔德和牛顿理论的同质性和共同的数理基础

到了17世纪，欧洲漫长的中世纪结束，文艺复兴带来了人们的觉醒，欧洲的科学和艺术走向空前繁荣。同“京房六十律”理论基础基本相同的五十三平均律和“麦卡托循环”理论在欧洲学术界又重新引起了人们的兴趣，并进一步体系化。这个理论在欧洲的出现主要归功于三位科学家。第一位是在当时丹麦出生的数学家和天文学家尼古拉斯·麦卡托，第二位是英国数学家威廉·霍尔德，第三位是大家所熟知的著名科学家艾萨克·牛顿。麦卡托和牛顿的研究成果目前只存在于他们没有发表的手稿之中。霍尔德在他1694年公开出版的著名音乐理论著作《论和声的自然基础和原理》一书中阐述了麦卡托理论。这也是世界上最早阐述五十三平均律理论的英文文献。

牛顿虽然没有公开出版过音乐方面的专著，但他对音乐和声学问题进行过深入的研究。他在音乐理论方面的探索，主要留存在他未出版的两份手稿中。一份是题为《论音乐》(OfMusick)的文章。在这份手稿中，牛顿尝试使用各种方法把一个八度分成更小的音程。(28)Peter Pesic，“Issac Newton and the Mystery of the Major Sixth：A Transcription of His Manuscript‘Of Musick’with Commentary”，Interdisciplinary Science Reviews，31(2006)，pp.291-306.另一份是包含了很多律学计算的手稿文件，里面有一份文件涉及到对数的使用。第二份手稿则在纸面上留下了1665年11月20日的写作日期(29)Benjamin Wardhaugh，Music，Experiment and Mathematics in England，1653-1705，London：Routledge，2008，p.53.。在这些计算手稿中有两幅牛顿手绘的关于五十三次五度循环的草图。这两幅草图在中心区外用五个圈代表五个重要的音阶，并用唱名法来标注音级的名称。在圈的外侧标注了将一个八度分成五十三份以后每个音程的大概距离和位置。第一幅草图中圆圈的外围有两套数字，标记了把一个八度分别分成五十三份后的基本位置(30)同注，p.55.。第二幅草图只标明了五十三律，非常明确地将53标记在起点位置稍稍超过一点的地方，这同京房的五十三律比出发律超出一个3.615音分的“一日音差”的计算结果非常相似。

(剑桥大学图书馆，编号：MS 4000，fol.109r)(31)Benjamin Wardhaugh，Music，Experiment and Mathematics in England，1653-1705，London：Routledge，2008，p.53.

(剑桥大学图书馆，编号：MS 4000，fols 109r-9v)(32)牛顿手稿中共留下两幅草图，本杰明·沃德豪(Benjamin Wardhaugh)在书中只引用了第一幅草图，但给出了第二幅草图的剑桥大学图书馆编号(p.55)。美国哈佛大学音乐理论家马克·林德利(Mark Lindley)和英国音乐理论家罗纳德·特纳-史密斯(Ronald Turner-Smith)合作在美国音乐理论学会(Society for Music Theory)的在线出版物Music Theory Online[ISSN：1067-3040]1993年第三期上发表的《一个音阶数学模式的代数方法》(An Algebraic Approach to Mathematical Models of Scales)一文中引用了本文图2，即牛顿的第二幅草图。

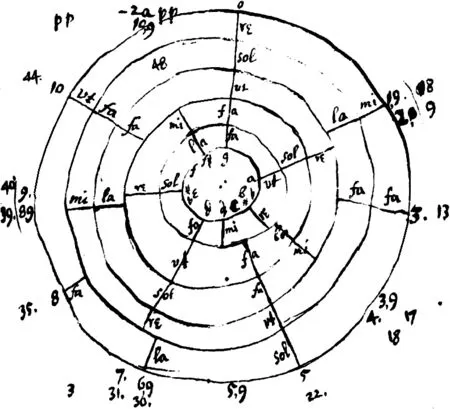
图1.牛顿关于音高循环思考的第一幅草图 图2.牛顿关于音高循环思考的第二幅草图

但这只是我们目前所知道的关于牛顿在五十三律问题上研究的所有纸面档案，它反映的是牛顿在这个问题上的基本思路。至于他在这个五十三律问题上是否还有更加深入的理论思索和文字表述，尚有待于科学史学家和音乐史学家们的进一步的共同努力。

麦卡托的律学研究主要是通过威廉·霍尔德的著作介绍出去的。霍尔德曾经是一位神职人员和著名的音乐理论家。他1694年出版的著名音乐理论著作《论和声的自然基础和原理》，是他一生中最主要的音乐学术贡献。霍尔德在书中阐述了麦卡托在一篇手稿中所提倡的五十三平均律，这个理论同京房的计算方法非常接近，所以麦卡托理论后来在西方也就因此被称之为“麦卡托循环”。美国著名的律学史研究专家默雷·巴伯(Murray Barbour)在1951年出版的重要律学专著《律学史》(Tuning and Temperament：A Historical Survey)中引用了霍尔德的原话来解释麦卡托的理论，他提到：

霍尔德认为，尼古拉斯·麦卡托“推算出了一个精妙的发明，发现并使用了最小的通用尺度测量所有的谐音音程，虽然不是绝对完美，但非常接近”。这就是53个音差的分割。在霍尔德的叙述中，并没有证据说明麦卡托准备把这个系统应用在某件乐器上。它仅仅将被作为一个“通用尺度”。(34)“According to Holder，Nicholas Mercator had‘deduced an ingenious invention of finding and applying a least Common Measure to all Harmonic Intervals，not precisely perfect，but very near it.’This was the division into 53 commas.There is no evidence，in Holder’s account，that Mercator intended this system to be used on an instrument.It was to be merely a‘Common Measure’.”见J.Murray Barbour，Tuning and Temperament：A Historical Survey，East Lansing：Michigan State University，1951，p.125。

霍尔德的这段话后来也被其他学者广泛引用，对麦卡托理论的传播产生了久远的影响。同时，也正是因为霍尔德这段话的推崇，五十三平均律每个音程之间的距离也通常被冠以“霍尔德音差”(Holdrian Comma)的名称。

从巴伯对霍尔德著作的引用中，可以看出霍尔德在麦卡托理论的传播和建立过程中起到至关重要的作用。为了进一步研究霍尔德这段阐述的文字背景，本人经过多方努力得到了1731年出版的第三版《论和声的自然基础和原理》一书，并进行了详细的分析。

图3.霍尔德《论和声的自然基础和原理》第三版封面

该书的第五章主要阐述有关声音的比例(proportion)问题。霍尔德对各种音程关系背后所蕴含的数字比例进行了详细的阐述。巴伯在介绍“麦卡托循环”时所引用的霍尔德的一段话也出自这一章。但经过比较笔者发现巴伯所引用的原文并不完整。为了全面了解涉及五十三平均律理论起源的这段关键文字，笔者将原话的全段完整翻译如下：

图4.《论和声的自然基础和原理》中有关麦卡托五十三平均律内容的原稿

梅森通过他的计算在一个八度里面发现了58 1/4，或许更多的音差。但是后来一个谦逊、学问渊博、思路清晰的人——数学家尼古拉斯·麦卡托在他的一份手稿里对这个问题做出这样一个评价：In solvendo hoc Problemate aberrat Mersennus(拉丁语：不能用修改梅森的方法来解决这个问题)。他使用对数的方法发现了稍多于55个(音差)，并在这个基础上推演出他的一个精妙的发现作为衡量所有谐音音程的最小的通用尺度，虽然不是绝对完美，但非常接近。

我们发现在巴伯的引用中，关于55个音差说法的前几句话都被省去，这使得霍尔德的整个阐述变得难以理解。于是巴伯只能自己又添加上一句“这就是53个音差的分割”以避过文中所提到的五十五律的文字。但如果我们仔细研读上下文，实际上霍尔德在紧接着这段文字的下一段话为我们理解这一段话的内容提供一个清楚的注解：

设想一个音差是一个八度的1/53。为了更好的包含而不是根据真正的1/53分割，他称这个1/53为人工音差，虽然不是很精确，但同真正的自然音差还相差一个1/20音差，和(35)笔者认为原文有误。见后文详述。一个八度音程的1/1000(是一种难以察觉的差别)。这样一个八度内的音差可以根据下面的表格来进行测量。这里面你可以加上或者减去两三个或者更多音差，看它们是如何构成这些音程的。

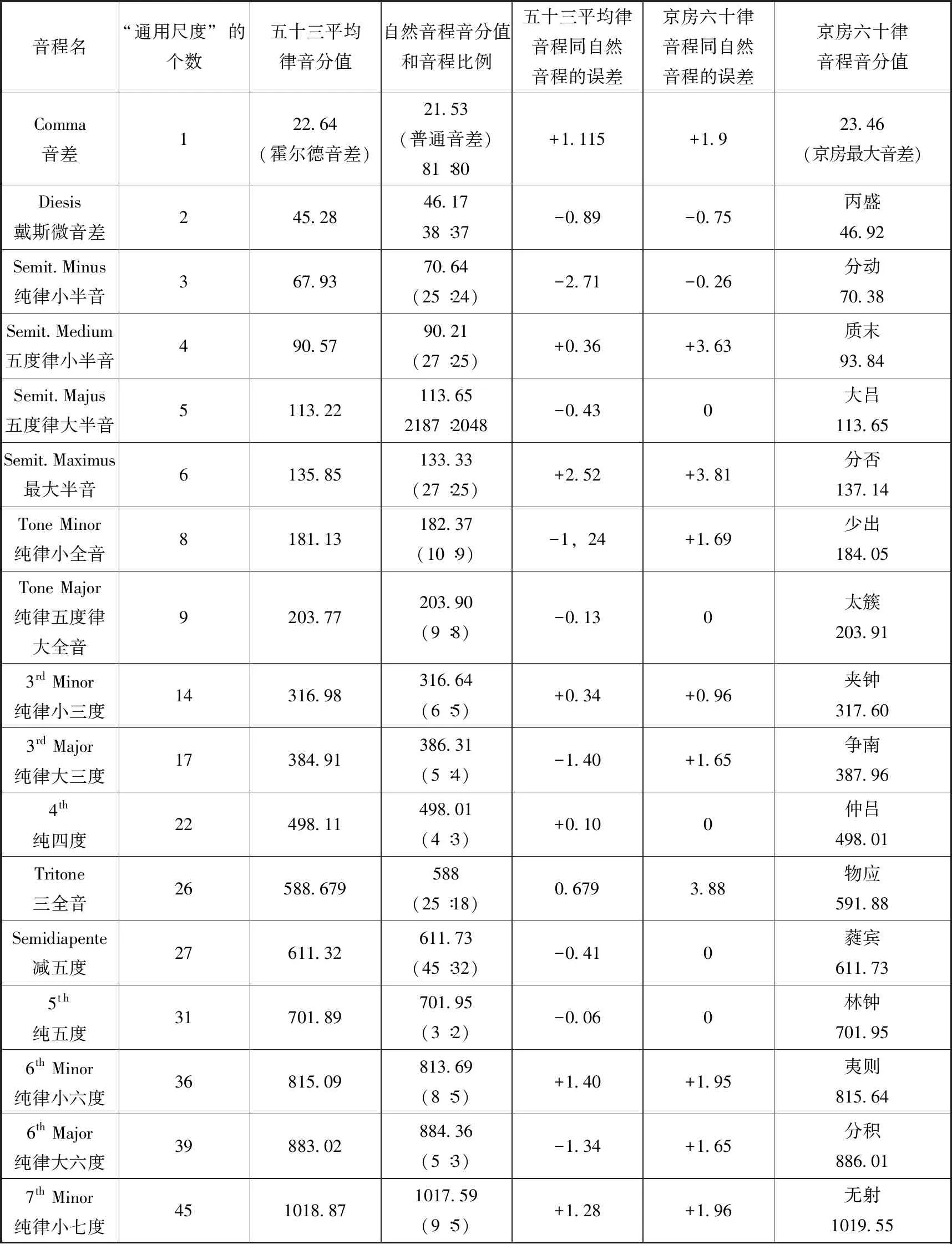
表1.霍尔德《论和声的自然基础和原理》第三版第80页说明麦卡托五十三平均律理论中“通用尺度”的表格翻译以及和京房“六十律”中相应音程的比较(两者同自然音程之间的误差)

续表

表1中左边的两列为霍尔德原文中的列表，右面的五列是笔者为方便读者将麦卡托律和京房六十律同自然律音程之间的误差进行比较而加上的数据，音分数精确到小数点后两位数。

从霍尔德这段原文中，我们可以发现几个值得重视的事实：

1.西方所谓“麦卡托循环”的出处实际上是来自霍尔德的上述文字，而不是麦卡托本人的论述。霍尔德在文中自称看到过麦卡托提交给朋友的手稿，并把手稿中的内容进行转述解释，于是这个22.64音分的音程后来也就被称之为“霍尔德音差”。

2.霍尔德所说的“通用尺度”(Common Measure)可以测量所有自然音程的这句话，在他下文的表格(本文表1)中得到注解。那就是将一个八度分割为53个平均音差后的22.64音分。以这个后来被称之为霍尔德音差的22.64音分为通用尺度单位，基本上可以度量五度律和纯律中的全部主要特性音程。从表1可以看到，两者之间实际差距很小。也就是说几乎所有五度律和纯律的音程都可以是霍尔德音差的倍数，因此霍尔德音差实际上构成了沟通五度律和纯律中的自然音程的一个公约数。

3.我们在表1中将京房“六十律”中相应的音程放到五十三平均律中进行相互比较后发现，五十三平均律中很多音程其实在京房六十律中已经存在。表1中的数字显示，霍尔德在文中所阐释的五十三平均律的音程完全可以用京房“六十律”中的律数来实现。京房通过六十次五度相生，不仅仅在生律五十三次时找到当时人类所发现的最小音差，而且在他的计算结果中已经出现了西方后期才提出的纯律理论中的纯律特性音程。如，从京房计算出的六十律中我们可以构成黄钟为宫的以下纯律大音阶：

表2.京房六十律中的纯律音阶

可以看到，无论是从麦卡托的五十三平均律还是从“京房六十律”中提取的纯律音程同自然纯律特性音程的差别都不超过2音分，这是人类耳朵基本无法辨别的音差。

4.霍尔德著作的第一版出版于1694年。笔者手上的这本是出版于1731年的第三版。因为时间非常久远，有些语言不是非常连贯。从英语发展史上来看，1500—1700年一般被英语语言学家们认为是一个早期现代英语的时代(Early Modern English)，在此之后则是一个现代英语时代。该书的出版处于英语语言从早期现代英语向现代英语发展的转折时期，因此某些语言和标点符号使用上可能不完全符合我们目前使用的现代英语用法。如果仅从字面上理解，有些说法甚至会影响到我们对霍尔德思想的正确把握。比如：

(1)有些用词如Diepason(和谐八度)，Diepenate(五度)等，现代学者已经很少使用了。

(2)书中存在一些错字，甚至包括一些关键字。比如该书第79页上介绍麦卡托理论的时候。霍尔德开始说是五十五律，而不是五十三律。然而，紧接着后面又开始介绍了五十三律。因此这个五十三和五十五的区别导致了一些混乱，甚至有人认为除了五十三平均律之外还存在着另外一种五十五平均律(36)维基百科条目：https：//en.wikipedia.org/wiki/Holdrian_comma#Mercator's_comma_and_the_Holdrian_comma(最后访问：2021年4月1日)。巴伯在引用这段话的时候，因为很难解释五十五律的情况，就只好从这一句话后面开始引用，然后再自己加上一句解释，说所指的就是五十三律。笔者认为，这个“五十五”实际上就是“五十三”的笔误。理由有两点：第一，是在这句话以后，作者没有做任何铺垫，直接解释了五十三平均律的用处。并且，只有使用五十三平均律的22.64音分作为一个计算单位才可以同他后面所做的音程表进行对应。笔者按照霍尔德后面的音程表，使用五十五平均律的音程重新算了一遍，结果是五十五平均律的基本音差21.818音分所算出来的音程同后面列表中的自然音程基本构不成倍数单位，不能作为一个衡量自然音程的“通用尺度”。第二，在后面列表的两栏应该完全相同的标题中，一个写成了“0/54”，另一个写成“0/53”。根据表中的内容来看，显然后者才是正确的。既然霍尔德书中确实存在着其他方面的笔误，这个“五十五”也就可能是“五十三”的笔误，因此麦卡托实际上可能并没有提出所谓的五十五平均律理论。

(3)行文中的一些用法可能同现代英语用法也有些区别。比如文中有一句话：

他叫做“人工音差”，虽然同真正的自然音差不完全一样，还相差一个1/20音差，和(原文为and——译者注)一个八度音程的1/1000。(37)“which he calls an Artificial Comma，not exact，but differing from the true Natural Comma about 1/20 part of a Comma，and 1/1000 of Diapason.”见Holder，William，A Treatise on the Natural Grounds and Principles of Harmony，London：Printed by W.Pearson，1731，pp.79-80。

这段话原英文里有一个“and”。如果按照通常英语的用法把“and”当作“和”来理解，其意思就变成了一个自然音差加上它的1/20，再加上一个八度的1/1000。那么这个音差就变成了21.526+21.526/20+1200/1000=21.526+1.08+1.2=23.81。这个音差同五十三平均律的22.64音差的差别是1.37音分，显然太大，构不成平均律。但如果把这个and理解成“或”，也就是说他使用这个and，表明是有两种可能，那么整个内容就比较容易理解了。因为无论是21.526+1.08=22.606还是21.526+1.2=22.726，距离22.64音分都是在0.04音差左右，基本可以看成是相同的音差。

四、京房“一日音差”理论同欧洲17世纪五十三平均律理论的关联性

时至今日，许多西方音乐学家依然没有意识到五十三平均律的出现同中国古代京房的理论体系之间存在的直接关系。如《新格罗夫音乐与音乐家辞典》中认为：

在17世纪，受中庸全音律的影响，将八度分成平均微分音的相关方法在对数的帮助下出现了……加利(Gallé)大概在1637年研究出一种53个音级的纯律音程，这同牛顿于1665年和麦卡托于1670年代所推崇的很类似。(38)“For various shades of mean-tone the corresponding schemes of dividing the octave into equal microtones were worked out，with the aid of logarithms，during the 17th century…By 1637 Gallé had properly reckoned the intervals of just intonation in terms of the 53-part division，similarly favoured by Isaac Newton in 1665 and Nicolas Mercator in the 1670s.”见“Temperaments”，in Stanley Sadie and John Tyrrell ed.，New Grove Dictionary of Music and Musicians，2001，vol.25，p.255。

在17世纪，尼古拉斯·麦卡托提出把一个八度平均分成五十三份，马林·梅森(Marin Mersenne)和克里斯蒂安·惠更斯(Christiaan Huygens)提出分成三十一份。这些建议分别属于纯律和中庸全音律。(39)“In the 17th century Nicolaus Mercator suggested 53 equal divisions of the octave and Marin Mersenne and Christiaan Huygens 31；these result virtually in just intonation and mean-tone temperament respectively.”见“microtonal instrument”，in Stanley Sadie and John Tyrrell ed.，New Grove Dictionary of Music and Musicians，2001，vol，16，p.618。

美国微分音作曲家温蒂·卡洛斯甚至认为：

毕达哥拉斯一个名叫菲洛劳斯(Philolaus)的学生用文字描述了一个构成音程的方法。这个方法用人们所知的麦卡托循环直接导致一个53音差大小尺度的测量表。(40)“A student of Pythagorus named Philolaus wrote a description of a method for constructing intervals which leads directly to a measuring scale of 53 comma-sized steps，in which form it is known as Mercator's cycle.”见Wendy Carlos，“Tuning：At the Crossroads”，Computer Music Journal，vol.11，no.1(Spring，1987)，p.39。

但前文对有关五十三平均律理论关键原文的分析可以从两个方面说明麦卡托五十三平均律理论同京房的“六十律”计算之间在学理上存在着密切的关联：

1.霍尔德在著作中竭力强调对数的用处，无论是在他提到梅森的58 1/4的八度划分(41)Holder，William，A Treatise on the Natural Grounds and Principles of Harmony，London：Printed by W.Pearson，1731，p.79.还是麦卡托的五十三律时，都提到他们是使用了对数计算才得到了结果。在霍尔德出版此书的时候，对数已经开始广为人知。荷兰工程师西蒙·史蒂芬(Simon Stevin)关于十二平均律理论的论著已经写成。无论是五十九平均律、五十五平均律还是五十三平均律都是由于对数的使用才帮助了人们更明了地理解了平均律的计算和理论。但霍尔德的整个著作只是在提到麦卡托理论的时候才出现过对数(logarithm)一词。全书讨论的全部是关于和声的简单数学比例，也就是不需要开方和对数运算的自然律(五度律和纯律)的振动比例和弦长比例的问题。同时在霍尔德的文字中，我们可以看到五十三平均律的计算与五度相生的关系是非常密切的。如，在紧接上述引文后面的文字中，霍尔德直接开宗明义地说：

这里我想告诉读者的是，你用大数值和小数值进行比较，或者是用小数值和大数值比较，就是说3比2，或者2比3，无论你把谁放在前面都是没有区别的。因为在和声中弦长比和震动比是相对的，或者说是可互换的。(42)“Here I may advertise the Reader，that it is indifferent whether you compare the greater Term of an Harmonic Ration to the less，or the less to the greater；i.e.whether of them you place as Antecedent，e.gr：3 to 2，or 2 to 3；because in Harmonies the Proportions of Lengths of Chords，and of their Vibrations，are reciprocal or counter-chang′d.”见William Holder,A Treatise on the Natural Grounds and Principles of Harmony,London:Printed by W.Pearson,1731，pp.80-81。

去发现比例的比例……如果对八度和五度的大小进行比较，那就是0.301030比0.176091，我说的是八度里面的五度(或者说1/2比例中的1/3)的比例是53比31。(44)“to find the ratio of ratios…If the sizes of the octave and fifth are compared，that is 0.301030 and 0.176091，I say that the octave holds to the fifth(or the ratio 1/2 holds to 1/3)the ratio 53 to 31.”见Peter Pesic，“Issac Newton and the Mystery of the Major Sixth：A Transcription of His Manuscript‘Of Musick’with Commentary”，Interdisciplinary Science Reviews，31(2006)，p.51。

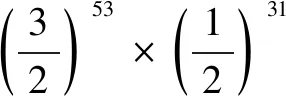
综上所述，我们可以发现京房和麦卡托两个相距1700余年，出现在地球两端的理论实际上是基于一个完全相同的数学公式。接下来的问题是“京房六十律”理论有没有影响过西方17世纪的麦卡托、霍尔德和牛顿等人，也就是说在麦卡托之前京房的理论和计算方法到底有没有传播到欧洲。

从本人目前所掌握的中外文文献中，还没有发现霍尔德和麦卡托等人在五十三律的研究过程中提到过中国和京房。也没有发现京房的研究在17世纪以前就被介绍到西方的确凿文字证据。甚至亥姆霍兹在《论音的感觉作为音乐理论的一个生理基础》(OntheSensationsofToneasaPhysiologicalBasisfortheTheoryofMusic)一书中提到麦卡托的五十三次循环的理论和计算时，也只是认为同毕达哥拉斯律极为相近，并没有提到过京房。虽然该书的翻译者埃利斯在书的前言和译者附录里提到过中国以及法国传教士钱德明对五度相生律理论的介绍，但也没有提到京房和他的“六十律”理论。(45)Hermann Ludwig Ferdinand von Helmholtz，Alexander John Ellis(Eng.tran.)，On the Sensations of Tone as a Physiological Basis for the Theory of Music，London：Longmans，Green and Co.，1875.译者在该书的第713页中介绍簧片乐器时引用了钱德明著作中关于十二律的有关论述。

目前所知道的在西方文献中对京房理论最早的介绍是法国人库朗(Maurice Courant)于1913年出版的《音乐百科全书和音乐学院词典》。巴伯的律学史著作中对京房的介绍也是引自这本书。(46)Maurice Courant，“Chine et Corée”，Encyclopédie de la musique et dictionnaire du conservatoire (Paris，1913)，part 1，vol.1，p.88.转引自J.Murray Barbour，Tuning and Temperament：A Historical Survey，East Lansing：Michigan State University，1951，p.124。他提到：

根据库朗(的介绍)，中国早期最卓越的理论家京房计算出了六十律的精确比例，也就是说他把毕达哥拉斯系统推进到60个音。这些结果被卒于公元306年的司马彪所发表。京房观察到第五十四律同第一律几乎相同。库朗的数字是第一律为177，147，第五十四律为176，777。(47)“One of the most remarkable of the early Chinese theorists was King Fang，who according to Courant，‘calculated exactly the proportional numbers to 60 lü，’that is，he extended the Pythagorean system to 60 notes.There results were published by Seu-ma Pyeou，who died in 306 A.D.King Fang observed that the 54th note was almost identical with the first note.Courant’s figures are 177，147 for the first；176，777 for the 54th.”见J.Murray Barbour，Tuning and Temperament：A Historical Survey，East Lansing：Michigan State University，1951，p.124。

巴伯在紧接着的文字中却又认为：

欧洲17世纪理论家肯定提到过中国系统的包括梅森(Mersenne)和基歇尔(Kircher)，田中正平(Tanaka)在这个联系中提到过基歇尔的名字，这和他的大多数同代人不同，他们把这个系统归功于麦卡托。(48)“Seventeenth century European theorists who referred definitely to this system include Mersenne and Kircher，Tanaka mentioned Kircher’s name in this connection，thus differing from the majority of his contemporaries，who ascribed the system to Mercator.”同注，pp.124-125。

但巴伯却没有在书中为他这个新颖的说法提供任何注释。笔者也尝试从其他文献中寻找梅森提到过的五十三平均律同中国有关的具体佐证，但均没有成功。

当然，如果今后的文献发现能够证明巴伯所说的梅森和基歇尔曾经提到过中国，那么我们就可以进一步确认17世纪西方对“麦卡特循环”理论的探索是直接受到了中国西汉时期京房律学研究的影响，甚至是照搬了京房的研究成果。然而，即使目前尚未找到这样的证据，根据目前的资料，我们依然可以断言，以京房“一日音差”的发现为标志的中国律学理论在1700余年以后的西方又被以另外一种形式重新发现并命名。由于两者基于相同的数字方法和表达公式，他们之间存在着继承和发扬关系的可能。但即使最终不能证明两者之间存在着直接联系，我们依然可以从中发现中华民族的伟大智慧和中国古代文明对世界文明的又一个重要贡献，这个贡献比西方文明在律学研究领域的同样发现早1700余年。

结 论

京房作为目前有确切文字记载的最早的律学探索者，他所发现的“一日音差”为当时世界上所知的最小音差。京房的发现比后来在西方被称之为“麦卡托音差”的出现早1700余年。京房用三分损益法计算到五十三次时所发现的这个音差，后来又在西方被牛顿、麦卡托和霍尔德等人重新研究，并很可能启发了麦卡托的五十三平均律理论的提出，因为两者是基于一个完全相同的数学公式。17世纪欧洲的数学家和音乐学家之所以发现“53”这个数字非常奇妙和重要，是因为将一个八度平均分为五十三份以后，会产生一个“通用尺度”。而这个尺度，可以大致用来衡量并产生我们目前已知的三分损益律、纯律和十二平均律。这个律学研究领域里划时代的重要概念，在中国音乐实践中的应用不迟于先秦时期编钟等乐器上变律的使用，理论上肇始于西汉时期伟大的乐律学家、易学家和哲学家京房通过“京房六十律”理论体系的探索对“一日音差”声学现象的发现。

京房的发现为后期纯律理论和平均律理论的出现提供了一个新的思路。那就是利用三分损益的生律方法不仅可以生出五度律，也可以生出接近纯律和平均律的音阶，并在实践上成为朱载堉十二平均律发现的主要计算方法之一。如果说十二平均律计算方法的发现在西方为键盘乐器的使用提供了便利，并推动了西方调性音乐的发展，那么五十三律理论的出现就为五度律、纯律和平均律理论在生律方法方面的沟通打开了一扇窗户，找到了三种律制之间可以使用相同生律方法的量化依据。十二平均律的发现没有终结律学的探索过程，律学研究也不以十二平均律的发现为终点。西方对京房理论体系的再发现(或再继承)是在十二平均律理论已经被发现并被实践的17世纪。这一事实充分说明了京房的律学理论是人类艺术和科学探索史上具有特殊意义的重大贡献。京房理论体系所代表的中国乐律学研究的高度智慧是中华古代文明在音乐学研究领域里早于西方1700余年的一座高峰，它不应该被具有同样伟大意义的朱载堉十二平均律理论的发现遮挡其更加古老的辉煌和历史价值。

西方学者李约瑟(Joseph Needham，1900—1995)曾经提出过一个著名的“李约瑟之问”，那就是“为什么现代科学、关于自然的数学化假设连同它所蕴含的所有先进技术，只会在伽利略时代(49)伽利略·伽利雷(Galileo di Vincenzo Bonaulti de Galilei)生于1564年2月15日，卒于1642年1月8日。西方关于“麦卡托循环”和五十三律的研究全部出现在李约瑟所说的伽利略后期，也就是欧洲文艺复兴时期。笔者认为这是一个值得音乐史学界和科学史学界共同进行探讨的一个非常有意思的文化现象。的西方才迅速崛起？……为什么现代科学只在欧洲而没有在中国(或印度)文明中得到发展？”(50)“Why did modern science，the mathematization of hypotheses about Nature，with all its implications for advanced technology，take its meteoric rise only in the West at the time of Galileo？…why modern science had not developed in Chinese civilization(or Indian)but only in Europe？”见Joseph Needham，The Grand Titration：Science and Society in East and West，Toronto：University of Toronto Press，1969，p.16。。之所以提出这个问题，是因为李约瑟认为“在公元前1世纪到公元15世纪，在将人类关于自然的知识应用于人类的实际需要上，中国文明比西方文明有效率得多。”(51)“between the first century B.C.and the fifteenth century A.D.，Chinese civilization was much more efficient than occidental in applying human natural knowledge to practical human needs.”同注，p.190。在中国音乐史研究领域里，笔者注意到一个非常有意思的现象，那就是在李约瑟所说的“有效率”的中国历史区间的前端出现了京房“一日音差”的发现这样划时代的研究，后端出现了一直被中国人引以为自豪的朱载堉十二平均律计算方法的发现。在朱载堉十二平均律发现的同期，西方也出现了西蒙·史蒂芬非常相似的研究，但京房的研究早于西方千余年的事实是可以断定的，因为同样的研究的确出现在西方的“伽利略时代”。在李约瑟所说的这个1700年左右的历史长河中，中国的音乐研究是否在“将人类关于自然的知识应用于人类的实际需要”上比西方有效率的多，还需要我们进一步研究和论证。关于这个阶段后期的朱载堉律学研究与中国音乐实践之间关系的问题，已经有不少同仁提出了自己的见解。但我们目前所看到的京房理论体系的实践大多出现在阿拉伯和西方世界。期望音乐学家和科学史学家们在这个问题上持续深入的探索，可以进一步揭示京房理论体系对西方“伽利略时代”和后期的律学研究以及对中国音乐实践更直接和更深入的影响。

本文为2019年10月31日至11月2日在马来西亚博塔拉大学(UPM)举办的以“音乐与宇宙”(Music and Cosmos)为主题的“第12届国际音乐研究论坛”(The 12th International Colloquium for Music Research)上以英文发表的主旨演讲(keynote speech)的中文翻译稿。主旨演讲的英文题目为 “Jing Fang’s Study of Organized Musical Pitches and His Contribution to Human Understandings of the Acoustic Cosmos”(京房音律组织的研究及其对人类声学宇宙探索的贡献)。