一种临近空间飞行器动态拖尾星图复原方法
孙洪驰,穆荣军,刘丽丽,崔乃刚
(哈尔滨工业大学 航天学院,哈尔滨 150001)
临近空间高超速飞行器飞行速度极快,姿态误差会对位置精度造成很大影响[1-3]。天文导航可以达到很高的姿态精度[4],引入天文导航对临近空间飞行器的姿态进行修正有助于提高飞行器的长航时精度保持能力,同时可以辅助修正惯导陀螺零偏,有效提高导航精度[5,6]。临近空间环境下天文导航面临的主要问题是飞行器大姿态机动时导致的星点拖尾[7]。星点拖尾会导致星点成像时能量分布发散,增加了星点提取的难度,甚至会导致导航算法失效[8]。
针对星图拖尾有两种解决方式:一是通过机械结构使曝光过程中的光学系统和被摄目标保持相对静止,从硬件层面抑制拖尾的产生[9]。但这种方法存在成本较高、结构复杂、体积大等问题,难以在临近空间飞行器上应用。第二种方法是通过图像复原算法来对拖尾图像进行复原,这种方法具有成本低、无需额外配置硬件、应用灵活等优点,适用于临近空间飞行器[10]。
文献[11]通过预测星点质心与提取星点质心之差,实现星敏感器动态误差补偿,但该方法对光轴方向动态误差分量的观测敏感性弱于其他分量;文献[12]提出一种基于维纳滤波的拖尾星图处理方法,但并没有考虑光轴方向角速度的影响,且对于拖尾参数的获取没有提出较为可行的方案。文献[13]利用局部直方图Gauss 拟合法估计背景参数,通过亚采样方法对目标进行增强,采用四邻域滤波对图像进行修复,算法复杂度较高,不利于提高算法的快速性。
本文以计算量较小的维纳滤波为基础,引入IMU量测数据构建图像复原函数,采用图像分割的方法对拖尾星图进行分布式处理,设计出一种计算量小、精度高、实用性强的拖尾星图复原方法。
1 图像分割分布式动态拖尾图像复原算法
动态环境下会造成星敏感器拍摄的图像出现拖尾现象,采用维纳滤波的方法可以实现动态拖尾图像的复原,但传统的处理方法只能对非光轴角速度引起的拖尾进行有效复原。这是因为维纳滤波主要用于民用相机中,日常使用时不会出现绕光轴方向的转动,故传统的处理方法是对整幅图像进行一次性集中复原。而在天文导航中,星敏感器绕任何方向的姿态机动都是可能出现的,本文对此提出一种图像分割分布式拖尾图像复原算法,通过图像分割对不同图像区域的星点进行分布式维纳滤波,可完全适应三轴角速度变化。
1.1 基于维纳滤波的拖尾图像处理方法

不考虑绕光轴的角速度时,一幅星图中的所有星点拖尾方向和大小均是一致的。在时域内,拖尾图像相当于原图像与退化函数的卷积,理想情况下图像的退化过程如下
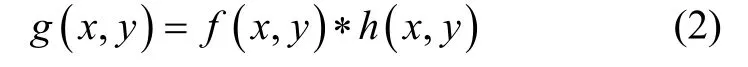
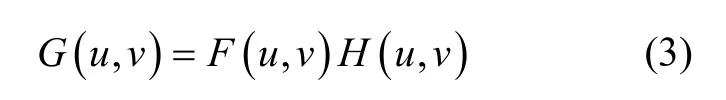
显然,有
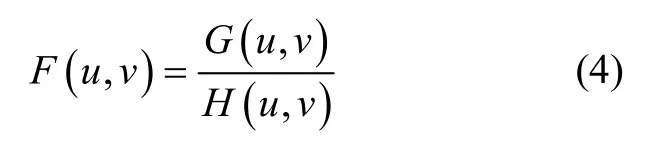
这一过程称为逆滤波,但在实际中退化图像除了受退化函数影响外还受到噪声影响,实际退化过程如图1所示。

图1 图像运动模糊的退化过程Fig.1 Degradation process of image motion blur
时域下退化过程如下:

这时需要采用维纳滤波进行复原,维纳滤波建立在认为图像和噪声是随机过程的基础之上,可使复原图像与原始图像的均方误差最小。频域中维纳滤波的表达式为:
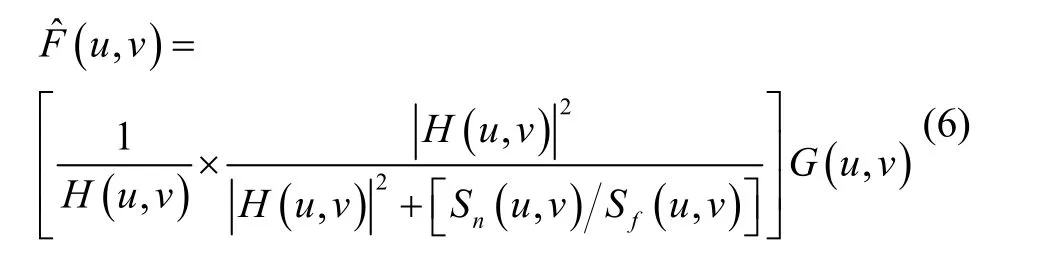
1.2 基于IMU 辅助的分布式拖尾星图复原方法
当存在绕光轴方向的角速度时,如图2所示,星图不同位置星点拖尾方向是不一致的,这时需要针对不同区域的星点进行分布式处理而不是对整幅图像进行维纳滤波复原。
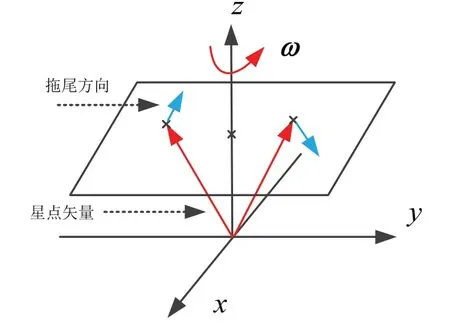
图2 星图拖尾效应原理示意图Fig.2 Schematic diagram of star map tailing effect
为提高计算效率,本文采用IMU 测量参数辅助构建分布式维纳滤波器,令星敏感器视场内的某颗导航星(记为S星)方向矢量为,根据星历可得其在惯性系下的投影,利用姿态阵可将其转换到星敏感器坐标系下,得到。记星敏感器焦距为f,光轴(z轴)方向矢量为,则星点质心矢量s为
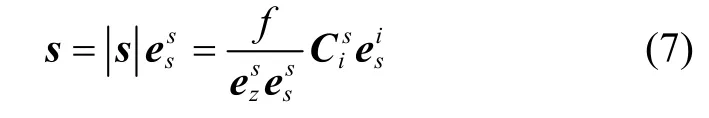

星点与惯性空间固连,故星点质心矢量s在星敏感器坐标系下的旋转角速度亦为,此时星点质心运动速度为


记像平面x轴方向矢量为,则星点运动模糊方向α为
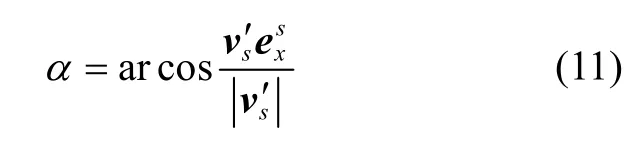
记星敏感器曝光时间为tΔ,单位像素尺寸为ds,则星点运动模糊长度为

至此得到了导航星S所对应的运动模糊参数,但实际一幅星图中存在多颗导航星,当存在绕光轴机动的角速度时,各星点的运动模糊参数都是不同的。最精确的处理方式是先对一幅星图进行遍历扫描,对每颗星点都划分出单独的星点窗口进行维纳滤波。但每一个图像分割窗口都对应一个维纳滤波器,显然当导航星数目较多时,这种方法将导致计算效率的严重降低。临近空间飞行器动态环境较为恶劣,对导航算法的实时性具有一定的要求,在设计图像分割算法时,还应综合考虑计算效率的影响。
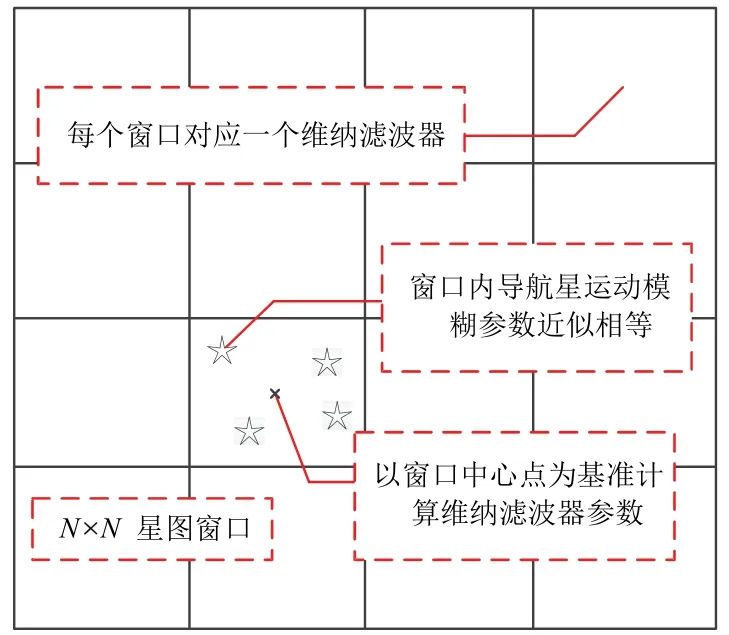
图3 固定窗口分割示意图Fig.3 Fixed window segmentation diagram
本文采用固定窗口分割方法,如图3所示。将一幅星图平均分成N N× 个区间,近似认为每个区间内的导航星运动模糊参数一致。显然N越大算法精度越高但计算量也越大,需要通过计算机仿真获得兼顾精度与计算效率的最优参数N。
2 仿真验证
2.1 天文导航虚拟验证软件平台开发
对于临近空间背景的高超声速飞行器,很难用外场实验的方式模拟临近空间环境下的观测情况,故需要开发虚拟验证软件系统。虚拟软件验证系统的主要目的是:①模拟整个天文导航处理流程,使仿真结果更接近真实情况;②模拟临近空间环境下的星点动态拖尾效应。
按各部分主要功能进行划分,天文导航虚拟验证软件平台主要由以下几个模块组成:
(1)时间模块
该模块的主要功能是:根据当前UTC(世界时)计算儒略日JD、格林尼治恒星时GAST。该模块的输入量为UTC,要实现目标是:①根据GAST计算出瞬时天球坐标系到瞬时地球固连坐标系的转换矩阵;②为后续其他修正模块提供时间基准JD。
(2)导航星库修正模块
该模块的主要功能是:根据时间基准JD和导航星表参数修正恒星自行、完成星表划分、剔除双星三种功能。
为提高对全天星表的检索效率,需要对导航星表进行分割,通常星表分割采用赤纬带、球矩形等方法。但这些方法存在导航星数目分割不均匀的问题,即越靠近两极,导航星数目越少。为解决上述问题,本文提出一种基于C60 分子结构的全天星表分割方法,这样可将全天分成32 个天区,每个天区为正五、六边型,还可进一步将每个天区分成5、6 个小天区,小天区为正三角形。星表分割如图4所示。

图4 全天星表分割示意图Fig.4 Schematic diagram of all sky catalogue segmentation
(3)地球参数修正模块
该模块的主要功能是:根据时间基准JD计算地球岁差、章动、极移和光行差修正矩阵。其中地球岁差、章动采用IAU1980 模型;极移数据来自国际地球自转服务(International Earth Rotation Service,IERS);光行差修正涉及的地球参数来自DE405 模型。
(4)星图模拟模块
该模块的主要功能是:根据星敏感器位置、姿态、时间、视场进行视场内的导航星图模拟。
(5)星图预处理模块
该模块的主要功能是:星图背景过滤、导航星窗口提取和星点质心提取。
(6)天文导航解算模块
该模块的主要功能是:采用三角形算法进行星图识别,然后根据星图识别结果进行姿态解算,输出星敏感器姿态解算结果。
天文导航虚拟验证软件平台框图如图5所示。
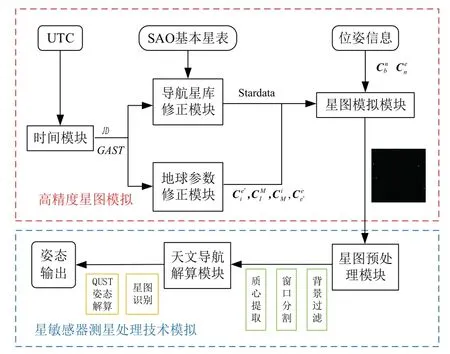
图5 天文导航虚拟验证软件平台原理框图Fig.5 Schematic diagram of celestial navigation virtual verification software platform
2.2 临近空间飞行器标称轨迹仿真
以临近空间飞行器为仿真对象,仿真中采用的飞行器气动参数来自文献[14]。设飞行器初速度为5 Ma,初始纬度、经度为40 °、120 °,高度30 km,航向正东、俯仰30 °、滚转0 °,假设飞行过程中机头指向始终与速度方向一致(姿态约束),其余模型参数如表1。仿真轨迹如图6所示。

表1 仿真器件参数Tab.1 Simulated device parameters
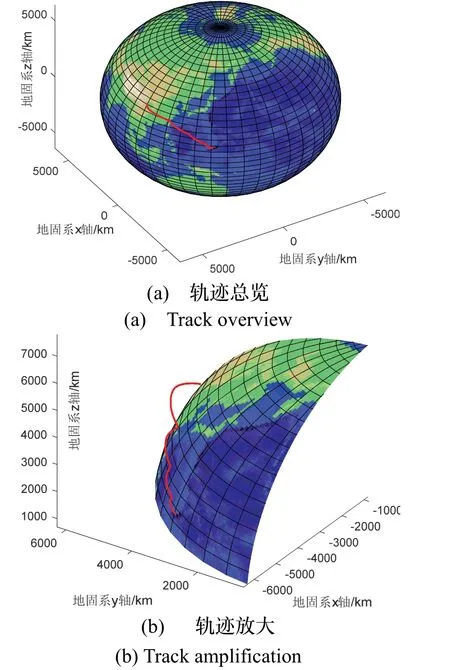
图6 三维仿真轨迹Fig.6 Three-dimensional simulation trajectory
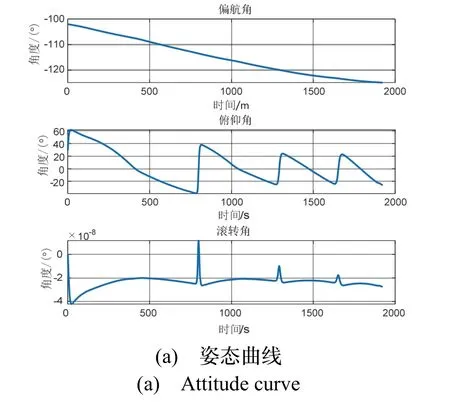
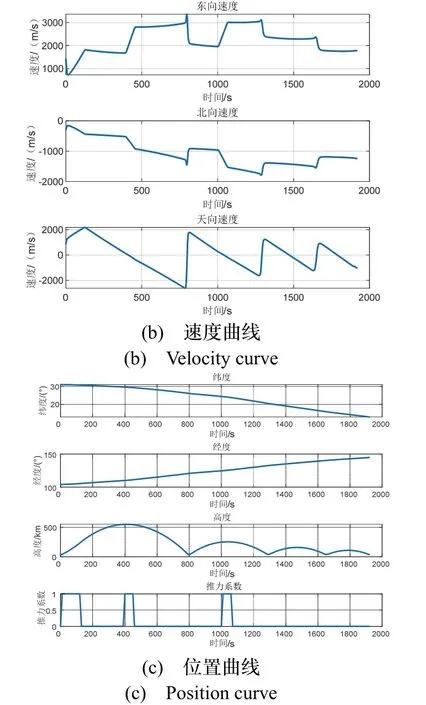
图7 轨迹仿真曲线Fig.7 Trajectory simulation curve
从轨迹姿态和角速度仿真曲线(图7所示)可以看出,临近空间飞行器在再入大气层时,由于气动力的作用会导致飞行器俯仰轴出现大姿态机动,角速度在4 °/s 左右。对于天文导航系统,由于图像曝光需要一定的积分时间,因此在大姿态机动时极易产生星图拖尾现象。
2.3 集中式与分布式维纳滤波效果对比
设置载体绕光轴以30 °/s 的角速度进行姿态机动,星敏感器曝光时间设为0.1 s,得到星敏感器视场内观测到的拖尾图像如图8所示。

图8 拖尾星图模拟结果Fig.8 Simulation of trailing star map
图8(a)展示了绕光轴机动时视场内不同导航星拖尾参数的差异性,不同位置的星点模糊长度xyL和模糊方向α均不一致,显然此时采用集中式维纳滤波无法对整幅星图进行复原。图8(b)增加了背景噪声,从这里可以看出星图拖尾效应的另一个负面影响,即星图拖尾会导致星点能量分布不集中,此时拖尾效应严重的星点亮度急剧下降,几乎淹没在背景噪声中,这对后续的星点提取是十分不利的。
然后对比集中式维纳滤波和分布式维纳滤波的图像复原效果。设置载体自由机动,绕星敏感器三轴角速度分别为2 °/s、2 °/s、10 °/s(光轴方向拖尾效应不明显故提高一个量级)。对比集中式维纳滤波和分布式维纳滤波的图像复原效果,仿真结果如图9所示。

图9 拖尾星图复原效果对比Fig.9 Restoration effects comparison of trailing star images
在图9(b)中用白色框线标注了复原星图中的四种典型星点形状,显然位于图像中心矩形框内的星点复原效果较好,而边缘圆形框内的星点没有得到有效的复原,星点拖尾依然存在。综合来看,在进行拖尾星图复原时,复原后的星点有如图10所示的四种典型特征。

图10 复原星图中四种典型星点Fig.10 Four typical restored star points in star map
其中,Ⅰ型星点为正确复原的星点,从图10(a)、(b)中可以看出星点得到了较好的复原;Ⅱ型星点复原后能量反而分散了,这是因为在进行维纳滤波时,图像的运动模糊参数xyL取值偏大,导致星图复原过量;Ⅲ型星点与Ⅱ型星点恰好相反,复原后星点能量分布稍微集中一些,但依然存在拖尾现象,显然是在进行维纳滤波时xyL取值偏小,导致星图复原不充分;Ⅳ型星点复原后拖尾效应并没有改善,而且拖尾方向发生了变化,这是因为在进行维纳滤波时图像的运动模糊方向α不匹配,导致复原时角度出现错误。
图9(b)展示的是4×4 分布式维纳滤波结果,可以看出此时由于采用了分布式滤波,各部分的星点均得到了较为完善的复原。在进行窗口分割时,4×4 的分割方式已能满足精度需求,2×2、8×8 分割方式下的维纳滤波复原星图如图11所示。


图11 拖尾星图复原效果对比Fig.11 Restoration effects comparison of trailing star images
如图11所示,2×2 分布式维纳滤波复原后星点依旧存在较为明显的拖尾,而8×8 分布式维纳滤波复原效果与4×4 分布式维纳滤波相比并没有显著的提高,考虑到算法计算效率,应选择4×4 分布式维纳滤波构建临近空间高超声速飞行器的星图复原算法。
2.4 拖尾星图复原前后质心提取精度对比
拖尾图像复原精度直接影响星点质心提取精度,间接影响最终导航精度,本文进行1000 次蒙特卡洛打靶仿真,统计图像复原前后的星点质心提取精度和最终姿态解算精度,仿真中采用的质心提取方法为平方加权质心法,姿态解算方法为QUEST 算法,质心提取精度统计结果如图12所示。

图12 拖尾图像复原前后质心提取精度统计Fig.12 Statistics of centroid extraction for star image restoration
如图12所示,本文采用的拖尾图像复原算法,可将星点质心提取精度由原来的0.059 像素提高到0.046,质心提取精度提高了20%。接下来统计姿态精度,结果如图13所示。

图13 拖尾图像复原前后姿态解算精度统计Fig.13 Statistics of attitude resolution for star image restoration
拖尾图像复原后,可将姿态解算精度由原来的25.9 ″(3σ)提高到23.7 ″(3σ),姿态精度提高了10%,在1000 次打靶中,拖尾星图处理前星点提取、匹配失败139 次,准确率为86.1%,复原后星点提取、匹配失败78 次,准确率92.2%。
2.5 拖尾星图复原前后导航精度对比
对第500 s~520 s 轨迹数据进行仿真,对比图像复原算法前后天文导航姿态解算结果如图14所示。
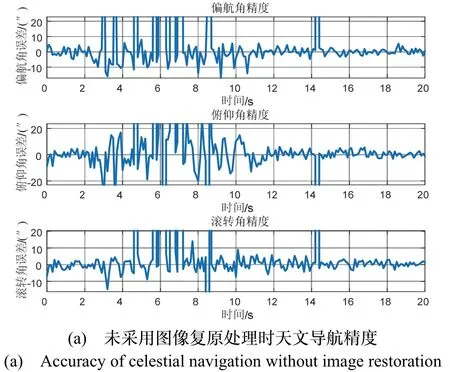
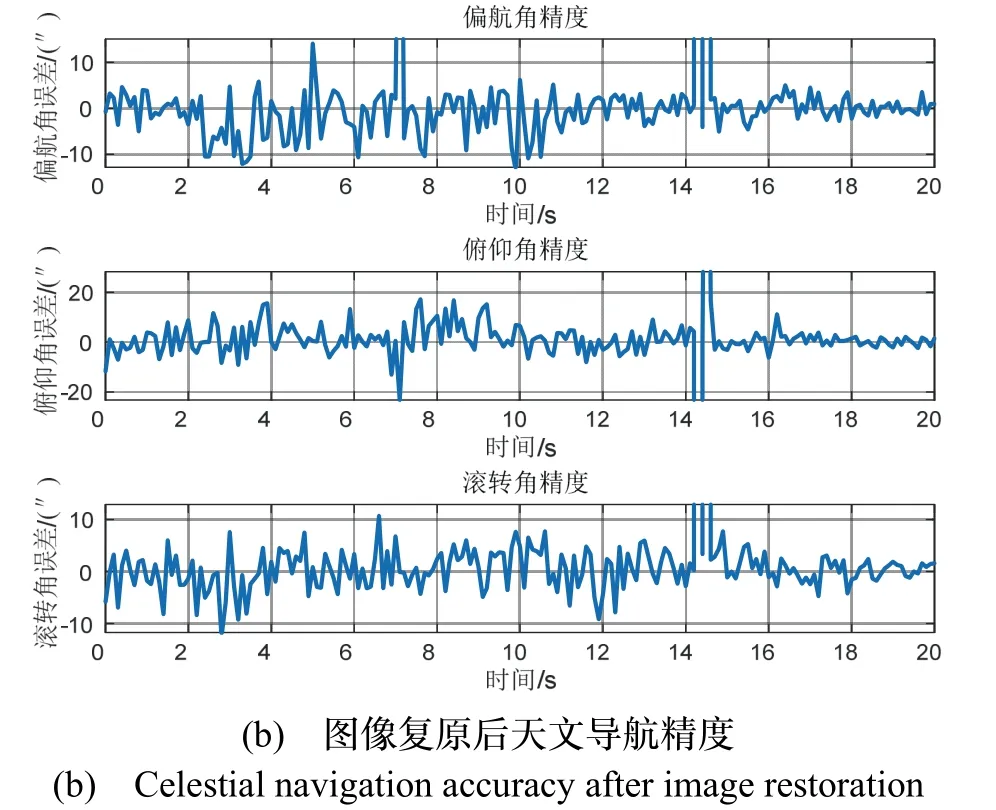
图14 星图复原前后天文导航精度对比Fig.14 Comparison of celestial navigation accuracy after star map restoration
图14(a)中的曲线跳变是星点匹配错误导致的,在仿真开始后的4 s~12 s 内,角速度达到峰值,此时曲线出现剧烈跳变,若不采用图像复原算法,天文导航基本处于不可用状态;图14(b)中曲线跳变明显减少,仅有的几次跳变可以作为量测野值处理,图像复原后天文导航算法可以正常工作,姿态精度可维持在20 ″(3σ)以内。
4 结论
首先,本文为提高算法的计算效率引入IMU 测量信息计算星点运动模糊参数。然后,针对传统维纳滤波无法对光轴方向的拖尾进行复原的缺陷,提出了一种图像分割分布式维纳滤波复原算法。最后基于临近空间飞行器飞行特性设计了虚拟软件验证平台,针对标称轨迹模拟了临近空间飞行器动态拖尾星图并进行虚拟仿真验证。仿真结果表明,图像分割分布式拖尾星图复原方法可对拖尾星图进行有效复原,复原后姿态精度优于20 ″(3σ),质心提取精度提高了20%,姿态精度提高了10%,星点提取、匹配成功率增加6%。本文所提出的方法能对动态环境下的拖尾图像进行有效复原,算法简洁,工程可行性高,可为未来临近空间飞行器天文导航算法的设计提供一定的理论参考。

