基于AR建模的组合导航系统渐变故障双阈值检测方法
吕 旭,胡柏青,戴永彬,高端阳
(1.海军工程大学 电气工程学院,武汉430033;2.辽宁工业大学 电气工程学院,锦州121001)
捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)具有较好的自主性和隐蔽性,能够连续提供多种导航参数,频带宽,抗干扰好,但其误差随时间不断累积[1,2]。相反,全球卫星导航系统(Global Navigation Satellite System,GNSS)的测速和定位精度高,且基本不受地域、时间限制,但导航的精度和可靠性与载体的运动和信号的通透性有关,且抗干扰能力差,信息的更新率低[3]。基于两者优势互补,目前,使SINS/GNSS 组合导航的应用越来越广泛[4]。SINS具有较高的可靠性,故障率较低。一旦GNSS 系统发生故障,经滤波信息融合后,将导致组合导航系统整体受污染,输出信息精度降低,可靠性得不到保障,甚至难以定位。因此,及时有效地检测组合导航系统的信息故障,提高组合导航系统的可靠性,开发故障检测和隔离方法是非常必要的。
容错设计的出发点就是从系统的整体设计来提高其可靠性,通过系统检测发现故障。目前,在已有的组合导航系统级故障检测方法中,状态χ2和残差χ2检验法最为常用[5,6]。这两种方法分别通过构造状态或残差信息统计量,根据服从的概率统计分布来判断组合导航系统中是否出现故障,具有不需要确定故障的具体原因的特点[7]。但是这两种方法也存在一些不足,其中状态χ2检验法,由于状态更新导致系统误差累积,故障检测灵敏度降低,而且计算相对复杂[8]。与状态χ2检验法比较,残差χ2检测法算法简单,实时性更好。但是该方法通常对突变故障有效检测,针对渐变故障检测效果不佳,甚至失效[9]。因此,故障检测灵敏度和准确率在组合导航实际应用过程中都得不到保障。
针对上述问题,诸多学者进行了相关理论探讨与研究。文献[10]采用残差χ2检测方法构造新息调节因子,自适应修正量测噪声协方差矩阵,但是该方法对渐变故障检测的效果较差,在一定程度上算法性能受限。文献[11]采用双状态χ2检测方法,虽然该方法通过切换状态递推器避免了渐变故障“跟踪”的问题,但是该方法对故障的检测缺少一定的准确性,针对小幅值故障并未进行有效检测,且状态递推反复切换也会增加系统误差的产生。文献[12]通过状态χ2检验法和残差χ2检验法相互配合,提高系统信息故障检测的准确性,但难以兼顾实时性,并且渐变故障的检测效果不佳。近几年,随着机器学习的发展,神经网络[13]和支持向量机[14,15]等故障检测方法也相应提出,但是以上方法均需要大量的数据训练搭建模型,或是构建新的统计量,计算量大且很难兼顾好实时性。因此,为了解决组合导航系统中渐变故障检测以及检测灵敏度降低问题,研究一种新的故障检测方法及控制策略具有重要理论意义和实践价值。
综上,本文结合系统的物理特性,从实际角度出发,提出了一种基于AR建模的组合导航系统渐变故障双阈值检测方法。通过建立无故障条件下静态或运动观测数据的AR 模型,结合卡尔曼滤波框架得到量测预报值进行残差计算,自适应调节滤波增益矩阵,降低检测统计量“跟踪”故障问题;在此基础上搭建双阈值检测门限,针对小幅值故障,采用该双阈值门限进行分类处理,降低了漏警率对数据可靠性的影响。本文所提出方法应用到SINS/GNSS 组合导航系统中,通过仿真实验分析,验证该方法对渐变故障检测的有效性。
1 残差 χ 2检验法性能分析
残差χ2检验法中,残差即是系统实际量测值与量测估计值的差,通过构造残差检测函数判断是否服从已知期望和方差高斯分布,对系统故障进行实时有效检测。考虑常用带故障的离散系统动态模型:
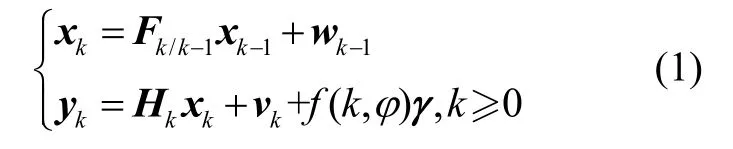
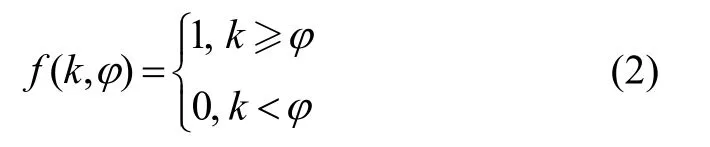
式中,φ为故障发生的时间。
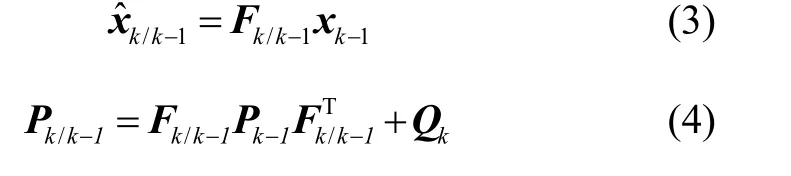
量测预测值为:

量测残差向量可表示为:

式中,rk表示残差,即量测值与量测预测值的差值,通常也称为“新息”。
可以证明,在无故障时,根据卡尔曼滤波假设推导可知,残差rk是服从零均值高斯白噪声分布,其方差为:
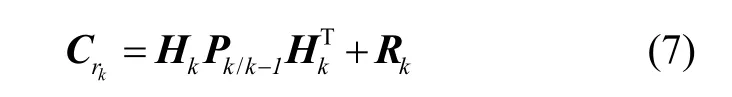

由新息统计特性可知,λk~χ2(m)服从自由度m的χ2分布,其中m为量测yk的维数。判定系统是否发生故障的二元假定依据为:1)H0:λk≥TD认定系统发生故障;2)H1:λk﹤TD认定系统正常工作。TD为预设检测门限,该门限与误警率相关,设α为误警率,存在;设β为漏警率,则有,且满足式(9)[16]。
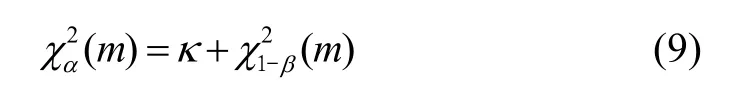
式中,κ为检验函数的非中心化参数,定义如下:

此时阈值与漏警率确定的最小可检测误差为:
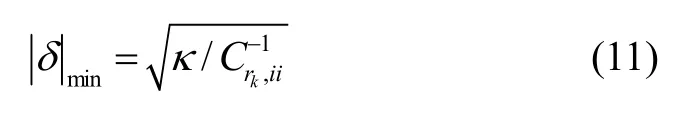
误警率与漏警率[17]的关系如图1所示。
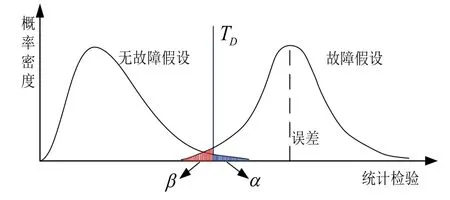
图1 误检率与漏检率之间的关系Fig.1 Relationship between probability of false alert and missed detection
残差χ2检验,判定系统信息故障与否的关键是由残差所得检测函数值是否超过预先设置的门限。残差χ2检验对于突变故障检测十分有效。针对渐变故障问题,显然有很多不足。由图1 可知,检测阈值TD的选择需要在误警率与漏警率之间折中。而且,漏警率的大小与最小检测误差具有直接关系。当故障值大于最小检测误差时,故障越容易被检测,漏警率小;反之,检测不到系统故障信息,导致误警率大。
2 AR 量测建模辅助的故障检测方法
该方法通过时间序列分析中AR 方法对组合导航系统中的量测信息建立自回归模型,得到非“跟踪”信息故障输出的系统量测预报值,构造双阈值检测门限提高数据质量,进而提高了残差χ2检验法对组合导航系统渐变故障的检测灵敏度及准确性。
2.1 AR 量测建模
自回归模型(Autoregressive Model,简称AR 模型)是一种时间序列分析方法,利用组合导航系统量测历史数据,通过建立无故障条件下量测预报值的AR模型,可以得到基于AR建模的量测预报与样本空间的前若干时刻量测均相关,当渐变故障发生时,受到故障的影响较小,不会“跟踪”故障输出,所得残差rk值较大,因而对于渐变故障能够进行有效地检测。以SINS/GNSS 组合导航系统速度量测为例,连续采集系统在静止和运动时的速度量测数据,证明无论是静态还是动态情况,速度量测的序列均具有明显的自相关性。根据SINS/GNSS 组合导航系统速度量测特性,采用AR 模型来描述和预测SINS/GNSS组合导航系统速度量测的变化规律。
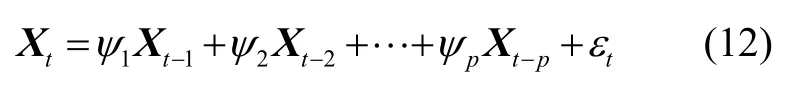
式中,ψ1,ψ2…ψp为自回归系数,P为AR 模型的阶数,εt为零均值高斯白噪声。
将向量Xt转化为标量后,可得AR(p)模型[18]。
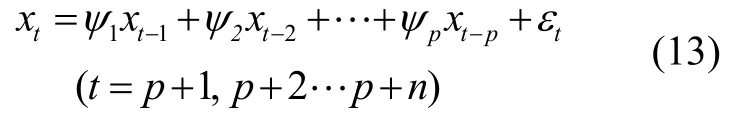
式中,自回归系数ψ1,ψ2…ψp由序列自协方差函数γ1,γ2…γp通过Yule-Walker 方程(14)唯一确定。
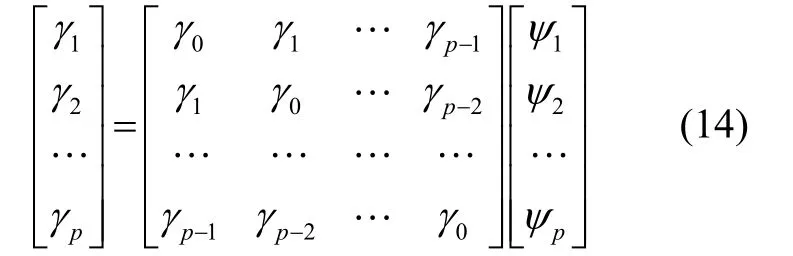
式中,εt高斯白噪声方差σ2为:
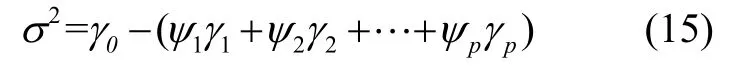
采用上述方法估计出AR 模型的参数,得到各阶次的模型。但是,需要事先确定模型的阶数,通过一些准则来比较并选出最适合的模型。模型阶次选择,通过Akaike 信息准则选取,简称为AIC 准则[19]。当用AR(p)进行量测建模时,可得,其与阶次p的函数关系如式(16)。
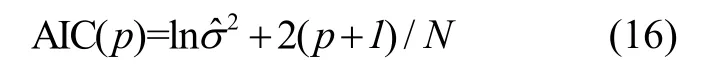
式中,p+1为待估计参数个数,包括自回归系数ψ1,ψ2…ψp和随机误差的方差σ2。N为序列个数。当第二项中阶次p增加时,模型的极大似然函数单调下降,当模型阶数增加至p0值时,AIC(p0)达到极小,此时p0为模型最优阶次。
2.2 基于AR 量测建模的双阈值故障检测法
残差χ2检测法因其对突变故障检测效果良好被广泛应用,但是残差χ2检测法对渐变故障的检测不是十分有效,如对故障敏感度低、检测效果差、容易漏检等。这是由于渐变故障开始很小,不易被检测,有故障输出将会影响状态一步预测,使它“跟踪”故障输出,导致残差持续较小,因此很难应用传统方法发现故障。针对这一问题,在结合AR 建模优势基础上,采用双阈值故障检测,提高系统的可靠性。
传统残差χ2检测法单一门限的设定,很难在误警率与漏警率之间进行折中,二者不可兼顾。所以,本文采用双阈值方法,设定大小阈值对故障是否发生进行检测。判定系统是否发生故障的假定依据为:1)认定系统发生故障;2)认定系统正常工作;3)认定系统被干扰。TD1和TD2为预设检测大小门限,误警率为α1和α2。通过以上分布式处理,提高系统对小幅值渐变故障的检测质量。
采用AR 量测建模的双阈值故障检测系统,具体检测流程如下:
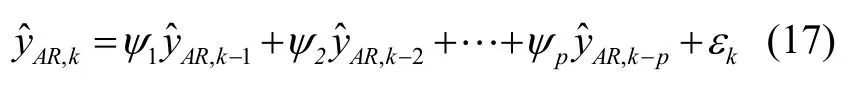
步骤2:结合式(5)(6)得到基于AR量测建模的k时刻残差:

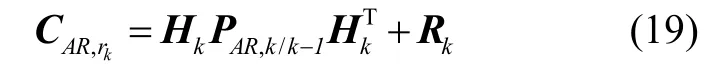
步骤4:求得系统故障检测函数为:
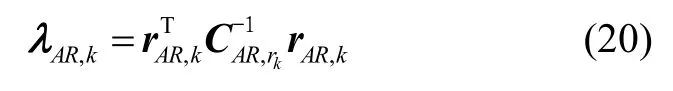
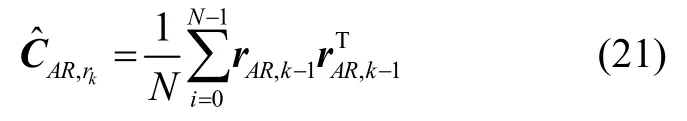
式中,N为残差序列窗口长度,通过可求得新的卡尔曼滤波增益矩阵为:
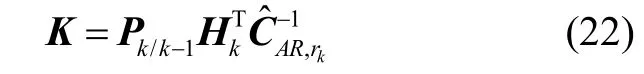
式(22)对滤波增益起到了自适应调节的作用,由于AR 量测建模的预报值受故障“跟踪”影响较小,以至于求取的新息协方差矩阵较大,因为与滤波增益负相关,在一定程度上提高了系统对小幅值故障的敏感性和算法精度。
3 仿真实验验证
3.1 SINS/GNSS 组合导航系统模型
本文通过SINS 和GNSS 对载体运动进行参数测量,建立SINS/GNSS 直接式松组合导航模型。系统状态方程采用惯导基本方程,量测方程采用GNSS 输出的速度信息作为辅助校正。通过UKF 方法进行信息融合,定义载体系为b 系,惯性系为i 系,导航系为n系,地理系为e 系。SINS 基本微分方程具体如下[20]。

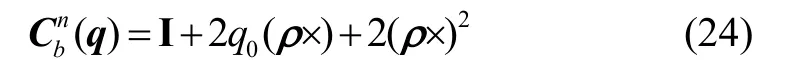
比力方程和位置微分方程具体如下:
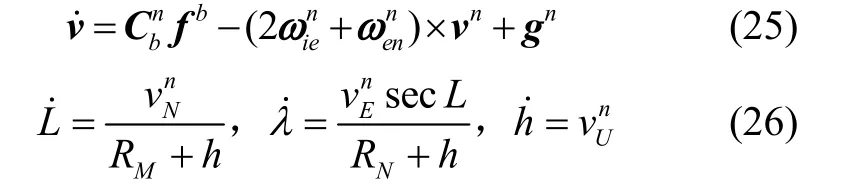
量测模型采用速度量测,量测方程为:

3.2 仿真实验分析
为了验证所提的AR 建模双阈值故障检测法的有效性,与传统残差χ2检测法以及双阈值残差χ2检测法进行对比。仿真实验模拟车辆运动,仿真时间为500 s。初始位置为北纬34.246 °,东经108.909 °,记录其运动参数。其中GNSS 位置误差为10 m,输出频率1 Hz,SINS 更新频率为10 Hz。由于在SINS/GNSS组合导航中使用了速度松组合的配置,滤波器在没有GNSS 信息输出时执行状态更新。初始航向误差为1 °;陀螺仪常值漂移为0.1 °/h,随机游走系数为0.01 °/h;加速度计零偏为100μg,随机游走系数为。如图2所示的运动轨迹。
为模拟真实使用环境,现假设SINS 系统可靠,GNSS 系统发生故障,设置故障条件主要包含三种情况。情况1:无故障情况对比;情况2:GNSS 东向速度在200 s-280 s 加入突变故障离群值;情况3:GNSS东向速度测量在200 s-280 s 加入(0.6 ×(t-200))/10的渐变故障。AR 量测预报的时间序列建模点迹数目为200 个,故障告警的条件设置为检测统计函数连续5 s超过阈值,而连续5 s 低于检测阈值视为故障结束。设置故障检测的误警率为α1=0.6和α2=0.2,则有门限TD1=6.21和TD2=3.83。为了验证本文所提方法的有效性,分别在情况1 无故障条件、情况2 突变故障条件和情况3 渐变故障条件下,对比传统残差χ2故障检测方法(M1)、改进的双阈值残差χ2故障检测方法(M2)以及本文所提出的基于AR建模的双阈值残差χ2故障检测方法(M3)三种检测方法的检测性能。M1 方法:当传统卡方检测到报警时,为了提升系统的容错能力,期间故障隔离,采用只进行惯导状态更新,直至故障检测结束重新加入量测更新。M2 方法:改进的双阈值残差χ2故障检测方法,当检测量位于双阈值之间时,进行自适应调节滤波增益方法进行容错;当故障检测量超过门限TD1时,处理方法同情况1。M3 方法:情况3 处理方法同情况2 处理方法。
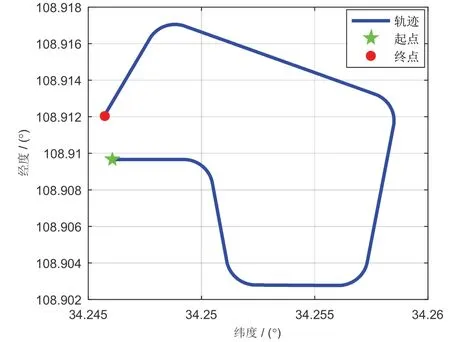
图2 仿真轨迹Fig.2 The simulation trajectory
在对AR 模型进行识别时,根据其样本偏自相关的系数的截尾步数,可得AR 模型阶数p,根据AIC 准则使AIC(p0)达到极小,AIC 值随阶数变化情况如图3所示。
从图3 可知,当阶数p<4 时,AIC 值变化幅度较大;当p>6 时,AIC 值随着阶数的增加而缓变减少;当阶数达到10 时候,AIC 值基本不变,但是相应计算量也会增加。因此,选择适合的阶数是提高AR 模型性能的前提依据,最终确定阶次不宜过高为6 阶。得到AR 量测建模的参数为:ψ1=1.1775,ψ2=0.2669,ψ3=-0.2136,ψ4=-0.1905,ψ5=-0.0408,ψ6=-0.0033。
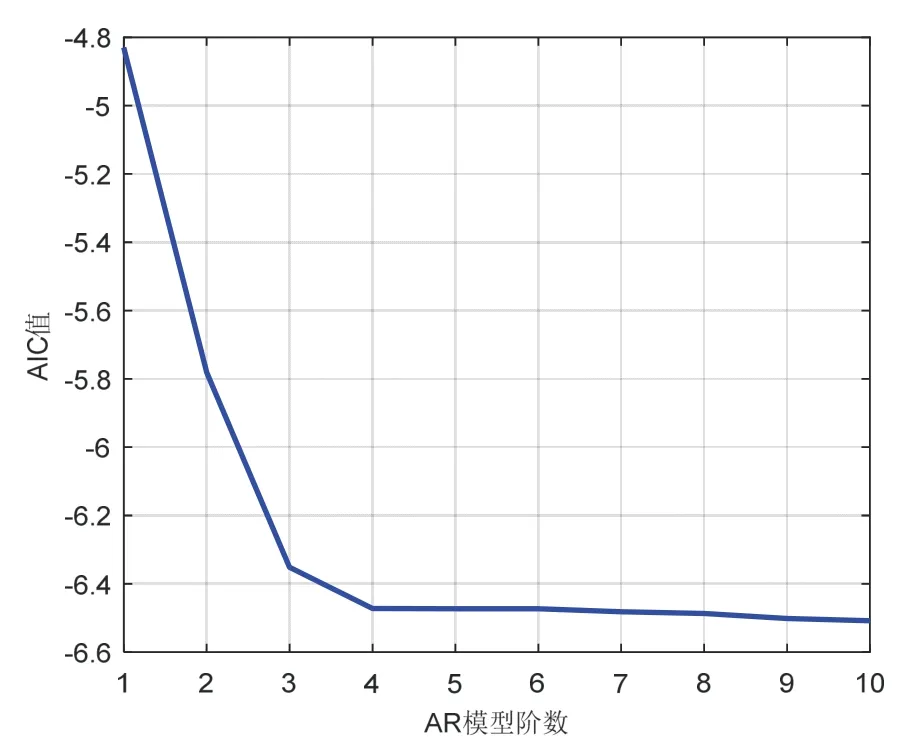
图3 AIC 值随阶数变化图Fig.3 Variation of AIC value with order number
情况1 系统无故障发生条件下,比较本文所提及三种故障检测法性能,如图4-6所示。
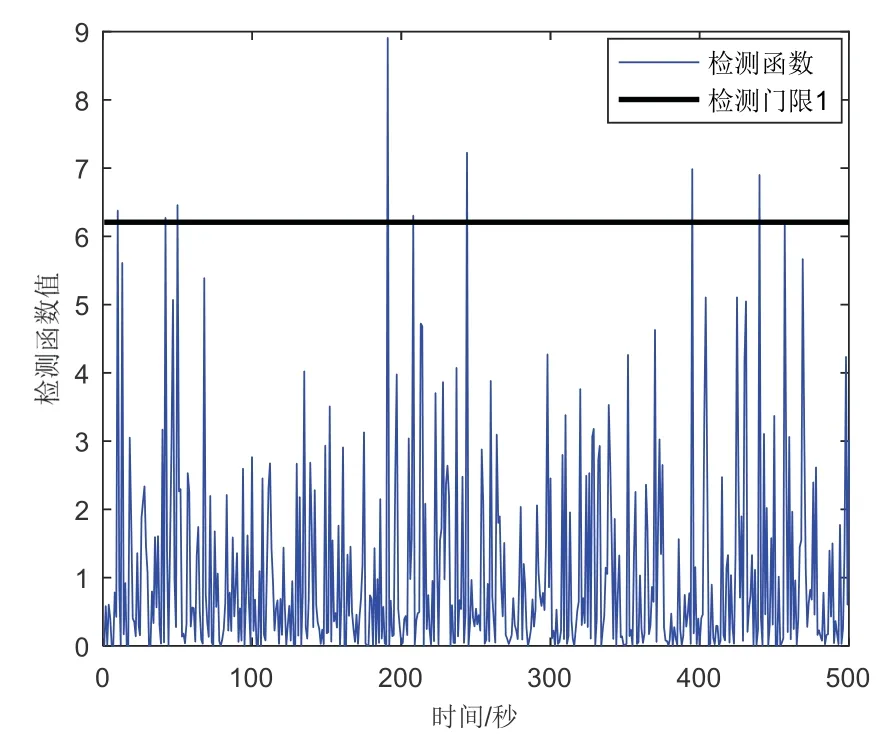
图4 情况1 下残差χ 2检验Fig.4 The residualχ 2test under case 1
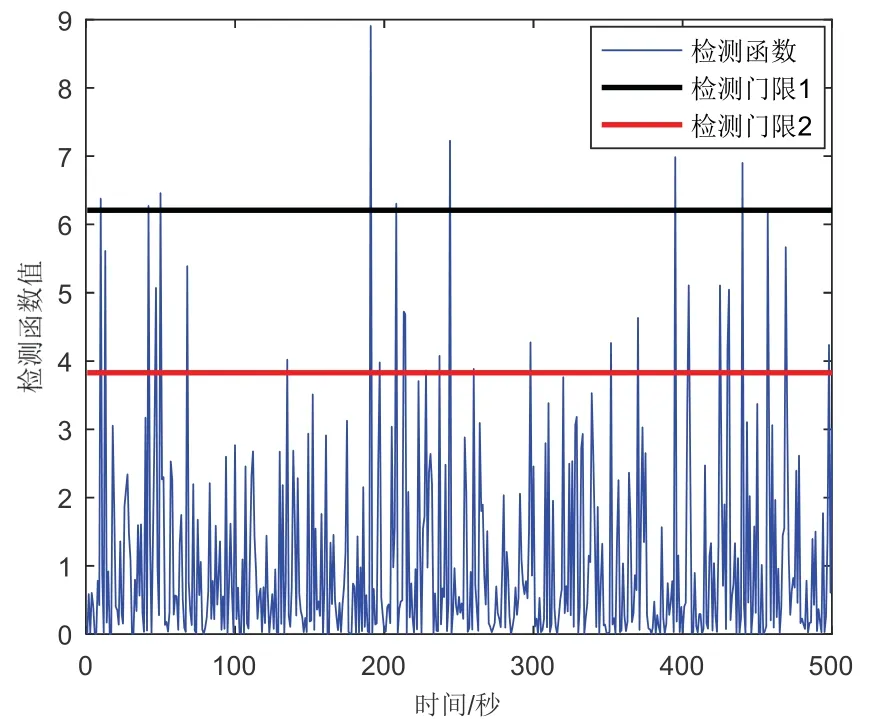
图5 情况1 双阈值残差χ 2检验Fig.5 The double threshold residualχ 2test under case 1
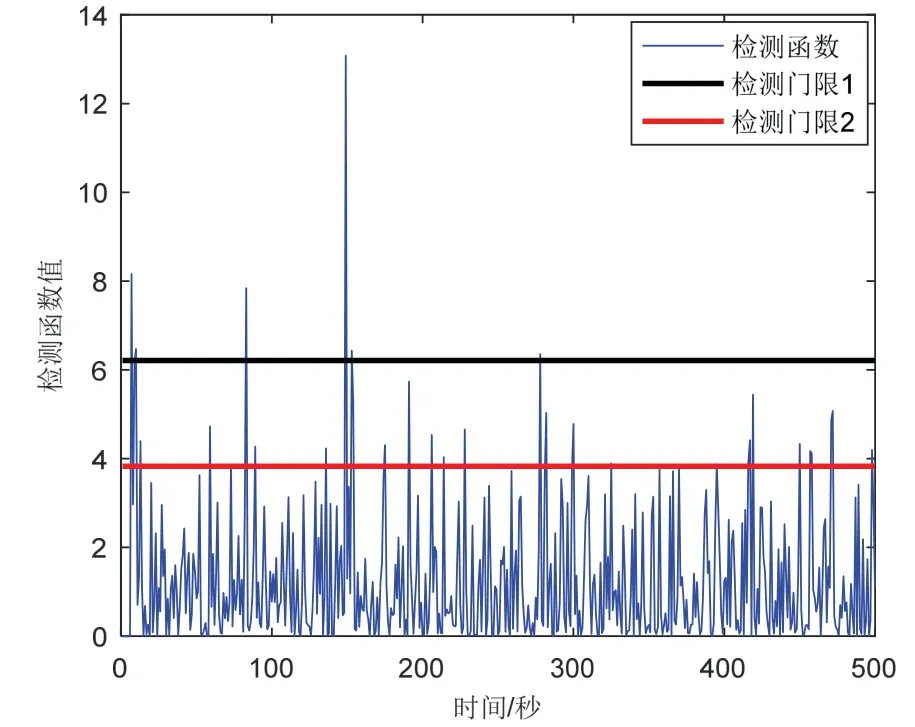
图6 情况1 AR 建模的残差χ 2检验Fig.6 The residualsχ 2test for AR modeling under case 1
由图4-6 可知,三种故障检测方法在无故障条件下,均未触发报警功能,检测效果相当。但是,相比于传统的残差χ2故障检测方法以及改进后的双阈值残差χ2检测方法,本文提出的AR 建模的组合导航系统渐变故障双阈值检测方法,检测统计量相对均衡稳定,且幅值较小,说明本文所提出的方法得到的量测建模数据更为准确。
情况2,当系统突变故障发生时,比较本文所提及三种故障检测法性能如图7-9所示。可知,当系统在200 s-280 s 时间段内发生突变故障时,本文提及的三种故障检测方法对突变故障的检测灵敏度均较高,但是传统残差χ2检测法由于量测污染“跟踪”故障,在212 s 和268 s 之间出现漏检现象。改进的残差双阈值χ2检测方法出现漏检现象时能进行自适应调整,缓解漏检问题。
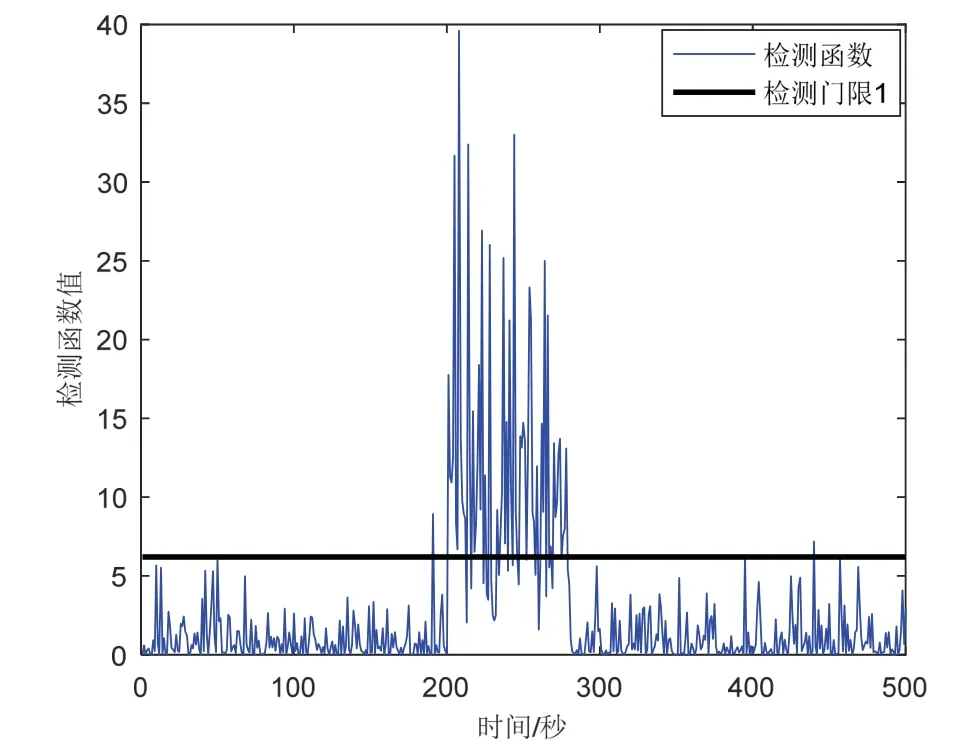
图7 情况2 残差χ 2检验Fig.7 The residualχ 2test under case 2
本文所提出的故障检测方法,有效避免了量测“跟踪”故障问题,对于组合导航系统突变故障有效检测的准确性能有所改进。特别是,由于三种算法针对突变故障检测灵敏度一致,双阈值自适应调节策略对于突变故障的处理效果不显著。但是,当故障检测统计量大于检测阈值时,将进行故障隔离,组合导航只进行状态更新,直至检测到故障结束后再进行量测更新。相应三种方法的容错效果基本一致。
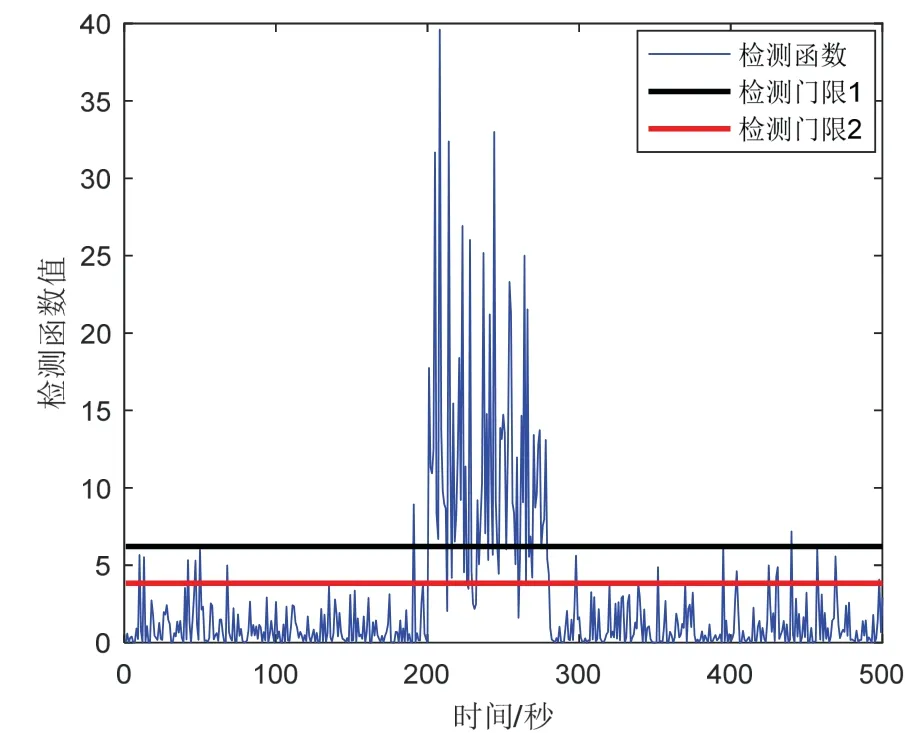
图8 情况2 双阈值残差χ 2检验Fig.8 The double threshold residualχ 2test under case 2
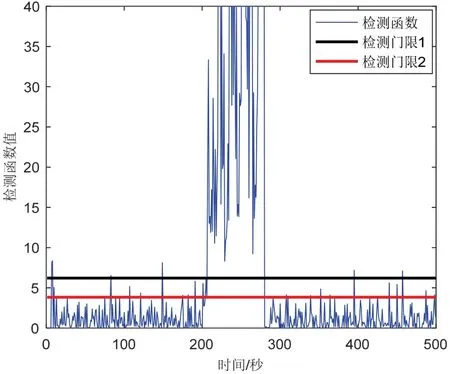
图9 情况2 AR 建模的残差χ 2检验Fig.9 The residualsχ 2test for AR modeling under case 2
情况3,当系统渐变故障发生时,比较本文所提及三种故障检测法性能如图10-12所示。
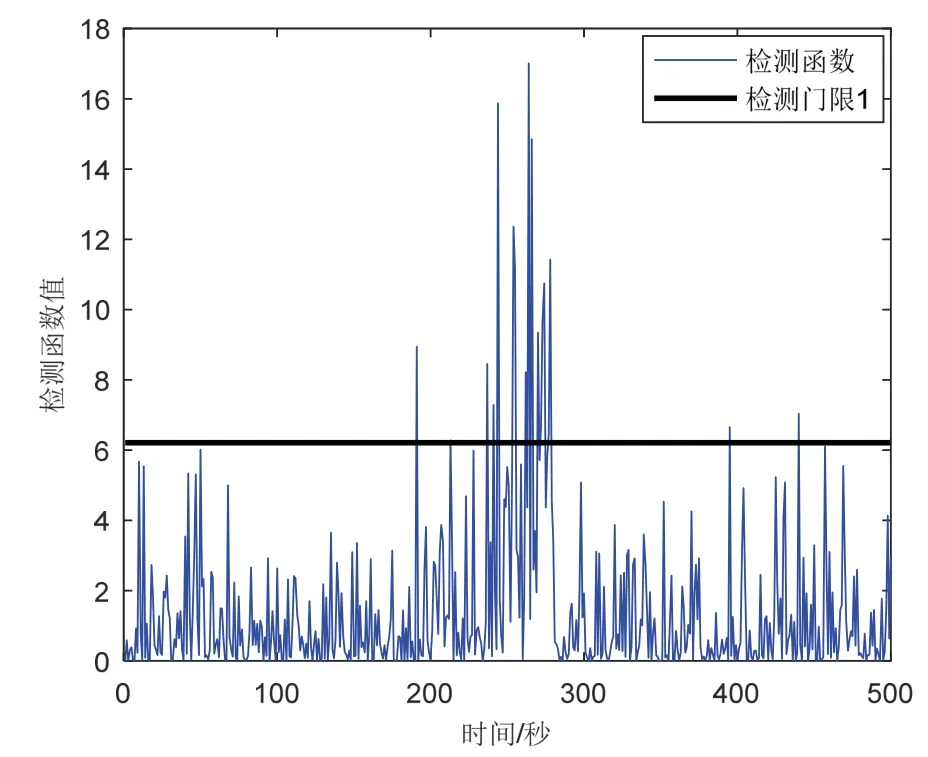
图10 情况3 残差χ 2检验Fig.10 The residualχ 2test under case 3
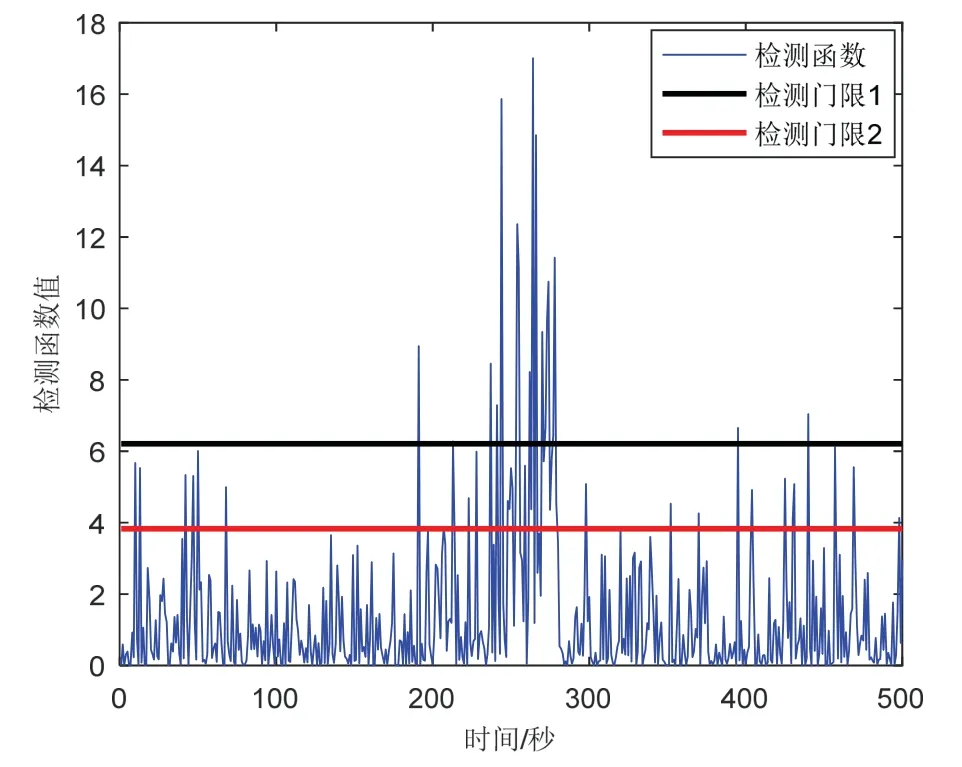
图11 情况3 双阈值残差χ 2检验Fig.11 The double threshold residualχ 2test under case 3
从图10-11 可知,传统的残差χ2检测法和改进的双阈值残差χ2检测法,由于渐变故障“跟踪”原因,导致最终的检测统计量效果并不明显。残差数据因受到量测信息引入故障,通过卡尔曼滤波框架导致“跟踪”故障变化较小,始终无法达到告警条件,因而无法及时检测出系统渐变故障,出现了漏检的现象。
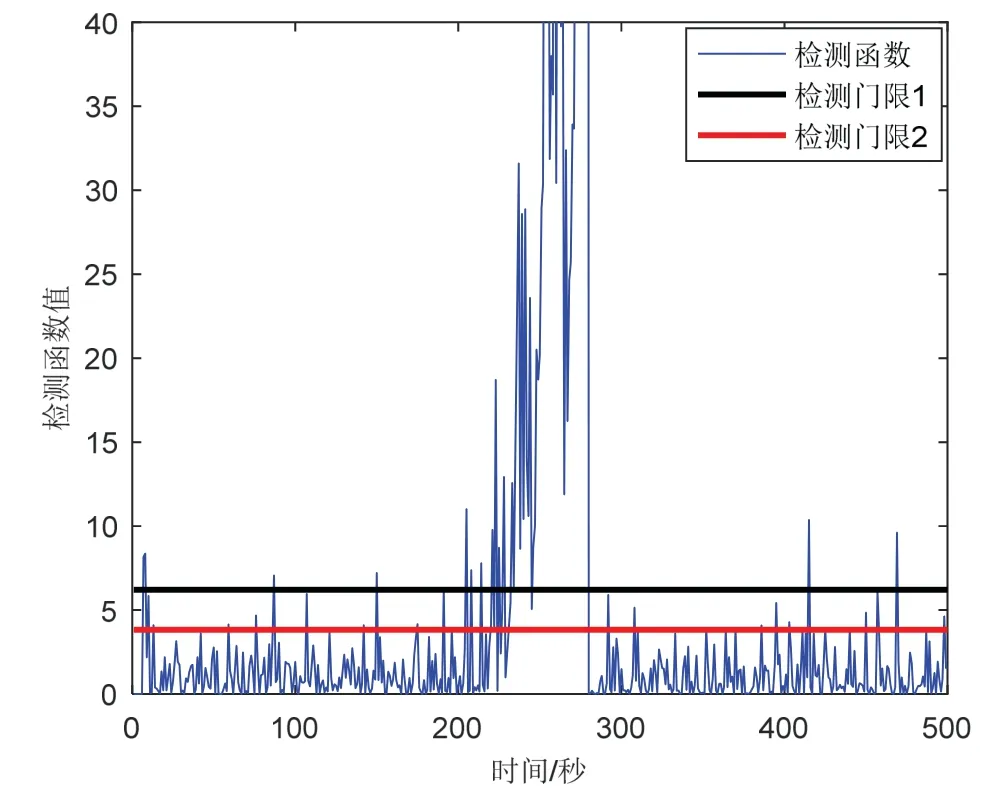
图12 情况3 AR 建模的残差χ 2检验Fig.12 The residualsχ 2test for AR modeling under case 3
由图12 可知,对于小幅值渐变故障,相比于传统方法,本文方法采用AR 量测建模策略,有效避免了“跟踪”故障对系统检测的影响,具有更好的检测效率。
为进一步说明本文所提方法的有效性,分析三种故障检测方法,对组合导航系统发生渐变故障时的整体稳定性的影响。以东向速度误差为例进行分析。图13 为未进行故障检测及隔离、传统方法隔离、改进的传统方法及本文所提方法的组合导航系统东向速度误差曲线。
从图13 中可以看出,在系统渐变故障发生期间,传统故障检测方法在未进行故障隔离的情况下,系统在260 s 时东向速度误差达到最大值0.6 m/s 左右。经故障隔离后的传统的方法容错性能较差。基于双阈值的改进残差χ2检测法,在一定程度上将误警率与漏警率之间的检测信息进行了自适应容错处理,系统故障检测性能有所提高。但是,由于以上方法均通过卡尔曼滤波框架,导致系统“跟踪”故障,最终检测效果不明显。相比而言,本文所提出的基于AR建模的组合导航系统渐变故障双阈值检测法,通过建立无故障条件下观测数据的AR 模型,结合卡尔曼滤波模型得到量测预报值进行残差计算,减少了系统“跟踪”故障的发生;在此基础上搭建双阈值检测门限,对误警率与漏警率之间的受污染的观测数据,采用该双阈值门限进行分类处理,自适应调节滤波增益矩阵,降低了漏警率对数据可靠性的影响。图中四条曲线所对应的东向速度均方误差MSE 为0.0901 m/s、0.0877 m/s、0.0822 m/s 和0.0666 m/s,显然本文所提方法东向速度误差受“跟踪”故障影响较小,验证了该方法的有效性。
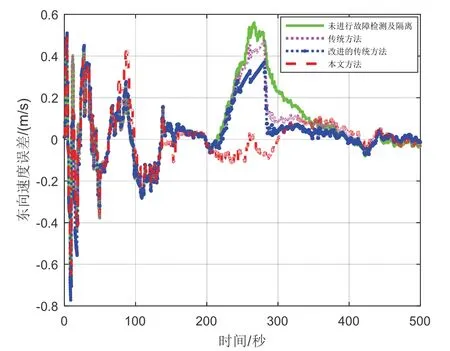
图13 东向速度误差对比Fig.13 The comparison of east velocity
表1 列出了本文所提及的三种故障检测方法的检测性能对比。我们从表中可知,本文提出的基于AR建模的双阈值组合导航渐变故障检测方法,对比传统的残差χ2故障检测法和改进的残差χ2检测法,检测漏警率降低69%以上,整体滤波精度可提高19%以上,能够以较高的灵敏度及时检测到渐变故障并进行容错和隔离。证明了该方法在检测渐变故障时的优越性。
为了进一步充分验证本文所提方法的有效性,继续减小渐变故障的幅值,当故障大小为(0.6 ×(t-200))/20时,基于AR 建模双阈值故障检测法的检验效果如图14所示。从图14 中可以看出,针对小量渐变故障信息的检测,同样及时有效,检测延时32 s,漏警时长25 s。故障检测结果较好,验证了本文所提算法的有效性。
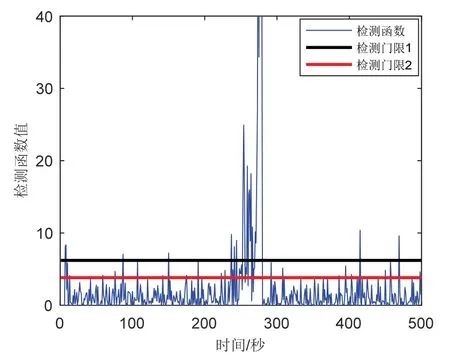
图14 AR 建模的残差χ 2检验Fig.14 The residualsχ 2test for AR modeling
4 结论
在组合导航系统故障检测过程中,针对组合导航系统渐变故障发生情况,本文提出了一种基于AR建模的组合导航渐变故障双阈值检测方法。该方法通过AR 量测建模,降低了量测污染分布导致的系统“跟踪”故障问题的发生,提高了系统的检测灵敏度。搭建双阈值检测门限,降低了漏警率对数据可靠性的影响。仿真试验结果表明,该方法针对无故障条件、突变故障条件情况下的检测效果仍然有效,特别是针对系统渐变故障发生时,有效提高了故障检测灵敏度和准确性,验证所提算法的有效性,对于组合导航系统故障检测及容错处理具有一定的参考价值。

