基于最小均方算法的半球谐振子特征参数辨识方法
郜中星,徐睿东,张勇刚
(1.哈尔滨工程大学物理与光电工程学院,哈尔滨 150001;2.哈尔滨工程大学智能科学与工程学院,哈尔滨 150001)
半球谐振陀螺(hemispherical resonator gyro,HRG)是一种基于科氏效应的固体波动陀螺,在高精度、高可靠性和抗辐射等方面具有突出的优势[1],可以满足军用领域和民用领域的多种传感需求。半球谐振子(hemispherical shell resonator,HSR)作为半球谐振陀螺的核心元件,其各向异性的程度与工作在全角模式下的陀螺性能密切相关。半球谐振子周向的刚度分布不均匀,会导致驻波的波形绑定和频率裂解现象,而周向的阻尼(或品质因数)分布不均匀,会导致驻波方位角向阻尼较小的方向漂移并自锁[1]。通常,用于表征半球谐振子的特征参数主要包括:刚度各向异性Δω,刚度失准角,阻尼各向异性 Δ(1 /τ),阻尼失准角[2]。目前,可以通过离子束或激光调平等方法将刚度分布不均匀抑制到最小程度(可小于0.5 mHz),但残余的频率裂解仍会对陀螺的灵敏度等性能产生影响。而阻尼分布不均匀目前尚缺乏有效手段进行处理,因此成为了制约全角半球谐振陀螺精度提升的关键因素[3,4]。综上,对半球谐振子的四种特征参数进行辨识不仅可以为陀螺的性能评估提供参考,还可以为全角半球谐振陀螺漂移误差和标度因数误差的补偿提供依据。
S.L.Li 等[5]提出了根据驻波进动效应的周期来求解半球谐振子频率裂解的方法,但求解的分辨率和有效性会受到半球谐振子品质因数的制约。I.P.Prikhodko 等[6]研究了在全角半球谐振陀螺中由阻尼各向异性引起的角度漂移会随着外界输入转速的增加而呈现线性减小的现象,并提出了通过高速虚拟旋转来减小阻尼各向异性的影响。P.Taheri-Tehrani 等[7]提出了利用非理想谐振子振动方程来求解阻尼各向异性Δ(1 /τ)的方法,但该方法需要将化简后的振动方程与角度测试数据进行拟合来提取 Δ(1 /τ),因而会引入较全文的结构安排如下:首先,根据非理想半球谐振子在椭圆坐标系下的运动方程,对全角半球谐振陀螺的工作原理和控制系统进行了介绍;然后,根据非理想半球谐振子的正交误差方程和驻波方位角误差方程,构建了基于LMS 算法的特征参数辨识模型;最后,基于Simulink 工具箱搭建了全角半球谐振陀螺的多参数仿真平台,利用该平台仿真验证了所提出辨识方法的有效性。
1 全角半球谐振陀螺的工作原理和控制系统
理想条件下,半球谐振子可以等效于进行简谐运动的质点。然而,真实系统中会存在由各向异性引起的刚度和阻尼耦合误差项,因此对非理想的半球谐振子在直角坐标系下的运动方程进行如下描述[9]:
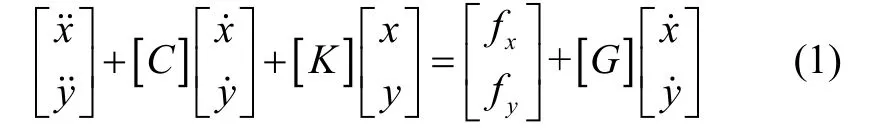
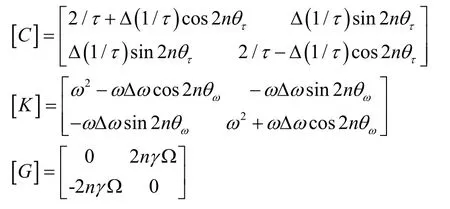
式(1)中,x和为谐振子在x模态上的位移和驱动力,y和为谐振子在y模态上的位移和驱动力。Ω 为外界输入的角速度,0.27γ≈为谐振子的进动因子,2n=为振型阶数。大误差。Z.X.Hu 等[8]提出了采用扩展卡尔曼滤波(EKF)来对半球谐振子特征参数进行估计的方法。该方法虽然具有较高的识别精度,但EKF 算法对样本数据的稳定性要求很高,因此需要半球谐振子具有很小的各向异性才能估计准确。综上,通过简单有效的方法快速估计出半球谐振子的特征参数,对于陀螺误差的补偿以及性能的提升将具有重要意义。
本文提出了一种基于最小均方(least mean square,LMS)算法的半球谐振子特征参数辨识方法。
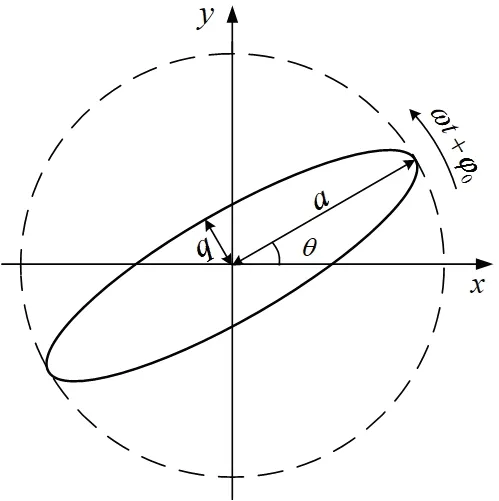
图1 二维谐振子的运动轨迹Fig.1 Motion trajectory of the two-dimensional resonator
二维谐振子的运动轨迹如图1所示[10],在科氏力作用下半球谐振子的振型相对于安装基座以γ-Ω 的角速度围绕中心反向旋转。根据图1,x模态轴与y模态轴上的位移表达式为:
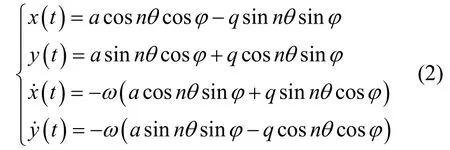
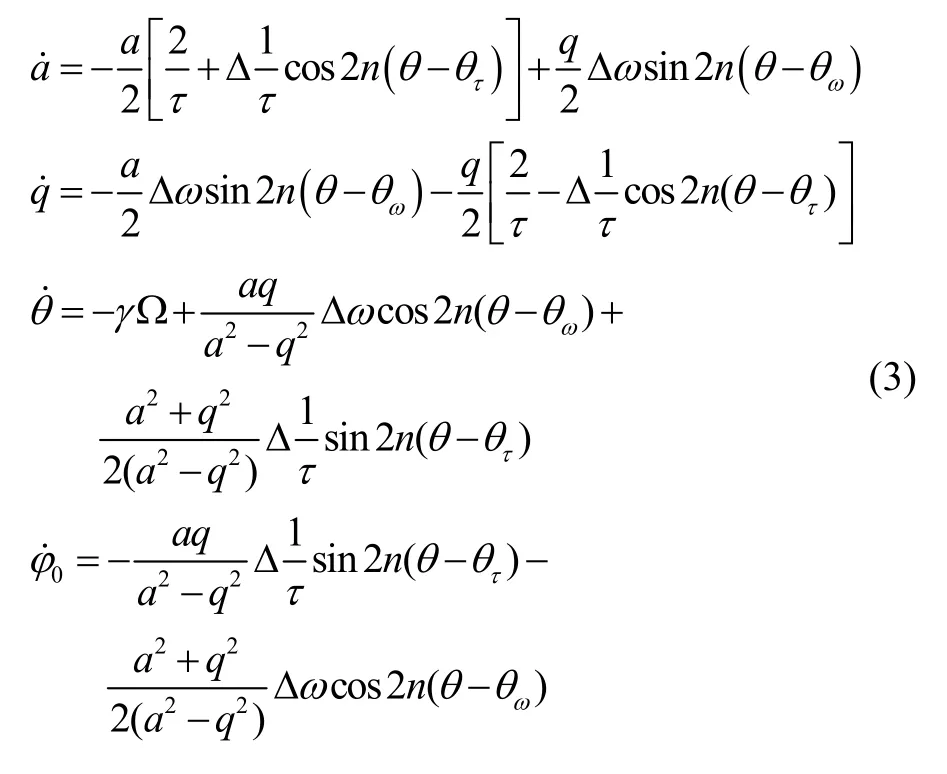
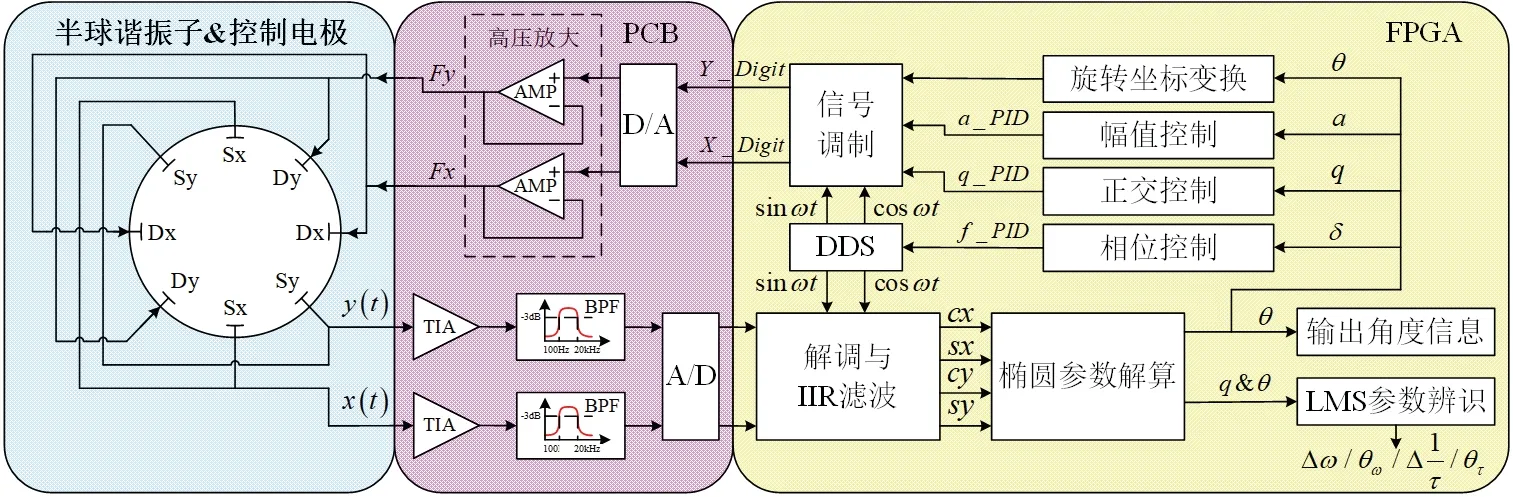
图2 全角半球谐振陀螺的控制系统框图Fig.2 Block diagram of HRG control system with whole-angle mode operation
全角半球谐振陀螺的控制系统框图如图2所示。为了提高检测信号的信噪比,模拟前端使用了跨阻放大、带通滤波等方法对检测信号进行处理。将处理后的检测信号与DDS 产生的参考信号进行乘法解调,经过IIR 滤波后得到用于椭圆参数解算的四个有效信号分别为:cx、sx、cy、sy。再代入到参数解算方程(4)中分别得到半球谐振子的椭圆参数为:a、q、θ、δ[12]。
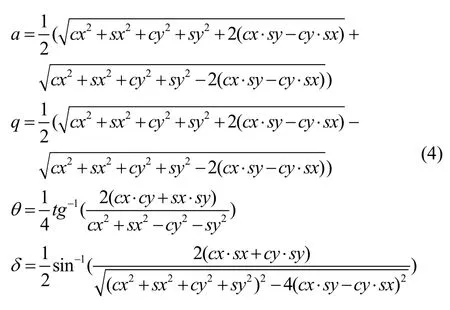
其中,通过对θ进行旋转坐标变换来实现驱动力与驻波方位角的对准;通过对a进行PID 幅值控制产生 _a PID信号来维持振幅稳定;通过对q进行PID 正交控制产生 _q PID信号来抑制正交误差;通过对δ进行PID 相位控制产生 _f PID信号来保证参考信号与检测信号的相位差恒定。对以上四个环节的输出信号通过调制产生驱动信号,最后将驱动信号施加到驱动端电极可以得到驱动力信号Fx,Fy。以上各个环节共同构成了全角半球谐振陀螺控制系统的一个完整信号环路。
2 基于LMS 算法的特征参数辨识模型建立
非理想半球谐振子在椭圆坐标系下的正交误差方程为式(5)所示。
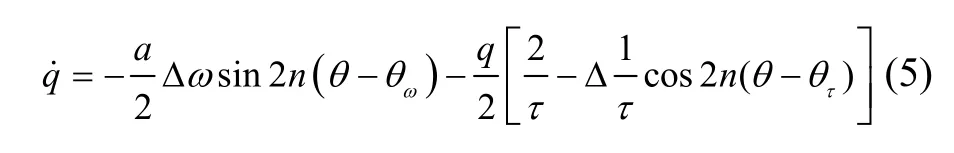
对陀螺不施加正交控制,虽然此时q不为0,但正交信号仍远小于幅值信号即q a≪,则式(5)可以简化为式(6)的形式。可以看出,式(6)仅含有半球谐振子特征参数中Δω和的信息,避免了参数辨识过程中与 Δ(1 /τ)和产生耦合。
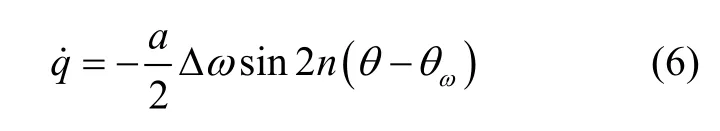
将式(6)进一步展开可以得到:
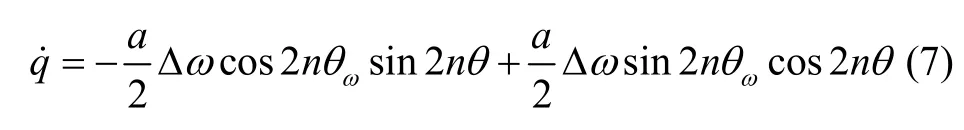
下面,基于LMS 算法构建关于ωΔ 和的参数辨识模型,令:
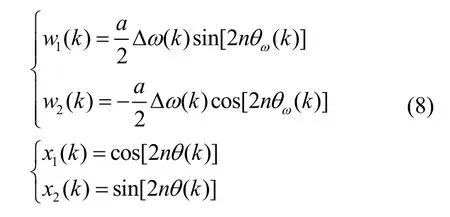
则可以得到:
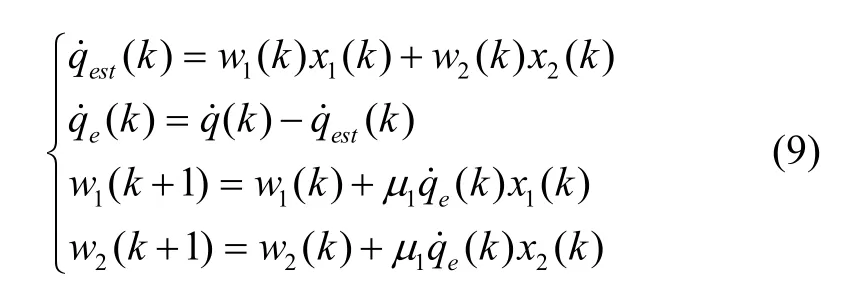
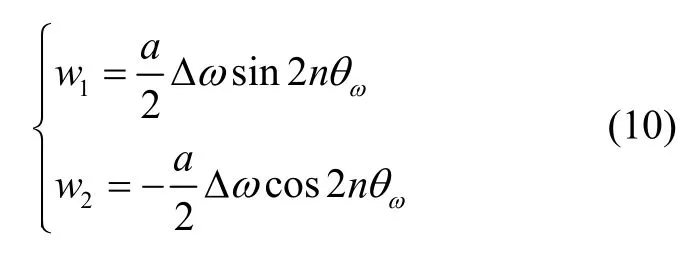
根据式(10)的估计结果,可以得到刚度各向异性ωΔ 和刚度失准角的辨识结果分别为:
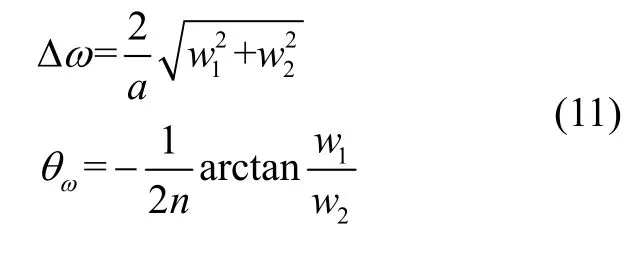
非理想半球谐振子在椭圆坐标系下的驻波方位角误差方程如式(12)所示。
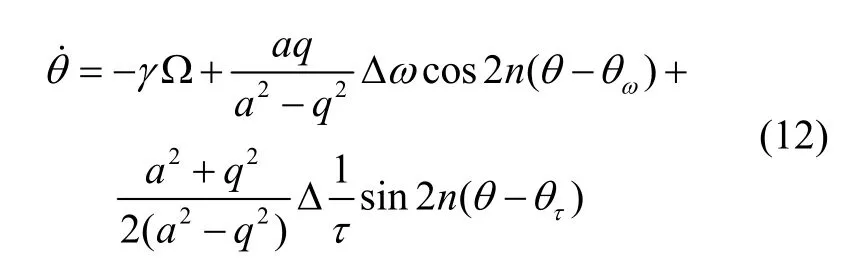
对陀螺施加正交控制,此时q被抑制到0,则式(12)可以简化为式(13)的形式。可以看出,式(13)仅含有半
球谐振子特征参数中(1/)τΔ和的信息,避免了参数辨识过程中与ωΔ 和产生耦合。
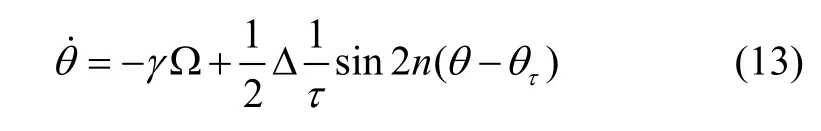
将式(13)进一步展开可以得到:
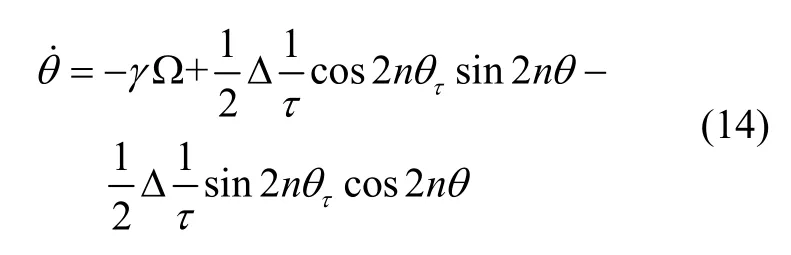
下面,基于LMS 算法构建关于(1/)τΔ和的参数辨识模型,令:
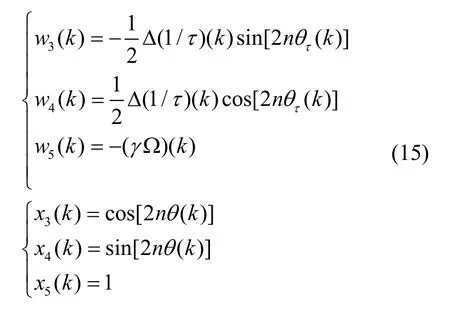
则可以得到:
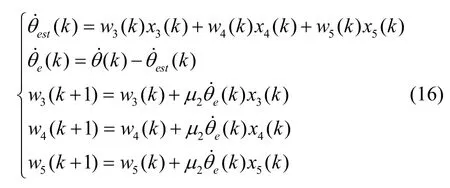
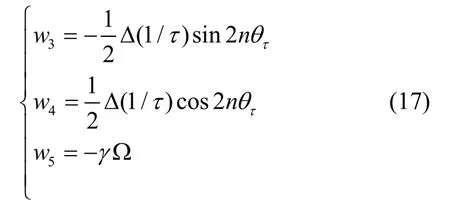
根据式(17)的估计结果,可以得到阻尼各向异性Δ(1/τ)和阻尼失准角的辨识结果分别为:
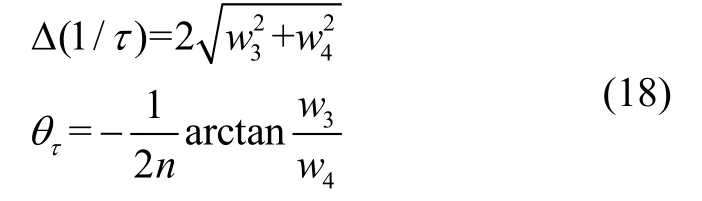
式(5)-(18)给出了基于LMS 算法对半球谐振子进行特征参数辨识的过程,通过优化以及转速激励Ω 的选择,可以进一步提高辨识精度和辨识速度。
3 仿真验证与结果分析
为了验证所提出的特征参数辨识方法的有效性,利用Simulink 工具箱搭建了全角半球谐振陀螺的多参数仿真平台,如图3所示。通过不同的参数设定,可以仿真分析半球谐振子的各种运动规律。其中:非理想半球谐振子模块包含了式(1)中需要辨识的四种特征参数;电容检测模块包含了C/V 转换、带通滤波与A/D 转换;信号解调模块包含了参考信号与检测信号的乘法解调和数字低通滤波器;椭圆参数解算模块用于半球谐振子椭圆参数a、q、θ、δ的解算;信号调制模块包含了幅值控制、正交控制、相位控制以及旋转坐标变换;最后,静电驱动模块包含了D/A 转换与高压放大。
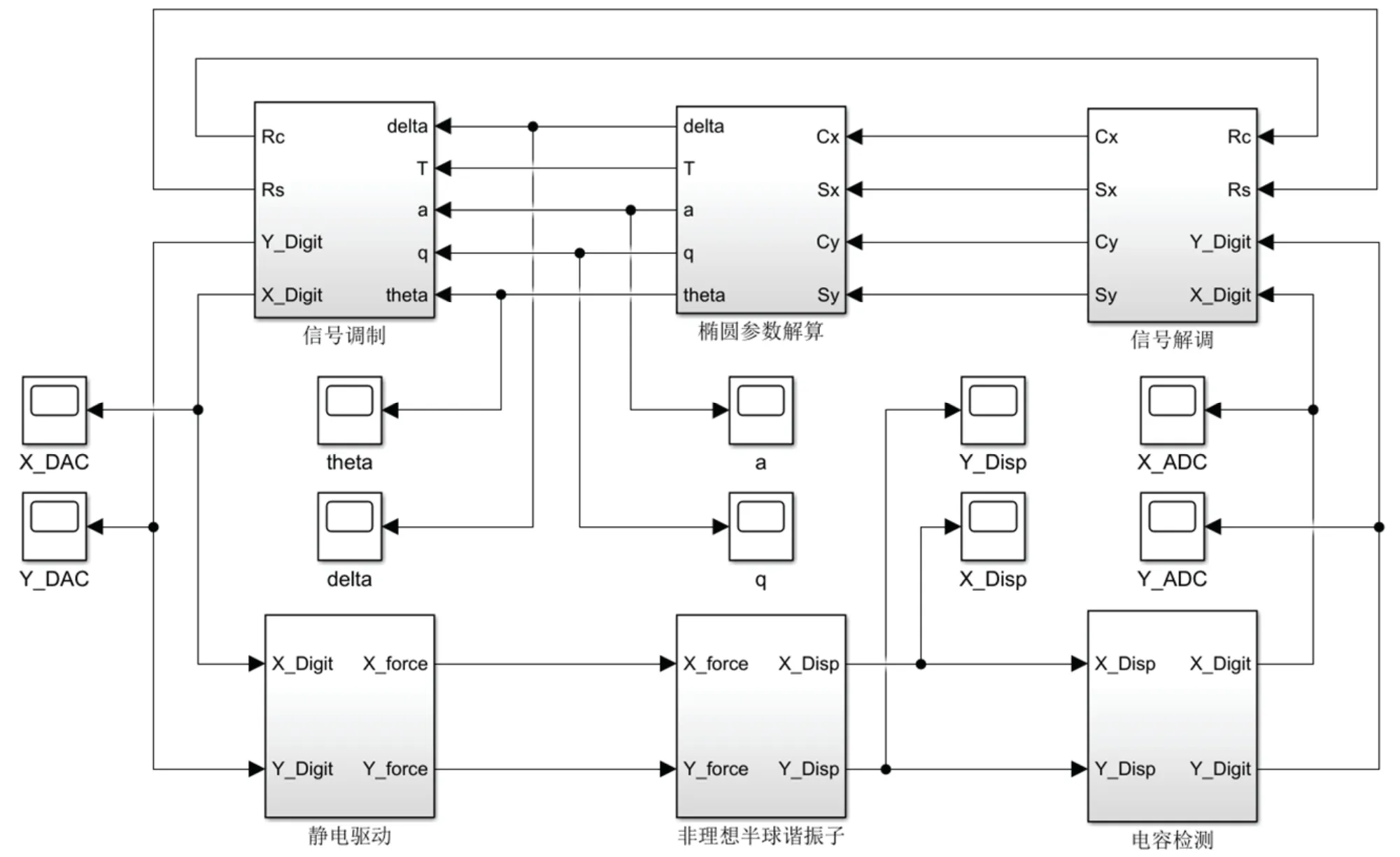
图3 全角半球谐振陀螺仿真模型Fig.3 Simulation model of HRG with whole-angle mode operation
表1 列出了用于验证所提出辨识方法的转速激励条件和半球谐振子特征参数。可以计算得到对应的Δω和 Δ(1/τ)分别为:。
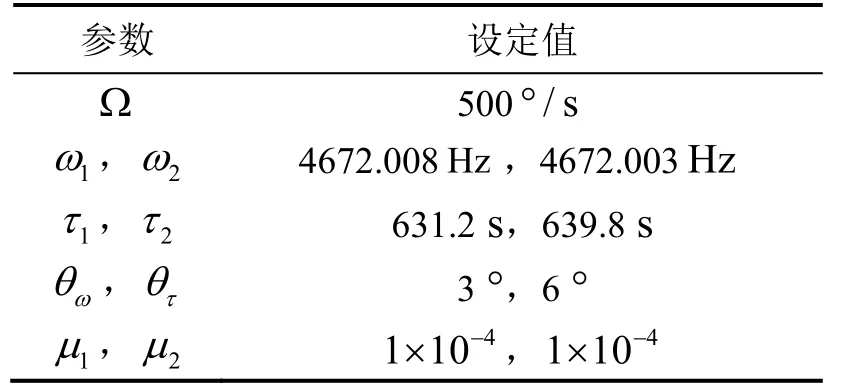
表1 仿真参数设置Tab.1 Simulation parameters of HRG
通过图3所示的Simulink 程序得到正交分量q的数据集和驻波方位角θ的数据集,同时利用所提出的基于LMS 算法的辨识模型,图4 和图5 分别给出了半球谐振子特征参数的辨识结果。可以看出,半球谐振子的四个特征参数全部在8 s 以内辨识出来,并且全部收敛于设定值,从而仿真验证了所提出方法的有效性。通过优化LMS 的算法步长,可以实现更精确、更快速的辨识。
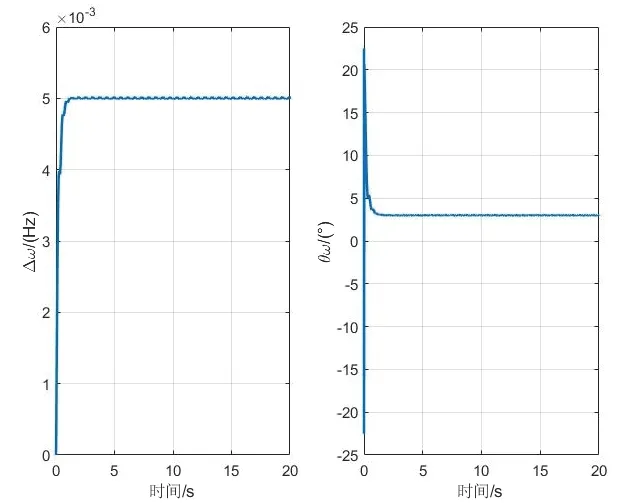
图4 ωΔ 和的辨识结果Fig.4 Identification results of ωΔ and
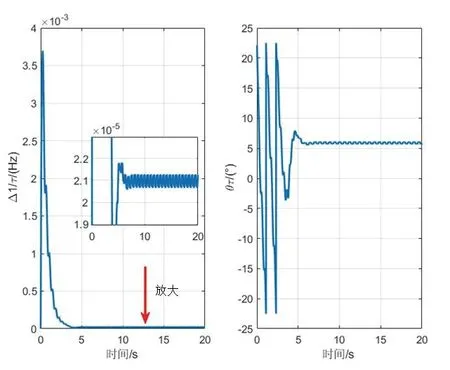
图5 和的辨识结果Fig.5 I dentification results of and
4 结论
本文根据非理想半球谐振子在椭圆坐标系下的正交误差方程和驻波方位角误差方程,构建了基于LMS算法的半球谐振子特征参数辨识模型。根据全角半球谐振陀螺工作原理,基于Simulink 搭建了全角半球陀螺控制系统的仿真平台。仿真结果表明,所提出的辨识方法能在8s 内辨识出半球谐振子的刚度各向异性、刚度失准角、阻尼各向异性和阻尼失准角,从而实现了快速且准确的特征参数辨识。下一步的工作将会利用半球谐振陀螺实际采集的数据集对所提出的参数辨识方法进行实验验证,同时研究特征参数的在线辨识方法,从而实现半球谐振陀螺输出误差的实时校准与补偿。

