基于改进序列凸优化的固体火箭入轨制导方法

王洪波，张若男，梁 卓，吕 瑞

（中国运载火箭技术研究院，北京 100076）

耗尽关机固体运载火箭的推力大小和工作时间无法主动控制，如何利用有限速度调节能力实现高精度入轨，是当前国内外固体火箭制导领域研究热点。凸优化算法有确定收敛性、求解快速的优点，能够满足多飞行阶段固体运载火箭的在线规划和制导要求。

文献[1][2]利用凸优化方法解决火箭上升动力段入轨制导问题，其发动机推力可调，末端关机时间可控；文献[3]使用凸优化方法寻找火箭上升段推力下降故障时最优圆轨，但其只作为后续迭代初值，未严格考虑终端约束；文献[4][5]针对运载器回收制导问题，构建多阶段二阶锥规划模型，利用序列凸化算法离散求解；文献[6]建立了有限推力远程轨道转移问题的凸优化模型，利用迭代逼近验证凸优化算法在远程轨迹规划问题中的可行性。

基于此，本文研究耗尽关机固体火箭入轨制导问题，建立含推力方向和终端入轨参数约束的“滑行段+动力段”运动模型。使用拉道（Legendre–Gauss–Radau，LGR）伪谱法离散滑行段运动模型，将点火时间增广为新的控制变量；将推力方向非凸球面可行域松弛为凸球体可行域。并从理论上证明松弛的无损性，同时对运动方程和终端等式约束进行线性化，构建凸优化子问题；利用含初值生成器的序列凸优化算法迭代逼近原问题，得到最优滑行时间和最优推力矢量，实现耗尽关机固体火箭动力段能量管理，最终高精度入轨。

1 固体火箭多阶段入轨制导模型

1.1 最优控制问题描述

本文所研究的固体子火箭入轨制导问题，飞行高度大于100 km，处于大气层外，不考虑气动影响[7]。动力段发动机推力为常值，火箭推力方向与箭体纵轴重合，姿态控制视作理想环节；飞行采用“滑行+动力”方案，在地心惯性系下建立的三自由度运动模型：

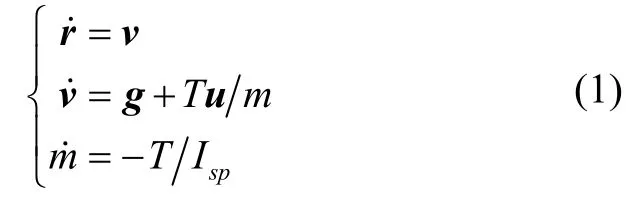
式中，状态量r、v、m分别为坐标系下位置、速度和质量；g为火箭重力加速度：

Isp为发动机比冲；T为发动机推力，滑行段发动机推力为零，动力段发动机推力为不可调常值[8]，u为推力方向单位矢量：

设滑行段开始时间为t0=0，滑行段结束（动力段开始）时间为ts，终端时间为tf。

目标轨道为圆轨道，发动机燃料耗尽关机时，火箭需满足目标轨道约束：

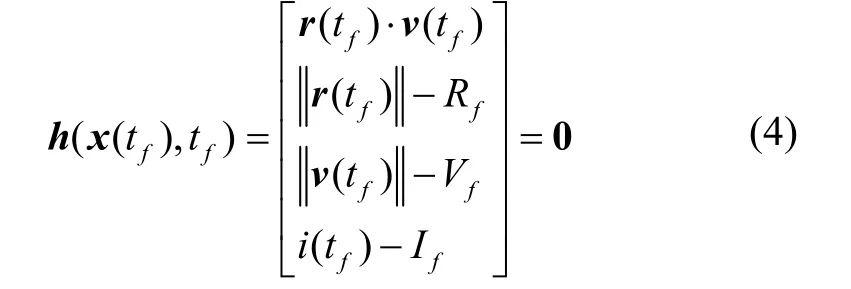
其中，Rf、Vf、If分别为目标轨道地心距、轨道速度和轨道倾角。

实际飞行中，长时间滑行中姿态调整将给姿控系统带来不利影响，因此选择飞行时间作为需要优化的性能指标：

综上，固体火箭入轨段最优控制问题为式(1)-(5)。

该入轨制导问题分为滑行与动力两阶段，各段内状态与控制量变化连续。由于滑行段时间较长，为了获得较高的离散精度，采用收敛速度较快的LGR 伪谱法离散[9]；动力段时间相对较短，采用一阶保持器的等距离散。

1.2 滑行段离散建模

LGR 伪谱法配点定义在[-1，+1)之间，将原问题时域映射至[-1，+1)区间内，如式(6):

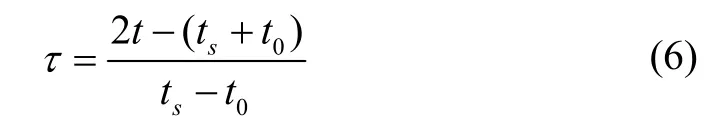
式中，τi(i=1...N1)是[-1，+1)上的N1阶Legendre多项式零点。τs=+1 和τi(i=1...N1)构成N1+1个插值点。

为表述方便，以τ为变量的状态量与控制量仍旧使用x、u表示，状态量及其导数的插值近似为：

式中Li(i=1...N1+1)为Lagrange 插值基函数。

滑行段动力学方程离散模型如下：

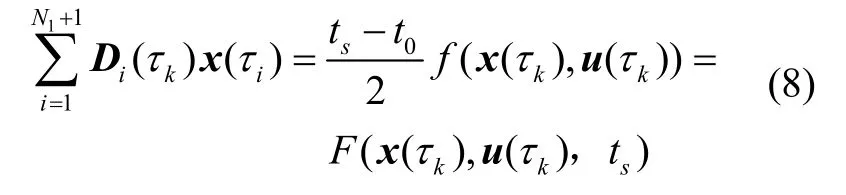
式中，D为N1×(N1+1)阶微分矩阵，f(x(τk),u(τk))为动力学微分方程(1)的右端函数，其中发动机推力T=0。

滑行段初始状态已知：

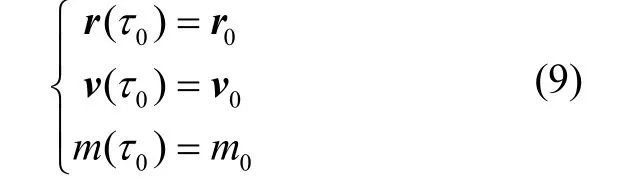
1.3 动力段离散建模

动力段设置N2个离散点，离散时间间隔为：

采用一阶保持器的动力段均匀离散模型如下[10]：

动力阶段有式(3)所示推力矢量约束。飞行过程中状态量连续，阶段间连接约束为：

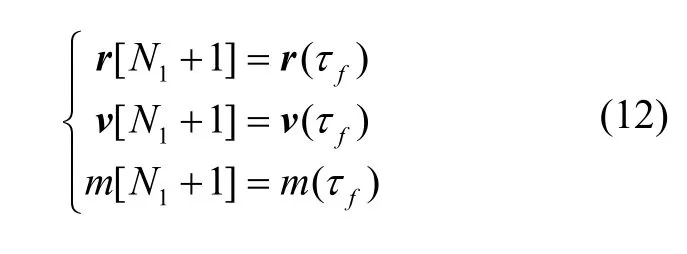
因为火箭发动机耗尽关机，终端约束除式(4)的入轨条件外还有终端确定质量约束：

通过上述分段离散，控制量加入发动机开机时间ts，解决了终端时间不确定问题，将经过离散后的模型称为问题1。

2 推力方向约束无损凸化

问题1 中动力段推力大小恒定，推力矢量等式约束为球面非凸可行域，对该约束进行无损凸化，即将问题的非凸可行域进行适当松弛放大构成新的凸可行域，针对本文形成的球面可行域进行如下松弛变换：

仅当式(14)取等号时该约束为积极约束，与原问题等价。通过庞特里亚金提出的极大值原理可证明，松弛后问题最优解仍满足原问题可行域约束，即松弛后子问题最优控制分量时刻满足。

本文所研究的固体运载火箭，其推力大小不可调节，动力段质量变化与状态量和控制量无关，在每个制导周期内质量为常量，在整个动力段线性时变[11～13]，因此证明中将质量看作常量，同时需要增加动力段时长等式约束,ΔTburn为动力段发动机工作时长。

模型描述：

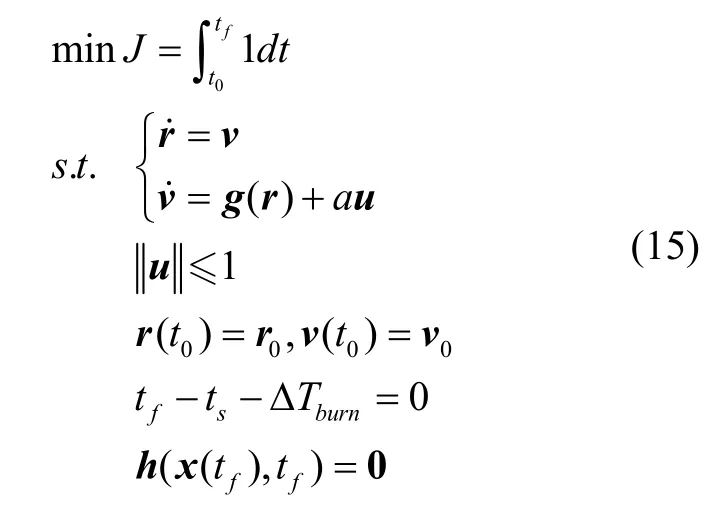
证明：

松弛后最优控制问题的哈密顿函数：

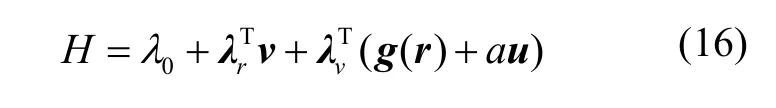
最优控制问题存在终端状态和时间约束，终端函数为：

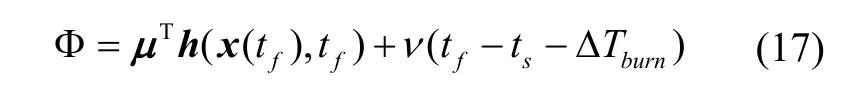
协态方程：

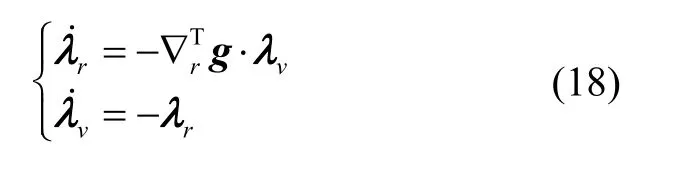
极大值条件：

控制约束松弛条件：

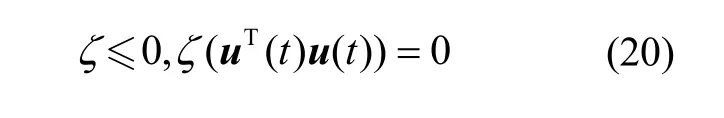
由于终端时间受约束，哈密顿函数：

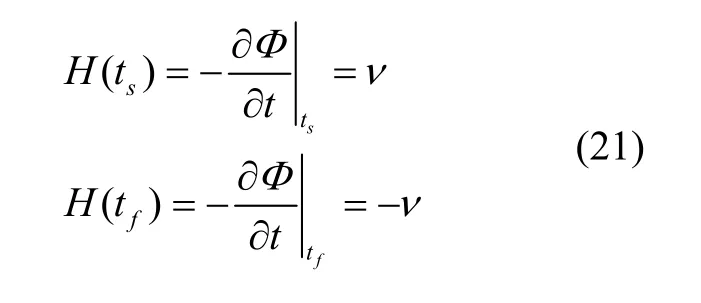
根据终端函数可知哈密顿函数跳变条件：

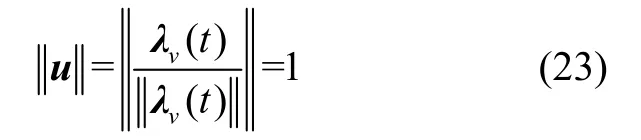
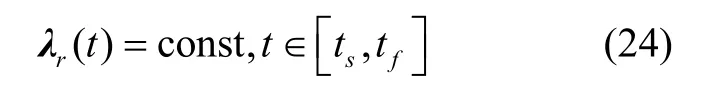
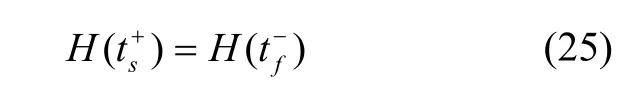
将式(22)中两式相加，并结合式(25)可得：

又因该最优控制问题末端时间自由，终端时刻哈密顿函数为零，即：

由式(26)可知：

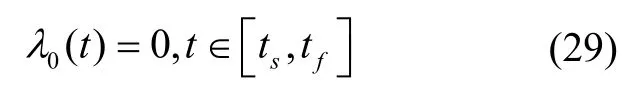
3 序列凸优化算法

问题1 非凸性除了推力分量约束形成的球面可行域外，还有非线性动力学方程和终端入轨非凸等式约束。利用线性化方法，问题1 将转化成二阶锥规划问题，继而可利用凸优化算法求解。

3.1 动力学方程线性化

针对非线性动力学方程中的非凸约束，通过在上一次迭代结果处进行一阶泰勒级数展开，将其转化成凸约束，通过迭代，结果将逐渐逼近原问题最优解[14]。

问题1 中滑行段动力学方程左端矩阵D是常数矩阵，将右端增广非线性函数进行一阶泰勒级数展开：

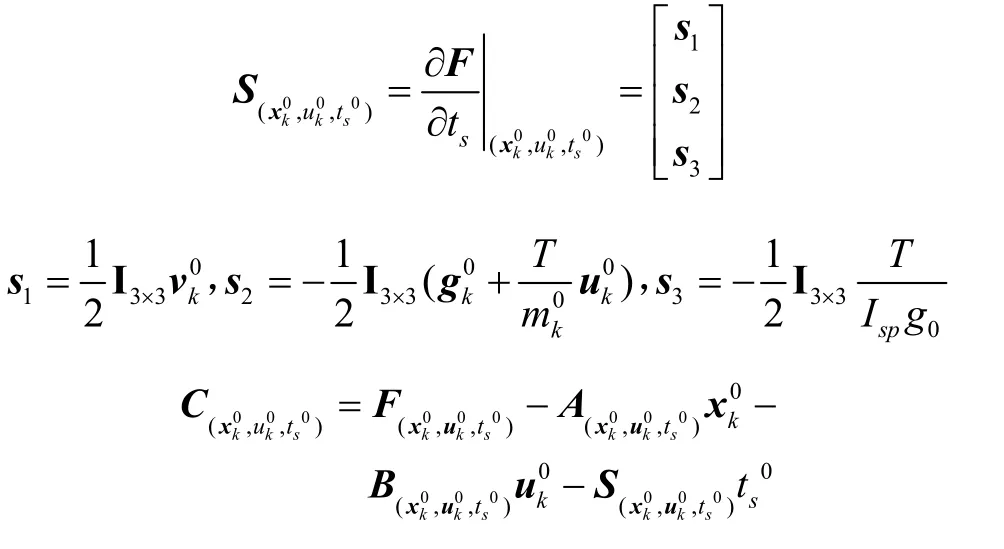
动力段运动方程进行一阶泰勒级数展开，形式与滑行段类似。

3.2 终端约束线性化

运载火箭入轨时终端约束为关于状态的非线性非凸等式约束，在终端时刻对式(4)进行一阶泰勒级数展开：

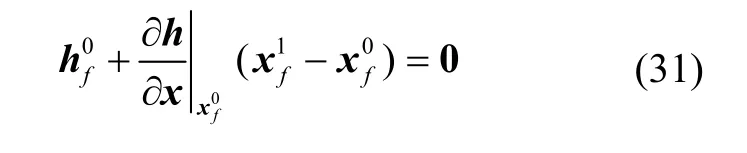
3.3 序列凸优化问题及其求解

问题1 经过线性化和无损松弛，得到序列二阶锥规划问题：

1）松弛因子

经过上述凸化后的子问题，称为问题2，在迭代求解初期，由于线性化产生的偏差，可能会造成“伪不可行”，即原问题存在可行解，但线性化后问题不可行。因此对问题2 中动力学方程（以滑行段为例）和终端约束添加松弛因子[15]：

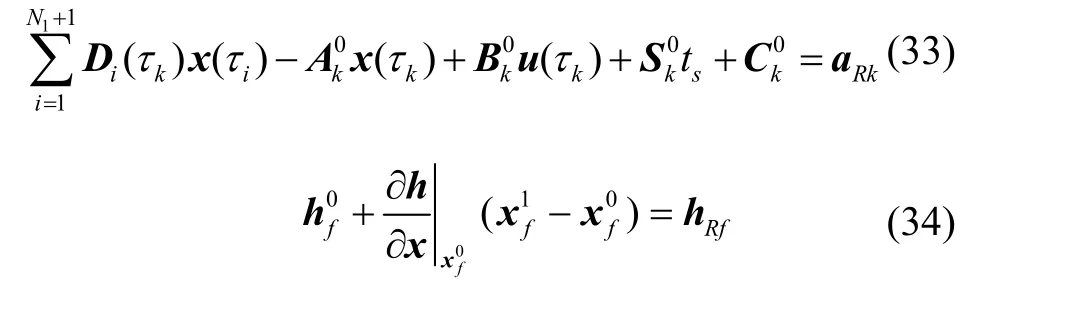
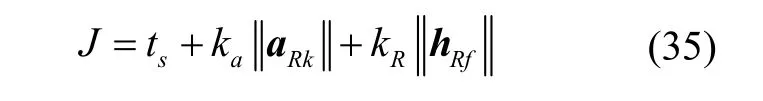
2）信赖域

利用序列凸优化算法对问题2 迭代求解时，每一次都选择上一次迭代结果作为本次泰勒展开参考点，因此前后两次求解结果必须满足小偏差约束，否则会导致子问题线性化带来误差过大从而迭代失败。引入第i次和第i+1 次变量迭代结果的信赖域约束：

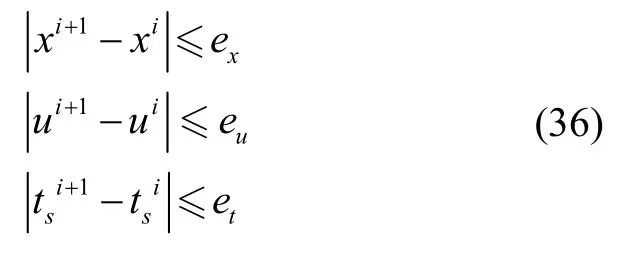
3）初值生成

迭代开始需提供初始状态序列，良好的初始轨迹有利于迭代的快速收敛[16,17]。本文所研究的入轨问题末端状态受等式约束，设计如下初值生成策略：首先选择点火时间初值，在动力段，令俯仰角为时间的线性函数，偏航角恒定，得到姿态角曲线为：

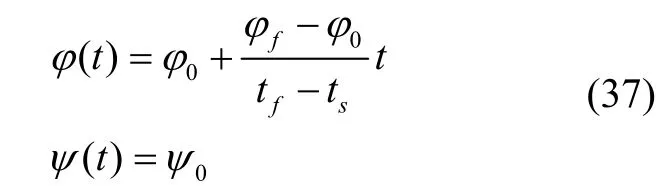
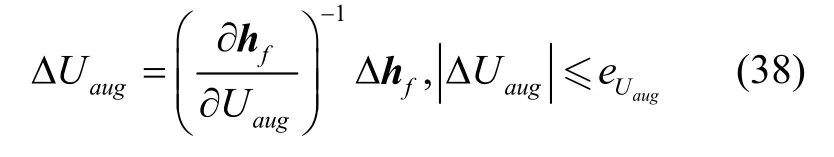
4 仿真校验

选择某固体运载火箭的第三级子火箭作为仿真对象，使用改进序列凸优化算法和LGR 伪谱法，对比说明本文所提出的改进序列凸优化算法的有效性和高效率。火箭发动机参数如表1所示，地心惯性系下初始状态和终端入轨约束如表2所示，目标轨道为圆轨。

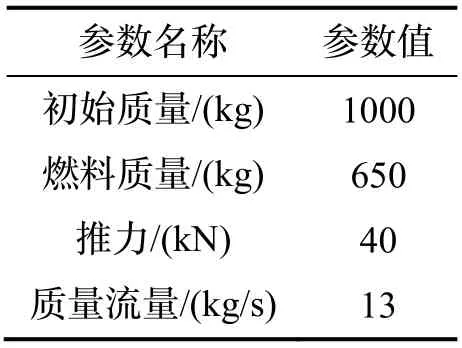
表1 火箭参数Tab.1 The rocket parameters

表2 初始状态和终端约束Tab.2 Initial state and terminal constraints

本文数值计算在i7 3.6 GHz 笔记本电脑下进行，程序均在MATLAB 2014a 环境下编译运行，采用CVX工具箱和SDPT3 求解器进行解算。

4.1 仿真结果

滑行段设置40 个LGR 离散点，动力段设置20个离散点，火箭滑行段时长作为性能指标，优化得到滑行时间为160.2 s，动力飞行50.0 s。

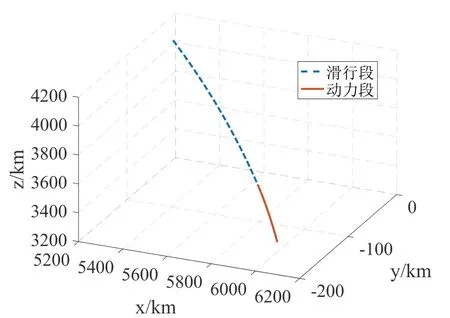
图1 滑行+动力段三维轨迹Fig.1 Three dimensional trajectory of sliding and power segments

图2 地心距随时间变化曲线Fig.2 Geocentric distance curve over time

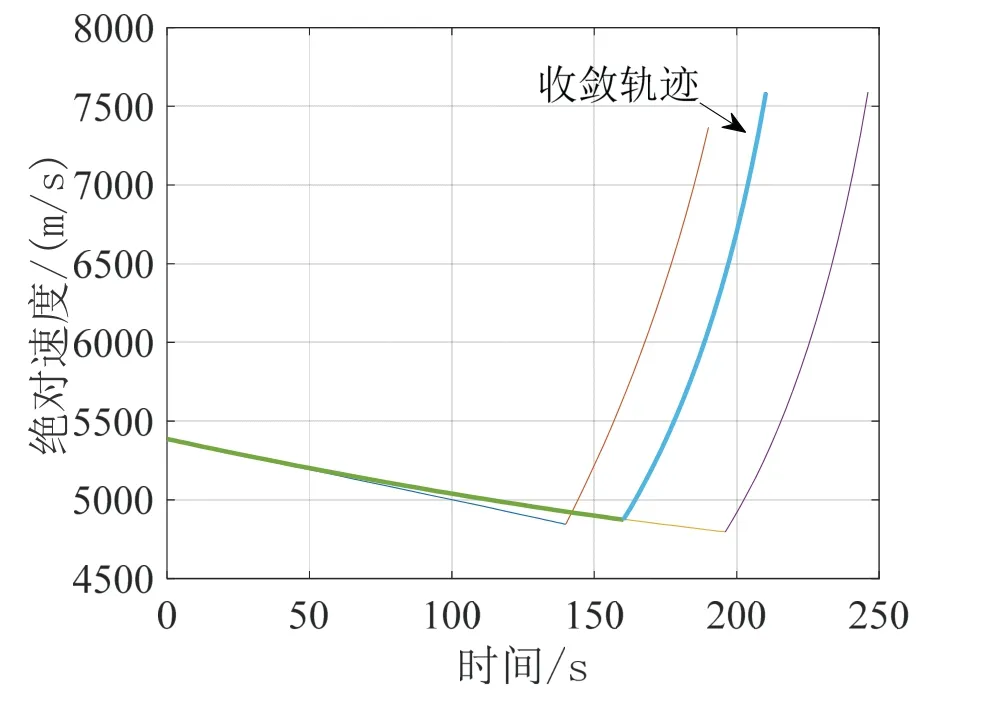
图3 速度随时间变化曲线Fig.3 Velocity curve over time

图1是改进序列凸优化算法迭代得到的三维轨迹，图2、3分别为各次迭代得到的飞行过程中地心距和速度变化曲线，最终得到的满足收敛误差阈值的轨迹在图中标出。火箭耗尽关机时，满足终端轨道约束。

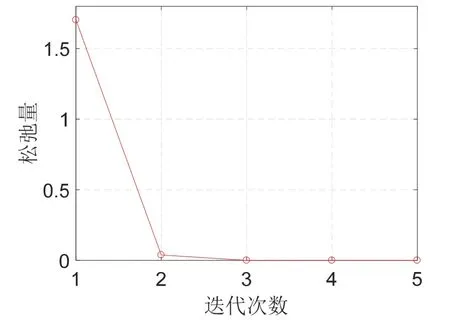
图4 松弛量变化曲线Fig.4 Relaxation curve

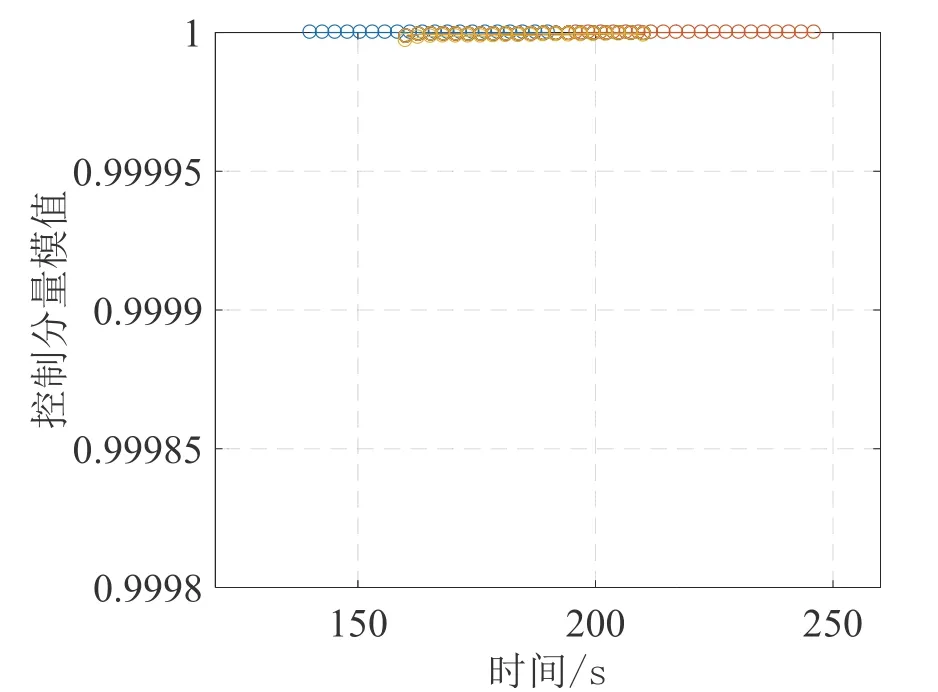
图5 推力方向模值变化曲线Fig.5Thrust vector modulus curve

图4中松弛因子随迭代次数增加趋近于0，最终小于10-9，说明序列凸化求解结果与原问题最优解等价性。图5为动力段推力方向模值，可以发现始终满足，验证结论1。

4.2 求解精度与效率分析

使用本文提出的初值生成器，耗时0.12s构建初始轨迹，得到的初始轨迹滑行时长为155.72s，终端地心距误差为0.6km，终端入轨速度误差为21.76m/s，终端当地速度倾角误差为0.056 rad，终端轨道倾角误差为0.0071rad。改进序列凸优化算法优化后的终端地心距误差为0.22m，速度误差为-0.063m/s，当地速度倾角误差为0.00047rad，轨道倾角误差为-0.00023rad，火箭成功入轨，验证本文提出的改进序列凸化方法的可行性。

图6-7为采用序列凸优化算法和伪谱法求解得到地心距、速度变化曲线对比，两种方法计算结果吻合，说明本文所提的改进序列凸优化算法在实现高精度入轨上的有效性。

图6 凸优化方法和伪谱法地心距变化Fig.6 Geocentricvariation by convex optimization and pseudospectral method

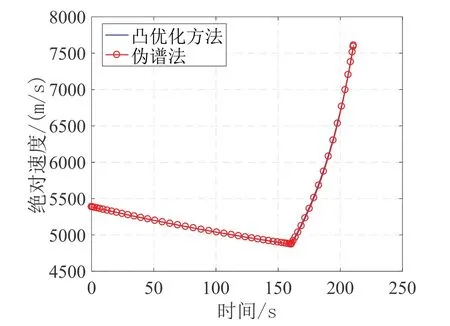
图7 凸优化方法和伪谱法速度变化Fig.7 Velocity variation by convex optimization and pseudo spectralmethod

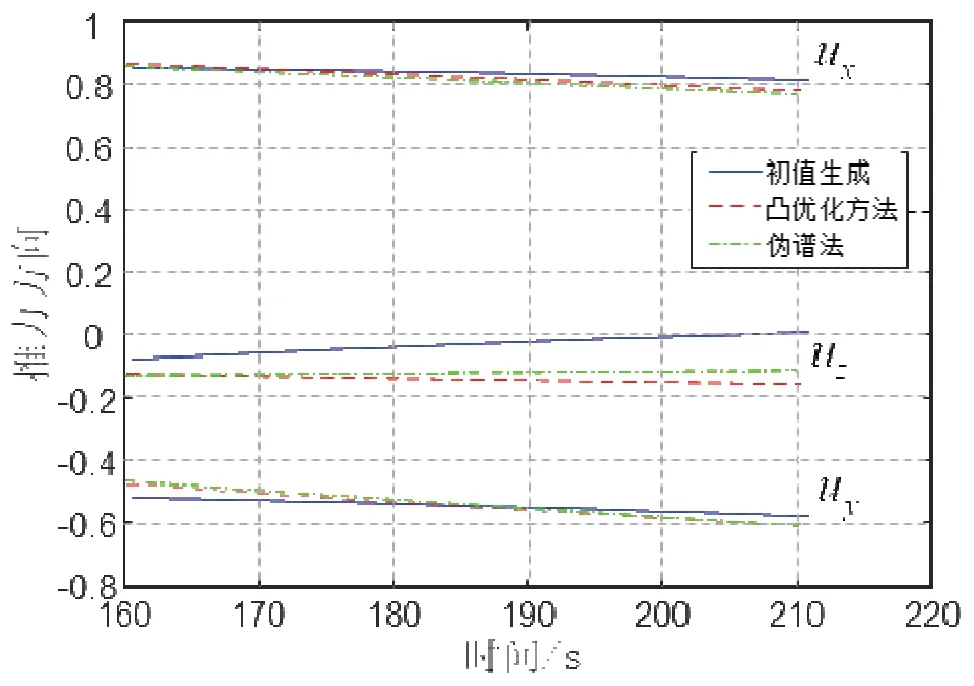
图8 凸优化方法和伪谱法控制分量变化Fig.8 Thrust vector by convex optimization and pseudo spectralmethod

图8为分别采用初值生成器、凸优化方法和伪谱法得到的发射惯性坐标系下动力段发动机推力方向曲线，可以发现凸优化方法和伪谱方法仿真得到结果基本吻合。

采用改进序列凸优化算法经过5次迭代结果收敛，每次迭代中求解凸优化子问题单步CPU 时间平均为0.16 s，模型初始化到得到收敛结果共耗时7.96 s，而伪谱法耗时118.42 s，改进序列凸优化算法计算效率相较于LGR 伪谱法,求解时间缩短了93.2%，具有显著优势。

5 结论

本文针对耗尽关机固体运载火箭入轨段制导问题，提出一种改进序列凸优化算法，以滑行段时长为优化指标，规划点火时间和动力段推力方向，实现火箭耗尽关机时精确入轨，通过仿真验证得到主要结论如下：

利用LGR 伪谱法进行时域映射，将发动机开机时间作为新的控制变量，解决了点火时间不确定问题，保证了滑行时长的最优性。

针对推力方向非凸球面约束，通过松弛转化为凸的球体约束，并在理论上证明松弛手段的无损性；将非凸的动力学方程和终端状态等式约束在参考轨迹上进行线性化，从而将其转化为凸约束，利用序列凸优化算法，结合松弛因子和信赖域等迭代策略，使构建的凸优化子问题最优解逼近原问题最优解。

含初始轨迹生成器的序列凸优化算法求解本文研究的入轨制导问题时间仅为伪谱法的6.72%，解算结果终端地心距误差为0.22 m，速度误差-0.063 m/s，当地速度倾角误差为 0.00047 rad，轨道倾角误差为-0.00023 rad，验证本文所提出的改进序列凸优化方法解决耗尽关机固体火箭入轨制导问题的有效性。