基于有限元分析方法的三浮陀螺用角度传感器优化设计

吴 辽，王建青，党建军，杜 鑫，黄 铭

（西安航天精密机电研究所，西安710100）

三浮陀螺仪因其精度高、体积小、寿命长等优点在卫星、航海等领域应用广泛。“三浮”指电机采用动压气浮、浮子组件采用液浮和磁悬浮。高速旋转的电机使浮子形成陀螺效应，输出轴在精密角度传感器和力矩器的闭环控制下完成陀螺力矩检测。其中角度传感器作为三浮陀螺的核心电磁元件，主要作用是敏感陀螺浮子在进动力矩作用下沿输出轴的微小角位移，角度传感器性能的提升是陀螺精度提高的关键技术。其中动圈式角位移传感器是常用的一种传感器，它是靠输出线圈相对激磁线圈之间角位移来改变它们之间的互感系数而形成输出电压信号。动圈式传感器的优点为结构简单、尺寸小，工作时无机械摩擦，寿命长，零位输出和非灵敏区均较小，它的缺点为输出功率小且因动圈有输电引线会产生引线干扰力矩。

随着惯性制导与导航技术的不断发展，以三浮陀螺为代表的机械式陀螺仪系统复杂、开发周期长的问题越来越突出，这就对电磁元件的设计模型和分析计算方法的精确性提出了更高的要求。在产品升级、方案迭代过程，要求动圈式角度传感器在不改变机械接口尺寸和激磁电源的情况下，灵敏度Kp提高30%，激磁电流I1变化不大于10%，零位电压小于5 mV，非线性度优于5%。一直以来，在动圈式传感器的设计中普遍采用场化路的计算方法，在理想条件下对磁场和磁路的情况进行了简化和假设，比如：（1）假设工作气隙内磁场分布均匀；（2）忽略铁芯磁阻；（3）不考虑漏磁通的影响。因此这种计算方法不能准确反映传感器的真实工作状况，设计方案往往需要多轮迭代，效率较低，很难在短期之内完成产品升级的任务[1-3]。

基于有限元分析方法在电磁元件设计方面有较高的效率和准确度，建立参数化模型，在接口尺寸和电气指标的约束下完成核心设计参数的遍历计算，给出满足要求的参数搭配关系，结合工艺性选择最优的设计方案。本文首先从变压器磁链方程出发推导建立了多级式动圈角度传感器的数学模型，分析灵敏度Kp、激磁电流I1的影响因素，结合生产工艺、尺寸、电气边界条件确定了激磁绕组N1、输出绕组N2、气隙长度lg和工作半径rp为设计变量，并给出了参数的取值范围，借助有限元仿真软件建立参数化模型进行设计参数遍历计算，给出最优设计方案，并通过了实物测试考核，验证了灵敏度Kp、激磁电流I1、零位电压、非线性度均满足设计输出的要求[4-7]。

1 动圈式传感器数学模型

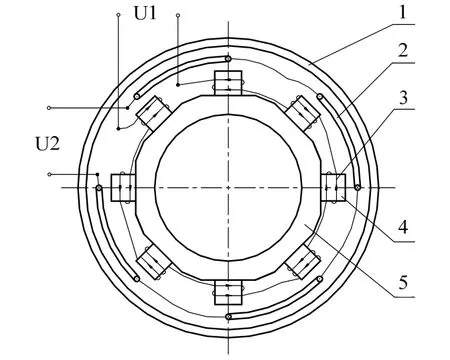
图1 多极动圈式传感器结构示意图Fig.1 Structure diagram of multi-pole moving coil sensor

动圈式传感器是基于变压器原理进行工作的，它由定子组件和动圈组件两部分组成。定子组件的作用是在工作气隙中建立所需的交流磁场，它由外导磁环、内导磁环、铁芯、激磁线圈和结构件组成。动圈组件由输出线圈组成的绕组和相应的结构件组成，其作用是输出与其转动角度成一定比例关系的交流电压信号。在三浮陀螺仪中采用的多极动圈式感应传感器，其结构如图1所示[7-9]。

在基于等值磁路的设计中，动圈式角度传感器与变压器输出特性相类似，假设磁通φ全部被约束在铁芯磁路中，则激磁线圈和输出线圈内产生的感应电动势e1和e2为：

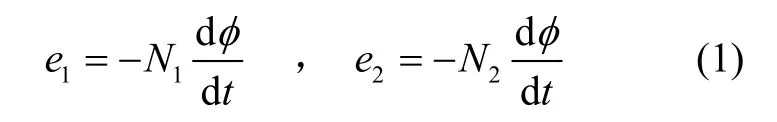
激磁线圈的电阻压降为i1R1，则激磁线圈和输出线圈的电压方程为：

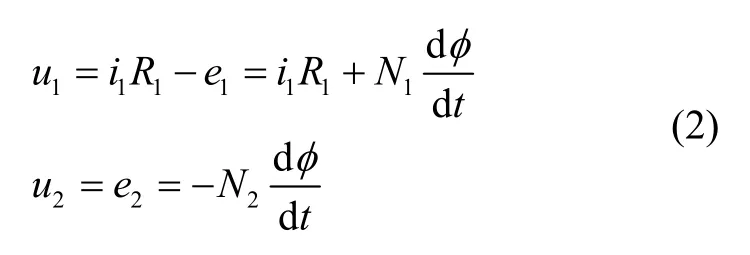
u1、u2为激磁电压和输出电压的瞬态值、U1、U2为对应的有效值，N1、N2为激磁线圈和输出线圈匝数，磁通计算关系为：

A为有效磁路面积，lg为气隙长度，μ0为气隙磁导率，其值为 4π×10-7H/m，考虑到电流的正弦性为激磁电流的有效值、f为激磁频率，将式(2)代入式(3)中可得：

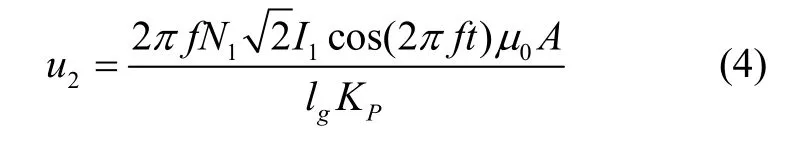
式(4)为常见的互感式变压器输出方程，但不适用于图1所示的多极式动圈角度传感器的输出，主要原因为有效磁路面积计算方式不同，为了消除共模干扰，动圈式角度输出线圈采用了串联反接的方式，转动角度α为零的情况下有效磁路面积A为零，传感器无输出。有效面积和转动角度表达关系式为：

其中，mp为磁极数，图1所示结构为4 极，rp为动圈有效旋转半径，lp为输出线圈有效边长。将式(5)代入式(4)即得到了动圈式角度传感器的输出电压表达式为：

在已知激磁电压U1的条件下，激磁电流I1表达式为：

式中，R1激磁绕组直流阻值，Re等效铁损电阻，σ漏磁系数，Ag等效截面积。记传感器的灵敏度为KP，则U2=KPα，灵敏度的计算公式为：

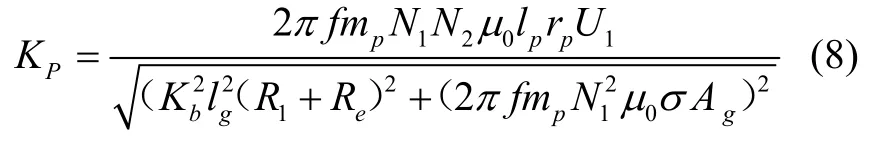
式(6)～式(8)即为动圈式角位移传感器的设计估算模型。在确定激磁电源、结构尺寸、导磁材料及线圈绕组等参数条件下，一般要对传感器的激磁电流、工作气隙磁密、空载灵敏度、磁路饱和程度及空载相位移等电气参数进行计算分析。由于动圈式传感器的工作气隙较大，传统的设计方法难以对传感器交流磁场的分布状况及漏磁通的影响进行准确地分析，对激磁电流、工作气隙磁密等参数无法进行准确计算，即式(9)的函数表达关系f1、f2、f3无法精确地得到，因此其设计误差较大，不适于较高精度的工程设计要求[7,9-10]。

为了实现灵敏度提高30%，激磁电流变化率小于10%，零位电压、非线性度等优于原设计方案这一设计要求，从式(8)可以看出主要的设计参数为线圈匝数N2、激磁电流I1、激磁绕组N1，这些参数之间存在相互交联。例如，增大输出线圈匝数N2可以提高KP，但N2的增大受到动圈窗口面积和输出阻抗不可能太高的限制，需适当调整；增大激磁电流I1，即降低激磁线圈匝数N1，同时KP又与N1成正比，优化目标要求电流I1降低20%。由于参数之间相互交联，无法通过公式得出最佳设计方案，需通过有限元分析方法，结合工艺情况，最终给出最佳设计方案。

2 元件优化设计

2.1 仿真参数确定与建模

通过对动圈式角度传感器进行数学建模与分析，同时为提高仿真效率，确定以下仿真参数，并依据限制条件确定其取值范围：其中激磁绕组N1、气隙长度lg、工作半径rp在其原来值的基础上乘以系数（匝数取整），系数步长为0.05；输出绕组N2的系数步长为0.05，因采取的实现方式不同分别计算[7]。在仿真参数设置的同时还需考虑工艺方法的可行性和继承性，例如增加匝数优先考虑槽满率余量，其次降低线径。传感器几何模型的构建是逐级完成的，首先定义图形参数，其次是点，最后是线，面及体是在面域创建之后自动形成，建模过程对表1 中的仿真对象进行了参数化定义。

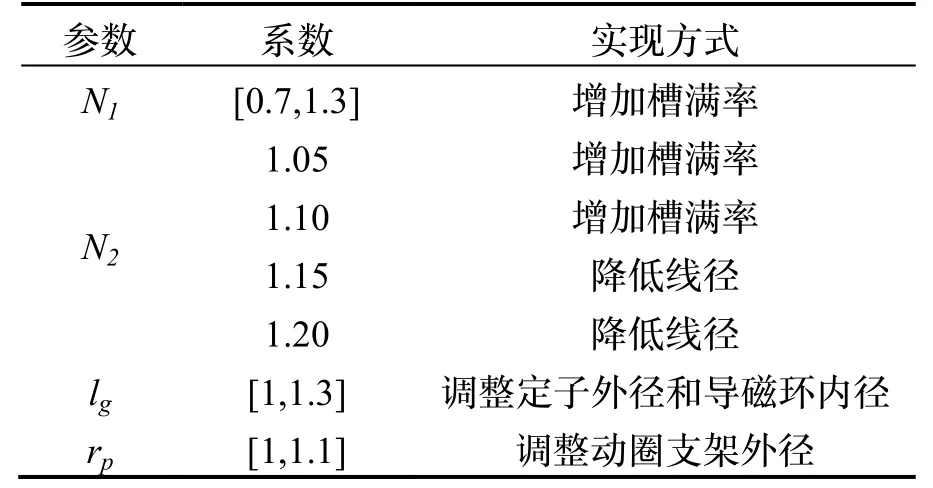
表1 仿真参数设置Tab.1 Simulation parameter setting

参数化途径主要有两种：一种是结构参数化采用坐标点，在结构建模时在Geometric parameter 中完成，实现调整定子外径、外导磁环内径和动圈支架外径；另外一种是电磁属性参数化，在线圈属性中parameter I/O 中完成，实现N1和N2绕组参数、线径的调整。对于模型中的线圈绕组，在建模时采用了简化处理，选择了non meshed coil 线圈形式，提高计算效率。对于传感器中的一些采用非金属材料的结构件，则进行了忽略，合理地简化了模型。所建模型的边界条件采用Infinite Box 设置，软件自动设置边界条件为magnetic field tangent，所建模型如图2。

图2 多极动圈式传感器结构模型Fig.2 Structure model of multi-pole moving coil sensor

由于传感器工作气隙的磁场分布决定了传感器的主要性能和精度，是分析的重点部分，因此相应地增加了与之有关的几何单元的剖分节点，提高工作气隙的剖分精确度。此外，为了减小工作气隙的剖分差异所带来的分析计算误差，对传感器8 个磁极的剖分采用mapped 设置，并应用Linked 使之相互关联，保证磁极及其工作气隙剖分的一致性和对称性，尽量减小由于剖分设置而可能引起的分析计算误差。经检查，模型的剖分质量符合要求。

2.2 求解与数据处理

Flux 提供的求解器与具体的应用模块有关，是个交互的求解过程，由用户控制求解精度和时间步长。根据实际问题分析的需要选择求解模块，在此选择Steady State AC Magnetic 求解模块。参数设置如表1所示，共涉及4 组参数，其中气隙长度lg和等效半径Rg为结构参数、激磁绕组匝数N1和输出绕组匝数N2为电气设置参数，仿真的观测量为传感器输出灵敏度和相位移。

八极式动圈传感器，激磁绕组接线方式为串联反接，瞬态极性为NNSSNNSS 分布，如图3所示。同时通过仿真确定磁路最大磁感应强度为3 mT，出现在内导磁环同一组磁极之间位置。

图3 交流电磁场分布仿真Fig.3 AC electromagnetic field distribution simulation

图4 激磁绕组和输出绕组与灵敏度、相位移关系仿真Fig.4 Simulation results of the relationship between N1,N2 and sensitivity &phase displacement

图4-7 给出了部分参数的仿真结果。结果表明，存在以下规律：（1）灵敏度和相位移随着激磁绕组N1的减小而增大，随着输出N2的增大而增大；（2）灵敏度随转动半径Rg的增大呈现先大后小的规律，且在增加值为0.21 mm 处达到最大，相位移不受Rg的影响。气隙长度lg对灵敏度和相位移的影响较为不规律，气隙长度减小0.84 mm 时出现奇点，奇点原因为输出绕组过于接近磁极，而远离气隙中心点，导致计算误差较大；（3）激磁电流的主要影响因素为激磁绕组N1，随N1减小而增大。

图5 气隙和转动半径与灵敏度、相位移关系仿真Fig.5 Simulation results of the relationship between Rg,lg and sensitivity &phase displacement

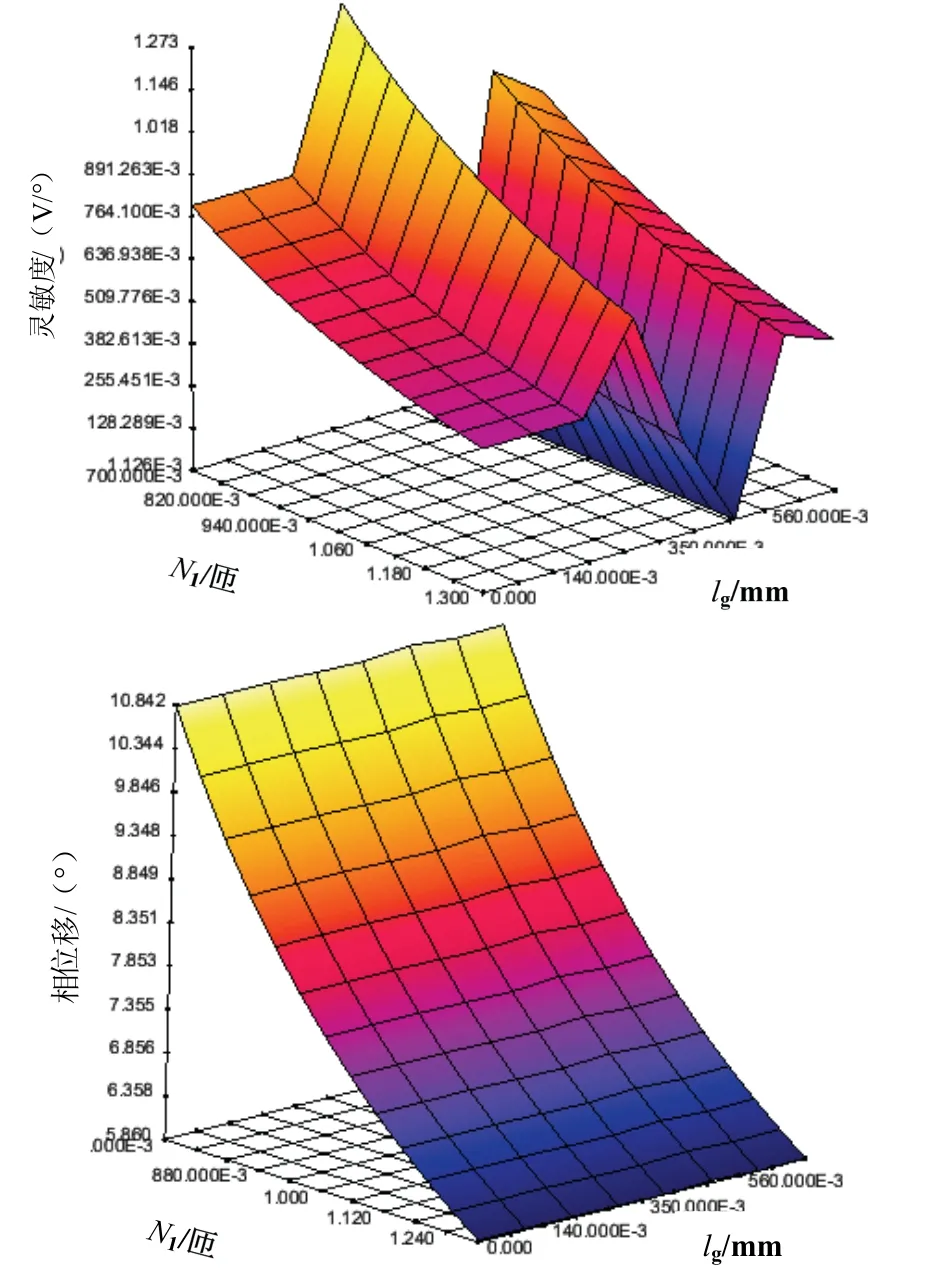
图6 激磁绕组匝数和气隙长度与灵敏度、相位移关系的仿真结果Fig.6 Simulation results of the relationship between N1,lg and sensitivity &phase displacement

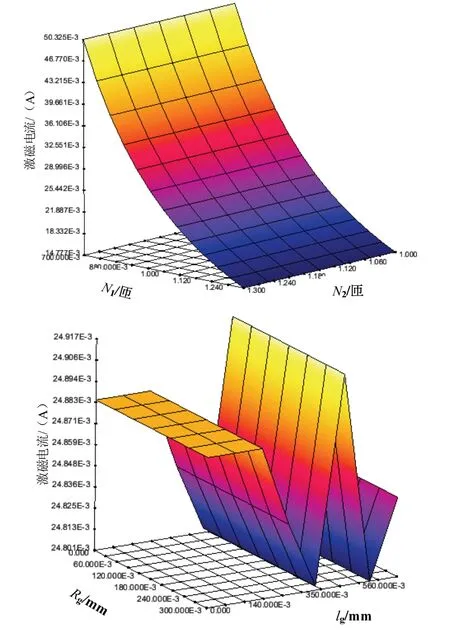
图7 参数与激磁电流I1 影响关系的仿真结果Fig.7 Simulation results of the relationship between the parameters and the excitation current I1

依据灵敏度提高30%，激磁电流变化率小于10%条件确定最优设计方案，以原方案仿真结果为优化目标。首先原方案电流为 25 mA，电流在[27.5 mA,23.5 mA]之内的N1取值为[0.95,1.03]，原方案灵敏度为560 mV/(°)，目标值为728 mV/(°)，N1的最优值为0.95，以此为基础确定lg为0.1 mm、Rg为0.1 mm、N2为1.1，其计算结果为灵敏度752 mV/(°)，激磁电流为27.3 mA，方案对比见表2。

表2 仿真最优设计方案Tab.2 Simulation optimal design scheme

3 实验验证

由于表2 给出的新的设计方案是基于动圈式角度传感器数学建模和有限元仿真分析来的，目的在于满足产品新的指标要求，因此需要从两个方面进行验证：（1）实测数据与仿真数据的符合度验证，即数学模型、有限元模型正确性；（2）实测数据和指标要求的符合度验证，即验证新方案实物是否满足指标要求，设计方案是否有效。

依据有限元仿真给出的新方案，采用相同的工艺方法生产试验件，并完成传感灵敏度、零位电压、相位移、激磁电流、非线性度指标的测试。实验共生产样本13 件，调试结果均满足要求，其中零位电压、相位移、非线性度三项指标包络对比见图8（原方案样本为随机抽取的已交付合格产品，数量13 件）。

从包络分析可以看出，新方案的零位电压、相位移、非线性度满足指标要求，且与原方案保持相接近的包络范围，这主要是因为方案仿真优化时充分考虑了工艺的可行性和继承性。对样本进行统计分析，并将原方案仿真与实测、新方案仿真与实测四者进行对比，结果见表3。

图8 新方案与原方案实测数据对比Fig.8 Comparison of the measured data between the new original scheme and original scheme

从测试结果来看，新方案角度传感器实测灵敏度为731 mV/(°)，提高了35.8%；激磁电流26.1 mA，增大了9.2%；零位电压3.2 mV；非线性度1.8%，即新方案在不改变机械接口尺寸和激磁电源的情况下，实现了灵敏度Kp提高30%，激磁电流I1变化不大于10%，零位电压小于5 mV，非线性度优于5%的设计目标。

表3 仿真与实测数据比对比Tab.3 Comparison of simulation and measured data

从表3 中可以看出新方案实测结果零位电压和相位移方面较原方案要差，零位电压大了0.5 mV，相位移大了0.4 °，这主要是因为新方案降低激磁绕组、增大激磁电流导致元件输入阻抗中的感抗分量减小，元件的品质因数有所下降。

另外，新方案实测结果和仿真结果之间存在一定的误差，实测结果零位电压高了0.7 mV、相位移高了1.9 °、灵敏度低2.8%、激磁电流低了4.4%、非线性度高了0.6 个百分点。这些误差主要是有限元仿真时未考虑材料不均匀性、各绕组的不对性以及测试线路引入的干扰等因素，而这些因素是零位电压、相位移、非线性度的主要误差源。同时，Flux 中的non meshed coil 是一种理想的集中绕组模型，与实际的绕组存在一定的误差，绕组内外孔越接近误差越小。实测结果和仿真结果对比可以看出，仿真误差在可接受范围内，论文所建的数学模型和有限元仿真模型是正确的，有一定的工程意义。

4 结论

高精度浮子角度感知是三浮陀螺仪实现高精度目标的重要技术路径，在方案升级中要求在不改变角度传感器机械接口尺寸的前提下提高灵敏度，且激磁电流、零位电压、相位移控制在一定的合理范围。由于传统电磁计算方法在动圈式角度传感器计算中存在较大误差，设计验证周期较长。本文从变压器磁链方程出发，推导建立了适合于动圈式角度传感器的灵敏度、激磁电流数学模型，结合设计目标对模型进行分析，确定了激磁绕组、输出绕组、气隙长度和转动半径为设计切入点，采用有限元仿真技术，建立参数化模型，通过仿真给出新的设计方案。实验数据表明新的设计方案使角度传感器灵敏度提高了35.8%，激磁电流变化控制在9.1%，零位电压3.2 mV，非线性度1.8%，实现了灵敏度Kp提高30%，激磁电流I1变化不大于10%，零位电压小于5 mV，非线性度优于5%的设计目标。同时仿真数据与实验结果在可接受误差范围内，证明论文提出的基于有限元分析方法的三浮陀螺用角度传感器优化设计方法有效。