基于数字孪生的飞机机体曲面重建与偏差分析*

王 巍，门 宇

（沈阳航空航天大学航空宇航学院，沈阳 110136）

飞机是一个庞大而复杂的产品，大量的零件相互作用，相互配合，研制过程中由于零件的制造误差与部件的装配误差以及各种不确定因素的存在，零件间会出现干涉而无法装配等问题，需要对原有设计进行反复修改，直至装配成功，经常导致产品研发超出规定时间。实际生产中物理空间真实产品与虚拟空间设计产品状态不一致的问题，在数字孪生技术出现后得到了有效改善[1]。数字孪生技术是将物体数据从物理空间返回到虚拟空间的设计过程，通过激光扫描或传感器等精密数据采集技术提取物体表面关键特征数据，实现快速模型重建，将物理空间的实体映射到虚拟空间，并在虚拟空间进行多尺度、多概率的仿真分析，达到实际生产零失误的目的，保证生产快速平稳进行[2]。数字孪生技术实现了产品制造信息的反馈，准确描述模型，推理分析，优化生产，推动智能制造更进一步发展。董雷霆等[3]研究的数字孪生技术应用于飞机结构建模仿真，能够通过传感器进行在线监测，实时获取飞机运行中的各项源数据，反映并预测飞机结构实体在全寿命周期内的行为和性能。刘勇等[4]将数字孪生技术应用于模具修复中，实现了模型快速重构与偏差分析，最大程度地降低模具的更换与维修成本。此外，数字孪生技术也可为无模型支撑的实体建立孪生模型，实现文件的永久留存，为产品的再次设计与开发提供真实的理论依据，具有重要意义。

1 实体数据采集与处理

1.1 数据采集

模型和数据是决定数字孪生系统能否高效运行的基础，数据获取的精度是孪生系统能否精确指导生产的关键。随着技术的发展，数据采集的精度不断提高，但孪生模型永远不可能完全准确地感知物理实体，只会无限接近实体[5]。数据的获取选择关节臂激光扫描测头进行采集，设备便携，操作简单，在大量物体表面数据的快速采集方面占据绝对优势。激光亮度高、单色性好、抗感染性强的特点使其被广泛应用于物体在线检测中，如在焊接领域可以用来提取焊接表面特征，识别缺陷[6]。在扫描时，对于不能一次完成扫描的模型，在每一次扫描中，需要扫描一定量的具有明显特征的共同部分，也可在被扫描模型周围放置一定数量的拼接球，方便点云数据拼接。

点云的质量除了受操作者操作方法影响外，还受周围环境（如光线、噪音等）影响，难免会出现一些噪点，在被测物体周围也会因超出测量范围而出现零值，或因激光束照射在物体上的反射光线产生干扰数据。首先删除点云数据中的由于各种干扰而产生的噪点；其次，删除漂浮在物体外的数量较大的杂点。对于多个不同站位扫描的点云，需要手动进行两两拼接，采用“n点对齐”模式进行对齐[7]，应用拼接球的也可通过“探测球体”的方式进行对齐，再进行全局注册，最终得到更高质量的完整拼接点云数据。激光扫描点云数据密集，数量庞大，短时间内可达到上千万个点，大量的点是孪生模型重建时所不必要的点，这些点会增加软件的运行负担，需根据实际需要对整体点云进行统一采样，具体流程见图1。

1.2 点云数据网格化与坐标系对齐

网格化时采用3D网格，网格面是由临近的3个点所构成的三角平面所组成，设置合适的临近值参数，保证网格不出现畸变前提下漏洞最少。

在进行孪生模型重建之前，将点云数据对齐到世界坐标系可在一定程度上使建模更加便利。无论是正向建模还是逆向建模，坐标系都是辅助建模最有效的参照基准，合理的选取坐标系会为后续建模带来便利。扫描时点云数据的点位坐标是相对于获取点云的设备坐标系的，因此需要在飞机模型所对应的网格面上正确选取坐标原点及坐标平面，建立一个基准坐标系，应用定位变换功能将网格模型对齐到绝对坐标系。坐标系的建立应遵循保证飞机的外形特征与其有尽可能多且简单的相对关系的原则。

1.3 基于特征的点云数据区域划分

要想得到更加接近实体的数学模型，首先要对物体结构进行分析，对不同的结构采取不同的重建方法，保证重建模型与原有模型能够最大程度地契合。在飞机制造生产过程中，零件模型的结构除了平面、圆柱面、锥面、球面等基础的简单形面外，更多的是复杂的不规则几何曲面，大体可分为条状类、回转类和平缓类三种曲面形状[8]。条状类曲面与回转类曲面特征曲线可通过相对应的平面截取网格面获得。领域划分线即为不同结构间的分界线，这类曲线需要对网格面的曲率进行分析，在曲面分形附近获取等曲率曲线。

2 基于数字孪生的曲面重建方法与检测

2.1 基于数字孪生的曲面重建方法

孪生模型重建是零件数学模型反求过程中最为复杂也是最关键的部分，是将产品信息数字化，进行再设计与再生产的基础[9]。规则的几何形状可通过软件相应的拟合操作或通过切面绘制草图的方式进行模型重建。复杂曲面的特征曲线的拟合是曲面重建的关键，关键步骤如图2所示。

在进行曲线拟合时，为避免特征曲线位于曲面与曲面间的倒角内侧，影响曲线曲率，将上文所提到的形面分界处的曲线拟合成3D曲线后，向远离倒角一侧平移1～2mm的距离（若有明确参考方向也可直接将3D曲线平移），将平移后曲线投影至网格面上再一次拟合。

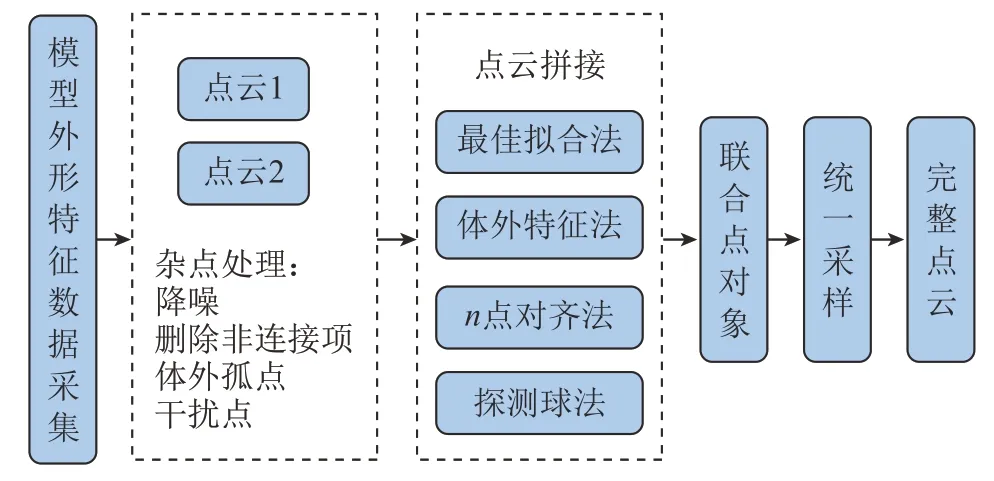
图1 数据采集与处理流程Fig.1 Data collection and processing flow

图2 复杂曲面重建流程Fig.2 Complex surface reconstruction process

特征曲线的拟合精度将直接影响曲面的精度，在将投影曲线转换为3D曲线时，若拟合的曲线曲率变化或偏差过大，可将该曲线在合适的位置断开，断开后曲线曲率变化和偏差会有明显改善，直至曲线偏差在允许范围内。检查断开处曲线的连续性，保证曲线首位相连。

曲面拟合的精度即为孪生模型重建的精度。条状类曲面与回转类曲线均可通过拟合好的截面曲线与引导线建立多截面曲面；平缓类曲面需要按一定距离截取两组网格曲线，截取平面相互垂直或根据曲面边界自定义，将所有曲线拟合成曲线网格，再通过曲线网格进行曲面拟合。

由于每个曲面都是单独拟合的，曲面与曲面间曲率不连续，甚至有较小间隙。用等参数曲线功能可在曲面边界附近截取曲面上的曲线，在需要光顺连接的曲面连接处附近分别作出曲线，用所作出的曲线裁剪曲面，保留远离交线一侧的曲面，再用桥接曲面功能将曲面顺接。桥接的两个曲面间隙不宜太大，边界曲线应尽量保证长度相同，对于封闭曲线应保证闭合点位置合适且方向相同，避免桥接曲面发生扭曲。当所有曲面拟合完成，将其结合在一起，即可得到一个完整的光顺曲面。

为提升拟合精度，曲线拟合结合了NURBS法[10]。定义中，每一条NURBS曲线都可以用有理多项式来表达，指定一条线路，在多个点之间以插值的形式进行替换，最终得到一条光滑曲线。其定义如下：

式中，Bi为第i个控制点，Ni,k（u）为样条基函数，定义如下：

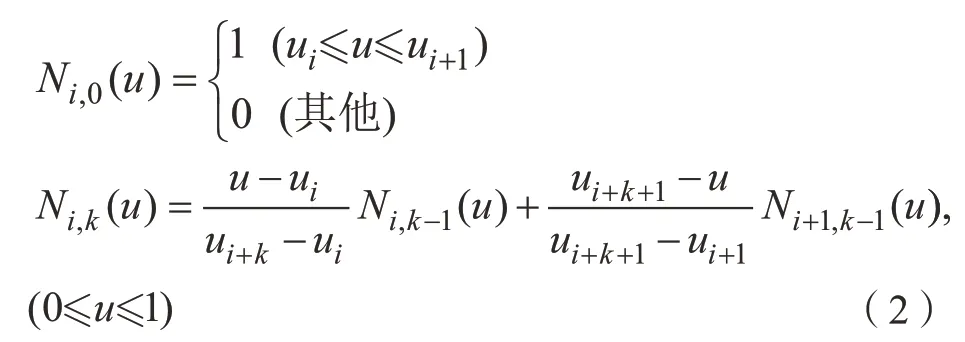
则k阶B样条曲线的数学表达式为：

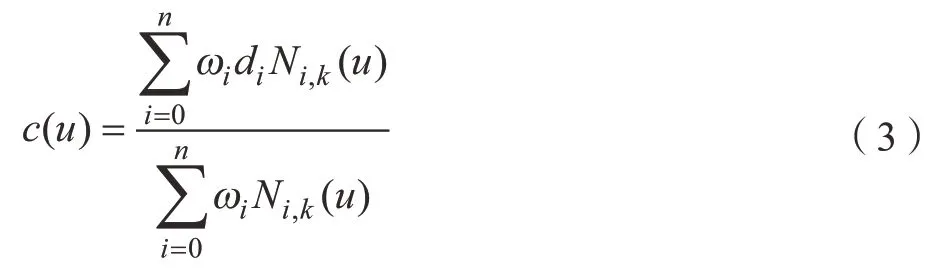
式中，ωi为权因子，di为控制定点。

在曲线拟合参数设置中，由于NURBS曲线为立方等式，次数为3，即阶数为4，增加阶数可使曲线更加圆滑，但也会使计算量成倍增加，故不建议使用更高阶数的曲线；曲线一阶连续，参数设为1；容差设置为0.01，虽然偏差会超过设定值，但能最大程度地控制曲线精度。

曲面拟合是在曲线拟合基础上的扩展，其数学定义为：

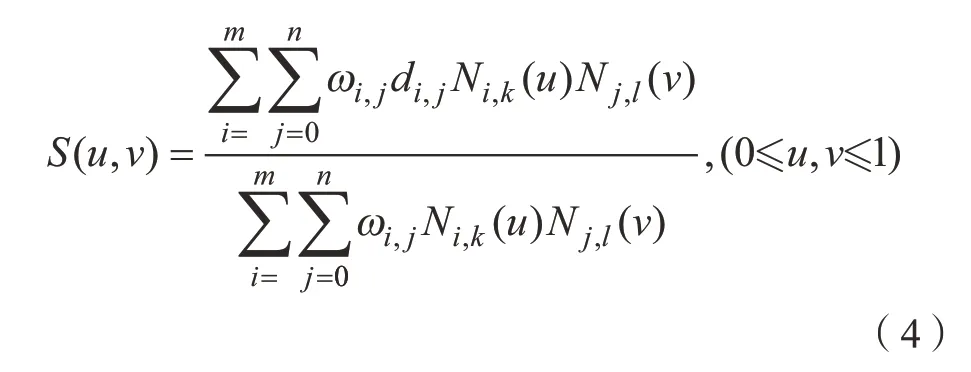
式中，ωi,j为权因子，di,j为控制定点；Nj,l(v)为v方向的样条基函数。

为保证曲面质量，在相框处光顺连接，将参数连续性设为C1曲率连续，几何连续性设为G2连续。

2.2 孪生模型的检测

3D比较是自动化检测的主要方式之一，通过孪生数字点云构建曲面模型并控制拟合精度，对产品真实的外形尺寸、曲面曲率等进行分析，达到检测孪生模型质量的目的。在实际生产中也可将孪生的真实模型与产品理论设计模型在同一个三维空间进行整体比较，分析其制造误差，将带有误差的孪生模型在虚拟空间进行装配仿真，检验其制造误差对产品过程的影响，如在装配过程中是否会出现干涉导致无法装配或因接触不严而无法连接的现象；是否会产生较大的装配应力从而影响产品的使用寿命等，提前发现问题并给出合理的解决方案，如图3所示。由于是在线虚拟自动检测，3D比较的效率高，且人为参与较少，多为人机交互界面的自动化操控，人为误差降低，提升了检测精度，检测结果参考价值高，为产品制造过程提供一定的指引。因此，本文应用3D比较方法，基于孪生模型对产品进行检测。

3 实例应用

以某型低音速飞机为例，飞机头部为发动机舱，外有圆形发动机罩，曲面类型为回转类曲面；机身侧面为拉长的流线形，其剖面为方形，其形面为典型的条状类曲面；机翼、平尾和垂尾的上、下或左右翼面为平缓类曲面，前缘与后缘部分需划分为条状类曲面。飞机各组件外表光滑且曲面间曲率连续，可将飞机孪生模型的建立分为机头（发动机罩）、机身、翼面（机翼、平尾、垂尾）、曲面过渡等4部分进行建模。

首先建立机体坐标系，将飞机航向设为X轴，翼展方向设为Y轴，飞机停止时，垂尾与地面垂直设为Z轴。通过观察飞机模型，飞机机翼和方向舵有明确的特征能够帮助建立坐标系，通过翼展方向和方向舵垂直方向来确定飞机航向。翼展方向轴线可通过左、右襟翼或升降舵与机翼连接部分的顶点来确定，为提高准确度，选择距离最远且明显的特征建立Y轴轴线；建立的直线取中点为原点并建立法线平面为XZ平面；在XZ平面内通过方向舵与垂尾连接位置确定Z轴方向和X轴方向。最终将网格模型对齐到绝对坐标系（图4）。

通过分析飞机模型网格面曲率，获得机翼、平尾、垂尾与机身间的分界线；机头的特征曲线为YZ面截图的轮廓曲线和YZ及其旋转平面截取的引导线，机身的特征曲线为YZ面截取的轮廓曲线和曲率分析时所得到的航向机身曲线。对拟合的曲面进行偏差分析与曲面质量评估，调整偏差较大部分的曲线拟合参数，直至合格（图5）。

经大量数据分析发现，不同类型曲面的拟合精度有一定差异，平缓类曲面拟合精度相对较高，各个方向曲率均变化平缓，回转类曲面次之，条状类曲面由于其横向截面变化幅度较大，曲线拟合时易出现较大偏差，曲率变化明显，但绝大部分曲面精度能控制在0.05mm以内（表1）。

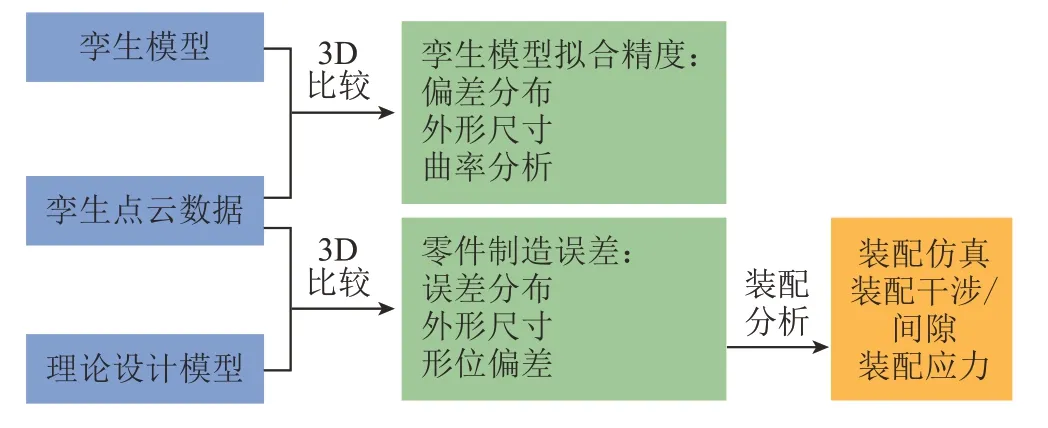
图3 3D比较Fig.3 3D compare

4 结论

复杂曲面孪生模型重建的重点难点在于能否准确提取其特征曲线并进行更高质量的拟合，保证重建曲面的精度。本文提供了一种能够多层次控制曲面精度的拟合方法，由确保特征曲线的精度来控制曲面的精度，由局部到整体，层层把控，有利于及时发现产生较大偏差的原因以及所在位置，并及时修正，有效控制孪生模型整体偏差，适用于曲率变化平缓、尺寸较大曲面如机身机翼等表面质量的快速检测。未来需要将数字孪生技术更多地应用于飞机制造的检测中，以提升飞机检测的自动化程度，提高检测效率和精度。

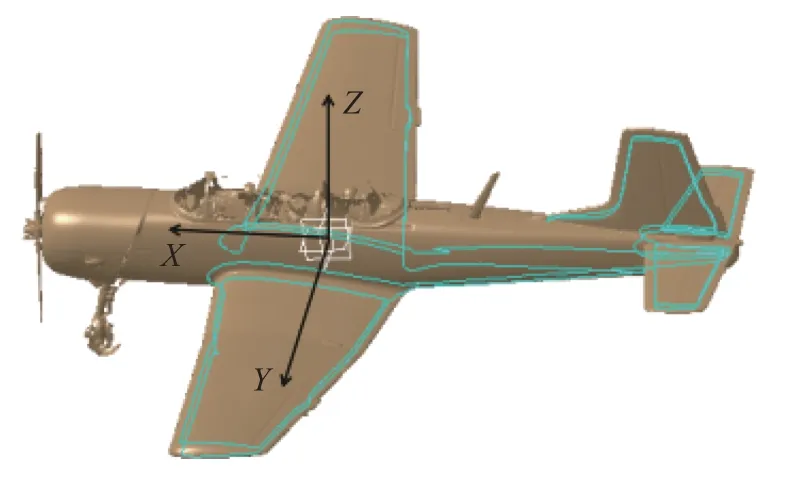
图4 坐标系建立Fig.4 Coordinate system establishment

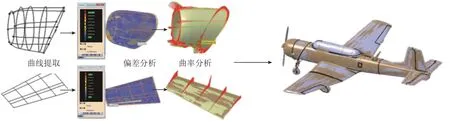
图5 孪生曲面重建与质量评估Fig.5 Reconstruction and quality evaluation of twin surfaces

表1 不同类曲面质量差异Table 1 Quality difference of different kinds of surfaces