基于机器学习的毫米波MIMO系统波束成形设计

频率在30～300 GHz的毫米波通信因为具有极大的带宽优势，成为目前无线通信领域的研究热点之一.毫米波通信系统可搭配大规模多输入多输出(multiple input multiple output, MIMO)技术，通过使用成百上千的天线显著提升系统的频谱效率和能效[1].其中，大规模MIMO系统以波束成形技术获得的高增益克服毫米波通信系统的高路径损耗问题.

基于小规模MIMO系统开发的传统波束成形方案在大规模MIMO系统中将面临高成本、高功耗的问题.该问题的一种解决方案是使用混合结构的波束成形系统.混合结构波束成形系统包含低维度的数字预编码器和高维度的模拟预编码器，通过使用数量远少于天线数的射频链来实现成本和功耗的有效降低[2-3].在实际应用中，模拟预编码器一般由有限精度的相移器组成，其恒模约束导致混合波束成形的最优化设计问题难以直接解决.通常采用基于码本的搜索方法来设计模拟预编码器.理论上最佳的模拟预编码器可通过穷尽搜索法(exhaustive search algorithm, ESA)来得到，但因其搜索复杂度与相移器的量化位数和射频链数呈指数关系，无法在实际中应用.

在模拟预编码器的设计问题上，目前已有一些基于码本的低复杂度搜索的研究.例如，Wang等提出一种基于多分辨率码本的低复杂度方案，以自适应方式细化模拟波束形成矢量[4].Hur等则采用乒乓抽样策略结合多级码本来降低搜索复杂度[5].文[6]使用类似Turbo策略的波束成形方案以减少搜索复杂性.文[7]提出了交叉熵最优化(cross-entropy optimization,CEO)搜索方法，能够以远低于ESA的搜索复杂度获得不低于98%的最佳数据可达率.但是文[7]中的传统CEO算法没有充分利用已知的信道状态信息(channel state information, CSI)，并且在概率更新时没有考虑数据可达率的大小，收敛速度还有待提高.在文[7]的基础上，本文提出两种改进的自适应CEO算法，通过非均匀的初始化概率分配策略和与数据可达率相关的概率更新策略有效提升CEO算法的收敛速度.

1 毫米波大规模MIMO系统模型

点对点毫米波大规模MIMO下行传输系统如图1所示.基站和移动端都采用混合预编码结构，其中基站的天线数和射频链路数分别为Nt和Mt，移动端的天线数和射频链路数分别为Nr和Mr，系统支持同时传输D路数据.受到功耗和成本约束，一般移动端天线数远少于基站天线数，基站和移动端的天线数、射频链路数和数据流数量满足D≤Mt≤Nt和D≤Mr≤Nr.

图1 点对点毫米波大规模MIMO通信系统模型Fig.1 Point to point mmWave massive MIMO system

在发射端，数据流s∈D×1依次经过数字预编码器G∈Mt×D和模拟预编码器F∈Nt×Mt处理后进入信道.发射信号可表示为

x=FGs.

(1)

(2)

(3)

其中：ρ为发射功率，H∈Nr×Nt表示信道矩阵，n∈Nr×1为加性高斯白噪声，其元素满足复高斯分布CN(0,σ2).

为了表征毫米波信道的低秩特性，采用Saleh-Valenzuela信道模型[7-8]，其信道矩阵可以表示为

(4)

其中：Lc是散射簇的数量，每个簇包含Lp个传输路径.βc,p～CN(0,1)表示第c个散射簇中第p个路径的复增益，θc,p和φc,p则分别是该路径的发射方位角和到达方位角.gt(θ)与gr(φ)分别表示发射端和接收端天线阵列响应向量，当采用均匀线性阵列时，天线阵列响应向量可表示为

(5)

其中：λ为电磁波波长，d是相邻天线单元的间隔，N为天线单元的数量，θ表示天线阵列的发射角或到达角，(·)T表示矩阵的转置.

令M∈Mr×D和W∈Nr×Mr分别表示接收端的数字组合器和模拟组合器，经过信号处理后的估测信号可以表示为

(6)

对于毫米波大规模MIMO系统，在发射端获得CSI对预编码器设计至关重要，该信息可以通过文[9-10]所提方法来获得.和文[6-7]类似，本文假设发射端和接收端均已获得准确的CSI，聚焦于发射端模拟预编码器和接收端模拟组合器的联合最优化设计，但不包括基带数字预编码器的设计.

2 模拟波束成形

2.1 码本设计

实际模拟预编码器由有限精度的相移器组成，常用设计方法是基于码本的波束成形方案，即预编码器由预先设计好的码本中的导向向量组成.我们选择离散傅里叶变换(discrete Fourier transform, DFT)码本作为模拟波束成形码本，因为DFT码本具有以下特点：①不同向量之间是无关的；②全部向量的线性组合可以合成任意导向向量集张成的向量空间.传统的M维DFT矩阵的第k列可表示为

(7)

其中：AM(:,k)表示矩阵AM的第k个列向量.比较式(7)和(5)，不失一般性，当M为偶数时可得到如下关系:

(8)

式(8)表明，DFT矩阵与一组对方向角正弦值均匀采样的导向向量集合对应.令式(7)的M分别取值Nt和Nr，可分别得到发射端和接收端的模拟波束成形码本F{ANt(:,1),…,ANt(:,Nt)}和W{ANr(:,1),…,ANr(:,Nr)}.

2.2 模拟预编码器设计问题

从发射端码本F提取Mt个向量即可得到模拟预编码器F.同理，模拟组合器W由接收端码本W的Mr个向量组成.当给定F和W，基站射频端到移动射频端之间的数据可达率[6-7]可以表示为

(9)

其中：Rz=σ2WHW为噪声相关矩阵，|·|表示矩阵的行列式.本文联合设计{F,W}使得数据可达率R(F,W)最大化：

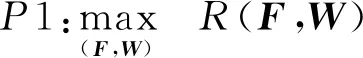
(10)

W(:,j)∈W,1≤j≤Mr.

注意到式(10)中F(:,i),1≤i≤Mt和W(:,j),1≤j≤Mr都可以由相应的量化相位确定.设发射端码本F对应的相位集为Θ={θ1,…,θNt}，接收端码本W对应的相位集为={φ1,…,φNr}.F和W可以进一步表示为

(11)

(12)

3 自适应加权CEO算法

3.1 传统CEO算法

CEO算法的核心是参数化概率分布的迭代调整，逐步提升获得最佳解的概率.问题(12)中，首先要建立用于生成候选解ω{a,b}的参数化概率分布.发射端产生一个随机样本a的简单方法是从Θ中独立的抽取假设服从Nt点离散概率分布{p1n,…,pNtn}，其中pμn,1≤μ≤Nt,1≤n≤Mt表示集合Θ中第μ个量化相位被选中为的概率，即事件发生的概率.通过概率矩阵P{pμn}∈Nt×Mt，可得到为每个相移器分配量化相位的方法.发射端的参数化概率分布记为

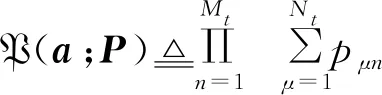
(13)

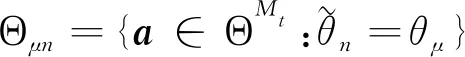
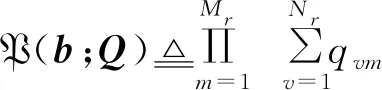
(14)

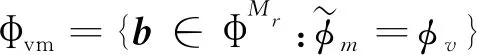
P(ω;Λ)P(a;P)×P(b;Q).

(15)

传统CEO算法解决问题(12)包含以下步骤[7]：

①以均匀分布的方式初始化概率矩阵Λ.

②基于给定的概率分布，随机产生K组候选解，计算每组解的数据可达率.对数据可达率降序排列后，选取前KE个解做为精英解.

③以均匀分布方式对精英解重新分配概率.

④通过平滑操作对概率矩阵进行更新.

⑤重复步骤②③④，当算法收敛时将以足够高的概率得到最佳解.

传统CEO算法可以获得非常接近ESA算法的最佳解[7]，但还存在一些不足.首先，步骤①的均匀概率分布策略没有充分利用已知的CSI.利用CSI，可以预先判断哪些发射角和接收角更有利于信号的传输.通过特定机制对码本中量化相位进行非均匀概率初始化，可以在一开始就得到“较好”的解，从而提升CEO算法的收敛速度.其次，步骤③中，传统CEO算法使用均匀分布策略对精英解重新分配概率，忽略了数据可达率大小的信息.直观来讲，更高的数据可达率对应的解应该赋予更大的概率.此外在步骤②中，精英解仅从当前K个样本中产生，未综合考虑历史迭代过程中的精英解信息，前后迭代的弱相关性会造成在CEO算法迭代过程中性能的波动.为了克服以上传统CEO算法的不足，我们提出了自适应加权CEO算法来提高算法的收敛速度.

3.2 自适应加权CEO算法

先对信道矩阵进行分析并建立相位与概率大小的关系.基于发射端码本ANt、接收端码本ANr和信道矩阵H，定义角度域的信道矩阵Ha为

(16)

注意到发射端天线阵列在ANt波束成形作用下，将产生Nt个中心角位于{θ1,…,θNt}的波束图.接收端天线阵列在ANr波束成形作用下，将产生Nr个中心角位于{φ1,…,φNr}的波束图.式(16)可以解读如下：角度域信道矩阵Ha∈Nr×Nt的第(i,j)个元素的模表示当发射端使用第j个导向向量，同时接收端使用第i个导向向量进行波束成形时的信道增益.图2为Nr×Nt=16×64天线阵列的毫米波信道角度域增益的示意图.

显然，与大的角度域信道增益值所对应的波束成形向量更有利于信号传输，反之亦然.基于以上分析，我们提出根据角度域信道增益的大小，对码本中不同的导向向量赋予不同的初始概率，提升CEO算法的收敛速度.具体方案如下：

①根据式(16)计算角度域信道矩阵Ha.

②记录每个发射端波束所对应的最大角度域信道增益(接收端遍历全部波束)于向量t：

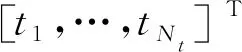
(17)

其中：|·|∞表示最大模.

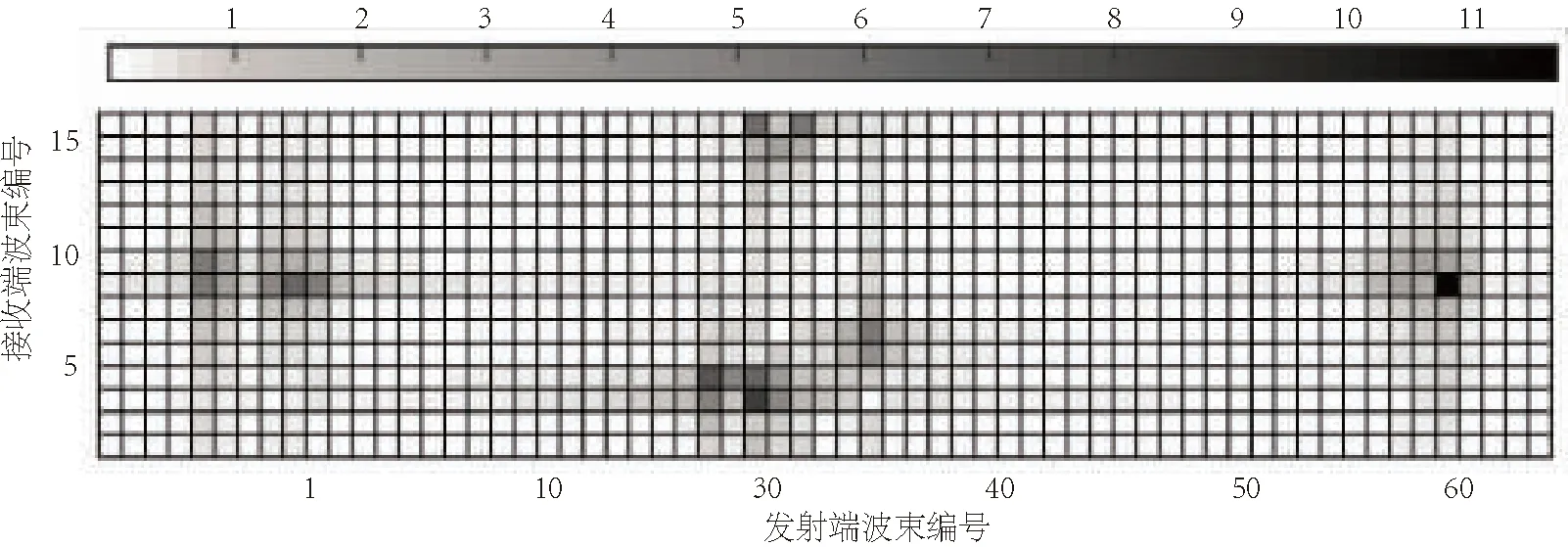
图2 角度域信道增益示意图Fig.2 Illustration of angular domain channel gain

③记录每个接收端波束所对应的最大角度域信道增益(发射端遍历全部波束)于向量r：

(18)

④计算发射端码本向量的初始概率矩阵P(0)和接收端码本向量的初始概率矩阵Q(0)：

(19)

(20)

另一方面，3.1节中传统CEO算法的步骤③中，精英样本仅从本次迭代的随机样本中产生，并分配均匀化的概率.这样既忽略了精英样本数据可达率大小的信息，也没有充分利用历史迭代的精英样本信息.不同精英样本所对应的数据可达率有大小区别，更大的数据率可达率应分配更高的概率.为了充分利用全部随机试验的信息，我们提出一个全局精英样本概念：将本次迭代产生的样本和前面全部历史迭代产生的样本汇总后降序排序，按比例提取前面几个对应数据率最大的样本作为全局精英样本.每个全局精英样本的概率与其数据可达率的大小成比例关系，即根据数据可达率进行加权.全局精英样本策略可以改善由随机性造成CEO算法在迭代过程中性能波动问题.我们提出的自适应加权CEO算法包含了非均匀初始化概率以及基于数据率大小的全局精英解概率更新方案，其算法流程归纳于自适应加权CEO算法:

④更新概率矩阵P(i)和Q(i)

(21)

(22)

⑤平滑概率矩阵[7]

(23)

其中：0<α<1是平滑常数.

■ 输出最佳解(a*,b*).

3.3 复杂度分析

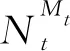
4 模拟仿真

考虑线性阵列尺寸为Nt×Nr=64×16的毫米波MIMO系统，天线单元间隔为半波长.发射端和接收端的射频链路和传输的数据流为Mr=Mt=D=2.SV信道模型参数设置如下：散射簇的数量Lc=5，每个簇包含的传输路径数Lp=10，角度扩展为10度，每个簇的中心角在[0,2π]均匀分布，簇内路径的角度服从截断拉普拉斯分布.发射端和接收端均使用DFT码本.信噪比为0 dB.所有模拟结果均为5 000次蒙特卡罗试验的平均.

首先，研究不同样本数K下两种CEO算法的收敛性能.图3显示了两种CEO算法的数据可达率随迭代次数的变化关系，图中标注“CEO”和“ACEO”分别表示传统CEO算法和我们所提的自适应加权CEO算法.一般而言，样本数K代表了CEO算法在每次迭代时对解空间的搜索能力，过小的K，会容易让CEO算法收敛到局部最佳解，如传统CEO算法中K=200和K=400的情况.只有足够大的K，才能保证CEO算法收敛到全局最佳解，如传统CEO算法中K=1 000和K=1 200的情况.但是对于我们所提出的自适应加权CEO算法而言，由于事先对信道分析得到不同量化相位对应的波束成形向量与信道的匹配情况，通过初始概率矩阵的仔细设计，可以一开始从“好”的候选解继续迭代搜索，在样本数很小的情况下，也可以很快收敛到全局最佳解，如自适应加权CEO算法中K=200和K=300的情况.

为了比较所提算法在计算复杂度上的优势，图4给出了两种CEO算法的性能与计算量的关系曲线，其中横坐标为计算式(9)数据可达率的次数.从图中可以看出，传统CEO算法收敛到最佳解所需累计样本实现次数约为5×104，自适应加权CEO算法达到相同性能所需累计样本实现次数仅为5×103.这说明在解决毫米波MIMO系统的混合预编器设计问题上，我们所提自适应加权CEO算法相较于传统CEO算法有极大的计算复杂度的优势.

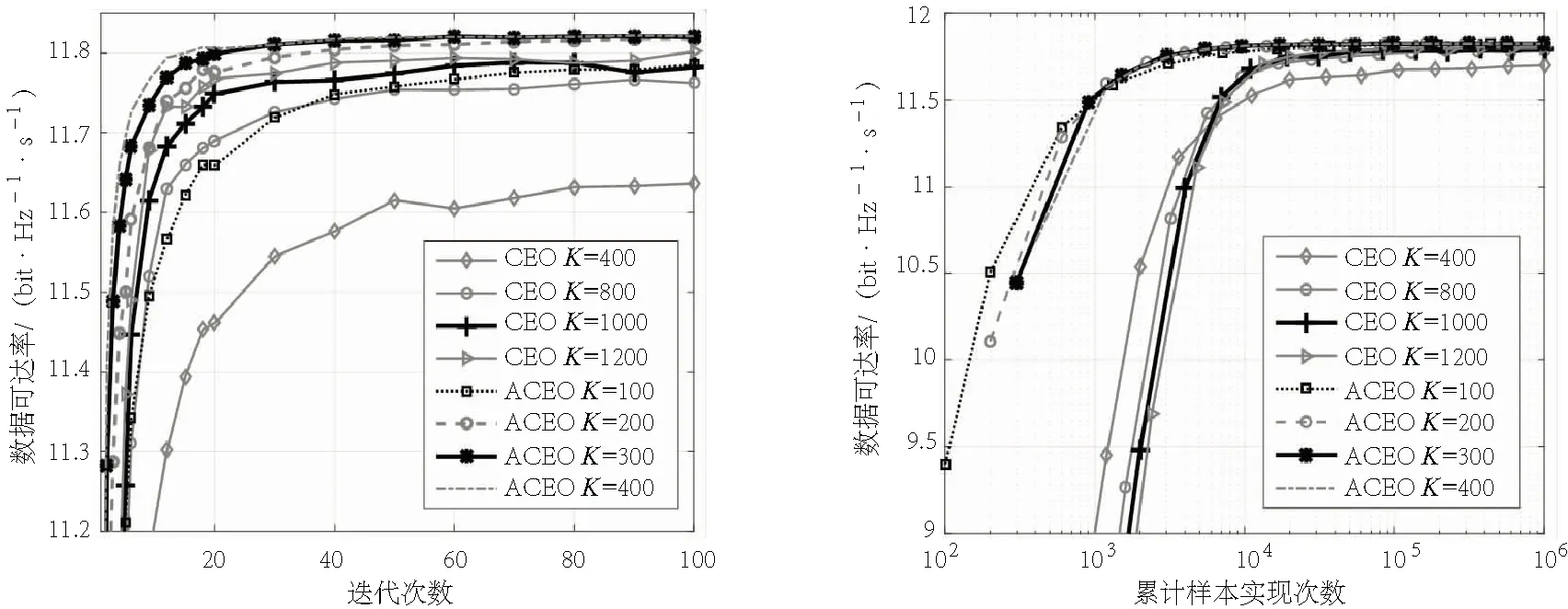
图3 不同样本数K下两种CEO算法的性能 图4 两种CEO算法的计算复杂度比较Fig.3 Effect of the sample size K on Fig.4 Comparison of the complexities two CEO algorithms of two CEO algorithms

5 结论

混合波束成形技术通过减少射频链的数量，被认为是促进毫米波大规模MIMO系统的实际部署的一种经济有效的替代方法.本研究的重点是基于码本的联合模拟波束成形最优化设计.为了解决传统方法过高复杂度的问题，我们提出了一种基于自适应交叉熵最优化的混合预编码方案.仿真结果表明，该算法在较低的复杂度下可获得接近最优的性能.