均布载荷作用下胶接悬臂梁的静态响应分析

史文谱,王 浩,闫家正

(烟台大学机电汽车工程学院,山东 烟台 264005)

层合梁比单层梁有诸多好处,比如刚度强化、受力稳定、力学性能优化、降低应力集中和减少不必要的附重等[1],因而广泛应用于路桥工程、吊装码头、微纳米机电系统[2]等许多场合。在材料力学教程[3]中,对界面不滑移理想结合组合梁问题已有讨论;在假设叠合梁间光滑接触情形下,谢丽君[4]讨论了简支叠合梁的挠度计算问题;谈至明[5]则利用Goodman假设研究了Winkler弹性地基上双层叠合梁的计算问题,给出了解析解;赵亮等[6]利用广义哈密顿原理、有限元法和Newmark迭代法研究了双层叠合梁上存在移动质量时的振动特性问题;揭敏在文献[7]中讨论了密实非胶接自由接触梁的计算问题;唐晓雯等[8]基于层合梁弯曲的Timoshenko理论和电测技术研究和测试了均布载荷作用下的简支(双金属)层合梁的弯曲正应力;罗威等[9]分析了胶接接头可靠性的影响因素和研究进展;陈征辉等[10]分析了胶层厚度、胶接真空度和胶接夹持距离等因素对交接强度的影响问题;罗威等[11]利用ANSYS软件探讨了胶粘剂弹性模量对胶接接头的应力分布的影响。纵观列出和未列出的参考文献看,有关胶接[1]悬臂梁在均布载荷作用下的变形计算和剪切应力分析的问题还未见有论文发表,对此,本文基于线弹性变形和材料力学假设进行了理论研究,给出了胶接梁的挠度、上下梁的轴向位移以及胶层内剪切应力随不同E2/E1时的变化情况,数值算例结果表明胶层内最大剪切应力靠近梁的固定端一侧,且梁的挠度大小和轴向位移大小以及胶层剪切应力大小的变化曲线都随E2/E1的增大呈下降趋势。

1 问题模型和分析

图1是胶接组合悬臂梁,分上梁、胶层和下梁三部分,梁长为L,梁的宽度为b,胶层厚度为δ,上下梁高度分为h1,h2;杨氏模量分别为E1,E2;胶层剪切模量为G。梁的左端固定,右端自由,下梁承受向上的均布载荷作用,线密度为q,建立图示3个坐标系oxw、o1z1y和o2z2y;o1、o2分别是上下梁截面的形心点。假设梁变形和胶层剪切变形是线弹性的,上下梁变形的平面假设成立。

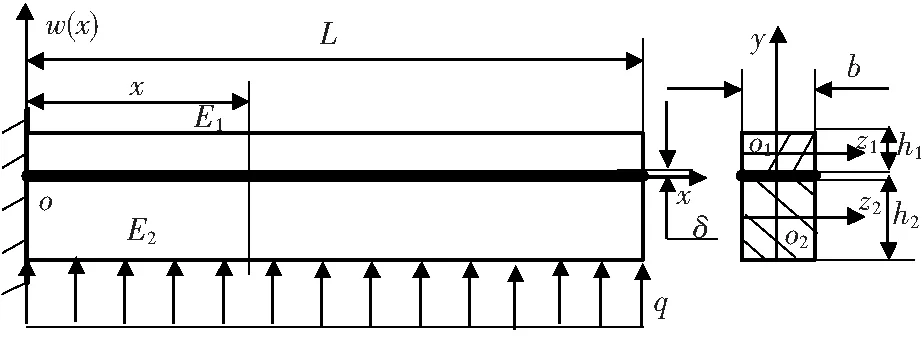
图1 纯弯矩作用下的胶接组合悬臂梁

假设上下梁截面形心线挠度分别为w1(x),w2(x),形心线上点的轴向位移分别为u10(x,y),u20(x,y);上下梁截面上任意点的轴向位移分别为u1(x,y),u2(x,y)。由于胶合梁的上下梁在变形过程中始终没有分离,故根据材料力学知,在小变形假设下,上下梁在同一截面上各点的挠度是一样的,并统一假设为w(x),即

w1(x)=w2(x)=w(x),

(1)

由梁变形的平面假设知,胶合梁任意截面x处上梁截面y1处和下梁截面y2处点的轴向位移u1,u2可分别表示为

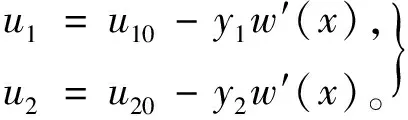
(2)

其中:w′(x)表示挠度w(x)关于x的一阶导数;y1,y2分别是上下梁截面上计算位移的点离其中性轴的距离。

与位移u1,u2分别对应的线应变ε1,ε2可写为

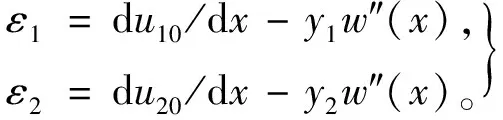
(3)

其中,w″(x)是挠度w(x)对x的二阶导数。

胶层很薄,其角变形假设为线弹性的,从几何关系上,其剪切应变γ为

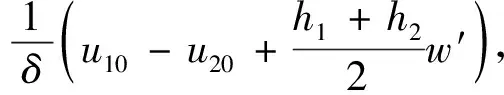
(4)

由问题的本构方程(胡克定律)有

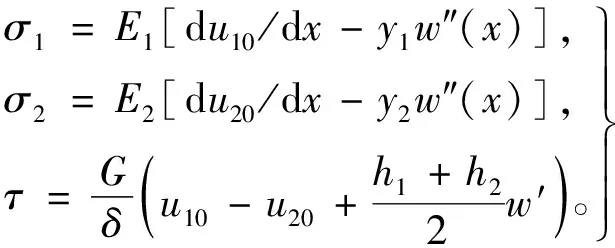
(5)

假设上下梁任意截面x处的轴向力和内力矩分别为(FN1,M1)和(FN2,M2),则它们可表示为

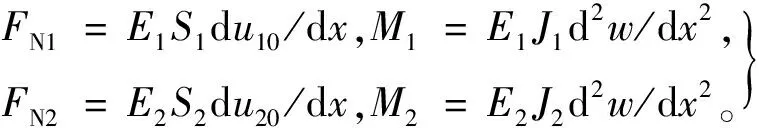
(6)

其中:S1,S2分别是上下梁横截面面积;J1,J2分别是上下梁截面关于其各自中性轴z1,z2的截面惯性矩。

从上下梁上分别截取微元体进行受力分析如图2所示,容易推出轴向力FN1,FN2与剪应力τ之间满足如下方程组

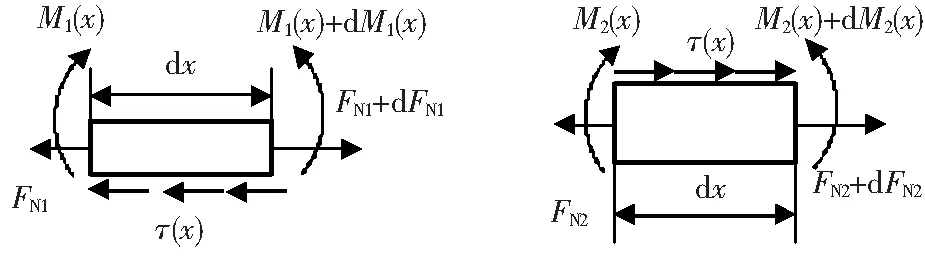
图2 上下梁微元体受力分析

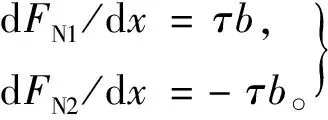
(7)

由合力矩定理,对胶合梁截面的分界线取矩(忽略胶层的厚度)可得组合梁整体截面上的总内力矩M(x)为

M=M1+M2-h1FN1/2+h2FN2/2,

(8)

其中,M是任意截面上的总内力矩。

综合考虑式(5)—(8)可得位移函数u10,u20,挠度w(x)和内力矩M(x)满足的微分方程组如下所示

另外,根据内力矩M(x)与分布载荷q(x)之间的微分关系d2M(x)/dx2=q(x),对式(9)中的第三个方程两边关于x连续微分2次得

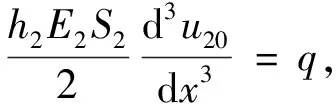
(10)

由式(9)容易得到

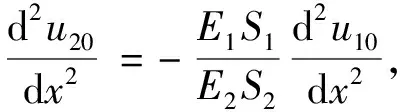
(11)

将(11)式两边关于x微分一次得

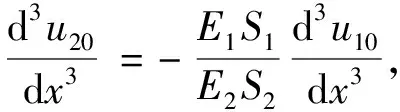
(12)

将式(12)代入式(10)中整理得

对式(9)中的第一个方程关于x连续微分3次有

(14)

其中,w(4)是挠度函数w(x)关于x的四阶导数。

将式(12)和式(13)代入式(14)中整理得

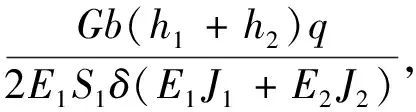
(15)

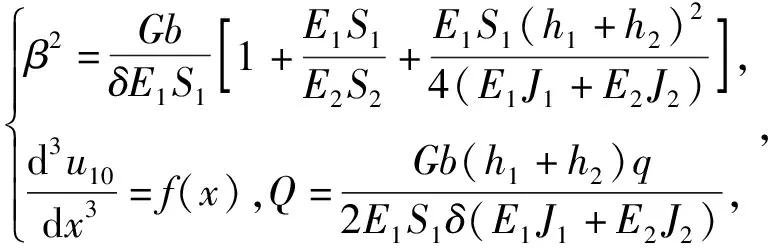
d2f/dx2-β2f=Q,

(16)

方程(16)的解为

f(x)=Ach(βx)+Bsh(βx)-Qβ-2,

即

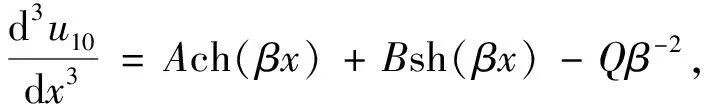
(17)

连续对方程(17)关于x积分3次有

u10(x)=β-3[Ash(βx)+Bch(βx)]-

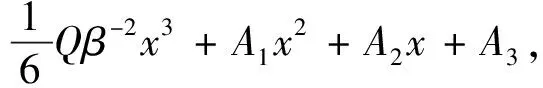
(18)

其中,A,B,A1,A2,A3是待定积分常数。

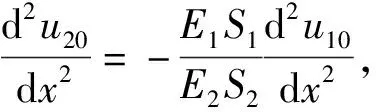
u20(x)=-χ{β-3[Ash(βx)+Bch(βx)]-

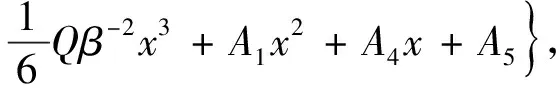
(19)

其中:A4,A5是积分常数,χ=E1S1/(E2S2)。

将式(17)代入方程(13)中有

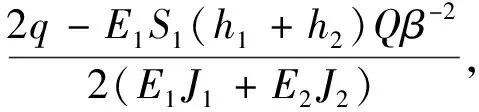
(20)

方程(20)的解为

w(x)=ζβ-4[Ach(βx)+Bsh(βx)]+

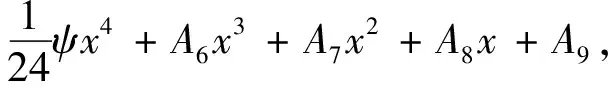
(21)

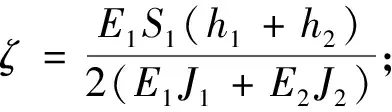
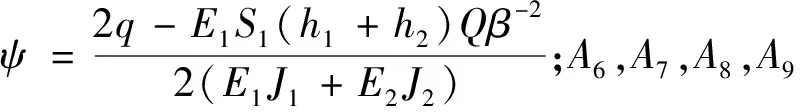
问题的边界条件为

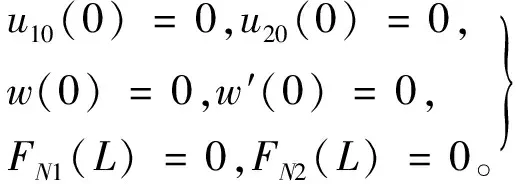
(22)

将式(18)、式(19)和式(21)代入式(22),可得如下方程组

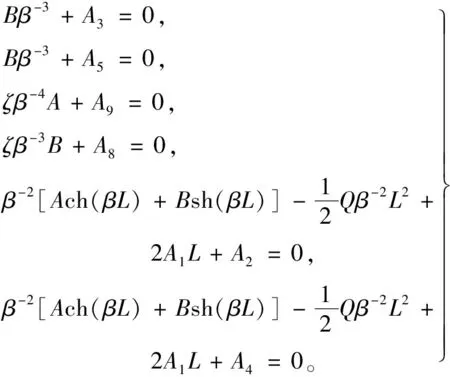
(23)

另外,由于胶接梁任意截面x处的总内力矩为M(x)=(L-x)2q/2,将该结果代入式(9)中的第三个方程有

(L-x)2q/2,

(24)

将式(18)、式(19)和式(21)代入方程(24)中,通过x的次幂同类项比较,可得如下待定系数方程组

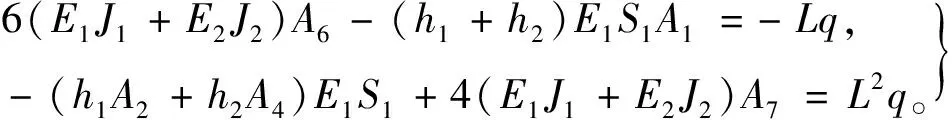
(25)

最后,对于胶接梁任意截面x处,位移函数u10(x),u20(x),w(x)还应满足式(9)中的第一个方程,同样利用x的次幂同类项比较,可得待定系数方程组

(26)

联合求解方程组(23)、(25)和(26)得到待定系数A,B,Aj(j=1,2,…,9)结果如下

(27)

将式(27)代入下列方程组(28)就最终确定了轴向位移u10(x),u20(x)、挠度w(x)和剪切应力τ(x)的具体表达式

(28)

2 算例与分析

假设L=0.9 m,b=0.055 m,h1=0.065 m,h2=0.085 m,E1=2.0×109N/m2,E2/E1=0.5,1.5,2.5,3.5,胶层厚度δ=0.000 2 m,剪切模量G=2.5×107N/m2,q=200 N。计算结果给出了在其他条件不变的情形下,梁挠度w(x)、胶层剪切应力τ(x)和上下梁形心线上点的位移u10(x),u20(x)随梁不同材质E2/E1比和截面位置x的变化情况,如图3—6所示。从图3看出,胶接梁挠度w(x)随E2/E1的增大呈递减变化,但又随着x的增大而增大,这符合悬臂梁变形的特点;从图4看出,在这4种材质组合下,胶接梁胶层内的剪切应力τ(x)呈现相似规律变化,即都有一个明显的峰值,位于[0.041,0.065]m之间,而在该峰值前后大体呈现直线规律变化,并且在x=L处为零,这是符合胶接梁在该处无剪切应力的边界条件的;此外,随着E2/E1比的增大,该峰值呈下降趋势。从图5和图6看出,随着E2/E1比的增大,上下梁形心线上点的位移值呈减少趋势,但对一定材质组合来说,它们的绝对值又随着截面位置参数x的增大而增加;另外,图5说明了上梁形心线发生压缩变形,悬垂端变形最大;图6说明下梁形心线发生了拉伸变形,悬垂端拉伸变形最大。图7说明了当胶层厚度为δ=0.000 2 m时,胶层界面剪切应力的变化情形,剪切应力峰值更偏向梁的固定端。

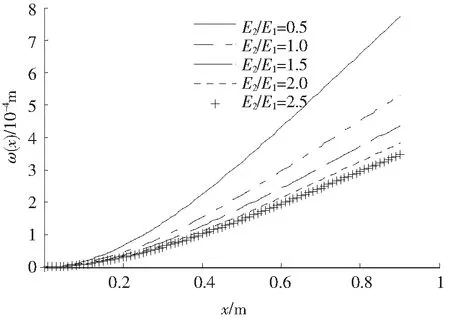
图3 胶接梁挠度随不同材质组合和截面位置的变化

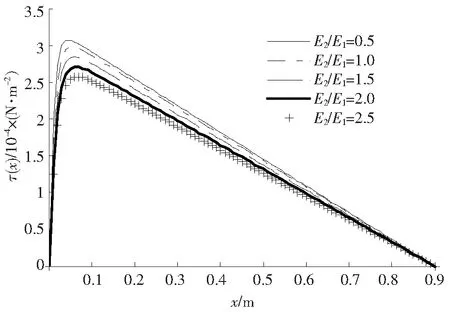
图4 胶层剪切应力随不同材质组合和截面位置的变化

图5 上梁形心线轴向变形随不同材质组合和截面位置的变化

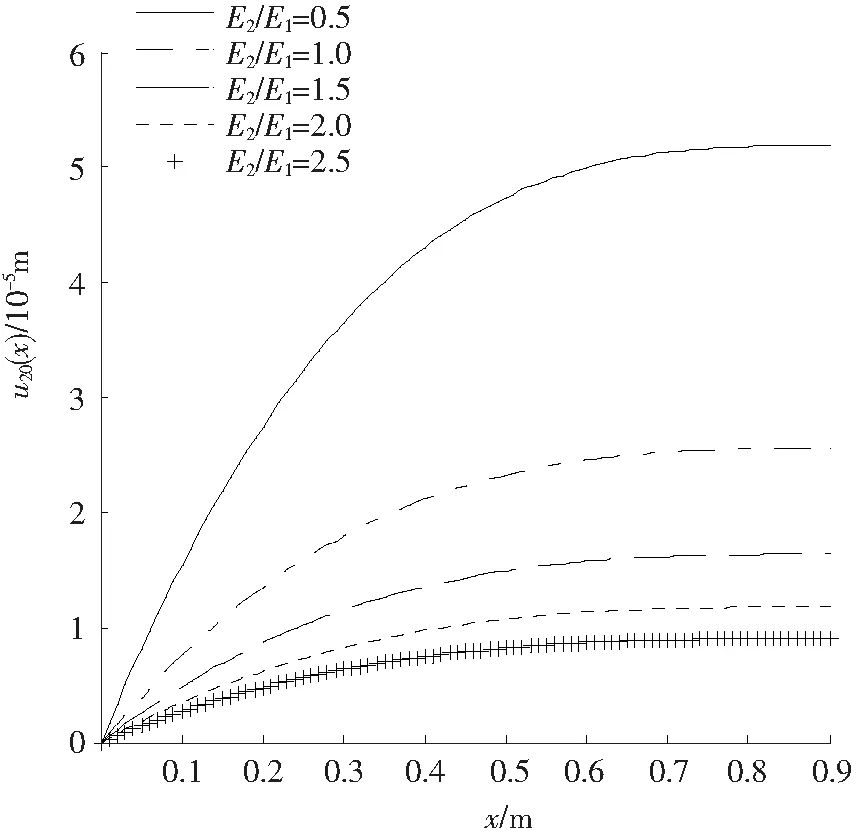
图6 下梁形心线轴向变形随不同材质组合和截面位置的变化

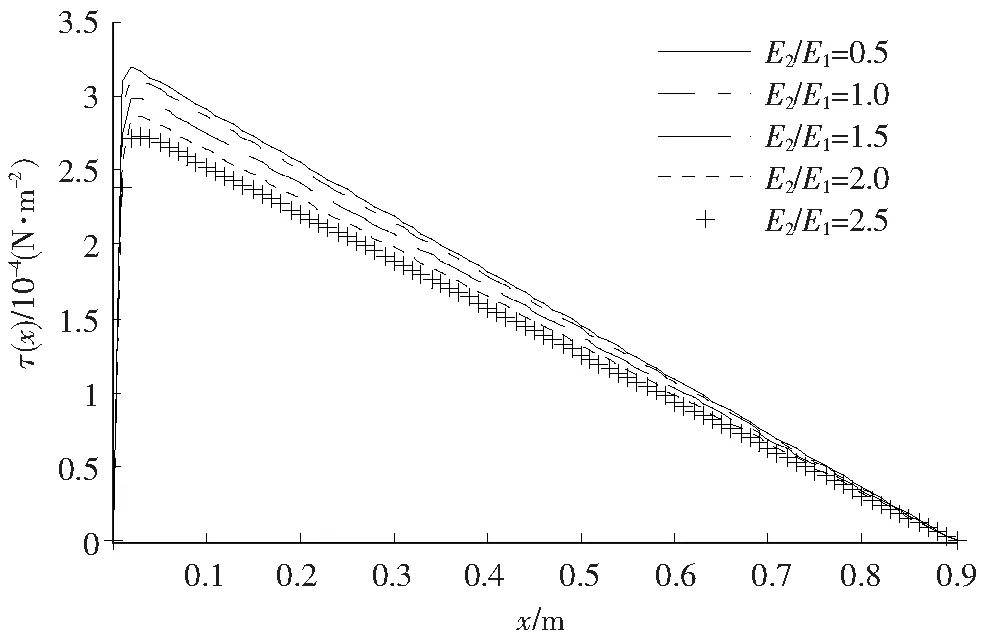
图7 胶层厚度为时其边界剪切应力随不同材质组合和截面位置的变化

3 结束语

根据上述理论分析和算例结果可得如下结论:

(1)对不同材质胶接成的组合悬臂梁,在均布载荷作用下,胶层内的剪切应力不为零,在靠近梁的固定端附近的一定范围内剪切应力较大,增加也比较快,是容易发生剪切破坏的地方。

(2)随着下梁与上梁杨氏模量比E2/E1的增大,胶接梁的挠度逐步减少,但梁的挠度沿着梁的长度方向却总是单调增加的,这与悬臂梁的变形特点吻合。

(3)对于胶接梁来说,在其下梁受到均布载荷作用时,上梁形心线承受压缩;下梁形心线承受拉伸。

(4)从计算结果看,在本文受载条件下,上下梁杨氏模量比越小,胶合梁的强度和刚度性能就越好,这是采用胶合工艺的重要原因之一。