月牙形空腔结构金属靶的抗弹性能分析*

高伟韬，彭克锋，张永亮，郑 航，赵 凯，郑志军

（中国科学技术大学近代力学系中国科学院材料力学行为和设计重点实验室，安徽 合肥 230027）

防护装甲是装甲车辆抵御冲击载荷作用的重要部件，对其进行轻量化设计是现代防护领域的重要发展方向，旨在满足机动性能、载重能力等要求的同时能够保证良好的防护性能。在防护装甲设计中引入空腔结构，可能在一定程度上实现对装甲车辆的减重，并通过引入新的抗弹机制来提高防护装甲的抗侵彻性能。

在均质钢板中加工一定数量规则排布的圆形贯穿孔洞，可以在侵彻过程中达到磨蚀和偏转子弹的效果[1]，并且合理的靶板尺寸和安装方式能够有效提高靶板的抗弹能力[2]。穿甲弹打击方形和圆形孔洞金属靶板的破坏形貌和防护系数差别不大，而孔洞的大小与弹径相当时靶板的抗弹性能最好[3-4]。实验和数值模拟研究表明，孔洞的存在使得弹着点在孔洞之间时靶板的防护性能比弹着点在孔洞中心时高得多[5-6]，而当子弹以一定倾角打击多孔金属板时能够减弱弹着点的影响并提高靶板的防护性能[7]。综合考虑，将具有合适尺寸孔洞和孔间距的多孔金属板以一定角度放置，能够最大程度发挥其抗弹效果[8]。在应对小口径动能弹丸侵彻时，多孔金属板表现出了优异的防护性能。针对多孔金属板的弹体侵彻问题，通过调整靶板孔洞形状、尺寸、弹着点等因素可以使得子弹发生显著磨蚀和偏转，在降低靶板重量的同时提高了靶板的防护性能。

传统多孔金属板是在成形均质钢板的基础上加工形成贯穿孔洞，因而限制了空腔的形状。随着3D 打印工艺的发展[9]，更复杂的金属内部结构可以通过增材制造的方式加工形成[10]，为空腔结构金属装甲设计提供了新的可能。本文中提出一种含有月牙形空腔结构金属靶板，研究其在侵彻过程中对弹体的偏转效果，探讨孔洞形状、尺寸以及弹体弹着点等因素对该靶板抗弹性能的影响。

1 数值模拟

1.1 靶板结构

靶板整体由面板和背板构成，如图1 所示。面板为含空腔的结构，厚度为H1；背板为均质603 装甲钢，厚度H2=40 mm。子弹为12.7 mm 穿甲燃烧弹（12.7 mm armor-piercing incendiary projectile, 12.7API）的弹芯，直径D=10.8 mm，长度L=52 mm，总质量为29.7 g。本文中主要研究弹体在空腔结构中的偏转效果，弹芯在侵彻过程中近似为刚体。子弹弹芯以818 m/s 的初速度正向侵彻空腔结构。

通过引入月牙形孔洞，设计了两种空腔结构，并依据其厚度方向中间截面是否具有对称性，分为对称结构和非对称结构，分别对应图2(a)和图2(d)中的几何模型，视图中结构上部分采用了透视化处理。S-1 和S-2 分别为经过对称结构和非对称结构在厚度方向上中点的截面，截面上的结构如图2(b) 和图2(e)所示。对称空腔结构中空腔几何形状及其参数如图2(b)所示，月牙形孔洞由两个直径为d 的球形偏移形成，偏移距离为δ，偏离度α=δ/d。α=0 时，两个球恰好重合，此时没有月牙形空腔；α=1 时，两个球恰好相离（外切），此时空腔为球形。同时定义一个无量纲参数β=δ/D，表征空腔相对于弹径D 的大小。一系列月牙形孔洞在空间上呈六角形排布，相邻两个空腔最小间距为1.0 mm。计算中，金属靶板的截面面积为50 mm × 50 mm，厚度H1=d + 2.0 mm。构成空腔结构的最小胞元为一个正六边形区域内的空腔和材料，如图2(c)所示，选取其中的9 个弹着点研究其对弹体偏转的影响。弹着点1 为胞元中心，即图2(b)中的圆心O1，弹着点2 为空腔中心，即图2(b)中δ/2 处。

图 1 弹体冲击空腔结构靶板的示意图Fig. 1 Schematic diagram showing a projectile impacting a cavity structure target

非对称空腔结构如图2(e)所示，其中虚线a、b 和c 为各个空腔胞元的球心O1的连线。在对称结构的基础上将虚线a 和c 上的空腔绕球心O1逆时针旋转90°，形成非对称结构。可以看到，相比于对称结构，对于非对称结构中一个胞元，其弹着点6～9 周围的结构变化较大，如图2(f)所示，因此以这些点研究非对称性对弹体偏转的影响。

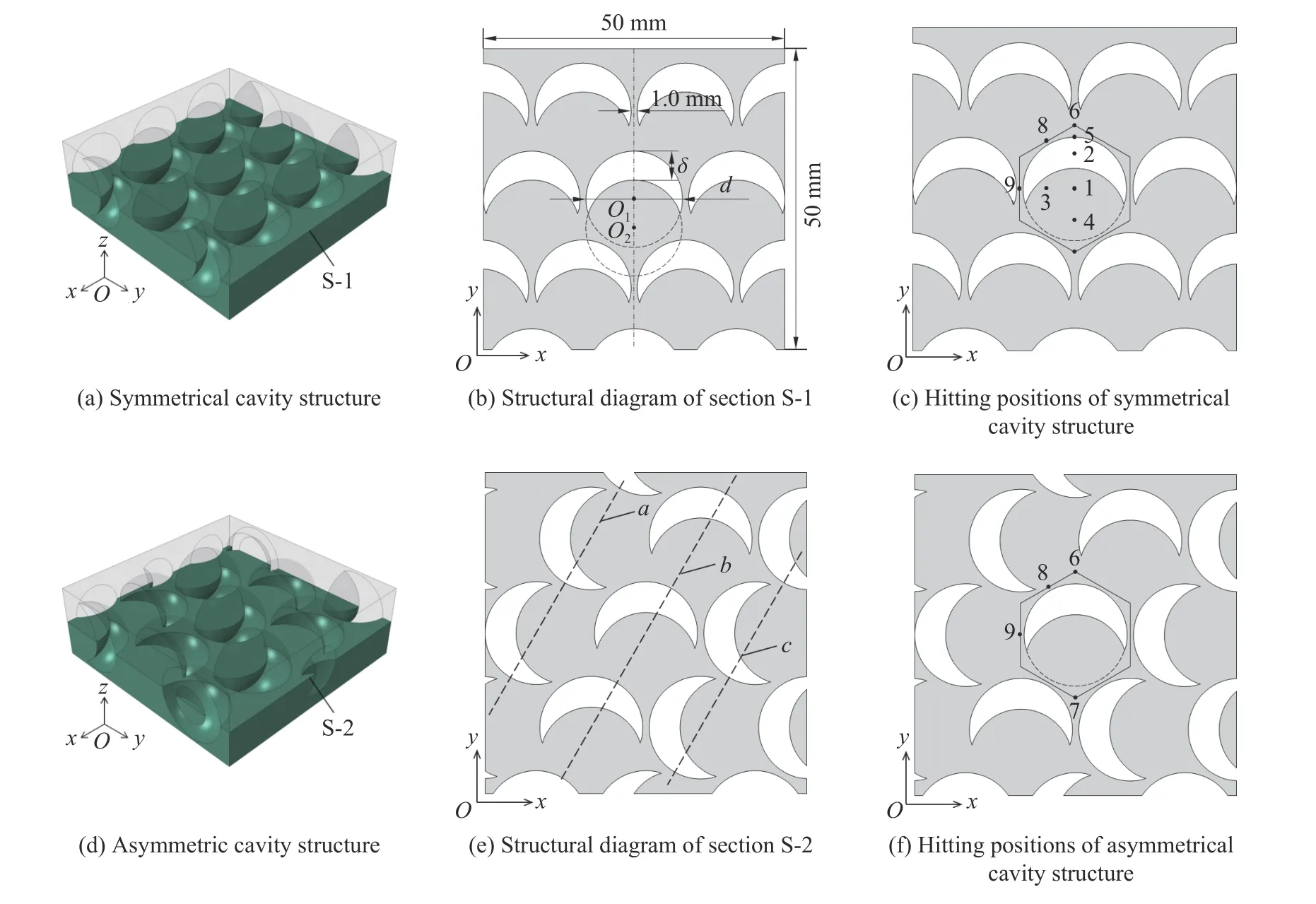
图 2 靶板几何结构和尺寸Fig. 2 Geometric structures and sizes of targets

1.2 材料模型

靶体材料为603 装甲钢，采用Johnson-Cook (JC)本构模型[11-12]模拟弹体侵彻过程中金属材料的动态力学行为，并且不考虑实际3D 打印加工对材料性质的影响。JC 模型在动态有限元模拟中被广泛使用，它给出了大变形下应变率和温度效应较简单的形式，流动应力σs的表达式为：

式中：ρ0为材料密度；c0为波速；s1为线性Hugoniot 系数；γ0为Grüneisen 材料常数；μ=1 - V∕V0为压缩体应变，V 为当前体积，V0为初始体积；Em为单位质量的内能。材料参数具体数值见表1。

表 1 603 装甲钢材料模型参数[13]Table 1 Material model parameters of 603 armor steel [13]

1.3 有限元模型

12.7API 侵彻空腔结构靶板的数值模拟使用Abaqus/Explicit 求解器进行分析，有限元模型如图3 所示，靶板四周固支。子弹材料在实验中表现出很高的强度，Iqbal 等[14]通过详细的力学试验得到了12.7API 弹芯的JC 模型参数A=1 658 MPa, B=20 856 MPa 和n=0.65。相比于603 装甲钢，弹芯材料具有较高的屈服强度和硬化特性，因此本文的数值模拟中将弹体作刚性假设。基于体素模型构建了空腔结构靶板的有限元模型，即先对均质模型划分单元，再通过删除空腔所在位置处的单元来近似地得到空腔结构。根据网格收敛性分析，网格尺寸定为0.5 mm，单元类型为八节点减缩积分体单元（C3D8R）。子弹和靶板之间设置通用接触，摩擦因数为0.2。定义侵彻过程中弹体的轴线和打击方向的夹角为θ，角速度为ω，如图4 所示，并提取在弹体侵彻过程中θ 和ω 随时间的变化曲线和最大偏转角度θmax，用来分析不同空腔结构对子弹的偏转效果。

图 3 弹靶有限元模型Fig. 3 A finite element model for a projectile and a target

图 4 弹体偏转角度和角速度计算Fig. 4 Calculation of deflection angle and angular velocity of the projectile

月牙形空腔结构靶板加工难度较大，采用12.7 mm API 弹芯侵彻60 mm × 60 mm× 60 mm 均质603 装甲钢靶工况验证模型有效性，弹靶变形如图5 所示，其中弹体为刚体。弹体最终侵深为30.0 mm，实际弹道测试中侵深为31.5 mm[15]，相对误差约为4.8%。数值模拟结果和实验结果吻合较好，验证了模型的有效性。

2 结果与讨论

图 5 刚性弹侵彻603 钢靶的变形图Fig. 5 Deformation diagram of a 603 steel target impacted by a rigid projectile

2.1 偏离度的影响

空腔形状由球径d 和偏离度α 控制。首先考虑弹着点1，对α 取0.1～0.7 和d 取8～24 mm的对称空腔结构进行了侵彻模拟。图6 为d=16 mm 和α=0.3 时弹靶在不同时刻的运动和变形情况，改变α 值得到弹体偏转角度和角速度随时间变化的曲线如图7 所示。

结合图7 中角度和角速度随时间的变化曲线，弹体偏转角度θ 随时间变化可分为3 个阶段：在0～t1时间段，ω 基本为零，此时θ 也基本为零；在t1～t2时间段，ω 近似以线性的方式增大，并在t2时刻达到最大值，此时θ 迅速增大；在t2～t3时间段，ω 由最大值逐渐减小，最终在t3时刻减小到零，此时θ 缓慢上升至最大值θmax；在t3时刻之后，弹体发生反弹现象，之后靶板对弹体偏转没有影响或者影响很小可以忽略。对于d=16 mm 和α=0.3 时，图6 中4.8、27.2 和60.8 μs 等3 个时刻分别对应图7(b)中的t1、t2和t3。可以看出，子弹在t1=4.8 μs 时偏转角度约为零，此时子弹头部刚好处于材料-空腔界面处，弹体两侧压强分布差异很小。后续侵彻中由于结构的不对称导致压强分布有了较大差异：主要是一侧受较大的压强，且压强最大值和主要受压区域在同一侧。弹体受力不平衡，偏转角速度从零逐渐增大。在t2=27.2 μs时，子弹恰好穿透靶板的空腔层，此时月牙形空腔基本上被子弹填充，弹体偏转角速度达到最大。随后由于背板的阻力弹体两侧受压区域差异开始减小，同时压强最大值移动到弹体另一侧，使得弹体的受力开始阻碍偏转，角速度逐渐减小，但是弹体偏转角度在一直增大。到t3=60.8 μs 时弹体两侧的压强分布差异已经较小，偏转角速度减小为零，偏转角度达到最大，此时θmax=11.5°。

图 6 靶板(d=16 mm, α=0.3)的变形和压强云图Fig. 6 Deformation and pressure cloud of the target with d=16 mm and α=0.3

考虑d=16 mm 以及弹着点为1 号位置，α=0.1，0.2，0.3，0.4，0.5，0.6，0.7 对应的子弹最大偏转角θmax分别为3.5°、8.8°、11.5°、11.1°、9.0°和2.3°，对应时刻的靶板变形如图8 所示。θmax整体趋势呈先增加后减小，在α =0.3 时达到最大值。从图9 中月牙形状随α 的变化可以看出，随着α 的增大，弹着点对应的球心O1逐渐从位于材料中向位于空腔中过渡，当α＞0.5 时之后O1一直处于空腔中。根据上面的结果，子弹在穿过材料-空腔界面时由于受到不对称力的作用而发生偏转。当α 较小时，空腔体积很小，在侵彻过程中很快被填充，子弹没有发生较大偏转的可能。当α 较大时，子弹侵彻过程中并没有穿透材料-空腔界面，而总是在一侧，导致不对称力较小因而不会有较大偏转。从图10 中各个球径d 下θmax随α 变化的曲线可以看出，不论d 为多大，θmax随α 的变化趋势都是先增大后减小，并在α 近似取0.3 时达到最大值。

图 7 偏离度α 对子弹偏转角度和角速度的影响Fig. 7 Influence of deviation degree α on the deflection angle and angular velocity of a projectile

图 8 含有直径为16 mm 的月牙形孔洞的靶板在不同偏离度时的变形Fig. 8 Deformation of the target with a 16-mm-diameter crescent-like hole at different deviation degrees

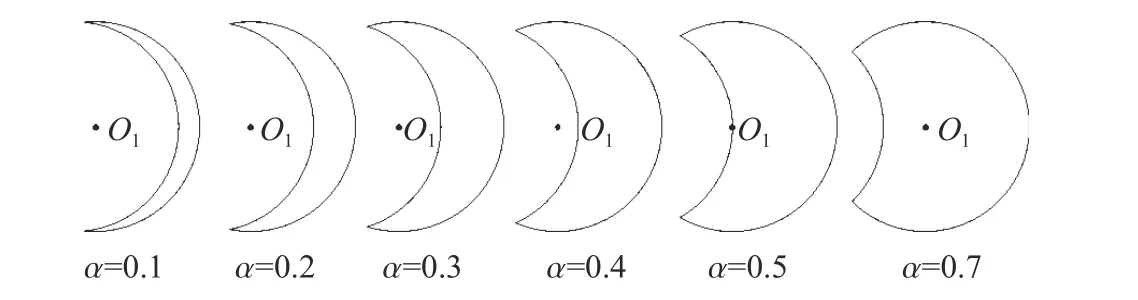
图 9 不同偏离度时的月牙形状Fig. 9 Crescent shapes at different deviation degrees

图 10 不同球径时子弹最大偏转角度随偏离度的变化曲线Fig. 10 Change of the maximum deflection angle with deviation degree at different sphere diameters

2.2 球径d 的影响

考虑对称空腔结构，当α=0.3，弹着点为1 号位置时，改变d 值，侵彻结束后靶板的最终变形如图11所示。随着d 的增大弹体偏转逐渐增大，背板上的残余侵深由于面板厚度的逐渐增加而逐渐减小。当d 大于20 mm 时可以发现，子弹在侵彻过程中已经不能完全填充空腔。进一步地，同时改变α 和d 的值，得到弹体最大偏转角θmax随α 的变化曲线，如图10 所示。对于固定的α 值，θmax总是随着d 的增大而增大。对于弹着点1，α 在0.3 附近的空腔结构对子弹的偏转效果最好，并随着球径d 的增大而提升，但过大的d 会导致结构中空腔体积占比增大，进而降低靶板的整体防护性能。

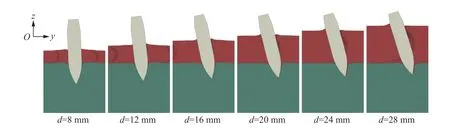
图 11 α=0.3 时靶板的变形Fig. 11 Deformation of targets at α=0.3

在靶板设计中，需要在保证空腔结构偏转性能的基础上提升其整体防护性能，即要提升靶板最弱处的防护性能。由于空腔结构中空腔部位的材料相对其他位置要少，可能导致空腔位置附近的防护性能低于其他位置。弹着点2 的位置在xOy 面和yOz 面的位置分别如图2(c)和图12所示，处于xOy 面偏移量δ/2 处，使得子弹侵彻时经过月牙截面面积最大的位置，此时参与抵抗子弹的材料最少，故以这个位置作为靶板最薄弱的位置进行分析。弹着点2 的防护性能显然和δ 的值相关，在偏离度不变时其大小受无量纲参数β 控制，需进一步考察β 对偏转性能的影响。

当α=0.3 以及弹着点为2 号位置时，对不同的d 的空腔结构模拟了子弹打击靶板的过程，得到侵彻过程中子弹的θmax随β 的变化曲线，如图13 所示。θmax随着β 的增大先是以线性上升，当β 达到0.5 附近时θmax为7°左右，之后在7°上下浮动。α=0.3 时，d=16 mm 得到β=0.44，d=18 mm 得到β=0.56。由此可以得出，当α=0.3，弹着点为2 号位置，β 逐渐增大时，空腔结构对子弹的偏转效果先是逐渐增大，β＞0.5 后偏转效果不会有明显改变且防护性能必然会逐渐降低，所以合适的空腔结构应该保证β 在0.5 附近，因而当d 在16～20 mm 范围内比较合适。

图 12 弹着点2 示意图Fig. 12 Diagram of hitting position 2

图 13 α=0.3 时θmax 随β 的变化曲线Fig. 13 Change of θmax with β at α=0.3

2.3 对称性对偏转效果的影响

选定α=0.3 和d=16 mm，以对称空腔结构（symmetric cavity structure，SS）的3～9 号弹着点和非对称空腔结构（asymmetric cavity structure，AS）的6～9 号弹着点进行弹体侵彻数值模拟。在子弹侵彻过程中，最大偏转角θmax在不同结构和弹着点的值如图14 所示。在6～9 号弹着点处，弹体偏转角度θ 的对比如图15 所示，对应弹体偏转的俯视视角如图15 所示，图中红色箭头表示弹体偏转时弹头的朝向，视图中靶板做透视化处理。

图 14 不同弹着点时弹体最大偏转角Fig. 14 The maximum deflection angles of the projectile at different hitting positions

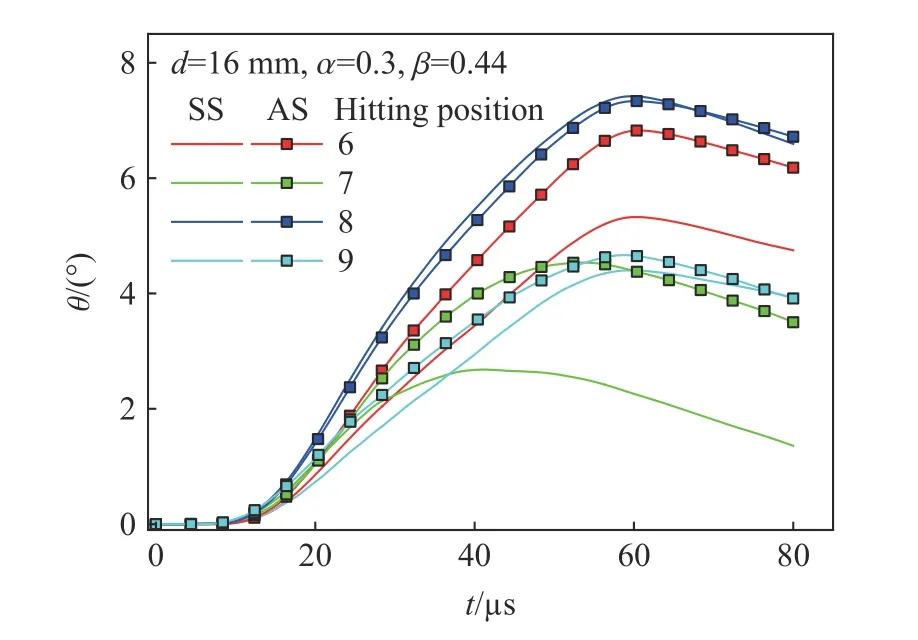
图 15 弹体偏转角随时间的变化Fig. 15 Change of deflection angle of projectile with time

从图14 中可以看出，θmax在不同打击位置时有明显的差别：1 号弹着点θmax最大，为11.5°；而4、6、7 和9 号弹着点θmax较小，均在6°以下。结合图2(c)中各个弹着点位置可以发现，4 号弹着点周围材料较其他位置更多，子弹侵彻过程中不会穿透材料-空腔界面，所以子弹头部受力较均衡，使得偏转角度较小。6，7 和9 号位置在空间位置上处于空腔胞元与胞元之间最薄弱的位置附近，同时也在xOy 面对称轴上，即空腔胞元在空腔排布上的对称性可能对弹体偏转有影响。

对比6～9 号弹着点对称和非对称空腔结构弹体侵彻过程中的θ 和θmax，非对称空腔结构在6 号和7 号位置上对弹体的偏转较对称空腔结构有1°～2°的提升，在8 号和9 号位置基本保持不变或者略有提升。图16 给出了弹体偏转的俯视图，其中红色箭头表示弹体偏转时弹头在xOy 面的朝向。结合图2(c)和图2(f)中可以发现非对称化处理主要改变了6～9 号位置周围原本的材料结构，在xOy 面完全失去对称性。非对称化使得6 号位置弹头朝向（红色箭头）的反方向上的材料增加，能够提供更大的作用力，使得子弹在侵彻过程中更容易偏转。7 号位置弹头朝向的空腔区域变大了，使得子弹能够在这一侧受到的力变小，偏转角度也变大。8 号和9 号位置周围结构的变化对弹体偏转的影响较小，其中弹体在8 号位置的偏转方向和角度大小都没有明显差异，在9 号位置方向发生明显变化，但偏转角度变化很小。综上可以得出，非对称结构较对称结构在偏转性能上有所提升。

图 16 弹体偏转俯视图Fig. 16 Top views of projectile deflection

3 结 论

采用Abaqus/Explicit 求解器模拟了12.7API 芯侵彻月牙形空腔结构的过程。研究表明，月牙形空腔结构对子弹有明显的偏转效果，通过对不同月牙形状和空间排布的数值分析，得到以下结论。

（1）月牙形空腔结构在靶板内部形成了大量且复杂的材料-空腔界面，使得子弹在穿过界面时由于两侧受力不平衡和材料变形的不协调而发生偏转，并对后续的侵彻过程产生影响，最终产生较显著的偏转效果。

（2）月牙形状对月牙形空腔结构的偏转效果有显著影响。随着构成月牙形结构的两球的直径d 的增大，弹体偏转角度也增大，并且在偏离度约为0.3 时达到最大的偏转效果。综合考虑靶板的偏转性能和防护性能，应该保证无量纲参数β 在0.5 附近时，此时d=18 mm。

（3）不同打击位置下月牙形空腔结构偏转效果有明显的差异，处于空腔胞元与胞元最薄若位置附近的弹着点对子弹偏转效果弱于其他位置。对空腔结构非对称化处理能够提升靶板的整体偏转效果，使得部分弹着点对应的弹体偏转有1°～2°的提升。