第三型应变时效的提出与研究进展*
王建军,袁康博,张晓琼,王瑞丰,高 猛,郭伟国
(1. 太原理工大学机械与运载工程学院,山西 太原 030024;2. 西北工业大学航空学院,陕西 西安 710072)
在对金属材料在很宽温度、很宽应变率范围内的塑性流动行为进行测试时,会发现:在相同的应变率下,随着温度的升高,流动应力应变曲线不会出现我们通常认为的下降,而是会整体曲线或较大部分反而上升,如图1(a)所示,图中T1、T2和T3分别为三条应力应变曲线的试验温度,表现在对应的流动应力-温度曲线上为出现一反常应力峰[1-6]。这种金属材料随温度升高出现的强化现象与塑性变形中的Portevin-Le Chatelier(PLC)动态应变时效类似,即应变和时效同时发生,都属于动态应变时效现象,但是二者的宏观表现完全不同,PLC 动态应变时效表现为应力-应变曲线上的锯齿流动现象[7],如图1(b)所示。动态应变时效现象的发现最早可以追溯到Le Chatelier 在1909 年在低碳钢的高温变形中首次发现了锯齿流动现象,之后Portevin 和Le Chatelier 在“硬铝”的常温变形中发现了相似现象,这种锯齿流动现象从此被命名为PLC 效应[7]。鉴于这种流动应力随温度变化在曲线上出现的反常应力峰现象在形式上有别于静态应变时效[8-9](见图1(c))和PLC 动态应变时效,Wang 等[6]在2015 年首次将这一现象命名为“第三型应变时效”(third-type strain aging,简称3rd SA)。学者们在研究多种金属材料的塑性流动行为中均发现了类似的反常应力峰现象,并沿用了第三型应变时效这一命名[10-15]。第三型应变时效现象的出现具有普遍性,不仅在BCC、FCC 和HCP 多晶金属中发现了这一现象[16-20],而且在单晶金属中也出现了这一现象[21-23]。

图 1 三种应变时效的表现形式Fig. 1 Manifestation of the three kinds of strain aging
第三型应变时效现象的发现,使得传统的金属材料力学性能随温度升高出现热软化及其相关位错的热激活理论不能准确解释金属材料力学行为随温度的变化规律。常见的经验型本构关系和基于位错热激活理论的物理概念本构关系都不能很好地描述金属的塑性流动行为。为此,本文中从第三型应变时效现象的宏观特征、微观机理以及考虑第三型应变时效的本构关系三个方面来系统介绍第三型应变时效。
1 第三型应变时效现象的宏观特征
为了直观地分析第三型应变时效现象,将不同温度下的应力应变曲线转换为流动应力随温度变化的曲线,可以发现:在同一应变率下,随着温度的升高,流动应力先减小,当温度达到某一值时,流动应力随着温度的升高出现了反常的增长,直至达到一峰值应力,随着温度的继续升高,流动应力随温度的升高而下降。在某一温度区域内,流动应力随温度变化的曲线上出现了有第三型应变时效引起的反常应力峰,如图2[1,24]所示。对于奥氏体和铁素体不锈钢,在准静态下应力峰出现的温度范围约为0.3~0.5 倍的熔点温度[25],对于双相不锈钢,应力峰出现的温度为0.35 倍的熔点温度[26]。从图2 中可以看出,应力峰出现的温度随应变率的增大而移向更高温度。对于Q235B 钢,在0.001 s-1应变率下,应力峰出现的温度为0.31 倍的熔点温度;在800 s-1应变率下,应力峰出现的温度为0.52 倍的熔点温度;当应变率为7 000 s-1时,应力峰出现的温度为0.56 倍的熔点温度[6]。为了定量描述应力峰随应变率的变化规律,Guo 等[3]、Wang 等[6]、孟卫华等[27-28]建立了相关的物理模型。

图 2 不同应变率下流动应力随温度变化曲线Fig. 2 Variation of flow stress with temperature at different strain rates
第三型应变时效的出现往往伴随着PLC 动态应变时效现象,并且PLC 动态应变时效通常出现在应力峰上升部分对应的温度区域内[6,29-31]。根据PLC 动态应变时效引起的锯齿形状特征,通常把锯齿形状分为A、B、C 三种类型[32-34]。PLC 动态应变时效同时会引起试样表面出现局部的变形带(Luders 带),随着应力增大,变形带会沿着试样移动[34-35]。A 型锯齿波一般在较小的应变和较低的温度时出现,A 型锯齿波的一个重要特点是:Luders 带在逐渐升高的外力作用下向前移动;B 型锯齿波一般出现在较高的温度或较低的应变率下,并且Luders 带生成后并不扩展;C 型锯齿波的形状介于A 型与B 型之间,Luders 带生成后并不扩展,并且不断有新的Luders 带生成[34]。Sakthivel 等[36]通过对高温合金Hastelloy X 在宽温域、不同应变率下的锯齿流动行为进行测试,分析了温度和应变率对高温合金Hastelloy X 锯齿流动行为的影响。Roy 等[37]对奥氏体高温合金C-276 在宽温域、不同应变率下的锯齿流动行为进行了测试和分析,并通过透射电镜观察发现:锯齿流动出现时位错密度增大。Karabulut 等[38]通过改变中碳钢中钒的含量来研究钒含量对第三型应变时效的影响。Gündüz 等[39]研究了不同的热处理对第三型应变时效引起的反常应力峰的影响。Ganesan 等[5]研究了316LN 奥氏体不锈钢中氮含量对动态应变时效行为(包括锯齿流动出现的温度和锯齿流动出现的临界应变)的影响,并认为氮溶质原子是引起316LN 奥氏体不锈钢中出现动态应变时效的原因。Xiao 等[40]通过热处理来改变DH-36 钢中自由碳原子的含量,进而分析其对第三型应变时效引起的反常应力峰宏观特征的影响。Yuan 等[41]通过测试三种不同热处理状态下的激光金属沉积Inconel 718 合金在宽温度和应变率范围内的塑性流动行为,发现时效处理后沉淀强化合金材料的第三型应变时效引起的反常应力峰明显降低[41],沉积态合金的反常应力峰也随着应变率的升高而降低[42]。
2 第三型应变时效的微观机理
在金属的塑性变形过程中,位错的运动并不是连续的,它们在运动时将被暂时阻挡在短程障碍物(如溶质原子)之前,等待热激活以克服障碍物,再前进到下一个障碍物[43]。在位错在障碍前的等待期间,溶质原子向位错扩散,在位错周围形成溶质原子气团,对运动位错“钉扎”,阻碍了位错的运动(见图3),在宏观上表现为金属流动应力增大[44]。目前,对溶质原子扩散至运动位错周围的方式还存在争议。Cottrell 等[45]认为变形诱导的空位可以帮助溶质原子的扩散;Cuddy 等[46]、Schwarz 等[47]认为溶质原子借助林位错管道扩散至运动位错周围,形成溶质原子气团,对运动位错“钉扎”,而不需要借助于空穴,也就是说管道扩散是引起动态应变时效的主要机制。Picu 等[48]研究发现,如果不借助于空位,管道扩散的速度会太慢。对于钢,如果不含有足够的合金元素,如Al、V、Nb、Ti,则碳原子和氮原子不能全部形成碳化物和氮化物,因此,由于自由碳原子和氮原子与位错的相互作用,合金钢的塑性流动行为中会出现应变时效[6]。通过计算18-8 奥氏体不锈钢动态应变时效过程的激活能,Peng 等[49]发现:在低温下,动态应变时效是由C、Ni 溶质原子气团和位错的相互作用引起的,而在高温下,动态应变时效则是由C、Cr 溶质原子气团和位错的相互作用引起的。Cuddy 等[46]发现:对于铁基合金,置换溶质原子(O、Si、Mn、Ni、Ru、Rh、Re、Ir 和Pt)与位错的相互作用是引起动态应变时效的主要原因。对于镁合金AZ91,Al 原子被认为是引起动态应变时效的主要溶质原子,而Zn 原子被作为Al 原子扩散的催化剂[50]。
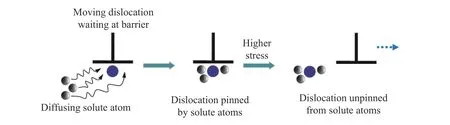
图 3 扩散的溶质原子对运动位错的钉扎引起的第三型应变时效的示意图Fig. 3 Schematic of third-type strain aging caused by dislocation pinning by diffused solute atom
由于热量可以为点缺陷的运动提供能量,因此,温度可以影响溶质原子和空位的运动,而应变率可以影响位错的数量和运动[51]。当温度和应变率达到某种关系时,在位错周围会形成溶质原子气团,“钉扎”位错,阻碍其运动[43,52]。在低温高应变率下,溶质原子的扩散速度低于对应的位错运动速度,第三型应变时效不会发生。在高温低应变率下,溶质原子气团随着位错运动,溶质原子的扩散速度高于对应的位错的运动速度,溶质原子气团不会对位错“钉扎”,第三型应变时效同样不会发生[45,53]。
早在19 世纪,人们就发现,在机械加工过程中,当低碳钢被加热到表面变蓝时会变得很脆,这一现象被称为“蓝脆”,原因在于,材料在塑性变形过程中,扩散的溶质原子对位错的钉扎,造成了材料变形阻力的增加。随着变形阻力的增加,材料内的应力水平也会更高,引起微裂纹的形成和增殖,最终导致材料韧性降低[25,54-55]。伴随着第三型应变时效引起的反常应力峰,材料的韧性也通常随温度升高而降低,即出现蓝脆现象,在该温度区域内,韧性随温度变化呈现一低谷[17,31,56]。对于BCC 铁,在出现蓝脆温度区域内,动态应变时效是由运动位错和碳或氮溶质原子的相互作用引起的[57]。Koyama 等[58]研究了不同碳含量对Fe-Mn-C 奥氏体不锈钢力学行为中表现出来的动态应变时效引起的蓝脆现象的影响规律。与应变率对第三型应变时效现象的影响相似,随着应变率的增大,蓝脆现象出现的温度区域移向更高的温度区域[31]。PLC 效应、第三型应变时效和蓝脆现象都是由运动位错与扩散的溶质原子的相互作用引起的,被认为是动态应变时效的三种表现形式[6]。
在动态应变时效的温度区域内,多种金属材料的内耗随温度变化曲线出现了Snoek 内耗峰[59]。Schwink 等[60]认为金属内耗峰产生的机理可用来解释PLC 效应。并且已有的研究结果表明,对于铁碳合金,当振动频率为1 Hz 时,内耗峰出现在470~590 K 的温度范围内[61-64],该温度范围与准静态下动态应变时效出现的温度范围接近。随着频率增大,内耗峰会移向更高的温度[63,65-66]。Wang 等[6]和郭伟国等[67]通过研究发现,内耗峰出现的温度随频率的变化规律与第三型应变时效出现的温度随应变率的变化规律相同。内耗峰和金属塑性变形中出现的第三型应变时效都是由相同的微观机理引起的,并且二者有着相似的宏观特征。因此,第三型应变时效被认为是机械波谱的另一种表现形式。彭开萍等[68]对3004 铝合金在“反常”锯齿屈服的温度区域进行了内耗试验,并结合激活能的计算、内耗研究、微观组织观察和能谱分析,探讨“反常”锯齿屈服的机理与物理本质。Lee 等[69]通过内耗试验分析了孪晶诱导塑性钢(Fe-18%Mn-0.6% C 和Fe-18% Mn-1.5% Al-0.6% C)在常温下出现PLC 锯齿流动的原因。Karlsen 等[70]通过对AISI 316 NG 奥氏体不锈钢进行不同温度下预应变后的内耗试验发现:在动态应变时效温度区域内预应变后的Snoek 内耗峰的高度显著增大。Ivanchenko 等[71]对退火后的镍基高温合金Inconel 600 进行了内耗试验,在620~670 K 温度范围内出现了碳原子引起的Snoek 内耗峰,而当对镍基高温合金Inconel 600 在动态应变时效出现的温度(423 K)下首先进行预拉伸,而后进行内耗试验时,发现其内耗峰明显增大。
综上所述,第三型应变时效、PLC 效应和蓝脆现象都是由运动位错与扩散的溶质原子的相互作用引起的,被认为是动态应变时效的三种表现形式。
3 包含第三型应变时效的金属热黏塑性本构模型
常见的描述金属塑性流动行为的热黏塑性本构模型可分为经验型/唯象本构模型和物理概念本构模型。经验型本构模型最常见的有Johnson-Cook 本构模型(J-C 模型)[72-74],J-C 模型是一种纯经验型或者半经验型本构模型,由于其形式简单而被广泛应用于工程实践中,并被嵌入到ANSYS、ABAQUS 等有限元软件中。物理概念本构模型主要包括Zerilli-Armstrong 模型(Z-A 模型)[75]、力阈值应力本构模型(MTS 模型)[76]、Bonder-Partom 模型(B-P 模型)[77]、Nemat-Nasser 物理概念本构模型[1-2,78-79]以及其他具有物理意义的本构模型[73,80],这些本构模型都已被认可和广泛应用。Z-A 模型是基于位错动力学的概念提出的、分别针对FCC 和BCC 金属的塑性流动本构模型,模型中考虑晶粒尺寸的影响。MTS 模型是基于位错的热激活运动理论建立的,它将流动应力和力阈值应力作为内状态变量与应变和应变率相关联。B-P 模型是基于连续介质力学和唯象学的基本概念建立起来的。Nemat-Nasser 物理概念本构模型是基于位错的动力学基本理论建立起来的,其将塑性流动应力分为热激活部分和非热部分。近几年,Gao 等[81]研究了FCC 金属在高应变率下运动位错密度的演化,并建立了相关的本构模型。Khan 等[82]建立了可以描述2024-T351 铝合金的依赖于温度和应变率的唯象本构模型。
研究表明,以上金属热黏塑性本构模型可以很好地描述金属材料在不同温度、不同应变率下的塑性流动行为,并且这些本构模型在工程中均得到了广泛的应用。但是,这些模型都没有考虑金属塑性流动行为中出现的第三型应变时效现象,也就是说,金属塑性流动行为出现的第三型应变时效现象使得现有金属热黏塑性本构模型均不再适用。为了能描述金属塑性流动行为中普遍存在的第三型应变时效现象,学者们基于运动位错与溶质原子的相互作用建立了可以描述该行为的物理概念本构模型[24,83],但是由于第三型应变时效过程较为复杂,使得建立的这类模型极为复杂。通常,这类模型会包含大量的参数,使得拟合过程也极为困难。为了能描述第三型应变时效对金属材料塑性流动行为的影响,唯象第三型应变时效模型被广泛采用[3,6,27-28,84-87]。Lee 等[86]建立了半经验型的第三型应变时效模型,但该模型并未考虑应变率对第三型应变时效的影响。Lee 等[85]和Guo 等[3]、孟卫华等[27-28]、Su 等[87]在Nemat-Nasser 物理概念本构模型的基础上,考虑了第三型应变时效的影响以及第三型应变时效随应变率的变化规律,建立了可以描述金属塑性流动行为中出现的反常应力峰现象的塑性流动本构模型,初步完善了金属热黏塑性本构模型。Shen 等[88]利用唯象第三型应变时效模型建立了可以描述金属各向异性、热软化和第三型应变时效现象的金属热黏塑性本构模型,如图4 所示。Wang 等[6]结合第三型应变时效发生的机理(即运动位错与溶质原子的相互作用)及其宏观特征,建立了包含第三型应变时效现象的金属塑性流动本构模型。图5 所示为本构模型预测得到的Q235B 钢的流动应力随温度和应变率变化的情况,从图中可以看出,第三型应变时效引起的应力峰如同“山脊”出现在时效温度区域内,并且随着应变率增大,应力峰高度降低,其出现的温度区域移向了更高的温度区域。郭扬波等[89]考虑位错与位错芯内的溶质原子(位错芯气团)的相互作用,在Z-A 热黏塑性本构模型的基础上,加入位错和位错芯气团的相互作用的影响,建立了一种可定量描述第三型应变时效现象的本构模型。Song 等[10]利用Wang 等[6]建立的第三型应变时效模型建立了包含第三型应变时效的金属热黏塑性本构模型。Song 等[11]、Voyiadjis 等[90-91]基于修正的Voyiadjis-Abed 模型建立了包含第三型应变时效的热黏塑性本构模型。Li 等[18]通过机器学习的方法确定了修正的J-C 本构模型,模型可以描述DP800 钢在不同温度和应变率下的塑性流动行为,但是文中所研究的温度范围为20~300 ℃,DP800 钢塑性流动行为并没有表现出完整的第三型应变时效,如图6 所示。Yuan 等[41]针对三种不同热处理状态下激光沉积Inconel 718 合金,将Wang 等[6]建立的第三型应变时效模型引入考虑热处理引起的微观结构演化的物理本构模型。拟合出流动应力的动态应变时效分量的本构参数,结合微观组织分析认为,沉淀强化金属材料中不同尺寸的沉淀相对第三型应变时效具有不同的影响机制。当运动位错切过尺寸较小的强化相时,强化相与钉扎原子的共同作用使第三型应变时效现象更为明显;而当运动位错绕过尺寸交大的强化相时,部分钉扎原子被保留在围绕强化相的位错环内,导致运动位错上钉扎原子浓度降低,从而减弱了第三型应变时效现象。
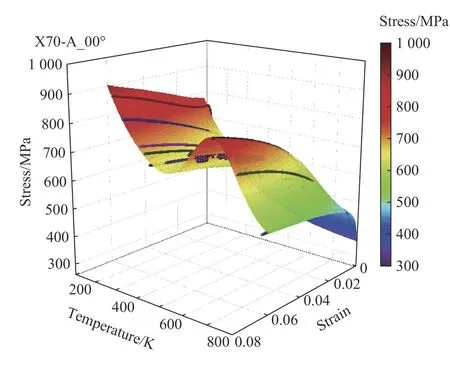
图 4 API X70 管线钢塑性流动行为中出现的第三型应变时效现象及本构模型预测结果[88]Fig. 4 Third type strain aging phenomenon in the plastic flow behavior of API X70 pipeline steel and prediction results of constitutive model[88]
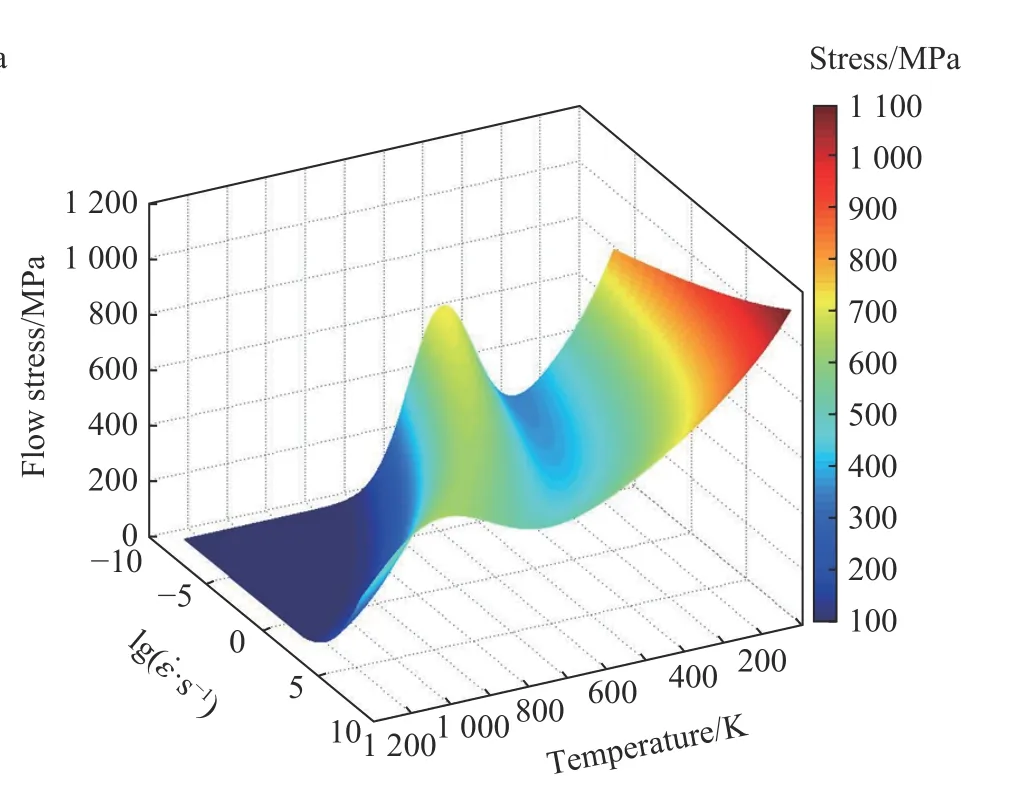
图 5 本构模型预测得到的Q235B 钢在应变为0.1 下的流动应力随温度和应变率变化的情况[6]Fig. 5 Constitutive model predicted variation of flow stress at the strain of 0.1 with temperature and strain rate for Q235B steel[6]
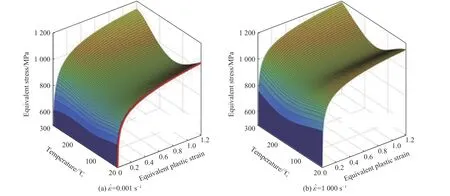
图 6 通过机器学习得到的DP800 钢的流动应力随温度和等效应变率变化的情况[18]Fig. 6 Variation of flow stress with temperature and strain rate obtained with machine learning for DP 800 steel[18]
4 结 论
随着金属材料的发展以及对晶体位错理论的不断认识,传统的金属材料力学性能随温度升高出现的热软化及其相关的位错的热激活理论并不能完全反映金属材料力学行为随温度的变化规律。通常认为金属材料的流动应力随着温度的升高而降低,但在金属材料的实际应用中或对金属材料力学行为进行试验测试时会发现,在某一温度范围内,其流动应力随温度变化的曲线上会出现一反常应力峰,即第三型应变时效现象。第三型应变时效被认为是由运动位错与扩散溶质原子的相互作用引起的,而溶质原子的扩散需要借助于空位或/和林位错管道。第三型应变时效、PLC 动态应变时效和蓝脆现象都是由运动位错与扩散的溶质原子的相互作用引起的,是动态应变时效的三种表现形式,并且第三型应变时效被认为是机械波谱的另一种表现形式。第三型应变时效现象的出现使得常见的本构模型不能描述金属的塑性流动行为,具有物理概念的包含第三型应变时效的本构模型由于形式过于复杂而并未得到广泛应用,而近几年基于第三型应变时效的机理和宏观特征建立的半经验型的包含第三型应变时效的本构模型受到了广泛重视。

