两种变厚度空心储能飞轮的应力特性
兰 晨,李文艳
(华北电力大学能源动力与机械工程学院,北京102206)
近年来,我国积极应对全球气候变化,践行《巴黎协定》,为实现“碳中和”而大力发展可再生能源,特别是太阳能、风能装机功率在2030 年将达到12 亿千瓦。但是可再生能源受各类因素所限制而有着较大的随机性与波动性,其并网过程会给电网带来一定的冲击[1]。应用储能装置可以很好应对可再生能源给电网带来的影响,其中飞轮储能由于充能速度快、响应时间短、占地小、无污染和使用寿命长等优点在新能源并网、UPS、石油石化、轨道交通等领域得到了广泛的运用[2-5]。
储能飞轮根据其拓扑结构主要可以分为4 种:内飞轮内转子结构、分体式结构、内转子外飞轮结构、外转子外飞轮结构[6]。其中内转子外飞轮结构可以视为轮辐加轮缘的变厚度空心飞轮结构,由于其大部分质量分布在飞轮外缘,使得其具有较大的储能密度,因此在商业上得到了广泛的应用[7]。目前,已有众多学者对此类飞轮结构进行了分析研究与优化设计。苏芳等[8]基于有限元软件分析研究了空心飞轮转子使用不同材料时飞轮径向、环向应力的变化规律。任正义等[9]应用Ansys Workbench 软件对3种不同形式的空心铝合金飞轮转子模型进行有限元分析,研究了3 种形式空心飞轮转子的应力、变形分布情况,并对曲线轮辐飞轮进行了优化。闫晓磊等[10]采用最优控制理论,得到空心飞轮转子的最优形状解析表达式,并对空心飞轮转子在低速、中速和高速情况下进行了最优化设计。以上飞轮转子应力分析都建立在平面应力状态假设的基础之上,并未考虑飞轮轮缘对应力分布,特别是轴向应力的影响,在飞轮轮缘高度较大时不能有效确定飞轮应力分布。因此本文建立了两种变厚度空心飞轮模型,在空间应力状态假设基础上,利用Ansys Workbench有限元分析软件分析了轮缘高度变化对两种飞轮模型径向、环向、轴向应力最大值及最大变形量的影响,并给出了沿给定路径的各项应力分布。
1 飞轮应力理论
目前的飞轮结构优化与应力研究大多建立在盘状飞轮的基础上[8-10],当飞轮外径R1与飞轮厚度h满足式(1)[11]时

飞轮应力状态可以视为平面应力状态,然而当飞轮结构不满足式(1)时,例如功率型储能飞轮大多采用半径小、高度大、转动惯量小,近似于空心长圆筒型的结构[4],此时不能采用平面应力理论计算飞轮的应力,将飞轮应力分解时需要考虑轴向应力,根据弹性力学理论,飞轮高速旋转产生的离心力可沿圆柱坐标系3个方向分解为径向应力、环向应力与轴向应力,对于各项同性的等厚度空心圆筒,其在半径为r 处的径向应力,环向应力与轴向应力分别为

式中,σr为飞轮径向应力,Pa;σθ为飞轮环向应力,Pa;σz为飞轮轴向应力,Pa;εz为飞轮轴向应变;ρ为飞轮材料密度,kg/m3;ω为飞轮旋转角速度,rad/s;v 为材料泊松比;R0为飞轮内径,m;R1为飞轮外径,m。
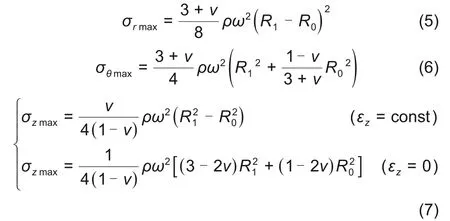
且明显可知飞轮环向应力始终大于径向应力与轴向应力,采用工程设计Tresca 屈服准则时,仅需满足

式中,[σ]为材料许用应力,Pa。
变厚度结构可将大部分质量集中在飞轮外径处。变厚度结构较于等厚度结构,其优势在于采用变厚度结构的飞轮有着较大的有效回转半径,等厚度飞轮与变厚度结飞轮结构如图1所示,其有效回转半径分别为
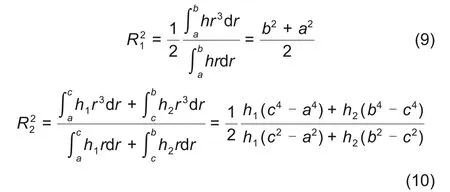
当h=h2时,式(9)减去式(10)有
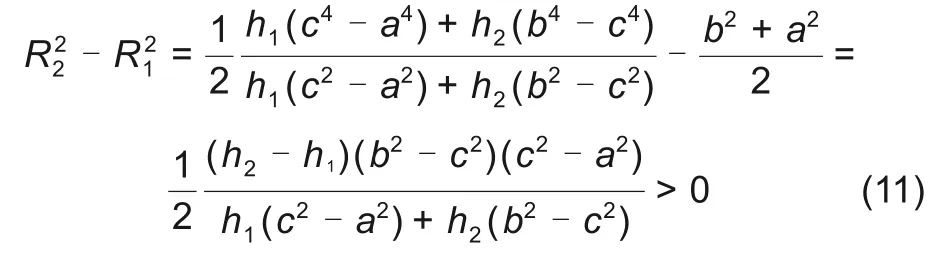
式中,h 为等厚度飞轮厚度;h1为飞轮轮盘厚度,m;h2为飞轮轮缘厚度,m;a 为飞轮内径,m;b为飞轮外径,m;c为飞轮轮缘内径。

图1 等厚度飞轮结构图(a)与变厚度飞轮结构图(b)Fig.1 Structure diagram of equal thickness flywheel(a)and variable thickness flywheel(b)
而飞轮储能密度通常由飞轮有效回转半径决定,通常情况下飞轮储能密度指质量储能密度,飞轮质量储能密度可表示为

式中,E为飞轮储能量,J;I为飞轮转动惯量,kg/m2;ω为飞轮角速度,rad/s;R为飞轮有效回转半径,m;K为飞轮形状因子;[σ]为许用应力,Pa。
图2 给出了飞轮形状因子与飞轮结构的关系,形状因子K越大代表飞轮储能性能越好。
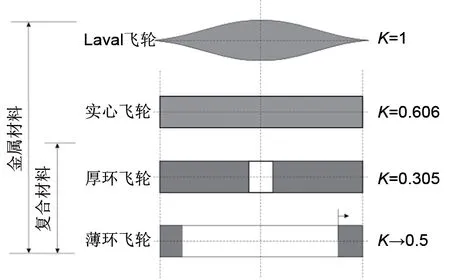
图2 不同飞轮结构的形状因子Fig.2 Shape factors of different flywheel structures
由图2 可以得知等厚度结构飞轮形状因子为0.305,而变厚度结构飞轮形状因子介于0.305~0.5 之间。由上述分析可知变厚度结构有着比等厚度结构更好的储能特性。
2 变厚度空心飞轮模型构建
在飞轮角速度与材料都确定时,飞轮应力仅与其结构有关,建立如图3的转子模型,其中X1代表轴孔半径、X2代表轮辐半径、X3代表轮缘厚度、X4代表轮缘高度、X5代表轮辐厚度,两种转子模型的结构参数见表1。将两模型导入有限元软件Ansys Workbench 中并施加10000 r/min 的旋转速度与合适的约束条件,为了同时考虑计算精度与计算速度,选取MultiZone 划分方法,网格长度取2 mm,划分网格后的飞轮转子模型如图4所示;为了分析轮缘高度对飞轮轮辐上应力分布的影响,建立从飞轮内径到外径的路径如图3 中A-B。飞轮材料使用7075铝合金,其参数见表2。
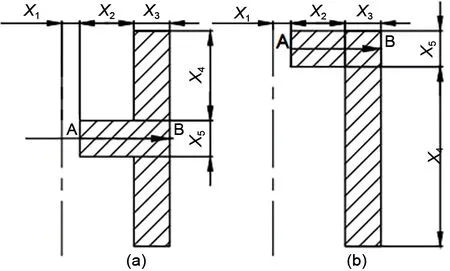
图3 飞轮模型一(a)与飞轮模型二结构图(b)Fig.3 Structure diagram of flywheel model 1(a)and flywheel model 2(b)

图4 X4=100 mm时飞轮模型一的有限元网格划分Fig.4 Meshing of flywheel model 1 when X4=100 mm

表1 飞轮转子模型参数Table 1 Model parameters of flywheel rotor

表2 飞轮材料参数Table 2 flywheel material parameters
3 飞轮转子模型应力分析
由表1可知,两模型除了轮缘高度其他参数都相同。由理论力学可知,当模型二轮缘高度为模型一轮缘高度的两倍,且两飞轮模型以相同角速度绕中心旋转轴旋转时,两者转动惯量相等。将模型二轮缘高度乘0.5 得到模型二的折算轮缘高度,为了方便说明,之后也称轮缘高度。
由图3可知,轮缘的存在会使得飞轮厚度突变并必然导致应力集中。为了分析应力集中对飞轮整体应力的影响,通过逐步增大轮缘高度得到在不同轮缘高度下两种飞轮模型的最大径向、最大环向、最大轴向应力值与最大变形量。最大应力值可表征飞轮模型应对应力集中的能力,最大变形量则反映了飞轮模型应对变形的能力。两飞轮模型各项最大应力值随轮缘高度变化趋势见图5~7,比值为模型一应力值与模型二对应应力值之比。由图5 可知,随着轮缘高度的增加,模型一最大径向应力值单调增长,随后在轮缘高度为60 mm 时达到稳定值49.1 MPa;模型二最大径向应力值先增后减,分别在轮缘高度为10 mm 和30 mm 时达到最大值32 MPa 和极小值28.86 MPa,并在轮缘高度为60 mm时达到稳定值29.5 MPa。比值先减小并于轮缘高度为3.75 mm 时取得最小值0.698,随后增长至轮缘高度为60 mm时达到稳定值1.65,轮缘高度为17.5 mm时比值为1,此时两模型应力值相等。
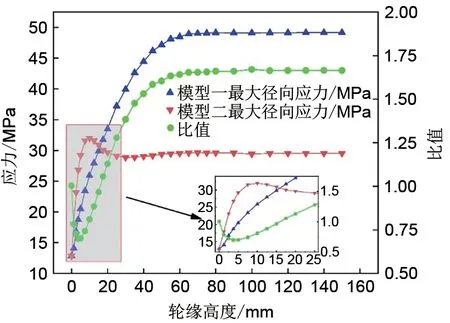
图5 飞轮模型的最大径向应力与应力比值Fig.5 Maximum radial stress and stress ratio of flywheel model
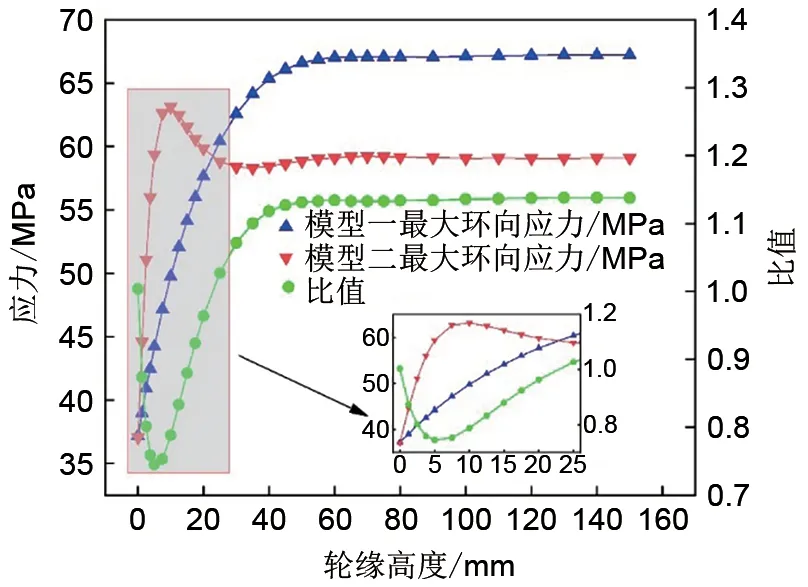
图6 飞轮模型的最大环向应力与应力比值Fig.6 Maximum circumferential stress and stress ratio of flywheel model
由图6可知,最大环向应力与最大径向应力变化趋势相似。随着轮缘高度增加,模型一最大环向应力值增大,并在轮缘高度为60 mm 时达到稳定值67 MPa;模型二最大环向应力值先增后减,最终在轮缘高度为60 mm 时达到稳定值59.1 MPa,其中最大值63.1 MPa 和极小值58.32 MPa 分别在轮缘高度为10 mm 和30 mm 时取得。比值在轮缘高度为3.75 mm 时取得最小值0.745,随后升高并在轮缘高度为22.55 mm 时达到1,最终在轮缘高度达到60 mm时达到稳定值1.133。

图7 飞轮模型的最大轴向应力与应力比值Fig.7 Maximum axial stress and stress ratio of flywheel model
如图7所示,两模型的最大轴向应力值相差较大,随着轮缘高度增加,模型一最大轴向应力明显增大,其稳定值47.5 MPa 出现在轮缘高度为80 mm时;模型二的最大轴向应力值在轮缘高度为10 mm 处取得最大值16.3 MPa,之后应力值随轮缘高度增加而减小,并在轮缘高度为60 mm时达到稳定值8.96 MPa。比值在轮缘高度为2.5 mm时取得最小值0.52,随后快速增长至5.3并达到稳定。
对于最大变形量,如图8所示,随着轮缘高度增加,模型一最大变形量不断增大但增速逐渐变缓,当轮缘高度为150 mm 时,最大变形量为50.447 μm;模型二最大变形量变化呈增-减-增趋势,在轮缘高度为10 mm 与45 mm 时分别取得极大值89.902 μm 与极小值68.471 μm,两种飞轮模型最大变形量最终都不断增大。应力比值分别于轮缘高度为7.5 mm和90 mm时取得极小值0.2254和极大值0.6077,且始终不大于1,表明模型二最大变形量始终大于模型一最大变形量。
由上述分析可得,在相同载荷和材料条件下,轮缘高度很小时,模型一应力性能略优于模型二,但轮缘高度较大时,模型二的应力性能远优于模型一。相对的,由于模型二的轮缘集中在一侧,使其最大变形量始终大于模型一的最大变形量,变形量比值还将随着轮缘高度增大而不断降低。并且注意到轮缘高度超过某一临界值后,两种飞轮的最大应力值都将达到稳定。
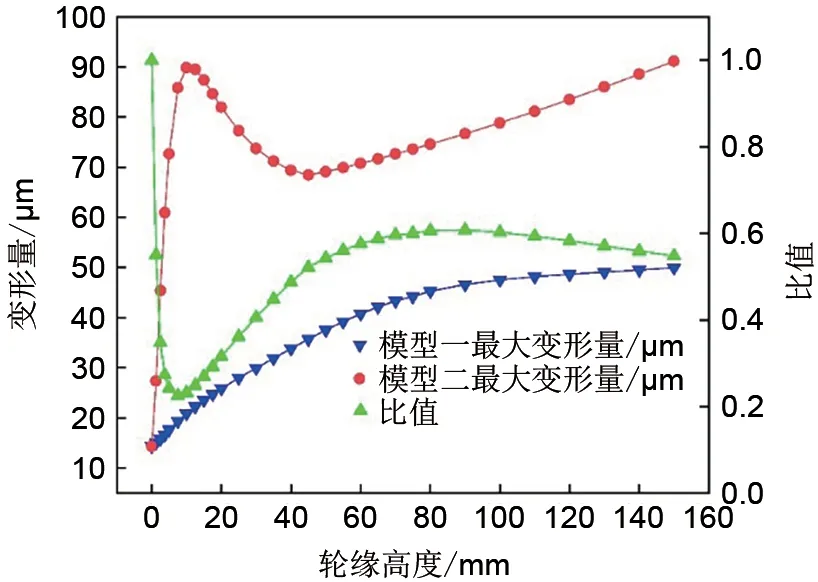
图8 飞轮模型的最大变形量与变形量比值Fig.8 Maximum deformation and deformation ratio of flywheel model
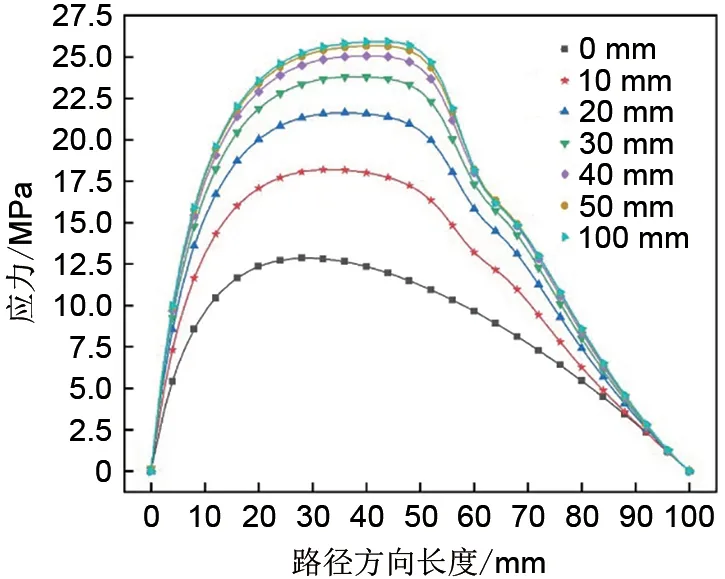
图9 模型一沿路径方向的径向应力分布Fig.9 Radial stress distribution along path of model 1

图10 模型二沿路径方向的径向应力分布Fig.10 Radial stress distribution along path of model 2
为了进一步研究在轮缘高度对应力在飞轮半径方向上变化的影响,结合在不同轮缘高度下飞轮模型最大应力值的变化情况,选取7个合适的轮缘高度值,分析两种飞轮模型的各项应力值在给定的轮缘高度下沿图3 中路径A-B 的变化情况。如图9 和图10 所示,两飞轮模型沿路径方向的径向应力都呈先增后减的趋势,并且在路径长度为0 mm 与100 mm,即飞轮模型的内径与外径处,径向应力值都接近0,这与式(2)相符。如图11和图12所示,径向应力最大值出现在飞轮内径,环向应力沿路径方向单调递减。如图13,路径长度小于40 mm时,模型一轴向应力接近0;路径长度为60 mm时,轴向应力取得最大值。由图14 可知,模型二轴向应力在路径长度小于35 mm 时接近0,路径长度为55 mm 时取得最大值,路径长度为70 mm 时取得负的极小值,代表此处取得反向的应力极值。由上述分析可知,随着轮缘高度的不断增大,径向应力与环向应力随之增大,但变化趋势没有发生明显改变,仅在厚度突变处(60 mm)应力曲线出现了略微的弯曲,代表此处应力降低速度变快;轴向应力受轮缘影响较大,应力曲线在轮缘附近出现显著的凸起,代表轴向应力在此处突增,说明在轮缘高度较大的情况下,飞轮转子不能简单地利用平面应力理论进行分析,否则可能会导致较大的误差。
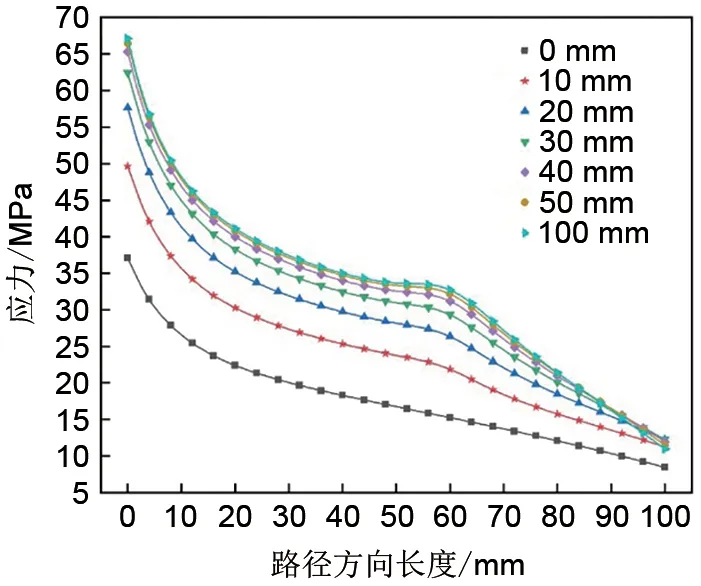
图11 模型一沿路径方向的环向应力分布Fig.11 Circumferential stress distribution along path of model 1
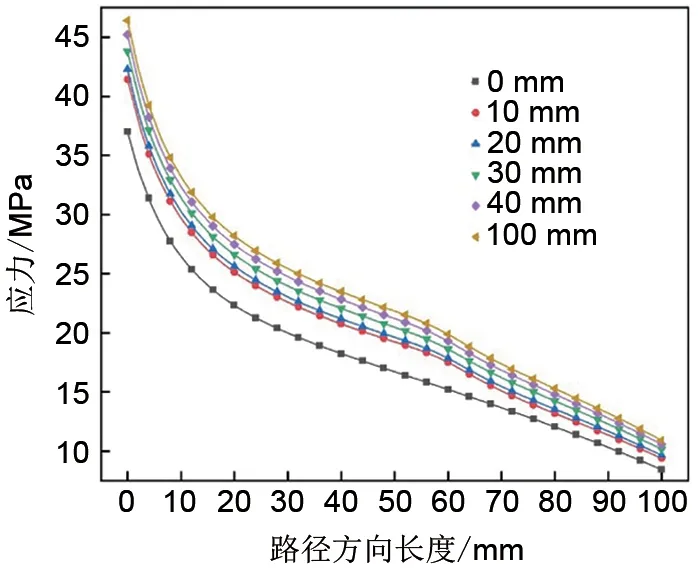
图12 模型二沿路径方向的环向应力分布Fig.12 Circumferential stress distribution along path of model 2

图13 模型一沿路径方向轴向应力分布Fig.13 Axial stress distribution along path of model 1
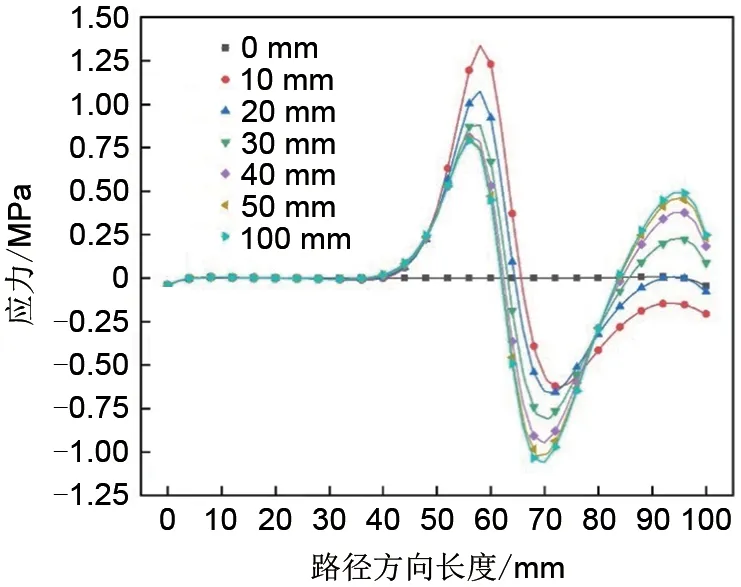
图14 模型二沿路径方向轴向应力分布Fig.14 Axial stress distribution along path of model 2
如图9~14 所示,轮缘高度达到50 mm 后,再增大轮缘高度对两种飞轮模型各项应力的影响变小,轮缘高度为50 mm和100 mm时的应力变化曲线几乎重合,这与飞轮整体最大应力相似,超过轮缘高度临界值后路径方向应力也达到稳定值。为进一步得出路径方向达到应力稳定时对应的临界轮缘高度,逐渐增大轮缘高度,得到不同轮缘高度下两种飞轮模型沿路径方向的各项最大应力值,如图15 所示,随着轮缘高度增加,模型一沿路径方向的最大径向、最大环向、最大轴向应力分别在轮缘高度为60、60、70 mm时达到稳定值25.9、67、12 MPa;模型二沿路径方向的最大径向、最大环向应力、最大轴向应力则分别在轮缘高度为60、60、40 mm 时达到稳定值16.7、46.3、0.8 MPa。通过上述分析可以得知,模型一沿路径的最大径向、最大环向、最大轴向应力稳定值比模型二对应应力稳定值分别大54.3%、44.4%和1420%。通过对比图15 与图5~7 可以发现,随着轮缘高度增大,无论是受应力集中影响较大的飞轮整体最大应力,还是受应力集中影响较小的沿路径方向的飞轮应力都最终达到稳定状态。
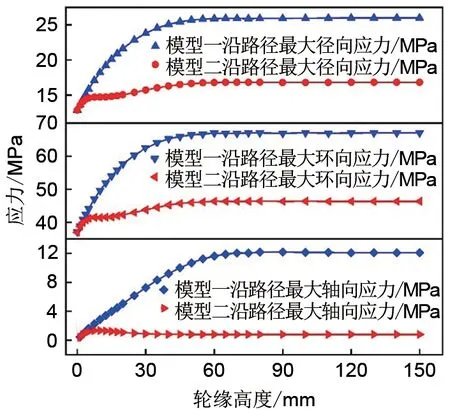
图15 飞轮模型沿路径的最大应力Fig.15 Maximum radial stress and stress ratio along path of flywheel model
4 结 论
(1)随着轮缘高度增大,飞轮模型一的最大应力值与沿路径的最大应力值都将上升;飞轮模型二的最大应力值与沿路径的最大轴向应力随着轮缘高度增加先增大后减小,而沿路径的最大径向、最大环向应力值单调增长。轮缘高度超过临界高度后,两种飞轮模型的各项应力值都将达到稳定值。在本文的飞轮转子模型和载荷条件下轮缘高度临界值约为60 mm,针对不同的飞轮转子模型需要根据实际情况确定轮缘高度临界值。
(2)在不同轮缘高度下两种飞轮模型沿路径方向的径向应力、环向应力变化曲线与理论情况相符,径向应力呈先增后减的趋势;环向应力单调减少,最大环向应力出现在飞轮内壁。需要注意的是,两种飞轮模型沿路径方向的轴向应力值在无轮缘部分都接近零,但是靠近有轮缘部分后轴向应力明显增大,并在厚度突变处附近取得最大轴向应力值,随后应力下降并反向,对于飞轮模型二,其轴向应力下降后还会再次上升回到正值。
(3)轮缘存在时飞轮应力不能完全视为平面应力,在工程设计中需要适当考虑轴向应力的影响,在本文中应力值稳定后,两个飞轮模型的轴向应力最大值分别为其环向应力最大值的70.3% 和15.16%,若忽略轴向应力则会造成较大的误差。
(4)稳定后,模型一的最大径向应力、环向应力、轴向应力比模型二对应应力分别大65%、13.3%、430%,沿路径的最大径向、环向、轴向应力稳定值比模型二对应应力分别大54.3%、44.4%、1420%,最大变形量比模型二的最大变形量小43.89%,这说明采用模型一在控制变形上更有优势,而采用模型二能更有效降低应力。
由上述结论可得,通过确定飞轮轮缘高度临界值后可以确定其应力稳定值。在相同的条件下,采用类似模型一的飞轮结构对材料性能要求更加严格,但采用高弹性模量材料满足应力要求时可以有效减小飞轮变形,降低飞轮变形造成安全事故的可能性;采用类似模型二的飞轮结构可以选用弹性模量较低的材料以降低制造成本,或者适当增加飞轮转速以提高飞轮储能量,但必须注意轮缘变形带来的影响。对于两种模型而言,轮缘高度超出临界高度后但变形量仍留有较大裕度的情况下,可以合理增加轮缘高度以提高转动惯量。

