砂土中水平条形锚板竖向拉拔承载力统一计算方法研究

姚 琛，胡 伟，孟建伟，雷 勇，曾 兴，郑恒良

(1. 湖南科技大学，岩土工程稳定控制与健康监测省重点实验室，湖南，湘潭 411201；2. 湖南科技大学土木工程学院，湖南，湘潭 411201；3. 中铁十二局集团第一工程有限公司，陕西，西安 710038)

锚板具有良好的抗拔承载性能，在基础工程、锚固与加固等工程中已有较为广泛的应用[1-3]。近年来在相关工程领域仍有持续报道，如韩启云等[4]，刘湘莅等[5]报道了锚板在河南膨胀土地区输电线塔基础和1100 kV 特高压直流输电线塔基础中的应用。谭红莹[6]，李书兆等[7]报道了锚板在水下生产系统防沉板基础方面的工程应用。竖向极限抗拔承载力是水平锚板工程设计时的重要指标，该指标主要受锚板埋深、尺寸和土体性质等因素的影响，相应规律即为锚板抗拔承载机理，是开展锚板极限抗拔承载力理论研究的前提，锚周土体滑动面的变化特征则是其主要方面[2,8]。有模型试验和数值模拟研究表明：水平锚板竖向极限拉拔时，锚周土体滑动面存在两种截然不同的形态，即浅埋时以直线或曲线形状延伸至地表，深埋时则呈“灯泡状”局限于土体内部，分别如图1(a)和图1(b)所示[9-11]。

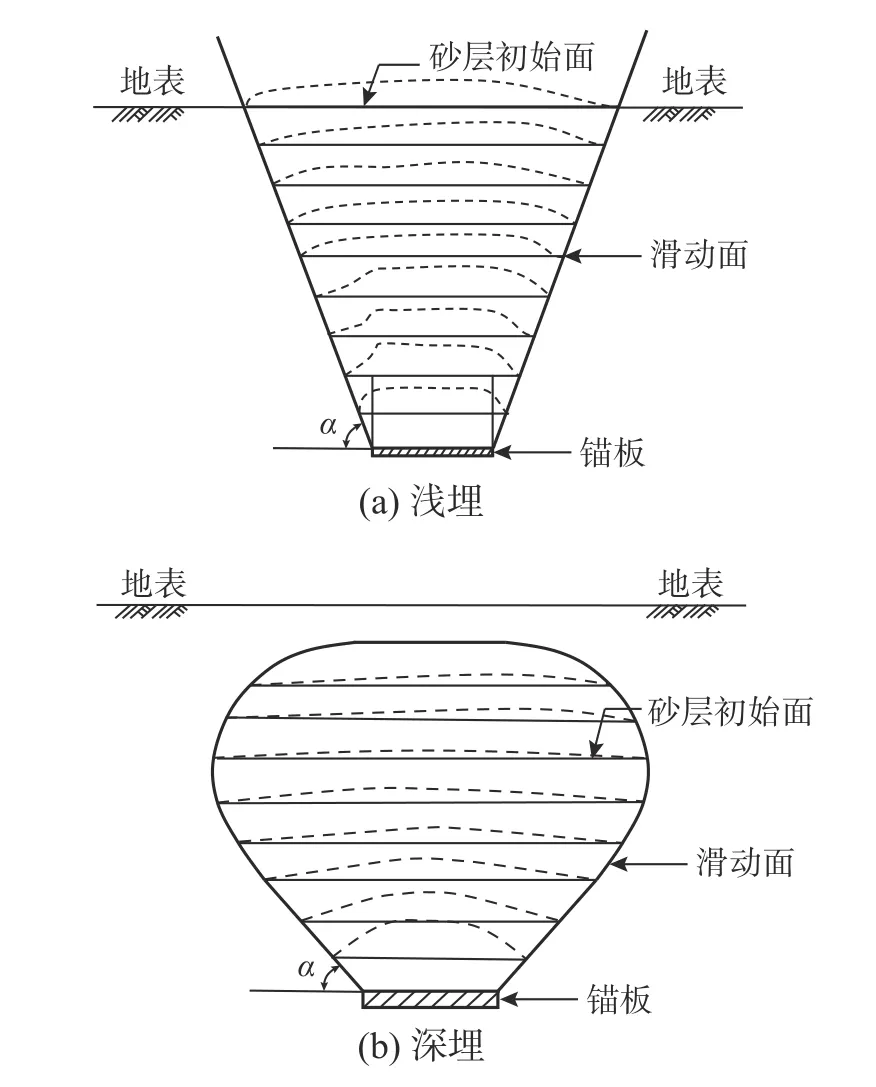
图 1 两种滑动面形态Fig. 1 Two types of sliding surface

基于这两种形态，理论研究中一般事先引入临界埋深比的概念来人为区分锚板类型，即浅埋和深埋，而后分别构建力学模型来推求极限承载力。因此，确定临界埋深比对现有承载力计算模型和方法至关重要。表1 中列举了砂土中锚板临界埋深比的部分研究成果，表中H/m 表示锚板埋置深度，即锚板上表面距地表的垂直高度，D/m为锚板宽度，H/D为锚板埋深比。临界埋深比一般与砂土的密实状态有关，但不同研究成果显示其大小差异显著，并无统一认识。这也就意味着，对于同一锚板工程，若设计者采用不同的临界埋深比取值标准，锚板将具有不同类型，相应的承载力计算模型、方法和结果将有明显不同，这对工程设计而言存在很大风险。故临界埋深比存在的意义，甚至其是否存在是值得商榷的。事实上，Ghaly 等[12]，朱长歧等[13]都在试验中发现，随着埋深比的增加，拉拔破坏由浅埋型向深埋型渐近转化，其间并没有明显的界限。因此，有必要重新审视以往区分浅埋和深埋的研究思路，而从统一的视角来看待锚板拉拔破坏机理从浅埋到深埋的连续变化。本文将针对水平条形锚板的竖向拉拔开展承载力计算的统一方法研究，尝试构建描述滑动面连续变化的统一形态函数和相应力学模型，推导拉拔承载力计算方法，并与其他试验、方法开展对比验证分析。

表 1 不同浅埋、深埋界定标准Table 1 Different definition standards

1 滑动面形态统一描述

水平锚板竖向极限拉拔时锚周土体滑动面具有浅埋时近似直线延伸至地表，埋深增大，滑动面逐渐内倾，至深埋时呈气球状闭合曲线形态局限于土体内部的连续演化规律[3]。若从统一视角审视锚板承载机理，最关键要理清滑动面这一渐变特征，构建能统一描述该变化规律的形态函数。对数螺旋线函数是常用于描述土体中滑动面的函数形式，本文的滑动面统一形态函数构建也以此类函数作为基础。基于相应的演化特征，滑动面形态函数需满足如下三个约束条件：

1) 锚板浅埋时，滑动面近似直线延伸至地表。对数螺旋线形态函数需满足当埋深比趋于0 时，其极径r0趋于无穷大。

2) 随着埋深比增加，滑动面曲线形态内倾并向锚板附近收缩。对数螺旋线形态函数极径r0是关于埋深比的减函数。埋深比趋于无穷大时，r0=D。

3) 滑动面曲线上任意一点的切线与水平向的夹角为α，该夹角在锚板边缘处初始值α0的大小与砂土的密实度有关。

为此，滑动面形态函数构建如下：

即滑动面是关于θ、φ、D和埋深比H/D的函数，式中：r0为初始极径；ρ 为极半径；φ为土体内摩擦角；θ 为对数螺旋线滑动面上一点对应的极角，其值在0～π/2 之间变化；a、b为常数。Ρ对于θ 角求导可得：

根据约束条件式(3)，将θ=0°代入式(2)～式(4)，再联立式(5)得到关于b的表达式如式(6)所示：

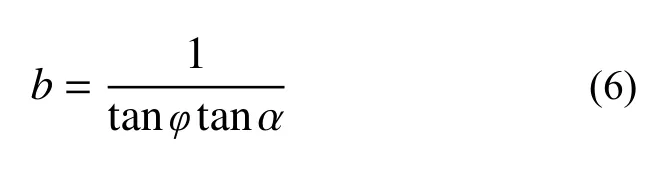
关于α0的取值，已有学者采用试验、数值模拟等方法开展了相关研究。对于浅埋工况，Ilamparuthi等[3]基于试验建议α0=π/2-φ/2。Liu 等[22]在试验中观测到倾角与砂土密实度相关，对于松砂，α0近似等于π/4+φ/2；对于密砂，α0则约等于π/2-φ/4。刘君等[23]采用颗粒流分析软件计算得到α0约等于π/2-φ/2。Murray 等[24]在极限平衡分析中采用α0=π/2-φ/2；在下限分析中则采用α0=π/2-φ。张昕等[2]的理论研究中采用α0=π/2-φ。深埋锚板的试验与理论研究相对较少，初晓锋等[15]在钙质砂中观测到α0介于π/2-φ/4 和π/2-φ/2 之间。Ilamparuthi 等[3]则观测到α0约为π/2-φ/2。综上，关于α0的取值，总结已有研究成果如表2 所示。

表 2 α0 取值Table 2 Values of α0

据上述总结分析，本文建议α0的取值规则如下：松砂取α0=π/2-φ/2；中密砂取α0=π/2-3φ/4；密砂取α0=π/2-φ。经计算总结，常数a的取值对于松砂、中密砂和密砂分别为0.01、0.02、0.03。

2 统一力学模型与理论推导

取地面、滑动面、锚板围成的空间体为隔离体，隔离体受力分析如图2 所示，受重力G，含隔离体内土体重力Gs和锚板重力GM，滑动面上所受土压力正应力合力E和相应的切应力合力f，竖向拉拔力F四个力的共同作用。

不同埋深下螺旋线滑动面最终都将与锚板中心竖直线所在直线相交，设该交点对应的θ 角与距锚板的距离分别为θmax和ymax(如图3)。在给定埋深H的情况下，θmax可由式(7)求取，ymax计算如式(8)所示。据滑动面形态函数可知，滑动面以锚板边缘为起点，在向锚板中心竖直线方位的延伸过程中，其上必然存在一点，该点的切线为竖向线，即斜率K为无穷大。该点对应的θ 角与距锚板的距离分别为θ1和y1(如图3)，则有0＜θ1＜θmax，0＜y1＜ymax。在给定埋深下，θ1可通过式(9)求取，y1的表达式如式(10)所示。

图 2 隔离体受力分析Fig. 2 Isolator force analysis

图 3 y1 和ymax 示意Fig. 3 Schematic of y1 and ymax

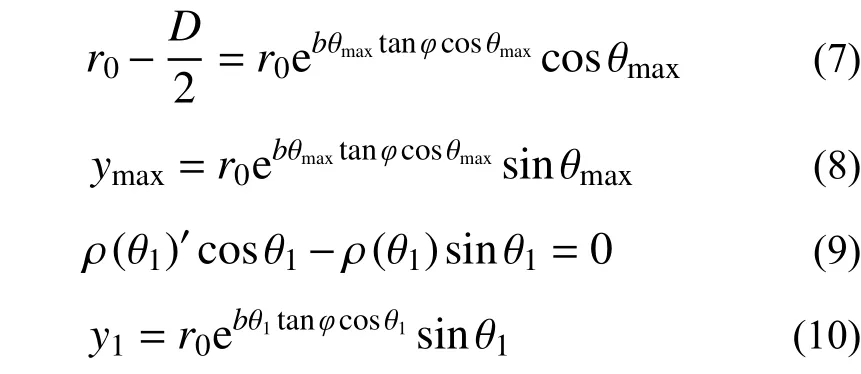
据埋深H、y1和ymax的大小关系，隔离体受力计算分为三种工况：①H＜y1；②y1≤H＜ymax；③ymax≤H。

1) 当H＜y1时，如图4 所示：地面位置低于临界点，滑动面能贯通至地表。滑动面和地表交点对应的θ 角为θ2，其值由式(11)求取。以锚板所在水平面直线为x轴，拉杆中心线向上为y轴正方向，两者交点为原点建立坐标系，沿y轴正方向坐标Y处取厚度为dy的微元，滑动面上正应力合力微元dE，切应力合力微元df分别如式(12)、式(13)所示。

式中：γ 为土体重度；K1是滑动面上与y1对应位置处的土压力系数。当ρsinθ=0 时，即锚板边缘处，因挤压土体程度最为强烈，假设该处法线方向作用被动土压力，即σp=Kpγh，h为计算点埋深，Kp为朗肯被动土压力系数，Kp=tan2(π/4+φ/2)；相应切线方向应力τf=σptanφ。当ρsinθ=y1时，即临界点位置处，因滑动面在此处沿竖向运动，故假定该点土压力系数采用静止土压力系数，K0=1-sinφ。其他位置时，土压力系数则随ρsinθ 发生变化，在Kp和K0之间进行线性插值计算，如式(14)。

图 4 H＜y1 的滑动面Fig. 4 Sliding surface of H＜y1

滑动面上力学分析如图5 所示，积分可得滑动面所受正应力合力和摩擦力合力的竖向分量，如式(15)和式(16)。该工况下滑动面所受正应力合力的竖向分量方向向上，λ 由式(4)求取。

图 5 滑动面上力学分析Fig. 5 Mechanical analysis of sliding surface

对于工况②和工况③，其理论推导过程与工况①类似，限于篇幅，仅给出E2、f2、Gs2、E3、f3、Gs3的计算表达式，将其代入式(18)即可得到相应的极限拉拔承载力。对于工况②，以临界点为分界，临界点以下，滑动面上土压力系数K1由式(14)计算；临界点以上，土压力系数K2介于临界点静止土压力系数K0和1 之间，根据点到锚板的距离按线性插值进行计算。若锚板位于地下水位以下，则地下水位以下部分的荷载计算使用有效重度进行。

3 对比验证

3.1 统一性验证

根据文献[24]中的试验数据，绘制埋深比1、5 和8 三种工况的滑动面如图6 所示。

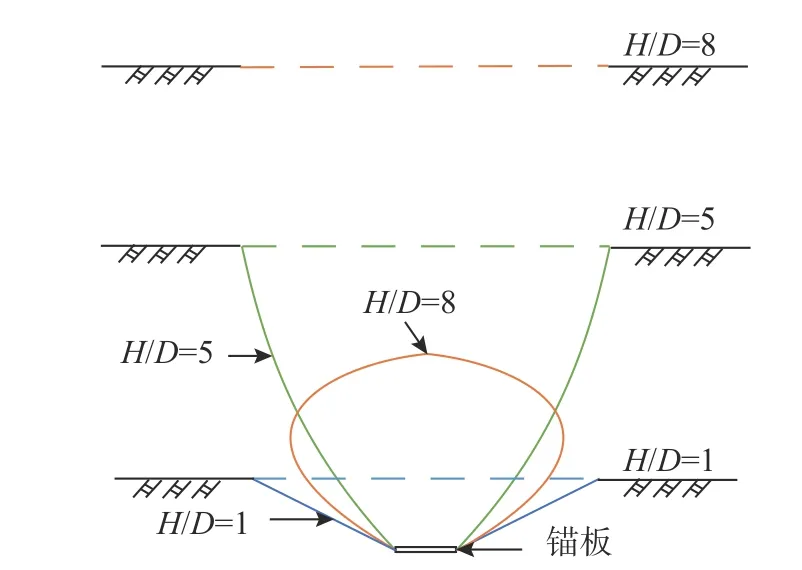
图 6 计算滑动面演化Fig. 6 Evolution of calculated sliding surface

在埋深比较小时，如图中H/D=1 工况所示，滑动面近似直线延伸至地表；随着埋深比的增大，如图中工况H/D=5 所示，滑动面向锚板中心线方向内倾，呈现曲线形态，意味着锚板承载模式由浅埋向深埋过渡；埋深比进一步增大，滑动面则不再延伸至地表，而呈现闭合“球泡”状全部局限于土体内部，此时可视为深埋模式，如图中工况H/D=8 所示。由此可见，本文统一法所构建的形态函数能很好地再现滑动面随埋深比的连续演化过程，实现了一个力学模型可反映不同埋深比下拉拔破坏机理的连续变化，无需再人为区分浅埋、深埋。

3.2 承载力计算对比

选用9 种计算方法，分别是Meyerhof 等[25]所建立的上、下限法，简称方法1、方法2；Murray 等[24]方法，简称方法3；Frydman 等[26]方法，简称方法4；Cheuk 等[27]方法，简称方法5；Deshmukh 等[28]方法，简称方法6；张昕等[2]方法，简称方法7；黄明华等[29]方法，简称方法8；本文方法，简称统一法。方法5 和方法7 中剪胀角 ψ的计算按文中采用式(26)进行[17,19]，对于石英砂，Q可取10，p'为锚板埋深处的自重应力。

1)案例介绍

本文选取的5 个试验案例包括：Rowe 等[30]试验(试验1)、丁佩民等[16])松砂试验(试验2)、丁佩民等[16])密砂试验(试验3)、Dickin[31]松砂试验(试验4)、Dickin[31]密砂试验(试验5)。5 个试验案例均采用砂土，内摩擦角φ在32°～45°变化，密实度Dr大小则表明试验涵盖松砂(23%、33%)和密砂(87%、76%)两种状态。锚板长宽比(L/D)在6.0～8.7，满足条形锚板对L/D＞5 的要求[24,30]；埋深比均包含1～8，共八种工况，具体情况如表3 所示。

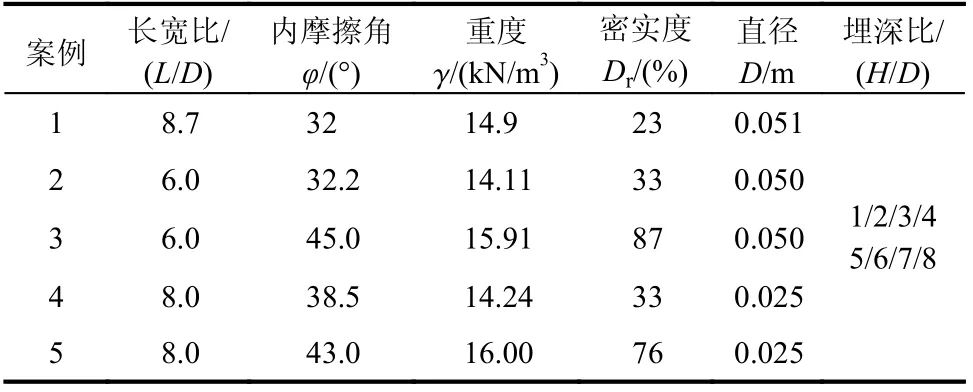
表 3 五个试验案例基本情况Table 3 Basic information of five tests

2)结果对比分析

分别采用上述9 种方法对上述5 个试验案例进行计算，并与实测值进行对比；计算每种方法对于各案例工况的计算值与实测值之比，并取比值的平均值x和相应标准偏差σ 作为评价上述计算方法适应性的指标。

a) 试验1

实测值与计算值的对比如图7 所示，除方法七计算值整体上只有约实测值的1/3，严重偏小以及方法八计算值整体是实测值的1.6 倍，严重偏大外，其他7 种方法对此试验工况均表现出较好的适宜性。具体而言，方法2、方法4 和方法6 计算值均与实测值非常接近，比值均值分别是0.93、1.03 和1.05，意味着计算值和实测值的误差在10%以内，且随着埋深比增加，比值趋势很稳定，标准偏差分别是0.1、0.1 和0.08，计算效果非常理想。方法1 和统一法计算效果处于第二梯队，计算值和实测值的误差在15%以内，比值均值分别为1.12 和0.87，即方法1 计算值总体偏大，而统一法总体偏小，但后者比值的标准偏差要比前者大。第三梯队为方法3、方法5，计算值误差均在30%左右，方法3 计算值偏大，而后者则偏小。因此，对于试验1，方法4 计算效果排名第一，统一法排名第五，方法7 计算效果最差。

图 7 试验1 结果与计算值对比Fig. 7 Test values versus calculated ones of test 1

b) 试验2

实测值与计算值的对比如图8 所示。在埋深比小于等于5 时，各方法的计算值随埋深比的增加而增大，且增幅较小；而在埋深比大于5 后，计算比值增长呈迅速增大趋势，其原因在于实测值此时已基本保持不变，而计算值仍在持续增大。这说明所有方法均无法反映该试验埋深比大于5 后承载力趋于稳定的现象，故剔除掉埋深比为6、7 和8 的数据点，仅对埋深比小于等于5 的工况进行对比。经过计算，方法5 计算效果最好，计算值与实测值的误差为3%，方法2 与统一法计算效果次之，误差分别为16%和28%。方法8计算值严重偏大，比值均值2.51 最大，方法7 则相反，比值均值0.76 最小，其他方法的计算效果则介于这两者之间。标准偏差方面，方法1 标准偏差为0.26，离散性最小，统一法排名第二；方法8 标准偏差数值达到1.2，离散性最大。因此在埋深比小于等于5 时，方法5 效果最好，方法1次之，统一法排名第3，方法8 效果最差。若考虑所有埋深工况，方法7 比值均值1.39 为最小，计算值偏大，标准偏差为39%，离散性排名第3。方法5 比值均值排名第2，但离散性优于方法5 排名第1。方法8 计算值最大，比值均值为4.04，离散性同样为最大。因此，从整个试验来看，方法7效果最好，方法5 次之，统一法排名第3，方法8计算效果最差。

图 8 试验2 结果与计算值对比Fig. 8 Test values versus calculated ones of test 2

c) 试验3

由图9 可以明显看出，埋深比小于3 时，所有方法的计算值均小于实测值。埋深比大于等于3 后，计算比值的趋势则较为稳定。暂不考虑埋深比1 和2 的工况进行分析。经过计算，方法3 比值均值最大，为1.62，方法5 比值均值最小，为0.43。方法2 计算效果最好，计算值与实测值误差为2%，方法6 次之，误差为6%，方法4 排名第3，统一法排名第4。从总体来看，方法1 和方法6 的比值均值分别是1.04 和0.9，意味着计算值和实测值的误差在10%以内，标准偏差分别是0.04 和0.1。计算效果第二梯队是方法2 和统一法，比值均值分别为0.83 和0.8。两种方法相比，虽然统一法计算值略微偏小，但从整体上来看，在埋深比大于3 之后，计算值增长趋势更稳定且非常接近于实测值，而方法2 计算值则持续增大，比值最大达到2 左右。方法3、方法4、方法5、方法7和方法8 计算效果处于第三梯队，比值均值分别为0.34、0.22、0.62、0.45 和0.61，这五种方法的计算值与实测值的误差在22%～62%。从计算结果的离散程度来看，方法8 的比值均值标准偏差0.72 是最大的；统一法离散性最小，标准偏差为0.18，但其比值均值排名4。总体而言，方法1 计算值最接近实测值，计算效果最好。方法8 无论是从比值均值还是标准偏差来看，效果均为最差。

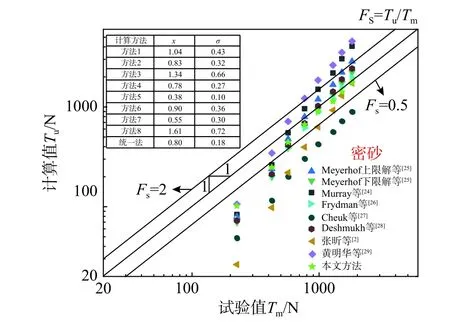
图 9 试验3 结果与计算值对比Fig. 9 Test values versus calculated ones of test 3

d) 试验4

如图10 所示，整体上看，当埋深比小于等于6 时，各方法计算值与实测值的比值较为稳定，其中方法7 的比值大都小于0.5，计算值整体偏小；方法8 的比值均大于2，计算值整体偏大，其他方法的比值则在0.5～2.0。当埋深比大于6 以后，各方法的计算比值均陡然增大，其原因在于实测值此时已基本保持不变，而计算值仍在继续增大。这说明所有方法均无法反映埋深比大于6 后承载力趋于稳定的试验现象，故先剔除掉埋深比为7 和8 的数据点，仅对埋深比小于等于6 的工况进行对比。经过计算，统一法比值均值为0.94，与实测值最接近，方法2 和方法4 分别为1.13 和1.15，计算误差在15%以内；方法5 和方法6 分别为0.73 和1.25，计算误差在25%左右；方法8最大，为1.99，方法7 则最小，为0.48。标准偏差方面，方法2 和方法6 在0.09 左右，离散程度较小；方法8 和统一法则在0.25 左右，离散性偏大。因此，对于埋深比小于等于6 的工况，方法2效果最好，统一法次之，方法8 效果最差。如若考虑所有埋深情况，统一法比值均值为1.02，计算值与实测值最为接近，误差仅为2%，但标准偏差为0.3，要大于方法5 的0.17 和方法4 的0.26，排名第三。方法2、方法4 和方法5 的比值均值分别为1.3、1.27 和0.8，三者的计算误差在20%～30%，前两者的计算值偏大，方法5 的计算值则偏小。方法8 的比值均值和标准偏差分别为2.41 和0.84，均为最大值，其计算效果仍然为最差。

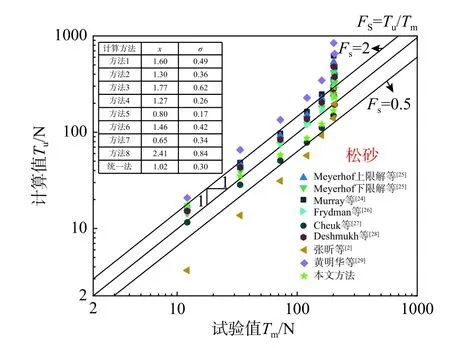
图 10 试验4 结果与计算值对比Fig. 10 Test values versus calculated ones of test 4

e) 试验5

如图11 所示，与前四个试验案例相比，各方法对该试验的计算比值随埋深比的增长趋势都较为平稳，总体效果均表现较好。方法四比值均值为1.02，计算值与实测值误差仅为2%，标准偏差为0.09，计算效果与离散性均为最好。方法1、方法2、方法3、方法6 和统一法的计算效果位于第二梯队。从比值均值来看，方法6 排名第2，统一法排名第3；从离散程度来看，方法6 优于统一法。方法3 在埋深比大于3 后，计算值增长较快，比值均值为1.24，整体偏大，而方法1 与方法2 的计算值则整体偏小，三者计算值与实测值的误差分别为24%、21%和35%。方法5、方法7和方法8 的计算效果位于第三梯队，比值均值分别为0.43、0.47 和1.67，说明方法8 计算值整体偏大，方法5 和方法7 则整体偏小，三者计算比值的离散程度均较小，标准偏差分别为0.12、0.11 和0.13。

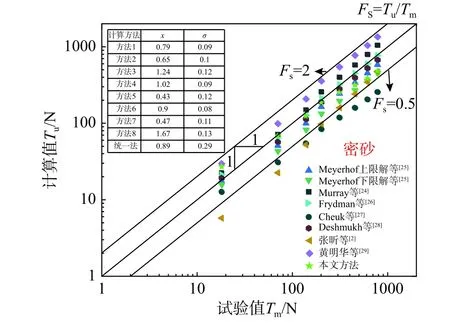
图 11 试验五结果与计算值对比Fig. 11 Test values versus calculated ones of test 5

上述9 种方法对五个试验案例的计算效果排名汇总如表4 所示。方法4 在试验1 和试验5 两个案例的计算中效果最佳，方法1、方法7 和统一法则分别在试验3、试验2 和试验4 一个案例的计算中效果排名第一，但与方法1 和统一法相比，方法7 同时还在一个试验案例计算中效果最差，在两个试验案例中效果排名倒数第二，计算效果较不稳定。另外，还值得注意的是，方法6 在三个试验案例的计算中效果排名第二，计算效果较好且表现稳定。方法8 在两个试验案例计算中效果最差，还在另两个试验案例计算中效果排名倒数第二，总体上表现最差。以各方法计算效果排名数字之和来衡量该方法的适应性，则方法6 得分15 分最低，表明其适应性最好；其次是统一法，得分为16 分；方法8 得分为41 分，适应性最差。

表 4 计算效果对比分析Table 4 Comparative analysis of calculation effect

4 结论

通过深入分析总结砂土中水平条形锚板竖向拉拔承载机理，提出了描述滑动面随埋深比连续变化的形态函数，建立了无需区分浅埋、深埋的极限拉拔统一力学模型，并建立了水平条形锚板竖向拉拔极限承载力的统一计算方法。与其他计算方法和试验案例的对比分析很好地验证了本文力学模型的统一性和统一计算方法对于砂土中水平条形锚板竖向拉拔承载的适应性。主要结论如下：

(1) 以对数螺旋线函数为基本形式，构建了可反映滑动面随埋深比连续变化的形态函数，并根据约束条件和以往研究成果确定了其中参数的计算公式和取值。

(2) 根据埋深大小、滑动面交点与锚板距离以及滑动面上竖向线切线对应点与锚板距离这三者的大小关系，分3 种情况进行极限平衡分析，建立力学平衡方程，建立了砂土中水平条形锚板竖向拉拔极限承载力统一计算方法。

(3) 所形态函数很好地反映了滑动面随埋深比的连续演化过程，统一力学模型可反映不同埋深比下拉拔破坏机制的连续变化，无需再人为区分浅埋、深埋。在对五个试验案例(松砂、密砂)的计算对比中，统一法在9 种方法中计算效果得分排名第二，表现出较强的适应性。