基于卷积长短期记忆网络的加热炉温度场实时预测方法

李 涛，王艳丽

(中国石油化工股份有限公司天津分公司，天津 300271)

加热炉是炼化装置的重要设备，若其燃烧过程不稳定，在运行过程中，可能会在随机位置出现局部超温。针对易结焦工艺介质，若加热炉的某局部位置长时间运行在超温状态，会导致炉管破坏失效，因此必须采取措施优化加热炉的燃烧状况【1】。但加热炉设备庞大、环境恶劣，难以对有关物理量参数进行在线测量，导致燃烧调整得不到可靠的依据，难以实现燃烧优化运行。因此可以采取软测量的方案以获得工业加热炉温度场。

软测量指的是在工业生产中通过已经得到的测量值，结合计算机等应用技术，对难以测量和不能测量的变量进行数学推断，从而得到不能直接测量的重要变量的值。软测量具有动态响应迅速的优势，可以连续给出工业过程中的重要变量的值。

软测量模型可以划分为基于原理的软测量模型(Model-Driven Models，简称MDM)以及基于数据的软测量模型(Data-Driven Models，简称DDM【2】，又称为数据驱动的软测量模型)。

其中MDM用于工业过程中所涉及的复杂物理化学等有关理论知识，原理模型通常数值计算精度较高、可解释性强。但是基于机理的传统模型往往由大量代数方程组组成，计算量大、收敛慢，难以满足软测量实时性的要求。CFD是计算流体力学(Computational Fluid Dynamics)的缩写，也是MDM的一种。它利用数值分析的方法，可解决燃烧及流体流动的问题。加热炉温度、流量等工况数据可以作为CFD计算的依据，据此可以得到加热炉内部的温度计算值。CFD虽然可以计算出十分详尽丰富的工业加热炉三维温度场数据，但同样存在计算量大的问题，在现有计算能力下，难以获得实时温度场。

本文采用的基于深度学习的软测量建模方法属于DDM，作为一种基于数据驱动的模型，该方法的精度依赖于数据的数量以及准确性，在有充足数据支持的情况下，才可以得到满足需求的结果。

因此，提出了一种卷积长短期记忆网络的新方法，以CFD的高精度计算结果作为数据集，并且针对三维温度场使用卷积LSTM的网络结构进行训练，以实现对加热炉的温度场进行预测。

1 温度场预测实验

1.1 CFD模拟情况小结

在数值模拟中，本研究建立了符合实际情况的湍流模型和组分模型，并且据此生成了充足的网格进行计算，得到了加热炉内温度场的三维空间分布。计算模型是焦化炉F102B东室的二分之一，经热电偶数据修正后，扩展为整个F102B东室的炉膛三维温度场。将数值计算的结果与管壁上8个热电偶的温度进行对比，发现CFD仿真计算得出的温度场与8个管壁热电偶测得的温度误差都在5%以内。因此，可以认为CFD仿真得到的加热炉三维温度场能够很好地代表真实温度场。

1.2 实验数据集的建立

1.2.1 数据集的组成

本研究的目标是输入工况时间序列数据得到预测温度场。用于温度场预测的训练数据集分为输入的工况数据和仿真计算温度场数据两部分。工况部分是训练和测试时网络的输入数据。通过数据扩充CFD仿真计算得到的温度场数据是网络输出的真值。通过计算网络输出与真值之间误差的梯度，可以对网络参数进行优化，使得网络输出在下一次迭代中更加接近真值【3】。

1.2.2 典型工况的选取

工况部分由工业加热炉中分布式控制系统DCS的各个温度、压力、氧含量、空气流量等传感器间隔固定时间测量得到的19个变量组成。数据时间段为2018年。因为加热炉的温度变化相对缓慢，所以本研究采用的数据间隔为1 h，数据集中总共包括连续5835 h的数据。因为工况数据中每个变量的数值范围都不一样，实验中不同变量都被分别归一化到了[0,1]。

同时由于加热炉温度场具有一定的稳定性，工况没有较大改变的时间段内，温度场会在一个相对稳定的范围内波动，因此本研究根据管壁热电偶温度数据将5 835 h的工况划分为7个典型工况，以此来减少CFD计算次数。

1.2.3 基于典型工况的温度场数据

通过CFD计算得到了对应7个典型工况，每个典型工况为一组，包含5个温度场，共35个温度场。每个温度场都包含了工业加热炉内炉管管壁上的500 185个节点的温度值，如图1所示。但这样的数据结构并不适合作为网络的输出，因此将这些节点重新排列成一个14×32×652的矩阵。除此之外，温度场数据同样需要归一化到[0,1]，如图2所示。

图1 管壁温度场示意

图2 管道展开为矩阵示意

1.2.4 数据扩充

因为降阶模型需要大量的数据对网络进行训练，所以为降阶模型的训练能顺利进行，本研究根据实际情况构造出一系列的模拟温度场作为网络训练的数据使用。

本研究选取每个计算温度场对应工况附近的30个工况来构造模拟温度场。以模型输入量中各个管壁热电偶的温度为参照对CFD计算温度场进行调整，得到模拟温度场。

1.3 实验选用网络结构

本研究中的温度场预测是基于工况序列进行的，选用具有优秀时空序列建模能力的ConvLSTM网络进行预测。

本研究所设计的网络结构如图3所示。所述的温度场实时预测网络由编码网络(Encoding Network)和预测网络(Forecasting Network)部分组成，图3中的数字代表特征通道数;每一层的卷积核大小都为3×3，共有4层卷积长短期记忆网络(ConvLSTM)；输入(input)数据通道数为18，第一层长短期记忆网络(ConvLSTM 1)输出数据通道数为24，第二层长短期记忆网络(ConvLSTM2)输出数据通道数为48，第三层长短期记忆网络(ConvLSTM3)输出数据通道数为24；将第一层长短期记忆网络(ConvLSTM1)和第三层长短期记忆网络(ConvLSTM3)的输出数据进行拼接，得到通道数量为48的数据，并送入第四层长短期记忆网络(ConvLSTM4)，最终得到24通道的温度场输出(output)。由于网络是通过多个ConvLSTM层堆叠构成，所以它对于复杂动态系统的特征提取能力很强。

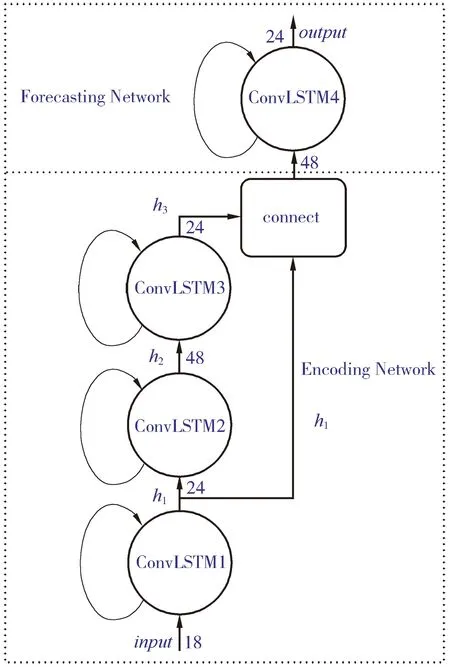
图3 网络结构

同时，第一层长短期记忆网络(ConvLSTM1)、第二层长短期记忆网络(ConvLSTM2)、第三层长短期记忆网络(ConvLSTM3)的输入和输出的时间序列长度均为10，第四层长短期记忆网络(ConvLSTM4)的输入时间序列长度为10、输出时间序列为长度3(h1～h3代表第1层～第三层长短期记忆网络的输出结果)。

1.4 网络训练

1) 对工业加热炉各数据采用式(1)分别进行归一化处理：

(1)

其中，x为要进行归一化的数据，mean、max、min分别为该工况数据训练样本范围内的均值、最大值、最小值；

2) 实际工况只是一维向量，与目标网络输出三维温度场并不匹配，因此需将一维的工况扩展成三维，即需要对工业加热炉各数据进行三维扩展。这里所述的数据包括按设定时间测量得到的工业加热炉中分布式控制系统的各个温度、压力、氧含量、空气流量的值；这里所述的扩展方法相同，均是将1个工况数据扩展成一个32×652的矩阵，矩阵中每个元素都填上该工况数据；而对于管壁上的8个热电偶的温度数据，扩展的时候只在热电偶对应的空间位置附近50个元素填上该热电偶测得的温度数据，其余元素置零，最后得到18×32×652的输入数据。

3) 将管壁温度场转换为三维温度场。因为三维温度场还包含了管壁的结构信息，但这样的温度场无法作为网络输出，因此本文将管壁温度场上的计算点重新排列成三维温度场。首先沿z轴将管道分为24根，然后将管壁沿轴切开展开成一个矩形，展开方法为按管道轴心方向依次选取32个点，并将32个点沿z轴方向进行排列，得到第一列数据；再沿管道轴心方向依次选取32个点继续排列，重复652次，得到一个24×32×652的矩阵；同时，将温度场的温度数值均除以1000，使其位于0～1之间，保留三维温度场每个点对应的管壁温度场的空间坐标。

4) 对温度场实时预测网络进行训练。训练时不冻结网络参数。训练时的初始学习率为0.01、批次大小为1，选择L1损失函数并采用Adam 算法进行优化。总共迭代600次，每迭代40次就将学习率乘以0.8进行衰减；网络在第480次迭代时达到最佳效果，得到最优模型；最优模型输出的平均绝对误差为28.3 K(开尔文)。

2 实验结果与分析

2.1 温度验证

由于经过CFD计算得出的温度场只有一个时刻的数据，而网络训练需要大量的数据，因此为使本实例能顺利进行，根据实际情况构造出一系列的模拟温度场作为网络训练的数据使用。

本文选取每个计算温度场对应工况附近的30个工况来构造模拟温度场。以工况中单个管壁热电偶的温度为标准对计算温度场进行调整，得到模拟温度场。例如对于15号工况的计算温度场，如果想要获得10号工况的模拟温度场，应当先计算10号工况中8个热电偶数据相对于15号工况中8个热电偶的变化百分比；然后根据8个变化百分比调整15号工况计算温度场对应管道的温度，而对于中间没有热电偶的管道则根据最近的两个热电偶的变化百分比采取渐变处理。

本次实验的温度场预测实际上是一个回归任务，对于此问题，本研究将使用平均绝对误差MAE来评价算法性能。MAE的计算见式(2)：

(2)

由上述结果可以看出，预测结果整体上的误差在可接受范围内。但也需要衡量局部的误差才能更好地反映算法性能。表1所示为针对第4 805 h的预测温度场和对应的8个热电偶的温度差。

表1 ConvLSTM预测在8个测点的温度对比

从表1可以看出：网络预测结果在局部细节方面也能很好地符合真实数据。

2.2 趋势验证

除了要求预测温度场符合真实工况外，还希望预测结果能够符合温度的变化趋势。图4～图11所示为8个热电偶在4805号工况以及往后20 h的真实值和预测值变化趋势对比。

图4 1号热电偶趋势

图5 2号热电偶趋势

图6 3号热电偶趋势

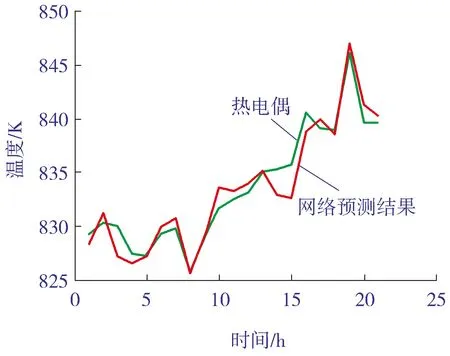
图7 4号热电偶趋势

图8 5号热电偶趋势

图9 6号热电偶趋势

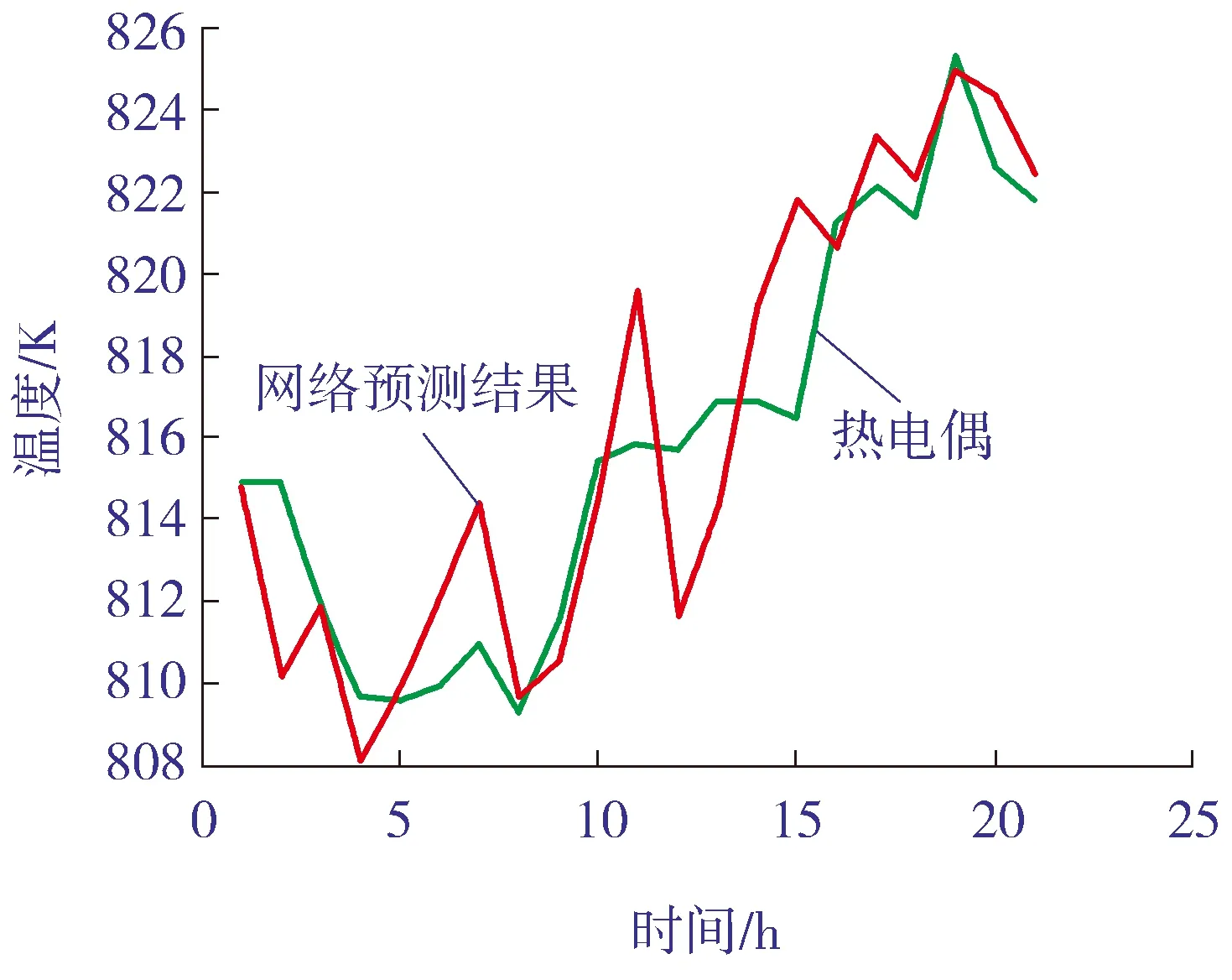
图10 7号热电偶趋势

图11 8号热电偶趋势

由图4～图11可以看出：网络的预测结果可以比较准确地预测工况的变化趋势。

2.3 温度场还原

在数据预处理阶段，本文将温度场重新排列为24×32×652的矩阵，便于网络输入与输出。在最后一步还需将矩阵还原为管壁温度场，这样可以更为直观地感受实验结果。图12和图13所示为4805号工况的计算温度场与预测温度场在matlab的三维散点建模结果，其中管道的缺口是由于计算点分布不均导致的在还原过程中缺少的相应计算点。

从图12和图13所示的还原建模图可以看出：网络的预测温度场与计算温度场十分相似，预测结果较好。

图12 计算温度场建模

图13 预测温度场建模

3 结论

对于加热炉内管道三维温度场进行预测是一个十分具有挑战性的问题，为了解决这一问题，提出了基于ConvLSTM的温度场预测算法。该方法以ConvLSTM为基础，通过合理的数据处理以及数据的跨层连接实现良好的温度场预测。

本研究利用CFD仿真计算得出的温度场以及由DCS记录的工况数据作为数据集，在设计的ConvLSTM网络中进行训练。从测试结果可以看出，无论是对于2018年的老数据还是2019年的新数据，网络预测结果与真实值的误差都在5%以内，并且网络预测结果也可以很好地跟上温度场随着时间变化的趋势，表明了本文的算法可以得到符合真实情况的预测温度场，而且能比较准确地预测出工况的变化趋势。在未来的工作中，将尝试引入更多的真实数据集进行训练，使得模型结果更为真实，同时也将继续改进该算法，以适应更加复杂的工况。