高效共享系统内存文件缺陷定位算法
于 娟
(仰恩大学 工程技术学院,福建 泉州362014)
0 引言
科技的发展对共享内存有了强烈的需求.共享内存系统由三部分组成[1],包括文件系统的接口、管理访问对象的软件集合以及对象属性.该系统在多处理器的计算机系统中,可以实现多个不同访问对象的访问.服务端用户借用内存管理子系统,高速共享缓存单元存放的文件,实现对访问用户的数据共享[2].但该系统在长期使用下,暴露出了部分缺陷,传统的定位算法通过设置监测节点,对该系统实时监测,当系统出现缺陷时发出警报,管理人员通过警报提示找出警报节点,对该节点的邻域进行缺陷排查,该方法固
然具有实时性特点,但得到的缺陷定位结果只有一个点位,所定位缺陷边界坐标的偏离系数过大,因此对排查造成一定程度的困难.针对传统方法的这一问题,提出无需二次排查的高效共享系统内存文件缺陷定位算法,该算法通过目标范围获取缺陷中心,进而得到更加明确的缺陷边界.该算法的提出不仅将缺陷具体到最远边线,实现全方位的缺陷定位,还在根本上降低了缺陷定位误差,解决了传统算法的现存问题.该算法为共享文件系统的缺陷定位提供了科学的技术手段,同时也为其他系统的缺陷定位提出严谨的设计思路.
1 高效共享系统内存文件缺陷定位算法
系统缺陷定位算法[3],第一步需要明确高效共享系统内存文件的功能特性,根据该系统运行的基本特征量,展开缺陷定位.该系统的文件共享模块与多个I/O端口连接,同时通过大量系统硬件执行共享指令,分析可知,该系统在各个连接结点和处理模块中,均可能发生缺陷,以此系统特征为基础,提出一个详细的缺陷定位算法.
1.1界定缺陷目标范围根据共享系统内存文件特性,利用CS技术设置搜索程序,界定缺陷位置的目标范围[4].预先计算步长因子,该因子是控制搜索区域广度的关键参数,当步长因子偏大时,控制该搜索程序展开全区域性搜索;步长因子偏小时,则该参数可以控制搜索程序,在局部区域展开局部搜索.为了控制该搜索程序在全区域、局部区域中的搜索平衡,加入平衡适应调节参数,令搜索程序分布式同步搜索.该步长因子的计算公式为:

公式(1)中:ls表示第s次的搜索步长,其中,s表示当前次数;lmax表示步长因子的最大上限;lmin表示步长因子的最小下限;ε表示引入的调节参数;N表示最大迭代总数;g1表示初始适应度下的最优函数;g2表示适合此次迭代的最优函数.同时,在该参数的搜索控制下,计算发现系统缺陷大致位置的发现概率,在CS技术中,一般情况下的发现概率取值在0.2~0.3之间,设置该参数下的概率为p,当该概率一直处于较大数值时,可以加快缺陷搜索的收敛速度;当发现概率p的值较小时,则此时的收敛速度降低,因此依靠最优适应度和前代解的比值设置最优适应度:

公式(2)中:fi表示上一代的最优适应度;fli表示在ls作用下的第i个解的适应度.根据上述计算公式,对发现概率适应度自由调节,得到的发现概率计算结果,如下所示:

公式(3)中:p′表示迭代后解的优质概率;di表示对第i个解的最优适应度;M表示解的总数量;pmin与pmax分别表示发现概率的上下限.综合上述两组公式得出搜索程序,对共享系统内存文件实施缺陷搜索指令,获取到的缺陷大致区域范围如图1所示.
图1中的搜索结果是缺陷目标范围,但此时该目标范围内不仅包含缺陷节点[5],同样包含少量正常节点,因此需要将缺陷节点从该范围中作出筛选操作.
1.2提取缺陷节点 利用捕获函数提取界定目标范围内的缺陷节点[6],该函数可以根据数据的载波频率,得到缺陷数据的码相位,实现对任意区域内数据节点的捕获.该捕获函数的捕获次数计算表达式为:

公式(4)中:n表示捕获次数;e1表示编码相位历遍次数;e0表示波频总步长;d表示缺陷数据波频步长;j表示固定常量,通常情况下为1.根据该捕获次数设置捕获函数,引入捕获参量q,在缺陷目标范
围内提取缺陷节点位置为:
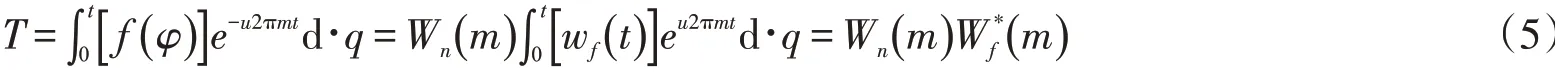
上述计算表达式中:T表示离散变换条件下,捕获函数的傅里叶计算节点位置[7];f(φ)表示捕获程度;φ表示捕获函数自变量;e表示指数函数;u表示捕捉频率;m表示共轭值;t表示目标范围空间;k表示d为求导符号;wf(t)表示实时缺陷信号;Wn(m)表示n次捕获下的系统捕获强度定值;Wf*(m)表示捕获强度为f时,对内存文件缺陷的捕获实际强度,*表示变换标志.参照图2中的坐标系,根据捕获函数,提取图1中的缺陷节点位置[8].
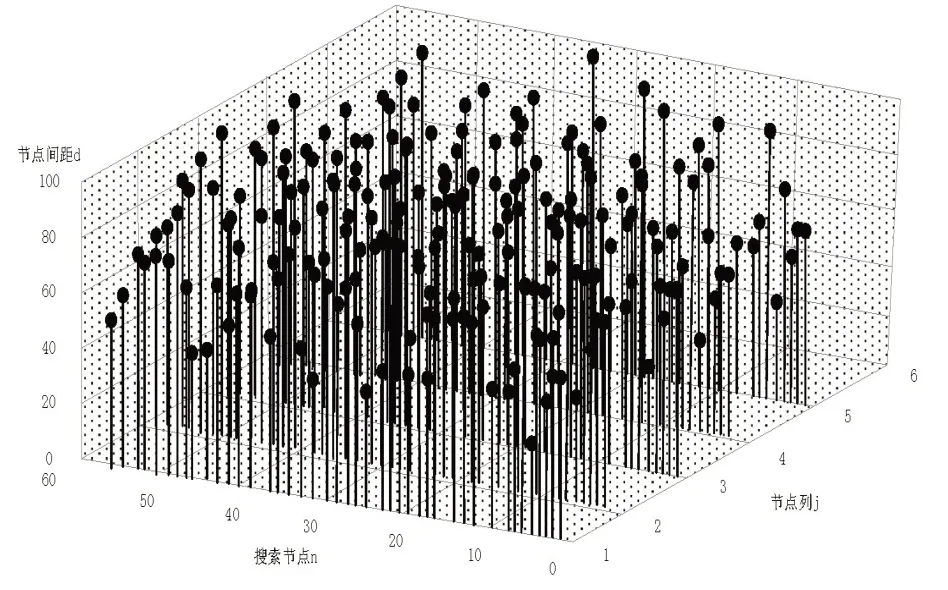
图1缺陷一次界定范围 Fig.1 Range of defects defined once
该坐标系将涵盖的正常节点数量,降到最小,利用公式(5)设置捕获指令,得出缺陷目标函数中的缺陷节点,为接下来的定位作铺垫.
1.3计算缺陷中心节点 在得到的缺陷节点中,随机选取两个相邻的缺陷节点作为样本,通过距离缩放法计算缺陷中心节点,选取的缺陷样本如图3所示.
选取的缺陷样本,需要满足两个峰值的基本要求.对文件系统中的缺陷数据进行“平坦”处理,假设“平坦区域”中,高峰值和次峰值的横坐标为a和b,计算区域中心位置s0和峰值宽度z,如下式所示:

公式(6)中:τ表示峰值数量,同时τ≥2;ε表示误差修正系数;μ表示宽度衡量参数.根据上述中的计算结果,确定缺陷节点与缺陷中心位置的距离,根据实时变化的缺陷强度指标,结合公式(6),计算随机动态变化参量k,公式为:

公式(7)中:δ表示缺陷峰值调节控制因子[9];d0表示对动态参量的调节因子;α表示缺陷在强度不同的峰值活动方向.引入激活函数的线性回归模型:

公式(8)中:n表示共享系统内存文件中的多峰值缺陷节点个数;y(t)表示期望输出值;qi(t)表示在系统i缺陷段的计算回归因子;pi表示缺陷节点之间的连接权重;ω(t)表示计算残差.根据该模型结合变化参量k,得出缺陷中心节点:

根据得出的中心坐标位置,确定该缺陷的边缘,得出缺陷位置的具体范围.
1.4获取边界坐标 利用最小二乘法获取缺陷中心节点以外的边界坐标,实现对系统缺陷的精准定位[10].根据上述计算得到缺陷中心c,假设距离该中心有n个锚节点,在确定的缺陷目标范围内,每一坐标可用a1,a2,…,an来表示,则对应每一锚节点,存在an={( x,y)|( x1,y1),( x2,y2),…,( xn,yn)},设置一个未知节点为ak,该节点坐标为( xk,yk),假设该节点是该缺陷的真实坐标,则未知节点与锚节点的关系为:

公式(10)中的d1,d2,…,dn,表示未知节点与锚节点之间的估计距离.通过该公式得到的坐标边界获取示意图如图4所示.
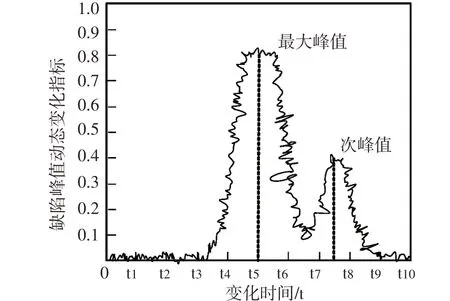
图3缺陷峰值示意图 Fig.3 Diagram of peak defects
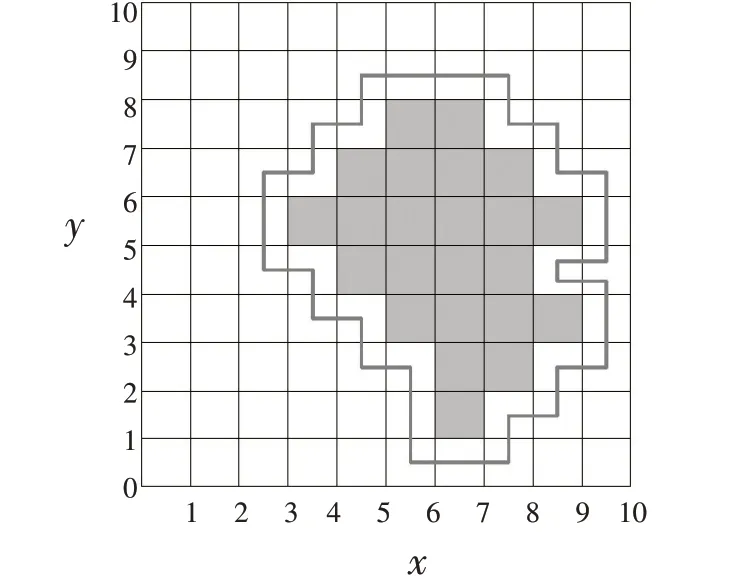
图4缺陷边界坐标获取示意图Fig.4 Diagram of defective boundary coordinate acquisition
根据图4可知,图中灰色区域代表缺陷真实范围,利用最小二乘法,得到边界坐标.将公式(10)改写成Ax=b的形式,并利用最小二乘法进行求解,得出目标函数Min‖ Ax-b‖2,求解得出:

公式(11)中:x′、y′表示缺陷边界的横坐标与纵坐标.通过该计算过程,得出图4中缺陷的具体边界坐标,确定该缺陷在文件系统中的覆盖范围,至此实现对高效共享系统内存文件缺陷位置的定位算法.
2 仿真实验
为证明所提出算法的实用性和严谨性,针对此次研究提出仿真对比实验,通过该实验检测数据,增强对此项定位算法功能特性的说明,同时引入传统缺陷定位算法,对比两种算法在缺陷定位上的差异.
2.1实验准备 选用的计算机装有3.60 MHz双核处理器,该计算机型号为ADMR52600X,显存容量为4 GB,内存容量为8 GB,主板芯片类型为AMDA320;载入Windows 2019a操作系统,设置3级缓存程序,每一级的基本配置为96 KB、298 0 KB以及30 MB.本次实验的测试工具为FlexibleI/O和Filebench,利用该工具测试算法的定位性能.设置该实验测试系统带宽,如表1所示,通过不同带宽条件,进行多次仿真实验测试,确保测试结果的真实性和一致性.
随机挑选一组共享系统内存文件作为实验对象,将其载入到内存文件中,设置多个访问客户端对该系统执行访问操作.同时模拟多个强度不一、位置不均、缺陷范围不同的系统缺陷,其中的部分缺陷模拟内容如图5所示.
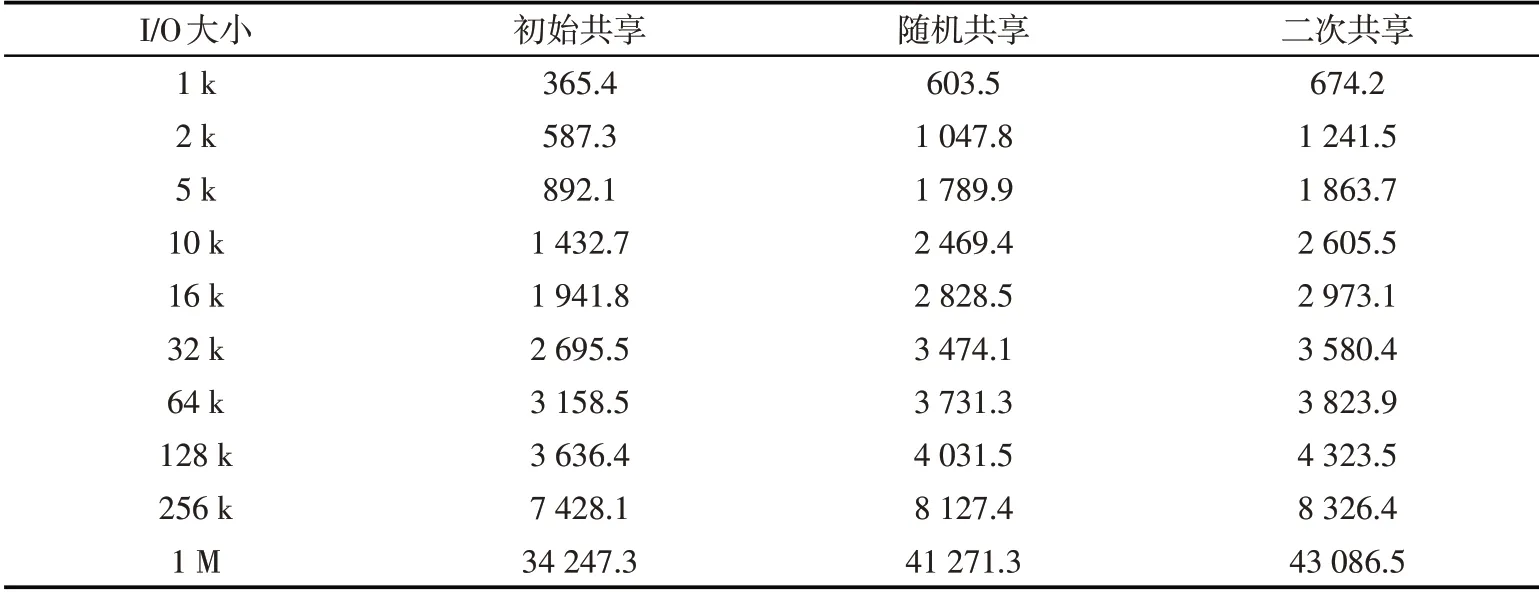
表1实验测试带宽参数Tab.1 Experimental test bandwidth parameters
图5是模拟的4种类型不同的缺陷情况,其中,类型A为集中型缺陷;类型B为混合型的交叉缺陷;类型C为分散型缺陷;类型D为影响范围较大的缺陷.实验准备阶段设立完毕后,载入测试系统并运行,当系统运行正常可以开始实验.
2.2结果分析 分别利用两种算法对系统中的缺陷进行定位,分析两种算法对缺陷位置的定位效果.其中,实验组为所提出算法的测试结果;对照组为传统方法的测试结果.引入C类型的缺陷,定位对比测试结果如图6所示.
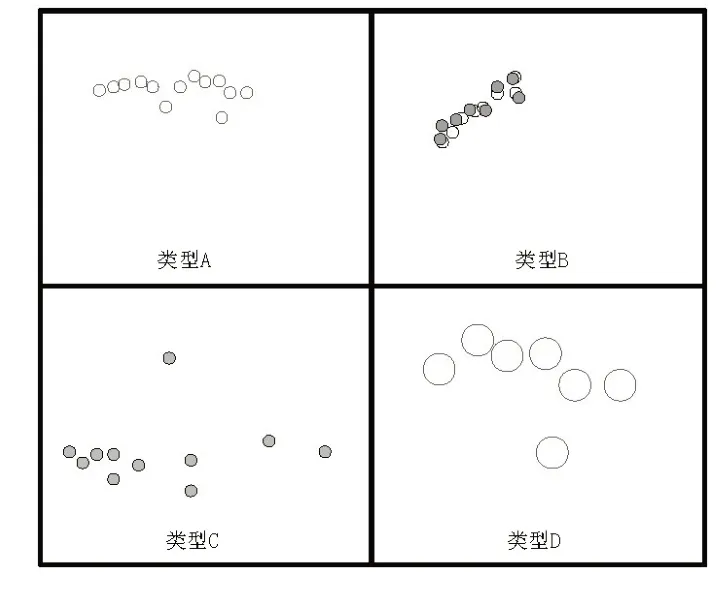
图5模拟实验条件 Fig.5 Simulated experimental conditions

图6分散性陷定位的算法对比结果Fig.6 Comparison of the algorithm for locating discrete traps
分析图6可知,所提出算法准确找到模拟缺陷的中心位置,并正确计算出缺陷边界坐标,使得定位算法准确捕获到系统中的缺陷位置;而传统的定位算法,由于得到的中心点位置不精准,对缺陷边界坐标的计算存在较大误差,导致定位的缺陷范围与缺陷实际不相符.为确保实验结果可靠,再对系统中的B类型缺陷进行定位,得出图7所示的测试结果.
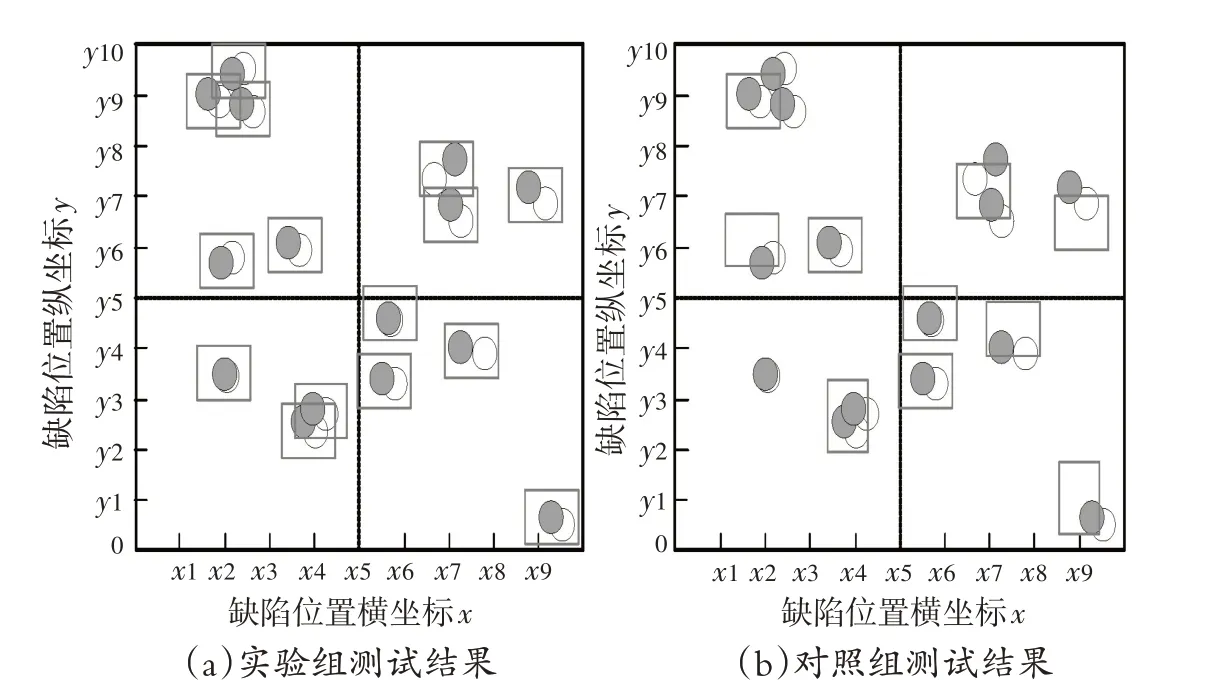
图7混合型缺陷定位的算法对比结果Fig.7 Comparison of algorithms for hybrid defect location
根据图7可知,面对混合型的系统缺陷,所提出算法同样精准定位缺陷中心位置,以此作为计算原点,得到准确的边界坐标,实现全方位缺陷定位;而传统的定位算
法,面对复杂定位,计算的缺陷中心受缺陷类型影响,得出的位置节点严重偏离实际,无法得到准确的缺陷位置.综合上述测试结果可知,本文所提出算法在第一步即实现了严谨性、精准性这一研究要求,因此得到更加精准的定位结果.
3 结束语
本文提出的系统缺陷定位算法,融合了数学原理,增强定位算法的计算能力,使得到的定位结果真实可信,解决了传统算法存在的偏差问题,为今后的共享系统文件缺陷定位提供技术保障,也为其他系统的缺陷检测提供算法的优化思路.但此次研究仍存在计算量较大的局限,需要进行更深入的研究,进而提高算法在实际使用中的性能.

