离散大系统的部分联结不稳定性的判定
孙水玲
(广州工商学院,广东 广州510850)
许多实际问题建立的系统(如工业系统、城市交通网系统、环境系统、经济系统、社会系统等)往往变量很多,造成系统的维数很高,给系统稳定性的研究带来很大的困难.为了解决这些问题,文献[1]给出大系统的方法,即把复杂系统视为若干相互联结的低阶子系统相互作用的动态大系统,然后通过子系统及其关联性质,给出大系统的稳定性的研究.关于这方面的研究结果已有很多.但对于一个已经建立了数学模型的大型动力系统,虽然考虑了各子系统间的关联,然而它们关联的强度可能会有很大的不同,而且一组子系统可能暂时与其他子系统分离也会导致大系统结构上的变化,为此文献[1]提出了一套关联稳定性理论.由于有些大系统中部分关联固定,而只有部分关联可以变化,因此文献[2]给出部分关联稳定性概念,文献[3-7]给出了离散大系统的部分关联稳定性的一些研究结果.本文主要利用向量李雅普诺夫函数法及比较原理,讨论非线性离散大系统和常系数线性离散大系统的部分联结不稳定性,给出了部分关联不稳定性的充分条件.
1 主要结果
首先考虑具有r个子系统的n阶非线性离散大系统:

其中:

证明 取大系统(1)的向量李雅普诺夫函数:

得到:
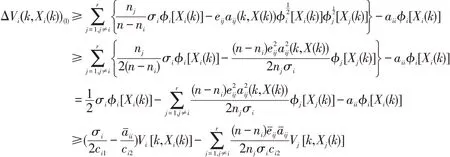
即有:
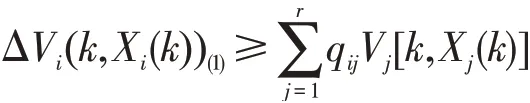
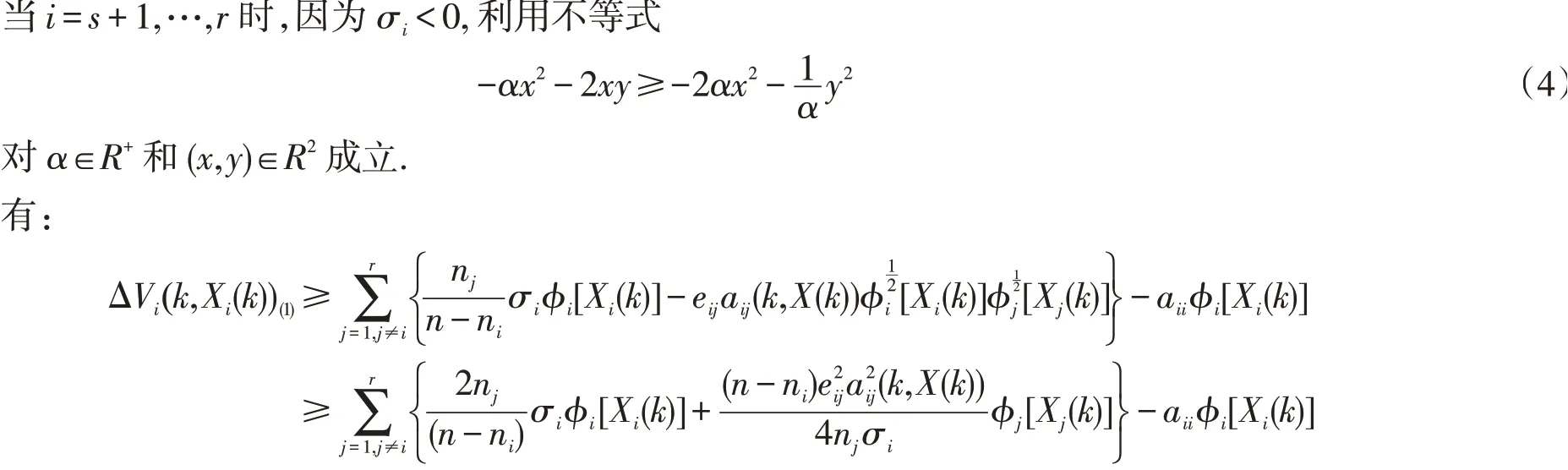
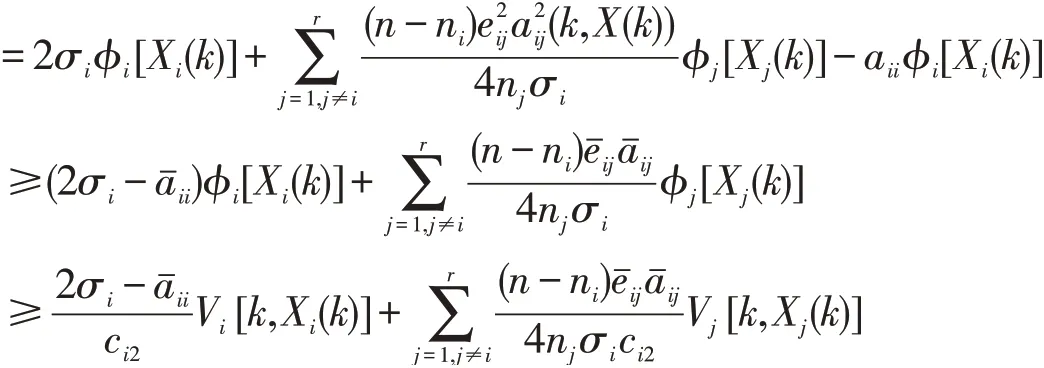
同样有:

考虑具有r个子系统的n阶线性定常离散大系统.
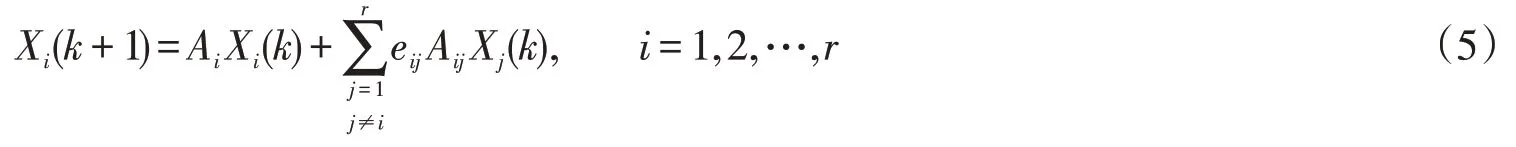
其中,Ai为ni×ni阶常数矩阵,Aij为ni×nj阶常数矩阵,它表示系统j对系统i的作用(i,j=1,2,…,r,j≠i).Xi=(x1(i),x(
2i),…,xn(ii))T为ni维状态分量,而且n1+n2+…+nr=n.X=(X1,X2,…,Xr)T为n维状态向量.
系统(5)的孤立子系统为:

以下假设离散大系统(6)的每个子系统,都存在ni×ni阶负定对称矩阵Bi和常数μi使负定函数

满足:



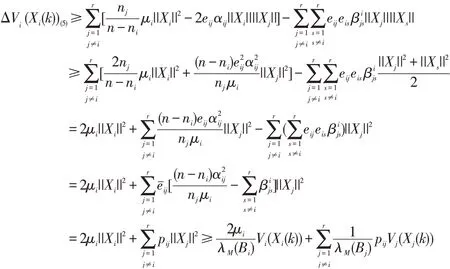
所以,
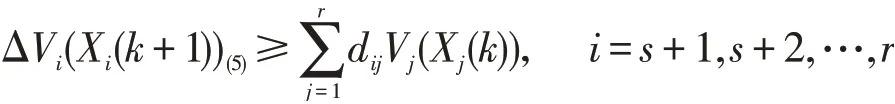

2 结论
本文中的关联矩阵E随着时间k变化时,定理仍然成立,而且关联因子eij可以取[0,1]上的任何数值,即定理适用于关联因子随时间是变化的情况.

