脉动流条件下棒束通道阻力特性研究

祁沛垚，李 兴，邓 坚，于晓勇，谭思超,*

(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001;2.武汉第二船舶设计研究所，湖北 武汉 430205；3.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

在核反应堆的设计运行中，堆芯流动阻力影响回路的流量分配、系统不稳定性的确定以及自然循环水平，因此燃料组件内阻力的计算与反应堆的安全与运行密不可分。近年来，核电系统中的脉动流问题逐渐引起人们的广泛关注。反应堆受事故工况或海洋环境影响时，堆芯冷却剂流量瞬态波动状态改变了系统的阻力特性，直接对反应堆的安全运行产生影响，因此，有必要对燃料棒束在流量波动条件下的阻力特性进行研究。

国内外学者针对稳态流动下燃料组件的单相阻力特性开展了大量研究[1-3]。由于棒束通道几何结构的复杂性，大部分研究结果都是基于试验方法得出的摩擦阻力系数经验关系式。Rehme[1]通过试验和理论结合的方法，导出了计算燃料棒束通道中层流和湍流的摩擦阻力系数计算公式。Su等[4]、Bae等[5]通过积分流动区域的速度分布，得到了燃料棒束通道中的湍流摩擦阻力系数。然而，它们的计算过程非常复杂，所以没有得到广泛应用。Cheng等[6]提出棒束通道的阻力主要取决于结构和通道类型，他们将燃料棒束中的流动划分为不同的流动区域，并分别计算了摩擦阻力系数。所得公式已广泛应用于燃料棒束阻力的预测。另外，定位格架的阻力特性也是研究者关注的焦点。但由于定位格架结构的多样性，且定位格架下游流动复杂[7-8]，很难提出一个通用的计算定位格架流动阻力的公式。Rehme[9]基于定位格架占据流道面积与流量面积的比值提出了定位格架局部阻力特性预测公式，但其并不能很好地预测试验结果。Chun等[10]在Kim等[11]模型的基础上进行修正，基于定位格架区域流体的受力平衡，建立了新的计算关系式，认为定位格架的总阻力包含定位格架和交混叶片的局部阻力、棒束的摩擦阻力等。

针对流量波动因素对阻力特性的影响，国内外学者也开展了一系列研究。Hershey等[12]研究了圆管内脉动流的流动阻力。结果表明，当脉动流频率高于某一特定值时，脉动流的摩擦系数和能量损失明显大于稳态流。Ohmi等[13]通过大量试验将脉动流分为准稳态流子区(ω′1/2<1.32)、中间流子区(1.32<ω′1/2<28)和惯性子区(28<ω′1/2)。当流体处于准稳态时，脉动流的特性与稳态流摩擦系数相似。当流体处于中间流子区和惯性子区时，周期平均摩擦阻力系数大于相同周期平均雷诺数时的稳态流动。刘宇生等[14]、张川等[15]分析了脉动振幅和周期平均雷诺数对矩形通道内阻力特性的影响和作用机制。Zhuang等[16]通过理论分析和试验研究了不同脉动参数下窄通道中层流和湍流的阻力特性，并得出不同的通道形状对脉动流阻力特性有很大的影响。

综上所述，针对脉动流下常规通道不同流态的阻力特性研究较多，而对于复杂通道棒束通道的流量波动下阻力特性研究较少。因此，本文以此为背景对复杂棒束通道的摩擦阻力及定位格架局部阻力特性进行研究。

1 试验装置与方法

1.1 脉动流试验平台

棒束通道压降测量在哈尔滨工程大学激光诊断试验平台上进行[17]，系统回路如图1所示。试验过程中数据采集系统的总采样率为25次/s，足以跟踪低频脉动流特性。为抑制离心泵产生的旋涡结构，在管束通道下腔安装了蜂窝结构的均流板用以消除棒束通道入口效应的影响。

图1 试验回路

图2a为试验所用典型5×5布置的棒束通道，通道内包含25根直径9.5 mm的棒，棒间距12.6 mm，边缘棒束距通道壁面2.55 mm。棒束流道为65 mm×65 mm的正方形通道，试验段全长1 100 mm(图2b)。棒束通道内装有带交混叶片的定位格架，定位格架示意图如图2c所示，其由条带、弹簧、钢凸以及交混叶片组成。试验中通过正方形通道中心的引压孔连接导压管与两个压差传感器，分别用来测量沿程摩擦阻力和局部阻力。两压力传感器高、低压端距离分别为L1=300 mm、L2=240 mm。脉动流的控制方式详见文献[18]。脉动流精度验证示于图3，可看出，预测值与测量值一致，且周期平均雷诺数、周期和振幅的最大相对偏差分别不超过0.075%、0.03%和0.13%。

1.2 数据处理与不确定度分析

在稳态流动条件下，由压差传感器测量的压降Δp包括3个部分，即摩擦压降Δpf、重力压降Δpg和定位格架局部压降Δpsg。

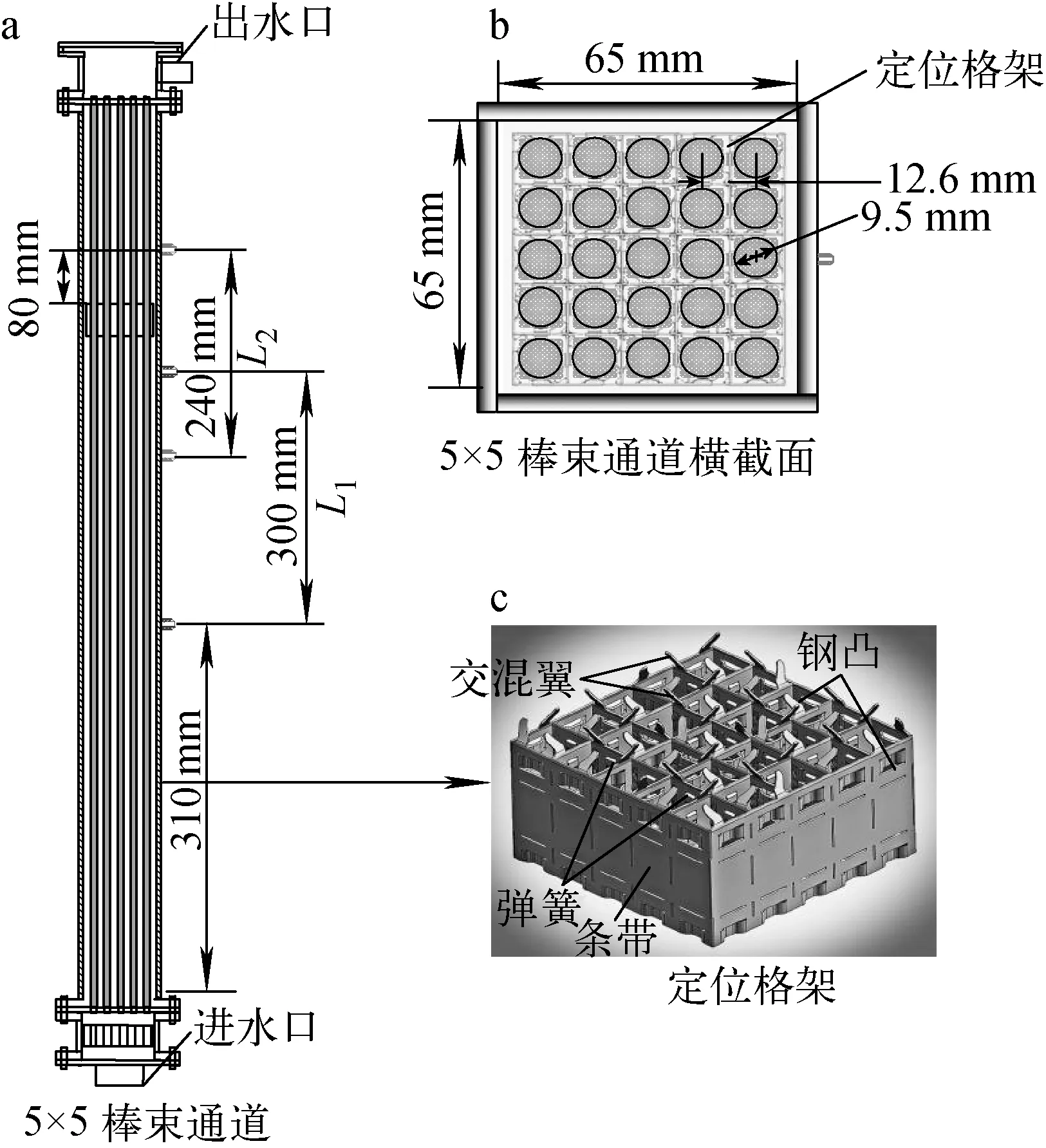
图2 棒束通道尺寸与定位格架结构

图3 脉动流精度验证

(1)

因此，棒束的摩擦阻力系数λ和定位格架的局部阻力系数ksg计算如下：

(2)

(3)

式中：Um为瞬时横截面平均速度；ρ为流体密度；Dh为棒束通道的水力直径。

对于时间和空间上充分发展的脉动流，其瞬时截面平均速度可用式(4)表示。

Um=Um,ta+ΔUmsin(ωt+∠φ1)

(4)

式中：Um,ta为脉动流棒束通道内周期平均流速；ΔUm为脉动流最大波动幅度；ω为角速度；t为时间；∠φ1为脉动流相位角。脉动振幅定义为Au=ΔUm/Um,ta。

脉动湍流的动量积分方程可写成：

(5)

其中，τw为壁面剪应力。瞬时摩擦阻力系数λf可由式(6)计算：

(6)

结合式(5)、(6)，脉动流的瞬时摩擦阻力系数可写成式(7)形式：

λf(t)=

(7)

在测量过程中压差传感器的响应时间约为100 ms，流量计的响应时间约为50 ms，在对瞬态摩擦阻力系数λf(t)的计算过程中采用阶跃试验去除二者间的相位差使得流速与压降一一对应。对式(7)在1个周期内进行积分，得到周期平均摩擦阻力系数：

(8)

此外，本文还讨论了脉动流分析中常用的一些无量纲参数：Womersley数，也称无量纲频率，ω′1/2=(Dh/2)(ω/ν)1/2；周期平均雷诺数，Reta=Um,taDh/ν。

试验结果的不确定度取决于测量过程中测量仪器和测试部分的精度，表1列出了相应仪器的测量范围和误差。根据Moffat[19]方法的误差传递公式(式(9))，计算得到雷诺数的相对误差为1.53%，摩擦阻力系数和局部阻力系数的相对误差分别为1.87%和1.23%。本文试验在室温(25 ℃)和常压(0.1 MPa)下进行。

(9)

式中：σF为计算结果的误差；F为变量pi的函数；σi为变量pi的误差。

表1 测量参数和仪器误差

2 结果与讨论

2.1 稳态条件下阻力特性分析

为保证结果的可靠性，需对试验装置进行验证。验证方法是将稳态条件下的摩擦阻力系数与经验公式进行比较。

图4a为试验测量得到的摩擦阻力系数与Cheng公式和Blasius公式预测的摩擦阻力系数之间的对比。结果表明，棒束通道内层流与湍流之间没有明显的过渡点，但存在较大的过渡区。这可认为是由棒束的复杂结构引起的，当棒束通道子通道中心区域达到湍流状态时，由于黏性力的影响，棒壁附近仍可能处于层流状态，因此棒束通道并没有明显的转捩点。从图4a可看出，层流试验结果与Cheng公式预测值吻合较好，相对误差小于3%。然而，随着雷诺数的增加，试验结果逐渐低于Cheng和Blasius公式的预测。本试验中层流与湍流的转捩雷诺数约为900，略小于Cheng等公式计算的预测值1 076。

图4b为试验测量得到定位格架局部阻力系数与Chun、Zhu等公式的对比。结果表明，他们的经验公式能合理地预测局部阻力系数随雷诺数的变化趋势，但并不能精确地预测试验值。这可能是由于定位格架结构形式多样所造成的，本文所研究的定位格架包含了弹簧、钢凸以及交混叶片，与其他学者所使用的定位格架有一定的区别。为预测试验的局部阻力系数，通过将试验数据与不同流型下的雷诺数拟合，建立了局部阻力系数的关联式：

ksg=aReb

(10)

其中：Re<1 845时，a=613，b=-0.72；Re<5 925时，a=1 845，b=-0.487 9；Re>5 925时，a=23，b=-0.32。经过对比，定位格架稳态条件局部阻力系数预测值与试验值的相对误差在6%以内。

2.2 流量脉动参数对瞬态阻力特性的影响

图5为Reta=6 165时周期和振幅对瞬时摩擦阻力系数的影响。从图5a可看出，棒束通道内摩擦阻力系数沿环形曲线顺时针方向变化。相同雷诺数下，加速条件下棒束通道内摩擦阻力系数大于稳态流动下对应雷诺数下的摩擦阻力系数，减速条件下棒束通道内摩擦阻力系数小于稳态流动下对应雷诺数下的摩擦阻力系数。Qi等[7]使用粒子图像测速(PIV)对棒束通道内脉动流速度场进行了研究，结果表明，当通道内流体处于加速周期时，壁面附近流速大于稳态值，这使得壁面附近速度梯度增大，从而导致摩擦阻力系数大于稳态值，减速周期则正好相反。

对比图5a不同脉动周期的雷诺数-摩擦阻力系数曲线可看出，随着脉动频率的减小，环形曲线的宽度逐渐缩小，脉动流与稳态流动下棒束通道内摩擦阻力系数的差异逐渐减小，且减速和加速条件下的摩擦阻力系数与稳态值近似对称。图5b为相同脉动频率、不同脉动振幅下得到的雷诺数和摩擦阻力系数环形曲线。从图5b可看出，流量脉动振幅越大，摩擦阻力系数在层流区跨度就越大，且在雷诺数较小时展现出的摩擦阻力系数偏移越明显，这说明非稳态流动对低流量的影响更明显。造成这一现象的原因可能是当脉动流处于流速较小的层流区时，流体主要靠分子相互作用传递动量，而湍流条件下动量传递速率远大于层流。因此，对于由压力驱动的脉动流，当脉动流量波动到流速较小的层流区时，棒束通道内流场对压力的响应能力将会下降，故导致棒束通道内摩擦阻力系数变化滞后于流场变化，进而造成流速较小时棒束通道内摩擦阻力系数偏离稳态值。

图4 稳态条件下阻力系数

图5 脉动周期和振幅对棒束通道阻力特性的影响

2.3 脉动流下周期平均阻力特性分析

周期平均摩擦阻力系数的研究对脉动流条件下系统能量损失具有重要意义。图6a为不同平均雷诺数、脉动频率和振幅下棒束通道内周期平均摩擦阻力系数的变化曲线。可看出，脉动条件下的周期平均摩擦阻力系数明显大于稳态条件下的摩擦阻力系数。这可能是因为加减速流动增加了流体能量的耗散，表现为脉动流周期平均摩擦阻力系数的增加。此外，还发现周期平均摩擦阻力系数受脉动幅值和无量纲频率的影响。它随着振幅Au和无量纲频率ω′1/2的增加而增加。结合图5可知，随着脉动幅值和无量纲频率的增大，λf-Re曲线倾角呈向上的环形曲线，这导致瞬时摩擦阻力系数高于稳态值的比例增大，从而使得周期平均摩擦阻力系数大于对应雷诺数下的稳态值。图6b为周期平均局部阻力系数随不同脉动流参数的变化曲线，可看出，脉动流下平均局部阻力系数同样大于稳态值，且变化趋势与摩擦阻力系数类似。

为研究脉动流对棒束通道内摩擦阻力和定位格架局部阻力贡献特点，将脉动周期平均值和对应雷诺数下稳态流动阻力系数相除，定义如下无量纲参数：

Cf=λta/λst

(11)

Csg=kta/kst

(12)

式中：λst和kst为稳态流动下棒束通道内摩擦阻力系数和定位格架局部阻力系数；λta和kta为1个脉动周期的平均摩擦阻力系数和定位格架局部阻力系数。

通过改变ω′1/2、Au和Reta研究不同脉动参数对Cf、Csg的影响，结果示于图7。从图7a可看出，当脉动频率恒定时，脉动振幅增加，Cf和Csg呈现指数变化的趋势。此外，对比Cf和Csg可发现，定位格架的局部阻力系数受幅值变化的影响较小，这可能是由于定位格架内的阻力主要来自于钢凸、弹簧、条带和交混叶片的局部阻力，脉动流对定位格架流体速度分布变化所引起的阻力特性的影响是有限的，这说明定位格架的复杂结构可有效抑制脉动流影响。从图7b可看出，当脉动振幅恒定时，脉动频率增加，Cf和Csg单调增加，且图7中Cf和Csg皆随Reta的增加而减小。上述结果说明，脉动流的影响随ω′1/2和Au的增加而增加，随Reta的增加而减少。

图6 不同脉动形式下棒束通道内周期平均阻力系数

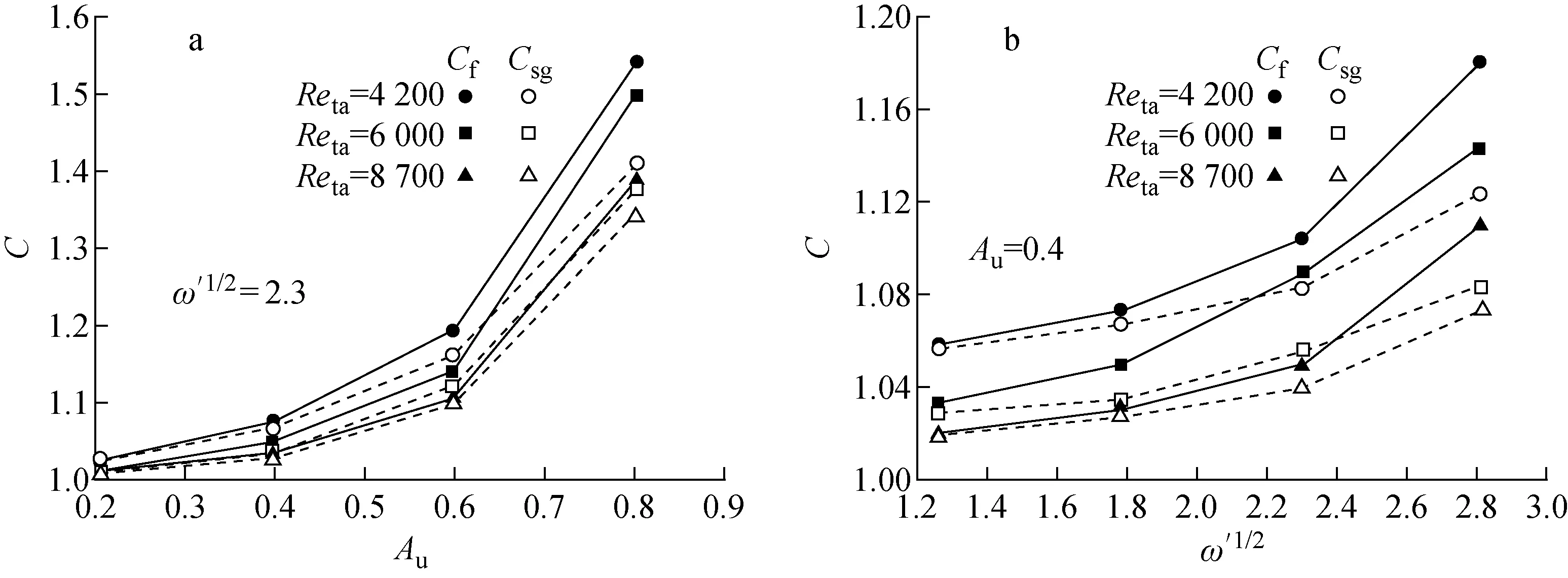
图7 脉动参数对棒束通道阻力系数的影响

脉动流摩擦阻力改变是由于加速度使湍流区的流动行为产生较大变化，根据α=dU/dt，得最大加速度αmax=2πΔU/t0。为研究加速度对脉动流的影响，引入无量纲加速度α*。

(13)

从式(13)可看出，无量纲加速度由脉动振幅、无量纲频率以及周期平均雷诺数3个脉动流参数组成，因此通过分析α*即可分析各种脉动参数耦合作用对棒束通道阻力特性的影响。图8为无量纲加速度对流动阻力特性的影响。从图8可见，随α*的增加，C增加，伴随着脉动流动的阻力贡献增加，说明脉动频率、脉动振幅、平均雷诺数三者之间相互作用，无量纲加速度增加时，脉动流的阻力随之增加。

图8 无量纲加速度对流动阻力特性的影响

基于上述研究，发现脉动流下棒束通道摩擦阻力系数和定位格架局部阻力系数受到Au、ω′1/2和Reta的共同作用。为能预测脉动流下棒束通道内平均摩擦阻力特性和局部阻力特性，根据π定理，脉动流压降模型建立如下：

π=f(π1,π2,π3,…,πn)

(14)

F(Δp,ρ,u,l,μ,αmax)=0

(15)

π1=Δp/ρu2，π2=l/d,

π3=αmaxd/u2,π4=μ/ρud

(16)

用基本量纲表示各物理量，根据方程一致性原则，可得脉动流压降计算公式：

(17)

基于试验数据，得到脉动流周期平均摩擦阻力系数的拟合关系式：

(18)

使用同样方法，得到周期局部阻力系数拟合公式：

(19)

(20)

为评估拟合关系式的预测结果，将预测的周期平均阻力系数与试验数据进行对比，如图9所示。结果表明，与试验数据相比，预测的周期平均摩擦阻力系数和局部阻力系数的相对误差分别在15%和10%以内。

3 结论

本文通过试验系统研究了脉动流条件下周期平均雷诺数Reta、脉动振幅Au、无量纲频率ω′1/2对棒束通道压降的影响，并通过量纲分析，建立了脉动流下棒束周期平均摩擦阻力系数和定位格架周期平均局部阻力的预测关系式，得到如下典型结论。

图9 棒束通道平均压降试验值与理论值对比

1) 脉动条件下，定位格架的周期平均局部阻力系数和棒束通道的周期平均摩擦阻力系数相比于对应雷诺数下的稳态值明显增大，且增大的比例随脉动振幅和频率的增大而增大，随时均雷诺数的增大而减小。脉动加速度是影响周期平均摩擦阻力系数的主要因素。

2) 流体加速会导致瞬时摩擦阻力系数大于对应雷诺数下的稳态值，减速会使瞬时摩擦阻力系数小于对应雷诺数下的稳态值，且这一偏离值随流体雷诺数的减小而增大。

3) 在相同脉动流参数下，定位格架阻力系数比值Csg大于沿程摩擦阻力系数比值Cf，说明定位格架的复杂结构具有一定抑制脉动流的效果。

4) 根据试验结果，拟合了棒束通道周期平均摩擦阻力系数和定位格架局部阻力系数的预测关系式，二者预测值和试验结果误差分别在15%和10%以内。