Solving flexible job shop scheduling problem by a multi-swarm collaborative genetic algorithm

WANG Cuiyu,LI Yang,and LI Xinyu

School of Mechanical Science and Engineering,Huazhong University of Science and Technology,Wuhan 430074,China

Abstract:The flexible job shop scheduling problem (FJSP),which is NP-hard,widely exists in many manufacturing industries.It is very hard to be solved.A multi-swarm collaborative genetic algorithm (MSCGA) based on the collaborative optimization algorithm is proposed for the FJSP.Multi-population structure is used to independently evolve two sub-problems of the FJSP in the MSCGA.Good operators are adopted and designed to ensure this algorithm to achieve a good performance.Some famous FJSP benchmarks are chosen to evaluate the effectiveness of the MSCGA.The adaptability and superiority of the proposed method are demonstrated by comparing with other reported algorithms.

Keywords:flexible job shop scheduling problem (FJSP),collaborative genetic algorithm,co-evolutionary algorithm.

1.Introduction

Scheduling is an important aspect of planning in current manufacturing systems;production scheduling allocates relative production resources to tasks and order to meet all constraints and optimization goals [1−3].Therefore,the scheduling technology can improve manufacturing efficiency by reducing scheduling conflicts,and reducing process time [4].In modern manufacturing system,intelligent systems and machines are used to improve production efficiency [5].The intelligent systems and machines are widely used in modern manufacturing systems so that the same machine can perform multiple operations.[6].In this case,the flexible job shop scheduling problem(FJSP) has attracted increasing attention because it considers machine flexibility [7].

The FJSP is a typical scheduling problem in modern manufacturing systems [8,9].It is also an NP-hard problem [10].In 1990,Brucker &Schile [11]first presented this problem and some methods to solve it.The methods to solve the FJSP primarily include the genetic algorithm(GA) [12,13],the iterated greedy algorithm [14],the tabu search (TS) [15],the variable neighbourhood search algorithm (VNS) [16],the particle swarm optimization(PSO) algorithm [17]and some hybrid algorithms[18,19].The results of research on the FJSP are also applied to several practical cases [20−22].

The FJSP can be decomposed into two different subproblems:machine selection (MS) problem and operation sorting (OS) problem.At present,unified coding is usually used to solve the problem.However,due to the different characteristics of these two sub-problems,unified coding will make the solution space more complex,which is not conducive to the solution of the algorithm.Therefore,to solve the FJSP,a multi-swarm collaborative genetic algorithm (MSCGA) based on the collaborative optimization algorithm is proposed [23−25].The collaborative evolutionary algorithm simulates the evolutionary process of interaction between two species in nature.[26].While a species is evolving,it interacts with and adapts to other species.This situation is similar to that of the two sub-problems in the FJSP.In this algorithm,the coevolution of different populations is used to solve two sub-problems.The experimental results demonstrate that the proposed MSCGA algorithm has obvious advantages.

The main innovation of this paper is to combine the characteristics of the FJSP,combining the advantages of the evolutionary algorithm and collaborative optimization to improve the GA.This outcome indicates that the proposed approach is an effective method to use in FJSP research.

The remainder of this paper is organized as follows.Section 2 provides details on the literature review.Section 3 describes the problem formulation.Section 4 pre-sents the MSCGA-based approach for solving the FJSP.Section 5 reports the experimental results.Section 6 discusses the conclusions and future studies.

2.Literature review

After the FJSP was first presented in 1990,many solving methods have been published.At present,there are two categories to solve permutation flow shop scheduling problem (PFSP):the exact method and the approximation method.

Brucker &Schile [11]presented this problem firstly and proposed a polynomial graphical algorithm.Gomes et al.[27]presented a new integer linear programming model and used commercial software to solve it.However,it is difficult to obtain a satisfactory solution in a short time when an accurate algorithm is used to solve largescale problems [12].Therefore,approaches used for solving the FJSP focus on approximation methods [7,10].

Kacem et al.[28]used a localization approach to address the MS sub-problem and applied a GA to solve the OS sub-problem.Ho et al.[29]proposed a learnable genetic architecture (LEGA).Yin et al.[30]proposed a multi-objective genetic algorithm to solve the FJSP.Homayouni et al.[13]proposed an operation-based multistart biased random key genetic algorithm (BRKGA)coupled with greedy heuristics for the FJSP with transportation.Shi et al.[31]proposed a multi-population genetic algorithm (GA) with an Erdos &Renyi (ER) network for solving the FJSP.Chen et al.[32]presented a self-learning genetic algorithm for FJSP.Ding et al.[17]proposed an improved PSO algorithm.By improving the encoding/decoding scheme,a good solution was obtained.Ricardo and Arturo [19]proposed a Pareto approach for the FJSP with process plan flexibility.Lu et al.[33]presented a new multi-objective discrete virus optimization algorithm.Li et al.[12]improved the Jaya algorithm to solve the FJSP with transportation and setup times.Alejandro et al.[34]showed a biomimicry hybrid bacterial foraging optimization algorithm for the FJSP.Ding and Gu [17]improved the PSO algorithm for the FJSP by considering a new encoding and decoding method.

There are also several hybrid algorithms for the FJSP.Zribi et al.[35]proposed a hierarchical method for the FJSP.Gao et al.[36]proposed a hybrid genetic for solving the FJSP.The variable neighborhood descent algorithm is also used to speed up the search process of the GA algorithm.Li et al.[18]proposed a hybrid GA and TS algorithm for the FJSP and achieved good results.Wu et al.[37]presented a hybrid pigeon-inspired optimization and simulated annealing algorithm for the FJSP.

In this paper,the MSCGA is developed for the FJSP.Few papers have used the co-evolutionary algorithm to solve this problem [38].Only Rou et al.[39],Xing et al.[40]and Shi et al.[31]have designed three co-evolutionary algorithms for solving the FJSP.Therefore,it is compared to these three algorithms.The proposed method obtains better results than these algorithms.

3.Problem model

There exists a set of n jobs J={J1,J2,J3,···,Jn} and a set of m machines M={M1,M2,M3,···,Mm}.Each job Jiconsists of a sequence of operations {Oi1,Oi2,Oi3,···,Oini}where niis the number of operations in Ji.Each operation Oij(i=1,2,···,n;j=1,2,···,ni)must be processed by one machine in a set of given machines Mij⊆M [18].

The scheduling goal of this paper is to minimize the maximal completion time,also known as the makespan.It contains two sub-problems,making the FJSP become more complex and challenging [29].

The hypotheses considered in this paper are summarized as follows [7]:

(i) All machines and jobs are available at time zero.

(ii) No precedence constraints among operations of different jobs.

(iii) Each job cannot be processed by two machines at the same time and each machine can only perform one operation at the same time.

(iv) The transfer time between machines is assumed to be negligible.

4.The proposed MSCGA for solving FJSP

4.1 Optimization strategy of MSCGA

Because of the collaborative optimization strategy,the proposed MSCGA explores the solution space of the MS and OS separately and collaboratively.This optimization process is performed until the termination criterion is obtained.In this method,each job contains one MS swarm to determine the selected machines for each operation.There is one OS swarm to optimize the scheduling of all jobs.Under this optimization strategy,each swarm can choose its own algorithms.This helps ensure the most suitable algorithm for each swarm on the basis of its own features.In this study,the GA is used for each MS and OS swarm.Therefore,the overall process of the MSCGA proposed in this paper is as follows [26]:

Step 1Parameters setup.

Step 2Initialization.Generate N+1 swarms,where there are N MS swarms and one OS swarm,and select one individual from every N+1 swarm to form one FJSP solution.

Step 3Evaluation.Calculate the fitness value of each individual in the swarm and combine it with selected individuals from other swarms.

Step 4Terminate criteria satisfied? If yes,stop and output the results,otherwise go to Step 5.

Step 5Collaborative evolution.Generate new individuals for each swarm according to the genetic operators.Go back to Step 3.

4.2 Encoding and decoding

The encoding method in [18]is adopted in this paper.Because there are two types of swarms in this method,the two sub-problems require different encoding methods.

The encoding method of an operating system cluster is composed of job numbers.Assuming there are n jobs,the length of the OS string is equal toThe initial OS population is generated according to the encoding principle.

At length, one evening, the little hare, looking round for something to amuse him, noticed a great pot full of boiling water, so he strolled up to one of the hyaenas and said, Go and get in

Each MS swarm represents the MS of the corresponding job.The chromosome length is equal to the number of operations in the relative job.

An FJSP solution is made up by one OS individual and N MS individuals selected from the MS swarms one by one.[18].The procedure of decoding is as follows:

Step 1Generate the machine of each operation based on the MS string.

Step 2Determine the set of operations for every machine.

Step 3Determine the set of machines for every job.

Step 4Calculate the allowable starting time for every operation.

Step 5Check the idle time of the machine,and obtain the idle areas.Then,check these areas in turn.

Step 6Calculate the completion time of every operation.

4.3 Initial population and fitness evaluation

The operation-based encoding method is employed in this paper.Therefore,any chromosome can be decoded into a feasible solution.The optimization goal of this paper is to minimize the maximum completion time.

4.4 Genetic operators

Good and effective genetic operators are important for the proposed algorithm,as they can effectively handle the problem.There are three genetic operators in a GA:selection,crossover and mutation.This paper uses two different coding methods:OS swarms and MS swarms.In addition,these swarms have their own genetic operators.This operation is described in the following sub-sections.

4.4.1 Selection

In this paper,the OS swarms and MS swarms have the same selection operator.In addition,this paper uses two selection operators.The first one is the elitist selection scheme where the good fitness in parents is transferred to offspring.The other selection operator is the random selection operator.In this case,the algorithm will randomly select individuals for crossover and mutation operations.

4.4.2 Crossover

The OS swarm adopts precedence operation crossover(POX).With POX,the offspring effectively inherits good characteristics from the parents.The process for POX is shown as follows (P stands for the parent and O for the offspring):

Step 1Job set J={J1,J2,J3,···,Jn} is randomly divided into two groups Jobset1 and Jobset2.

Step 2Move the job in P1 that belongs to Jobset1 to the position O1;move the job belonging to Jobset2 in P2 to the position O2.

Step 3Put the remaining jobs in P2 into O1,and the remaining jobs in P1 into O2.

An example is shown in Fig.1.This example represents four jobs,and Jobset1={1,4}.

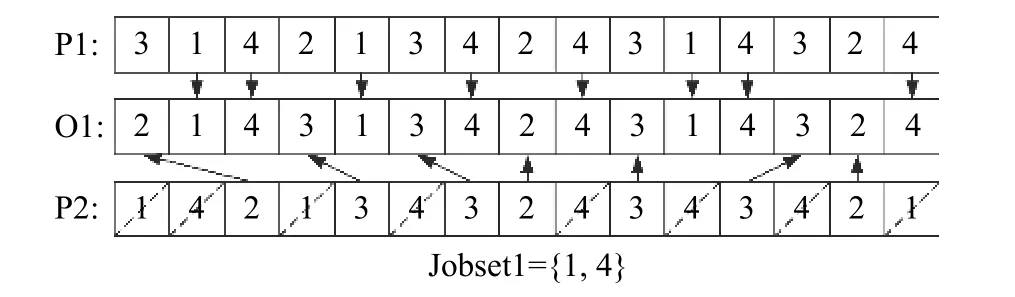
Fig.1 An example of POX for the OS swarm

In this paper,two-point crossover is used for MS swarm crossover operation.This crossover operation randomly chooses two positions at first.Then,this algorithm generates two child strings by swapping all elements between the positions of the two parent strings.This crossover ensures the generation of the feasible offspring when the selected parents are feasible.

4.4.3 Mutation

In this paper,two mutation operators are adopted for the OS swarm.In MSCGA,one mutation operator is selected randomly (50%) to mutate the individual in the OS swarm.

The first one is the swapping mutation.The process for swapping mutation is shown as follows.

Step 1Select two positions in P.

Step 2Swap the elements in the selected positions to generate O.

The second mutation operator is based on the neighborhood mutation method.

Step 1Select three jobs in the parent,and generate all neighborhood chromosomes.

Step 2Select the best chromosome as the current chromosome in the neighborhood chromosome.

For the MS swarm,a mutation operator is designed as follows:

Step 1Select r positions in the parent.

Step 2Change the value of each location to another machine in the corresponding collection.

4.5 Terminating criteria

If the current iteration number reaches the maximum algebra,the algorithm stops.

4.6 Framework of the MSCGA

The basic procedure of this algorithm is described as follows [26]:

Step 1Set the parameters of the MSCGA.

Step 2Initialization.Generate N+1 swarms,where there are N MS swarms and one OS swarm,and select one individual from every N+1 swarm to form one FJSP solution.

Step 3Each individual in each population is evaluated,where individuals are combined with all randomly selected partners from other populations.When Gen=1,the optimal fbestis recorded.

Step 4Is the terminating criteria satisfied? (GenmaxGen ?)

If yes,go to Step 6;if it is not,go to Step 5.

Step 5Collaborative evolution.Generate the new swarms;q is the serial number of each swarm (q=1,2,3,···,i,···,N,N+1),and initialize q=1.

Step 5.1The operator is used to generate a new population,which is set as the qth group.

Step 5.2Is qN+1?

If yes,go to Step 5.3.

If it is not,set Gen=Gen+1 and go back to Step 3;

Step 5.3Set q=q+1 and go to Step 5.1;

Step 6Output the best fitness fbestwith the solution.The flow chart is shown in Fig.2.

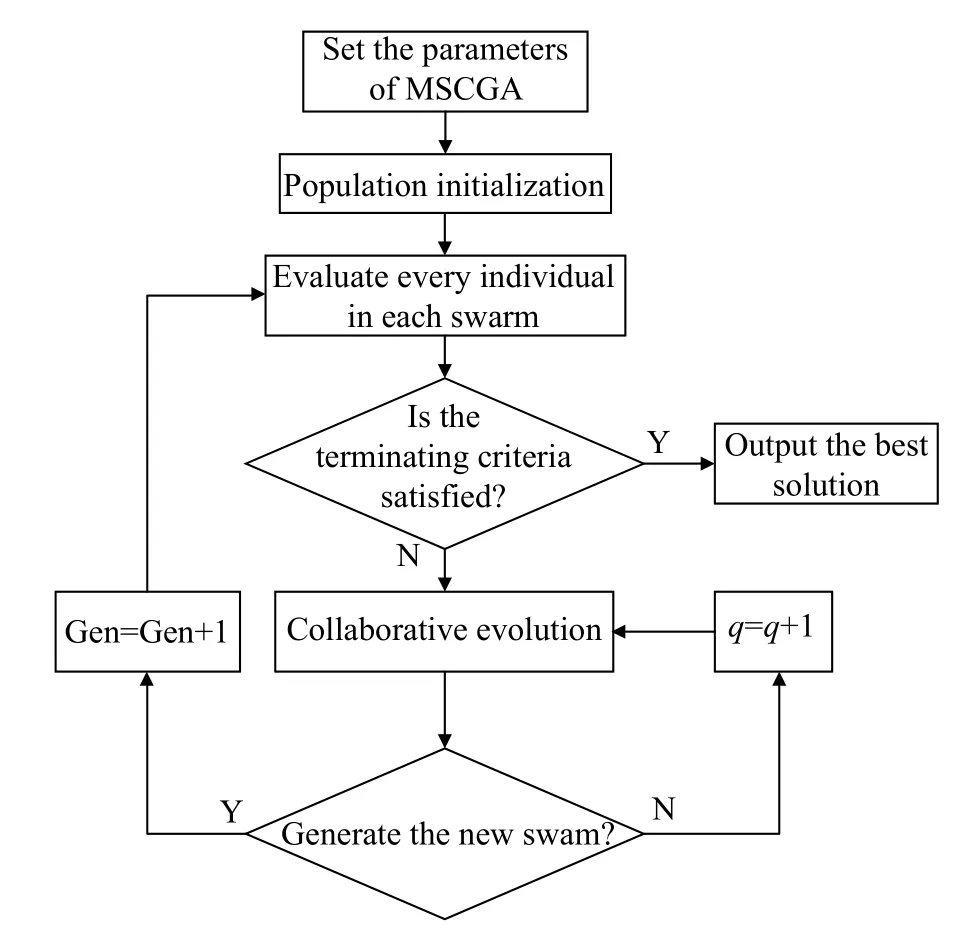
Fig.2 Framework of MSCGA

5.Experimental results

This paper selects three well-known benchmarks to evaluate the performance of the proposed MSCGA.These benchmarks include 48 open problems for the FJSP.The first instance is the MK data with 10 problems from Brandimarte [41].The second consists of data of 18 problems from Peres et al.[42].The third instance is the Fattahi data with 20 problems from Fattahi et al.[43].Comparisons between the proposed algorithm and other algorithms including three co-evolutionary algorithms are also provided.

The algorithm parameters in this paper are set as follows:the size of the population of the OS swarm Popsize1=300;the population size of the MS swarm Popsize2=300;the maximum generations maxGen=200;the crossover probabilistic of OS swarm pc1=0.8;the crossover probability of MS swarm pc2=0.8;the mutation probability of the OS swarm pm1=0.2;and the mutation probability of the MS swarm pm2=0.2.The proposed MSCGA is coded in C++and implemented on a computer with a 2.3 GHz Core (TM) i7 CPU with 16 GB RAM memory.

5.1 Results and comparison with the MK data

The MK data with 10 problems are among the most wellknown benchmarks for the FJSP.Many researchers have used this benchmark to evaluate algorithms.Table 1 shows the results of the proposed algorithm.LB is the lower bound,and UB is the upper bound.MSCGA is the proposed algorithm.LEGA2008 [12],VNSGA2019 [39],HBFOA2020 [35],PSO2020 [17],SLGA2020 [32],and two collaborative evolutionary algorithms,CCGA2010[39]and MPICA2011 [40]are selected for comparison.

Table 1 shows that the proposed MSCGA obtains thenine best results among these algorithms.This indicates that the proposed approach achieves good results for the MK data.Figs.3−5 illustrate the Gantt charts of problems MK02,MK09 and MK10 respectively.

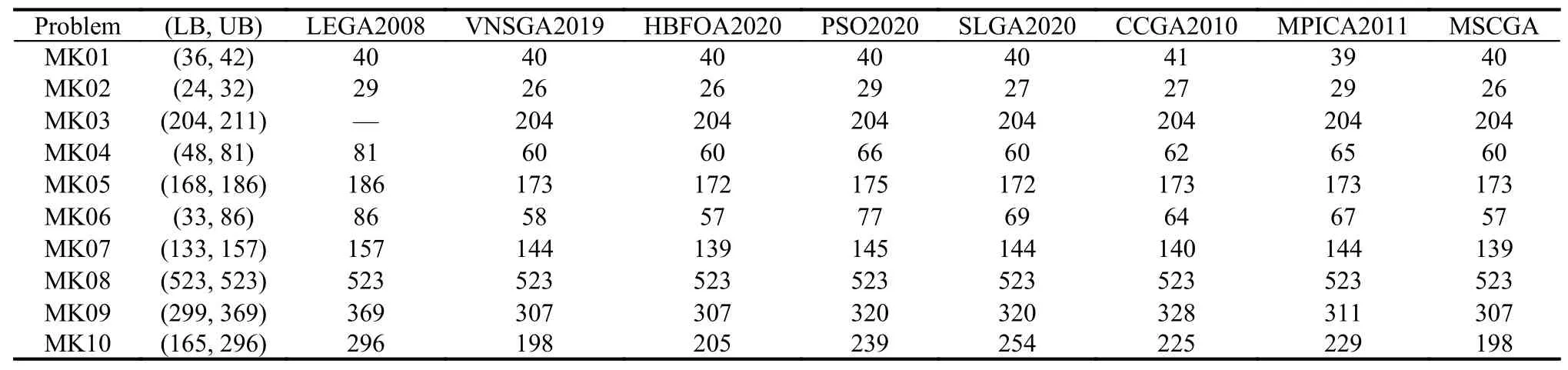
Table 1 Experimental results of MK data and comparison with other methods

Fig.3 Gantt chart of problem MK02 (Makespan=26)

Fig.4 Gantt chart of problem MK09 (Makespan=307)

Fig.5 Gantt chart of problem MK10 (Makespan=198)

5.2 Results and comparison with the Peres data

The Peres data with 18 problems were adopted from Peres et al.[42].Table 2 shows the experimental results and comparisons with the other algorithms.The MSCGA is the proposed algorithm.Integrated approach tabu search (IATS),TS,general PSO (GPSO) and discrepancy search (DS) represent the reported algorithms from Peres et al.[42],Mastrolilli et al.[15],Gao et al.[44]and Hmida et al.[45]respectively.The proposed MSCGA obtains the 13 best results among these five algorithms.The experimental results show that the number of the best results obtained by MSCGA is greater than the number obtained by the other algorithms.This means that the proposed approach can obtain increasingly better results than the other approaches.Figs.6−8 illustrate the Gantt charts of problems 01a,07a and 11a respectively.

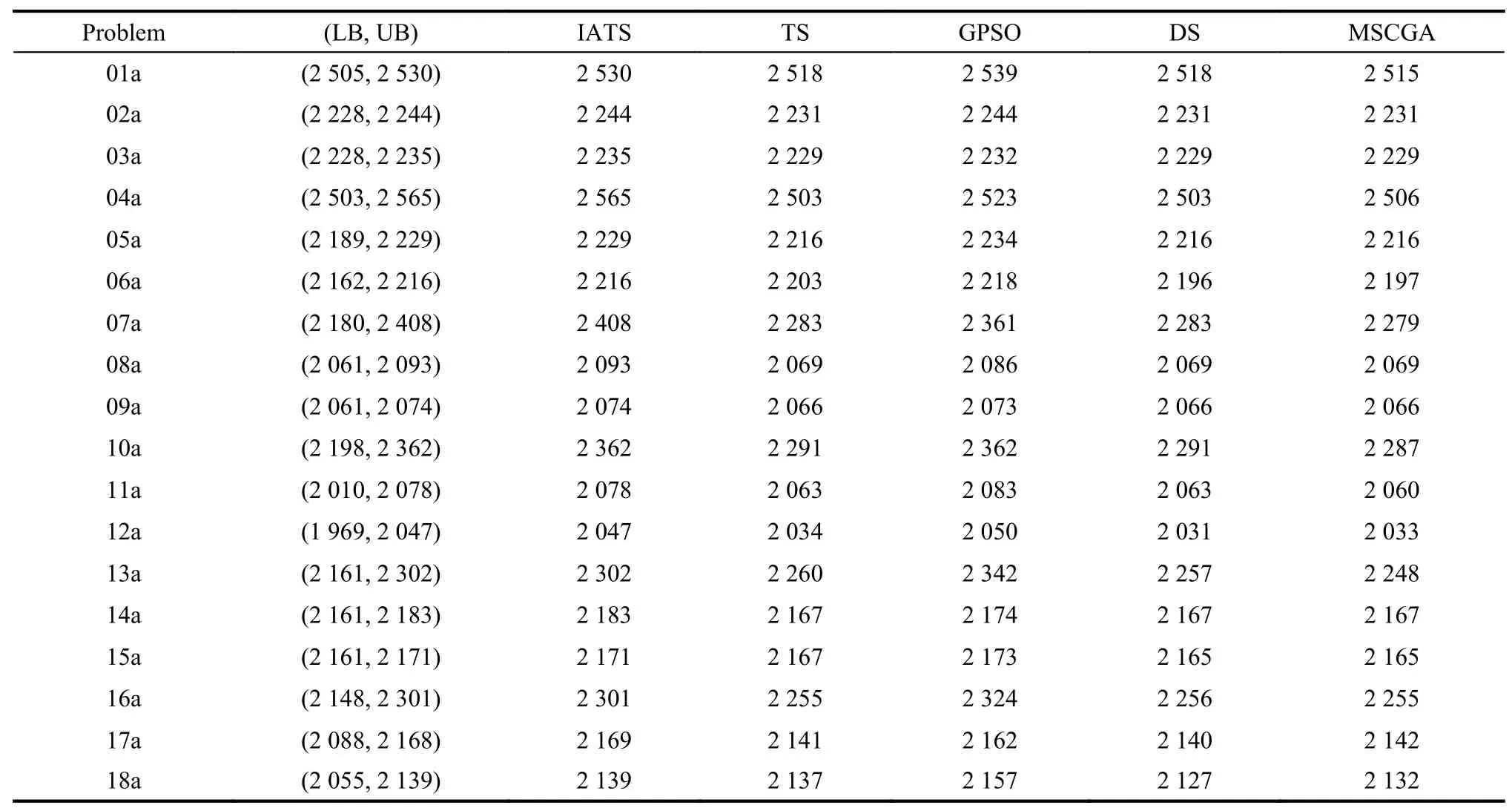
Table 2 Experimental results of Peres data and comparisons with other methods

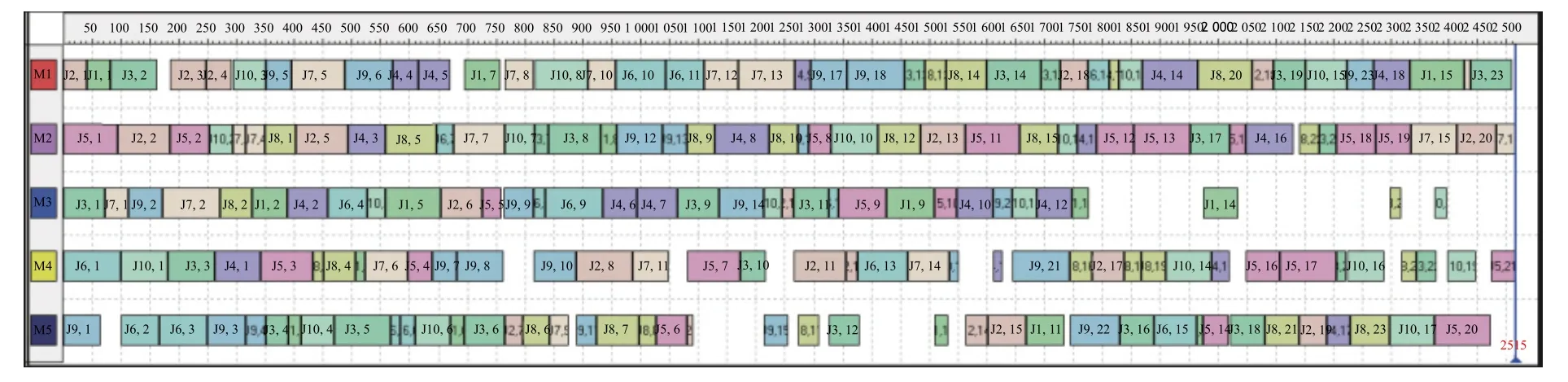
Fig.6 Gantt chart of problem 01a (Makespan=2 515)

Fig.7 Gantt chart of problem 07a (Makespan=2 279)

Fig.8 Gantt chart of problem 11a (Makespan=2 060)

5.3 Results and comparison with Fattahi data

The Fattahi data with 20 problems is adopted from Fattahi et al.[43].Table 3 shows the experimental results and comparison with the other algorithms.The MSCGA represents the proposed algorithm.The results of the artificial immune algorithm (AIA) and the hybrid harmony search (HHS) are adopted from Yuan et al.[46].The results of the second mathematical evaluation model (M2),mixed integer linear programming (MILP),modified iterated greedy (MIG) and multi-population genetic algorithm-ER (MPGA-ER) are adopted from Demir et al.[47],Birgin et al.[48],Aqel et al.[14]and Shi et al.[31]respectively.The proposed MSCGA obtains the 18 best results.The experimental results show that the number of the best results obtained by MSCGA is greater than the other algorithms except HHS,which also obtains the same number of results as the proposed algorithm.Fig.9 and Fig.10 illustrate the Gantt charts of problems MFJS09 and MFJS10 respectively.

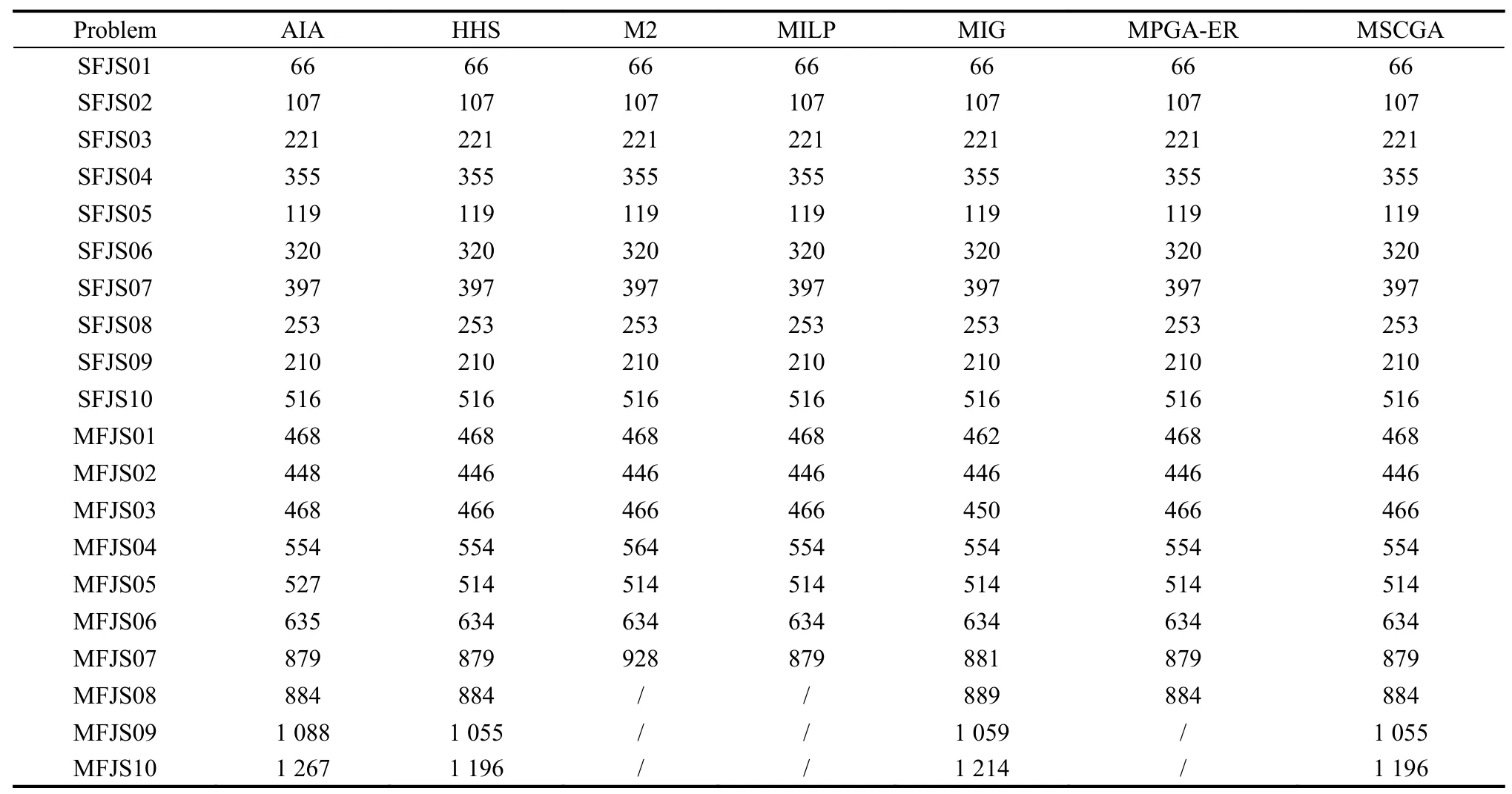
Table 3 Experimental results of Fattahi data and comparison with other methods

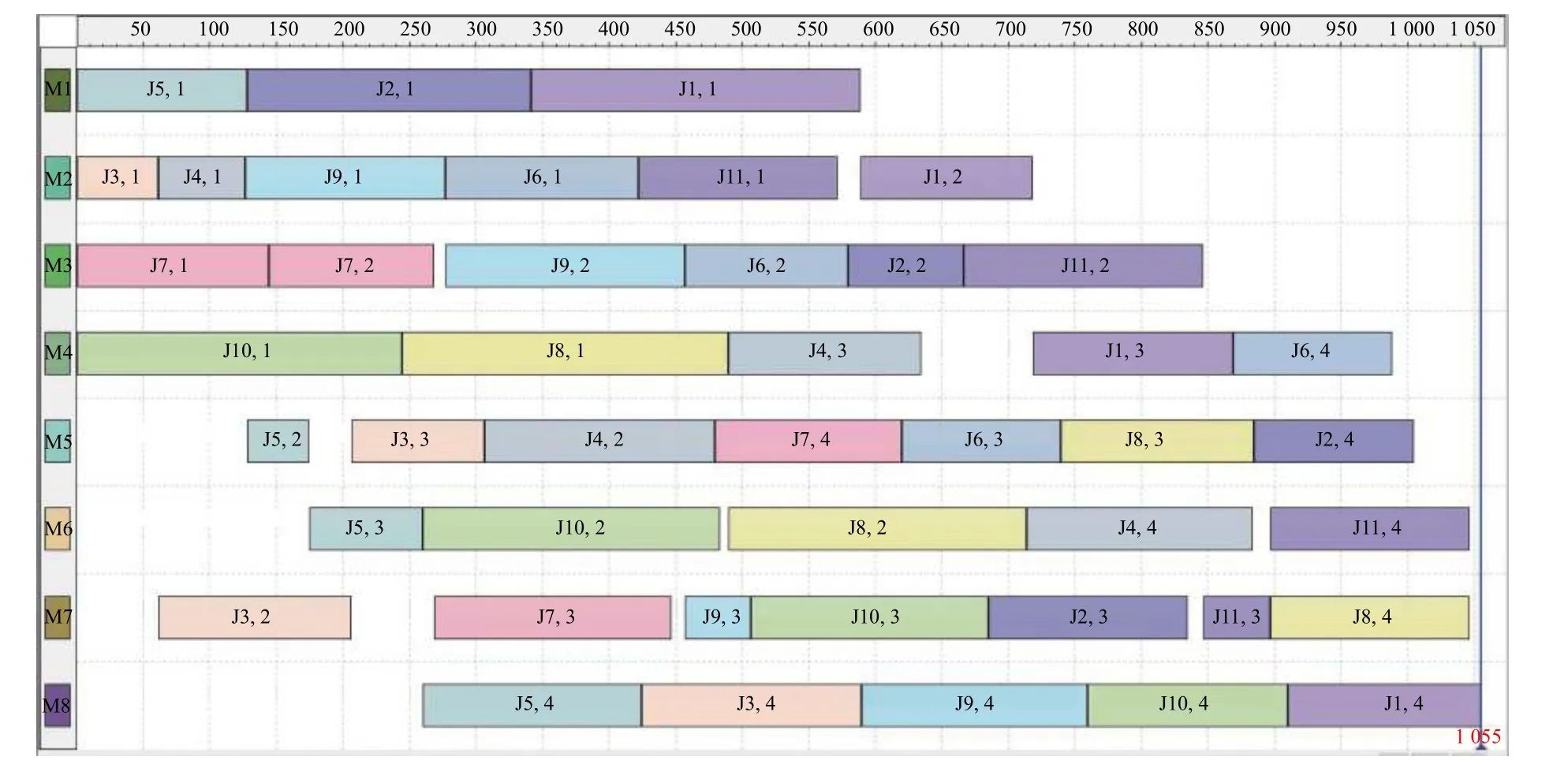
Fig.9 Gantt chart of problem MFJS09 (Makespan=1 055)

Fig.10 Gantt chart of problem MFJS10 (Makespan=1 196)

5.4 Analysis of experimental results

Table 4 gives the overall experimental results.The statistical data demonstrates that the accuracy of the solution of the proposed algorithm is obviously better than that of other algorithms.The superiority of the number of optimal solutions shows that the algorithm has a strong ability of searching for optimal solutions.At the same time,the average error reflects the stability of the algorithm.To sum up,the proposed MSCGA has certain advantages in the FJSP.

Table 4 Overall experimental results

6.Conclusions and future studies

The FJSP is an important problem in modern manufacturing systems.This paper develops an MSCGA to solve it.Moreover,some famous FJSP benchmarks are used to evaluate its effectiveness.The contributions of this research include the following:

Based on the features of the FJSP,we design all the parts of the MSCGA method.The MSCGA has been successfully used to solve the FJSP.This outcome indicates that the MSCGA is an effective method to use in the FJSP research.

The MSCGA combines the advantages of evolutionary algorithms and collaborative optimization.It provides a new way to solve problems that contain several sub-problems.

Future work will expand on the implementation and scope of the algorithm.First,to obtain more new solutions,additional effective algorithms can be combined with collaborative optimization to solve the FJSP.Second,we can extend this new way to solve the multi-objective FJSP or other scheduling problems in the manufacturing field.