A non-contact spacecraft architecture with extended stochastic state observer based control for gravity mission
LIU Sheng ,LIAO He ,XIE Jinjin ,XU Yufei ,XU Yi ,TANG Zhongxin ,and YAO Chuang
1.School of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China;2.School of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;3.Research Center,Shanghai Institute of Satellite Engineering,Shanghai 201109,China
Abstract: A novel non-contact spacecraft architecture with the extended stochastic state observer for disturbance rejection control of the gravity satellite is proposed.First,the precise linear driving non-contact voice-coil actuators are used to separate the whole spacecraft into the non-contact payload module and the service module,and to build an ideal loop with precise dynamics for disturbance rejection control of the payload module.Second,an extended stochastic state observer is enveloped to construct the overall nonlinear external terms and the internal coupled terms of the payload module,enabling the controller design of the payload module turned into the linear form with simple bandwidth-parameterization tuning in the frequency domain.As a result,the disturbance rejection control of the payload module can be explicitly achieved in a timely manner without complicated tuning in actual implementation.Finally,an extensive numerical simulation is conducted to validate the feasibility and effectiveness of the proposed approach.
Keywords:non-contact spacecraft architecture,extended stochastic state observer,disturbance rejection control,non-contact voice-coil actuators,bandwidth-parameterization tuning.
1.Introduction
The ultra-sensitive electrostatic accelerometer (UEA) has been deeply linked to the gravity missions [1].In each UEA configuration,an internal free-falling proof-mass is electro-statically suspended at the center of mass (COM)of the gravity satellite by means of voltages applied to the electrodes around the vacuum chamber to measure the residual non-gravitational acceleration.Therefore,the global,regular and uniform gravity fields of the Earth,such as gravitational coefficients and geoid heights can be recovered [2].
There are mainly two alternative concepts proposed to recover the gravity field in actual application.The first concept is the gravitational gradient mode,in which the gradient tensor is used to elucidate the effect of the smallscale feature of the steady gravity field based on the classical differential approach.The satellite-to-satellite tracking mode has been proposed as the second mode.The time-varying gravity field can be retrieved from the formation fluctuation of the range and the non-gravitational acceleration.The gravitational gradient mode and the satellite-to-satellite tracking mode are irreplaceable and complementary for each other,which can be fused together to recover the high-quality gravity field [3,4].
Since the dynamic range of the UEA is related to the resolution of the gravity field,the all-propulsion disturbance rejection control has been proposed to ensure the observation accuracy of the UEA by micro-thrusters in previous researches.Therefore,two control issues have to be considered.First,the controller should be carefully designed in the frequency domain compatible with the resolution of the gravity field.Second,the controller must be robust against the thruster-to-spacecraft dynamic uncertainties aggravated by micro-thrusters [5−8].
An effective frequency domain approach with transfer function analysis based on the proportional derivative control algorithm has been proposed to yield reliable performance due to its simplicity [9].However,the satisfactory performance cannot be obtained due to the inaccurate expression of the uncertainties.Modern control theories,such as theH∞technique and the quantitative feedback theory have been proposed for robust stability in the frequency domain with unstructured uncertainties.The non-smooth optimization based on theH∞technique guarantees the structured parametric controller tuning for disturbance rejection control through designing the frequency domain loop shape [10].The quantitative feedback theory provides an intuitive tuning approach to trade off the control performance and the spectral densities constraints of the uncertainties through balancing the available design margins among different specifications[11].However,it is hard to apply in application directly due to its complex computation process.Disturbance-observer based control becomes quite attractive due to its uniqueness in concept,simplicity and superiority in actual implementation [12,13].The intuitive idea of the disturbance-observer based control is to estimate the internal and external disturbance from observable variables.Therefore,the predictive disturbance in the frequency domain can be gradually rejected [14−18].Nevertheless,advantages of the controllers cannot be exploited optimally if the disturbance-observer based control is applied directly because the target design of the spectral characteristics of the neglected thruster-to-spacecraft dynamics is lacked.
A novel non-contact spacecraft (NCS) architecture which is separated into the payload module (PM) and the service module (SM) within an air-gap of several centimeters relies upon the non-contact voice-coil actuator(NCVCA) is proposed to improve the disturbance rejection control performance for the gravity mission in this paper.The NCVCA adopted here is a linear motor with precise electrical driving.Therefore,it can be used to provide precise accuracy,fast response and broaden bandwidth force for disturbance rejection control of the PM compared with the micro-thruster adopted in previous researches [19].Meanwhile,the SM only needs to track the PM roughly to avoid collision within the air-gap through a series of low thrusters.Apparently,this kind of architecture brings a great advantage for disturbanceobserver based control of the PM since the precise dynamics and accurate driving are ensured through replacing the micro-thruster with the NCVCA.
The rest of this paper is organized as follows.The NCS architecture and the control hierarchical control architecture are given in Section 2.Next,Section 3 details the whole dynamics modeling and the controller design of the subject NCS.Section 4 details the numerical simulation to demonstrate the feasibility and effectiveness of the proposed approach.Finally,Section 5 concludes the paper.
2.NCS architecture
2.1 Structure design
The first concept of the NCS can be dated back to Nelson’s disturbance-free payload [20],which has been verified successfully to achieve perfect vibration isolation.The key instrument is the NCVCA which is used to separate the whole spacecraft into two non-contact modules and to provide active control input [21,22].
Inspired by the concept of the disturbance-free payload,the NCS structure as shown in Fig.1 is proposed to be applied in the gravity mission to improve the disturbance rejection control performance in this paper.
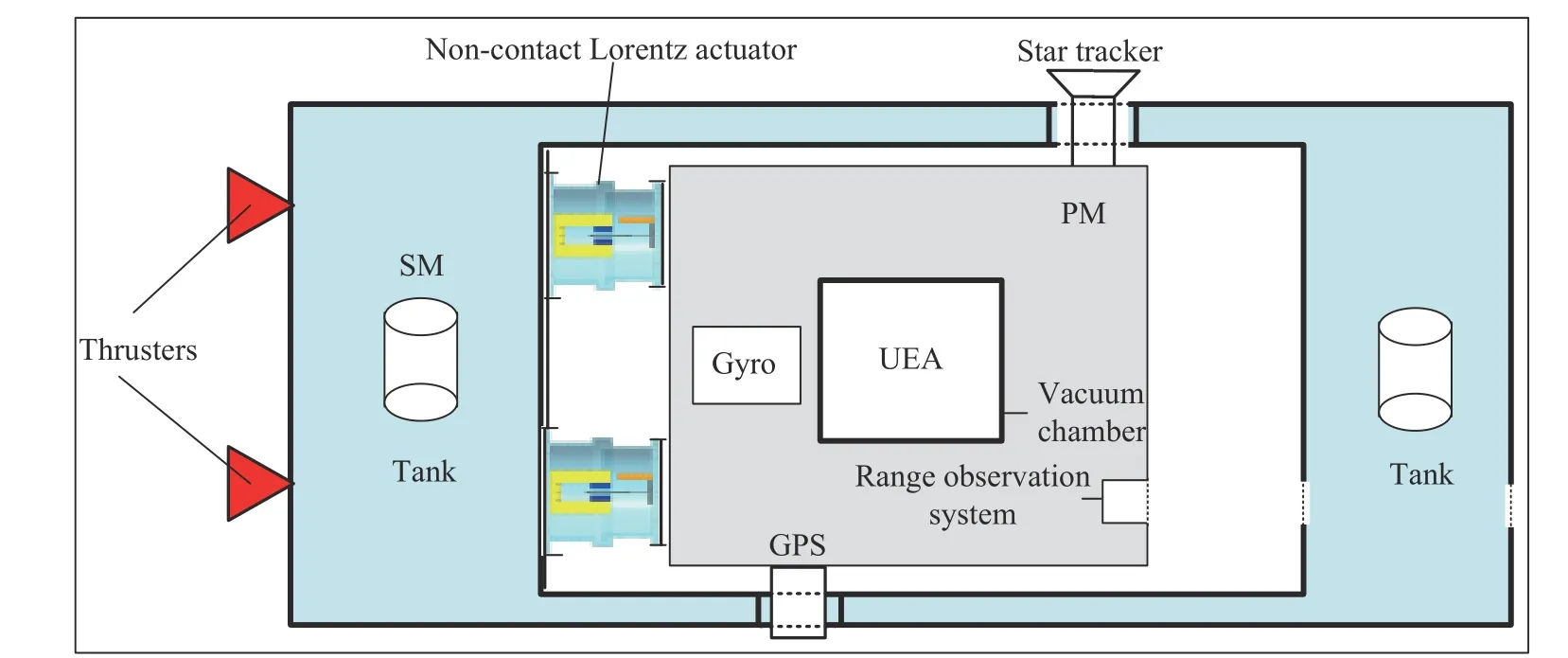
Fig.1 Structure of the subject NCS
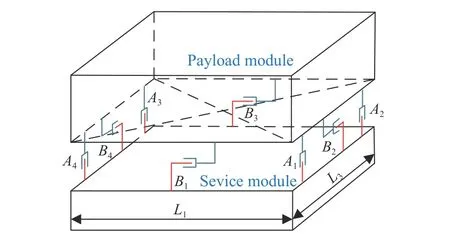
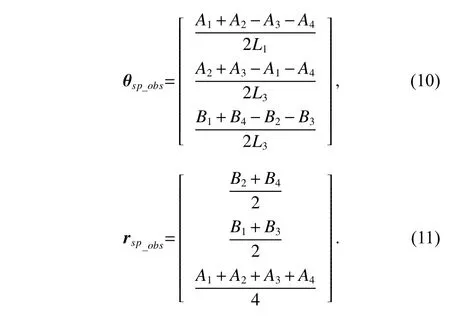
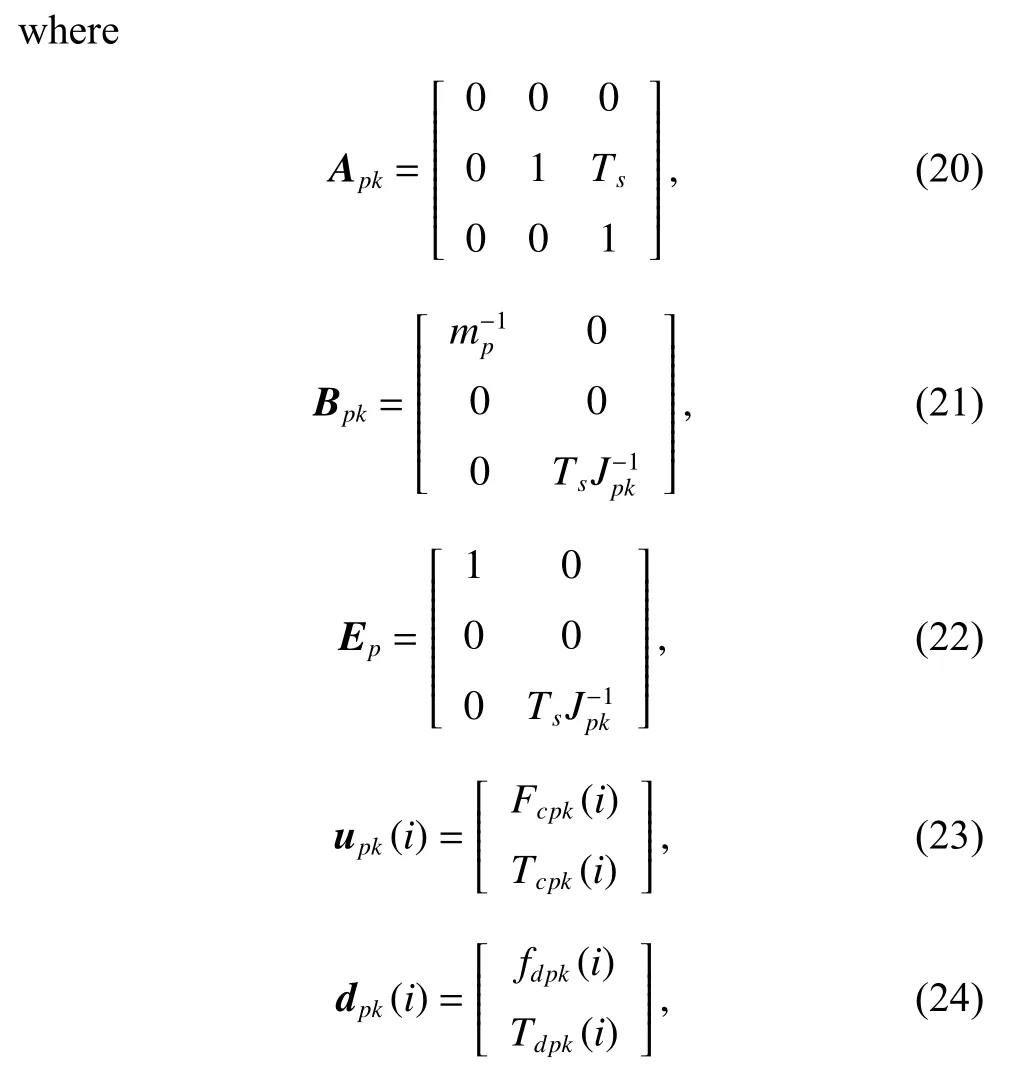
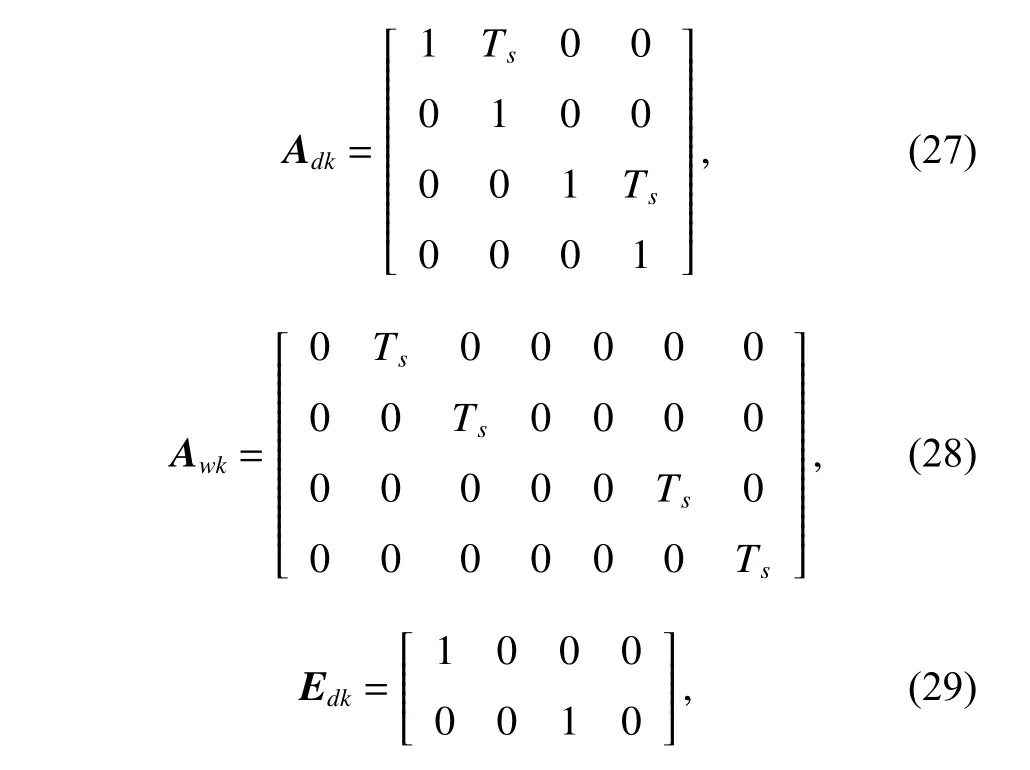
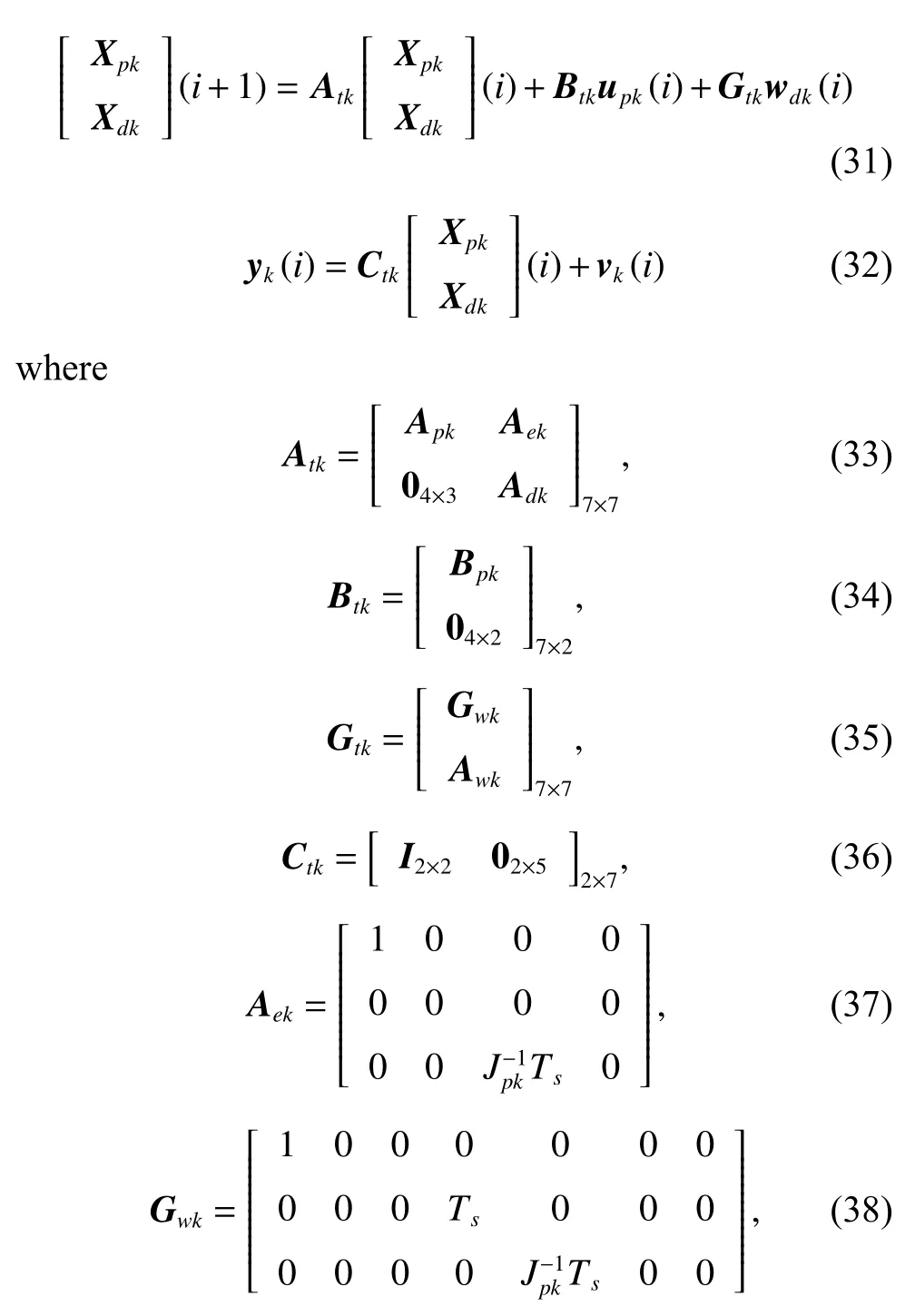
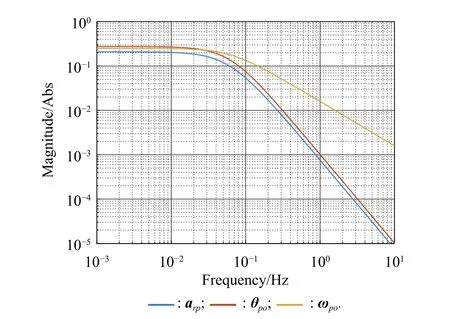
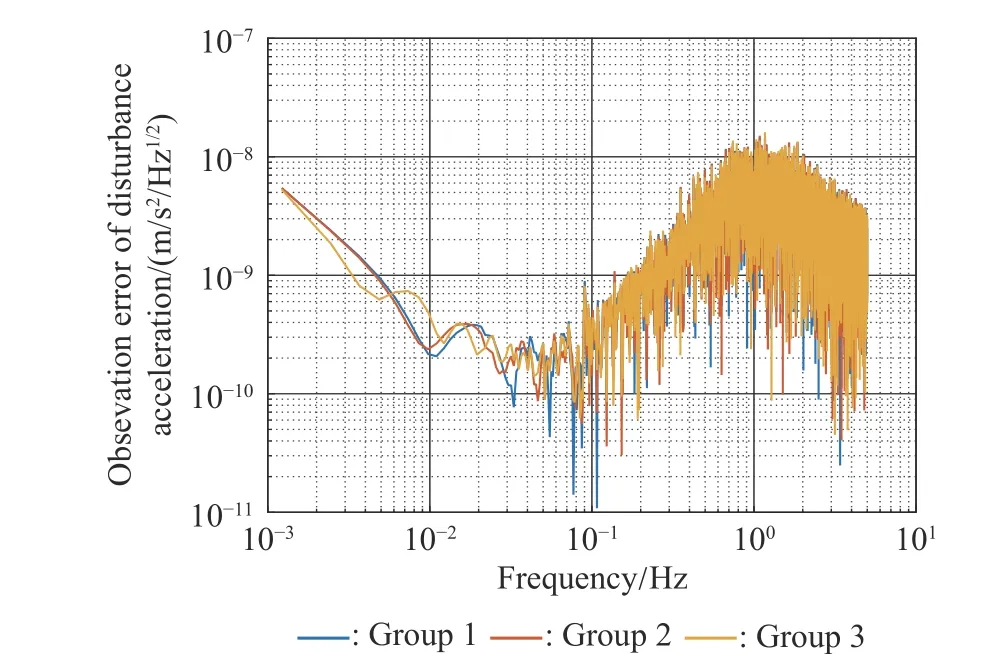
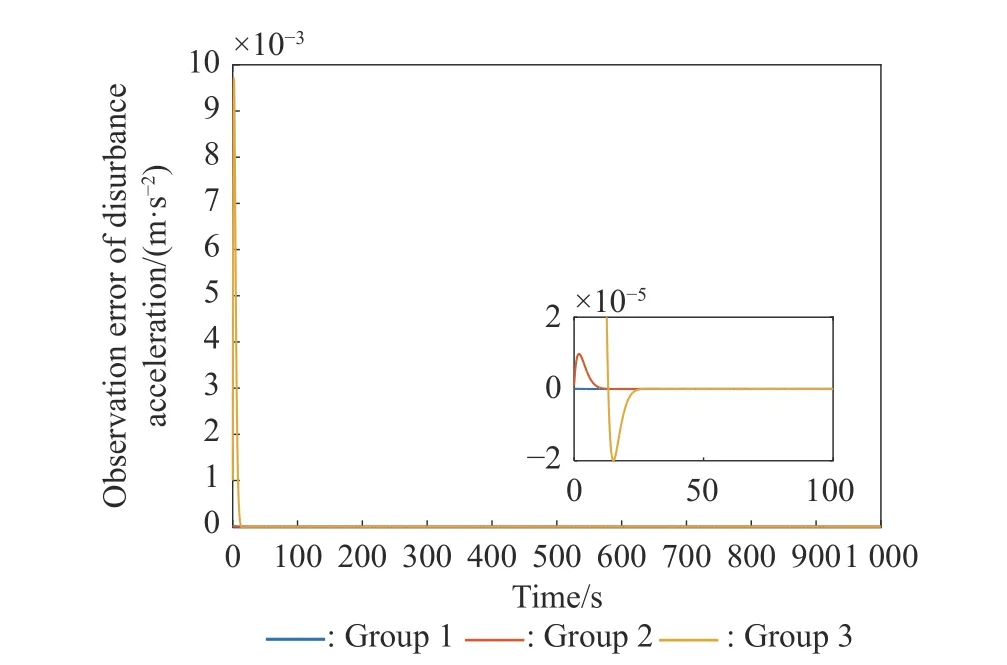
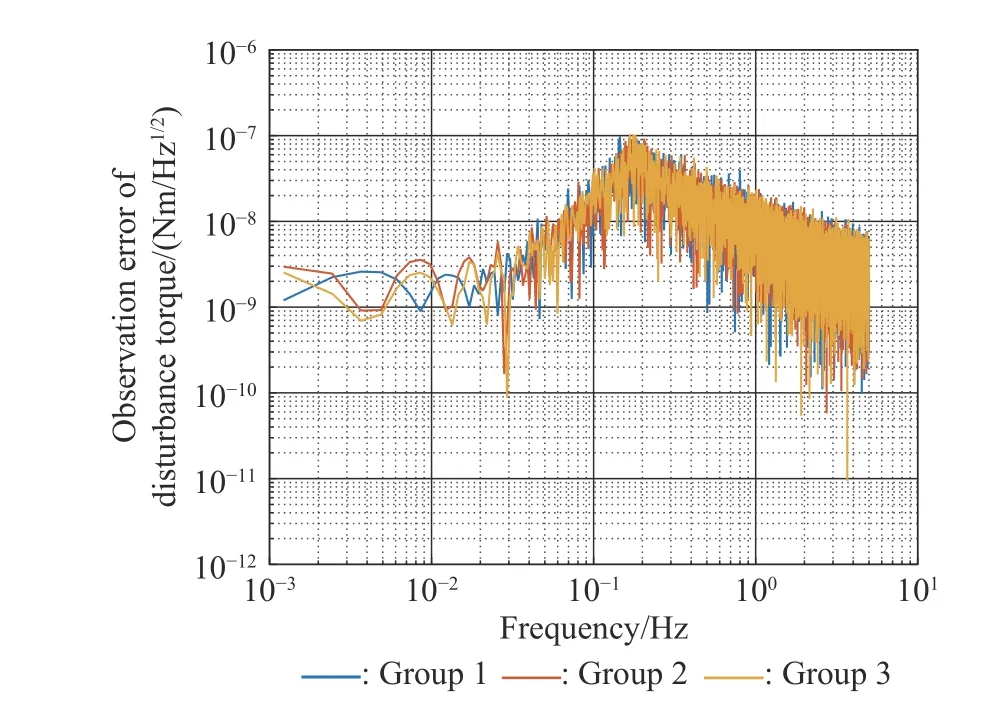
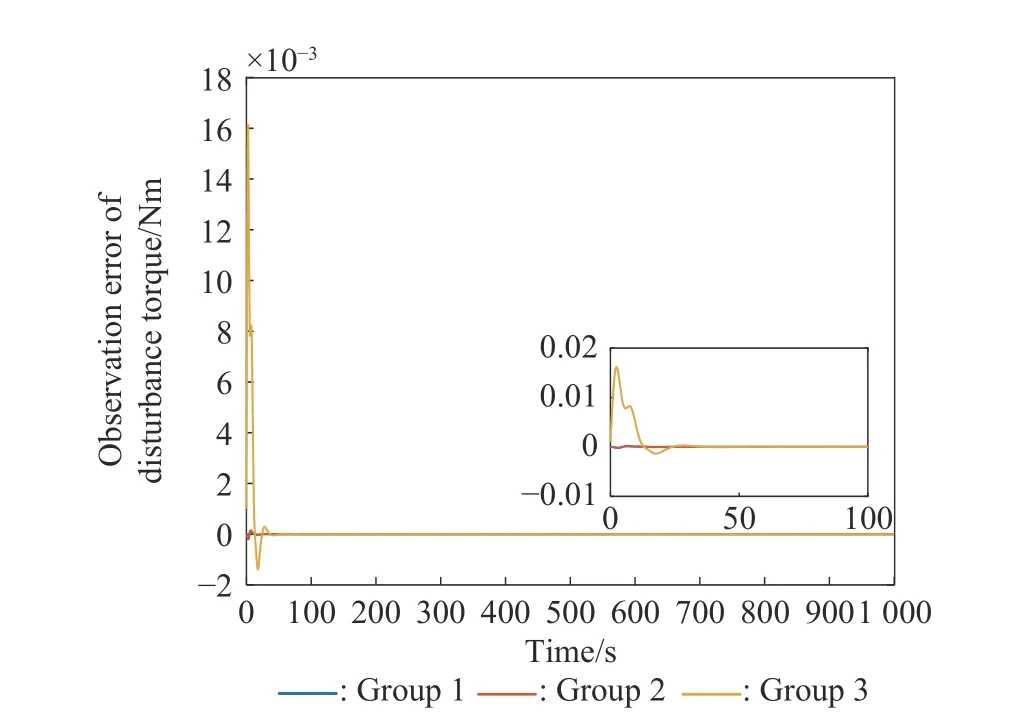
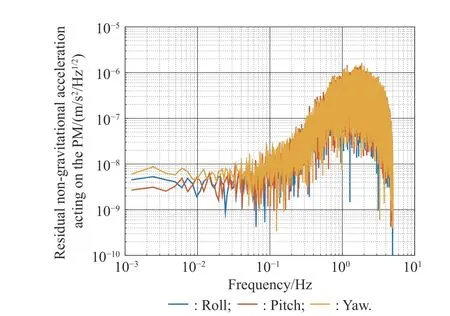
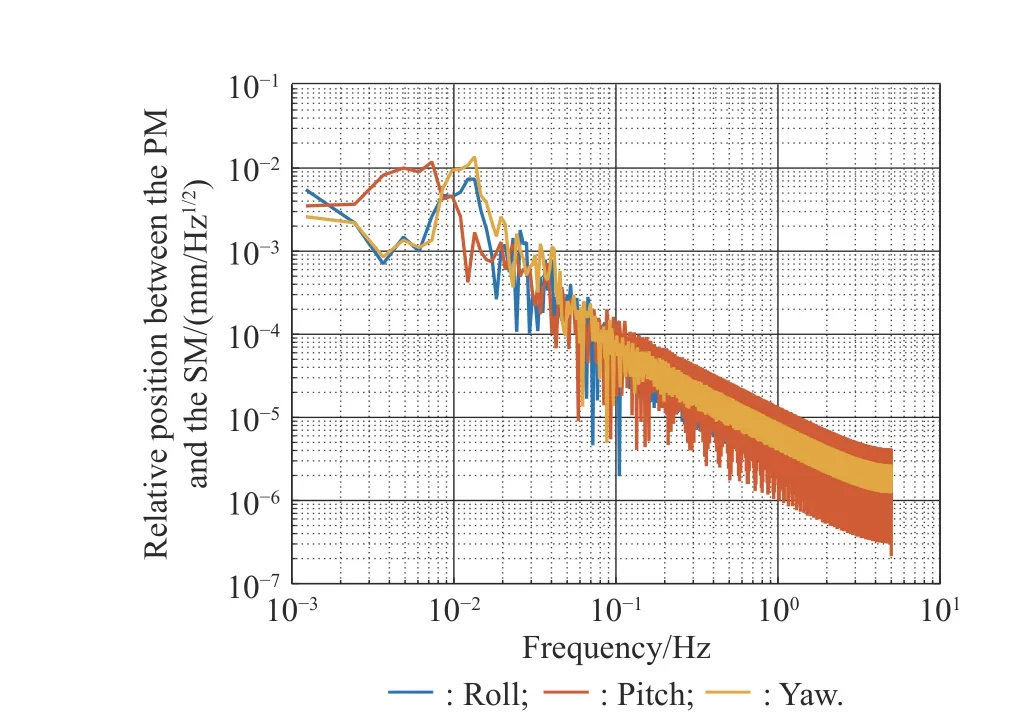
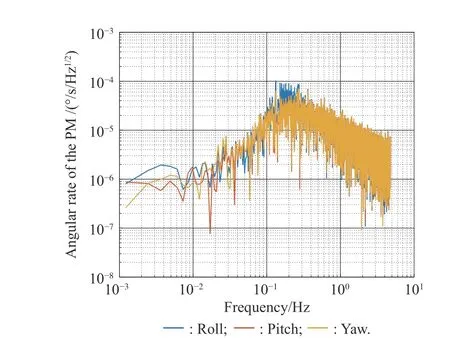
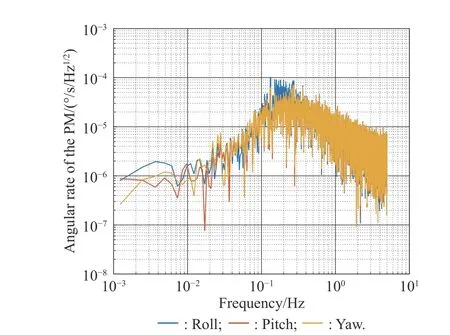
To satisfy the requirement of the gravity mission,the disturbance rejection control should be compatible with the resolution of the gravity field recovery.It is partitioned into the low-frequency bandξ0={f With the continuous development of the research,the intensity of the permanent magnet of the NCVCA within an air-gap of several centimeters can be processed as a homogeneous field,suggesting that the commanded input with fast response and broad bandwidth can be actuated while the accuracy is the same as the micro-thruster due to its precise linear driving current.According to the experimental tests in our laboratory,the noise spectral density of the NCVCASt0can be achieved as 2 μN/Hz1/2.The evaluated equation of the NCVCA is shown as follows [23]: whereSt(f) denotes the mininal noise spectral density across the mid-frequency bandξ2,andfl≤fmaxis within the mid-frequency bandξ2. This result is sufficient enough to obtain a good performance for disturbance rejection control of the PM compared with the micro thruster equipped in the gravity field and steady-state ocean circulation explorer (GOCE)and the next generation gravity mission [24]. In order to discuss the behavior of the subject NCS,the J2000.0 equatorial frame is defined as the inertial frame(IF).The tracking coordinate system of the disturbance rejection control is a Cartesian right-handed frame fixed to the local orbit frame (LORF) of the PM,in which the origin is fixed at the mass center of the PM.The body frame (BF) of the PM and the BF of the BM are defined as the Cartesian right-handed frames fixed to the mass distribution and geometry,respectively. The UEA,the star tracker and the GPS equipped within the PM are used to provide attitude pointing observations for disturbance rejection control of the PM.Meanwhile,in order to provide precise input for disturbance rejection control of the PM in six degrees of freedom,a symmetrical configuration with the eight NCVCAs as shown in Fig.2 is designed carefully to guarantee both accuracy and redundancy.Therefore,the minimum norm solution can be hired to allocate each NCVCA to provide precise input,which has been proven as the globally optimal solution [25]. Fig.2 Symmetrical configuration with eight NCVCAs This kind of symmetrical configuration also brings convenience for the relative observation between the PM and the SM.Since the relative position detectors like the laser interferometers can be equipped with the eight NCVCAs,the relative position and attitude observations can thus be obtained as follows according to the geometric definition. Defining the relative position observation and the relative attitude observation between the SM and the PM asrsp_obs=[rsp_obsxrsp_obsyrsp_obsz]T,θsp_obs=[θsp_obsxθsp_obsy θsp_obsz]T.Then each position detector can be written as whereA1,A2,A3,A4,B1,B2,B3,B4denote the observable distances of each splitting permanent magnet and current,respectively;L1andL3denote the fixed dimension along pitch and yaw axes which can be precisely calibrated,respectively. Therefore,the relative position and attitude observations for collaborative control of the SM relative to the PM can be yielded: Since the requirement of the collaborative control of the SM is not as strict as the PM,the relative velocity and angular rate observations can be obtained from the differential observations of the relative position and attitude. Finally,in order to avoid the issues due to cables,the wireless technologies which has been proven to be feasible during the in-flight phase in recent years are adopted to provide information communication and power supply between the PM and the SM. The NCVCA and the PM constitute an ideal feedback loop with precise dynamics through non-contact design.Therefore,the total disturbance acting on the PM is comprised of the nonlinear external terms and the internal coupled terms.Theoretically,it can be expressed as a nonlinear function of the orbit and attitude motion according to the previous researches on the experimental data about the disturbance spectral densities from the direct current (DC) to the Nyquist frequency at the low-orbit altitude [26].Nevertheless,the controller would suffer the problem with high gain and multi-parameters tuning if the nonlinear extended state observer is applied directly to estimate the disturbance. Inspired by the linear signal process approach of the second-order stochastic dynamics,since it can be used to model a very wide range of signals,an extended stochastic state observer-based control is proposed for disturbance rejection control of the PM.This kind of design brings great convenience for controller design,suggesting that the nonlinear external terms and the internal coupled terms can be transferred into a linear form through defining them as an extended stochastic state.Therefore,the mature theory of the linear disturbance-observer based control with bandwidth-parameterization in the frequency domain can be applied simply.As a result,the disturbance rejection control of the PM can be explicitly achieved in a timely manner without complicated tuning in actual implementation. Meanwhile,it can be seen easily that the SM adopted here is used to provide support for the PM,the control requirement of the SM is only needed to avoid collision by tracking the PM within the air-gap of the NCVCA.Therefore,the proportion and differentiation (PD) control law with feedback linearity correction by a series of low thrusters is considered in this paper. As stated above,the hierarchical control architecture of the subject NCS can be detailed in Fig.3. Fig.3 Hierarchical control architecture of the NCS As stated in the above-mentioned section,the whole control of the subject NCS is comprised of the precise disturbance rejection control of the PM and the coarse collaboration of the SM.Therefore,the extended stochastic observer based control for the PM consisting of controllable dynamics,extended observer design,control law and closed-loop analysis is descripted in detail at first.Then the collaborative control for the SM with PD-based feedback linearity correction is introduced. Defining the position and the velocity of the PM in the IF asrpandvprespectively,the inertial COM equations of the PM can be expressed as wheregpdenotes the gravitational acceleration,Cpidenotes the rotation matrix of the BF of the PM relative to the IF,arpdenotes the residual non-gravitational acceleration,fdpdenotes the environment acceleration acting on the PM,mpdenotes the mass of the PM andFcpdenotes the drag free control force. Defining the Euler angle and the angular rate of the BF of the PM relative to the LORF of the PM asθpoandωporespectively,the attitude equations of the PM can be expressed as whereJpdenotes the inertial matrix of the PM,Tcpdenotes the attitude control torque,Tdpdenotes the disturbance torque acting on the PM,τdpdenotes the environment torque,Cpodenotes the rotation matrix of the BF of the PM relative to the LORF of the PM,× denotes the difference multiplication operactor,andωoidenotes the angular rate of the LORF of the PM relative to the IF. Since the requirement of the disturbance rejection control is to ensure the orbit of the PM aligned with an ideal Kepler orbit and the BF of the PM aligned with the LORF of the PM,the following zero-tracking performance should be achieved: Defining the state variation asXpk=[arkθpokωpok]T(k=roll,pitch,yaw),the discrete form of the generic single-axis controllable dynamics of the PM can be written as follows according to the inertial COM and attitude equations of the PM according to (12)−(17). whereTsdenotes the designed time step. Since the commanded force can be actuated precisely by the NCVCA,the main problem is to estimate the total disturbance acting on the PM according to (19).In this paper,a linear extended state observer driven by bounded second-order stochastic dynamics is used to construct the overall explicit model.Therefore,the extended state equations of the total disturbance acting on the PM can be written as whereXdkdenotes the extended state variation sized as 4×1,wdkdenotes the driving noise sized as 7×1,where no causal relation exists,the notations in the above-mentioned equations are given as follows: Substituting (25) and (26) into the controllable dynamics of the PM and combining the observation equation,the entire disturbance rejection control model can thus be obtained as whereykdenotes the observation of the state variation andvkdenotes the observation error. It can be easily found that the propagation of the state variation is driven by the driving noisewdkof the extended state equations.Therefore,the entire disturbance rejection control converts into a linear state observer through solving the simple constraint of the noise estimator in real-time.Apparently,the only way is to correlate the driving noisewdkto the errorek=yk−Xpk.The sufficient and necessary condition for guaranteeing a bounded error is to construct a static noise estimator gain through linear time-invariant correlation as follows: whereLk(i)=[l1l2l3l4l5l6l7]Tdenotes the noise estimator gain. Therefore,the noise estimator gain can be determined as follows through bandwidth-parameterization in the frequency domain. whereω0denotes the observer bandwidth. Since the noise estimator gain can be tuned properly through assigning the closed-loop eigenvalues in the frequency domain as shown above,the control law compatible with the resolution of the gravity field can thus be given by wherek1andk2denote the PD coefficients,which can be designed as whereωcdenotes the closed-loop bandwidth of the controller,Vais a constant,andVa∈[0.1,0.2]. Apparently,it can be seen that the uncertainties terms withinBtk upkaccording to (46) would affect the control accuracy even if the above-mentioned algorithm is exerted for the previous all-propulsion disturbance rejection control.Since the NCVCA is used in an ideal loop with precise dynamics of the PM and to provide a high-quality actuation for the disturbance rejection control of the PM,thus compared with the previous all-propulsion approach,a better performance can be guaranteed through simple bandwidth-parameterization as stated above. As stated above,the extended stochastic state observer according to (40) plays an important role on the closedloop disturbance rejection control.Since the driving noise is assumed to be independent with the state variation,the input-output closed-loop transfer matrixMand the sensitivity matrixScan be expressed as wherezdenotesztransformation. According to the small gain theorem,the following inequalities can be guaranteed apparently through the abovementioned bandwidth-parameterization with reasonable eigenvalues tuning in the frequency domain.Therefore,the closed-loop stability can be ensured. Since the requirement of the collaborative control of the SM is to track the PM within the air-gap of the NCVCA roughly,the control scheme is to ensure the BF of the SM aligned with the BF of the PM for avoiding collision through a series of lower thrusters. Defining the relative position and the velocity between the PM and the SM asrspandvsprespectively,the translational equations of the SM relative to the PM can be expressed as wheremsdenotes the mass of the SM,Fcsdenotes the collaborative control force,Csidenotes the rotation matrix of the BF of the SM relative to the IF,fggidenotes the acceleration induced by gravitational gradient in the IF,fdsdenotes the environment acceleration acting on the SM,Cspdenotes the rotation matrix of the BF of the SM relative to the BF of the PM,andωsidenotes the angular rate of the SM relative to the IF. Meanwhile,defining the relative attitude and the angular rate of the SM relative to the PM asθspandωsp,the rotational equations of the SM can be expressed as whereJsdenotes the inertial matrix of the SM,Tcsandτdsdenote the collaborative control torque and the environment torque acting on the SM,respectively. The notation ofωsiis given as follows: Since the requirement of the collaborative of the SM is not as strict as the PM,a PD-based feedback linearity correction is considered as follows: whereKtrandKtvdenote the PD coefficients of the translational collaborative control,respectively;KraandKrrdenote the PD coefficients of the rotational collaborative control,respectively;andΔtrandΔrodenote the terms of the feedback linearity correction,respectively. Constructing a state vectorxtr=[rspvsp]T,andxtr=0 represents the equilibrium of the translational collaborative control of the SM.Considering the following candidate Lyapunov function: whereVtr(xtr) denotes positive definite obviously,andVtr(xtr)=0.Furthermore,the derivative ofVtr(xtr) is Meanwhile,constructing a state vectorxro=[θspωsp]T,andxro=0 represents the equilibrium of the rotational collaborative control of the SM.Considering the following candidate Lyapunov function: Clearly,it is analogous to the stability analysis of the translational collaborative control,which leads to Therefore,it can be concluded that the closed-loop of the translational and rotational collaborative control of the SM is globally asymptotically stable. A case study of the NCS architecture with the extended stochastic state observer based control is presented to illustrate the feasibility and effectiveness of the proposed algorithm in this section. Firstly,suppose that the NCS flies in a circular,duskdawn sun-synchronized orbit at an altitude of 250 km.The subject parameters of the orbital environment and the NCS in the numerical simulation are detailed in Table 1. Table 1 Parameters of the orbital environment and the non-contact spacecraft As stated above,the parameters of the observable sensors and actuators in the numerical simulation are detailed in Table 2. Table 2 Parameters of the observable sensors and actuators As stated in Section 3,the noise estimator gain is related to the observer bandwidth.The response speed would be faster if the observer bandwidth is designed as a higher value.However,the excessive noise would be implanted into the estimating process.In order to be compatible with the resolution of the gravity field,the estimated accuracy within the mid-frequency band should be vitally ensured.Therefore,the observer bandwidth is selected as the cutoff frequency of the mid-frequency band.Substituting the numeric value into (50),the closed-loop stability can be guaranteed apparently.The simulated result is shown in Fig.4. Fig.4 Simulated result of the closed-loop stability As stated in Section 3,the extended stochastic state observer is used to construct the overall explicit model of the disturbance accelerations and the disturbance torques.Nevertheless,the initial value of the extended stochastic state is unknown in actual application.Therefore,three groups of the initial value are selected to analyze the estimation efficiency,i.e.,Xdk=04×1for Group 1,Xdk=[1×10−61×10−61×10−61×10−6]Tfor Group 2,andXdk=[1×10−31×10−31×10−31×10−3]Tfor Group 3.The simulated time is 1 000 s and the simulated time step is 0.1 s.The simulated results of the observation error of the disturbance acceleration and the disturbance torque along the roll axis are shown in Figs.5−8. Fig.5 Observation error of disturbance acceleration along roll axis of PM in the frequency domain Fig.6 Observation error of disturbance acceleration along roll axis of PM in the time domain Fig.7 Observation error of disturbance torque along roll axis of PM in the frequency domain Fig.8 Observation error of disturbance torque along roll axis of PM in the time domain It can be founded that the initial value of the extended stochastic state is related to the convergence velocity,but irrelevant to the estimation accuracy according to the simulated results in the time and frequency domain as shown in Figs.5−8.The main reason is that the smaller deviation between the real value of the disturbance and the initial value of the extended stochastic state is more beneficial to the convergence velocity.Although the environment disturbance and the coupled term as shown in(17) of the PM are unknown,they are commonly small values.Therefore,the initial value only needs to be set as 0,both the convergence velocity and the estimated accuracy can be ensured.The same conclusion can be founded for the other two axes. Meanwhile,Fig.5 and Fig.7 show that the spectral density of the observation error for disturbance acceleration can be achieved below 1×10−9m/s2/Hz1/2and the spectral density of the observation error for the disturbance torque can be achieved below 5×10−7Nm/Hz1/2in the mid-frequency band.Compared with the accuracy of the NCVCA refering to (1),the estimated efficiency is accurate enough for disturbance rejection control compatible with the resolution of the gravity field. As stated above,the proposed extended stochastic state observer is feasible and effective to describe the disturbance dynamics of the PM while the precise dynamics of the PM is built through the subject NCS architecture in this paper.Moreover,compared with the tuning technique of the initial value and the initial covariance matrix of the Kalman filtering,this kind of design leads to more simple and reliable selection of the initial value. The simulation results of the proposed design of the disturbance rejection control with the extended stochastic state observer are shown in Figs.9−16. Fig.9 Residual non-gravitational acceleration acting on the PM in the frequency domain Fig.10 Relative position between the PM and the SM in the frequency domain Fig.11 Euler angle of PM in the frequency domain Fig.12 Angular rate of PM in the frequency domain Fig.13 Relative Euler angle between the PM and the SM in the frequency domain Fig.14 Relative angular rate between the PM and the SM in the frequency domain Fig.15 Driving force of PM Fig.16 Control force of SM Fig.9 shows residual non-gravitational acceleration acting on PM compatible with the resolution of the gravity field can be achieved as the order of 10−8m/s2/Hz1/2.Fig.11 shows the Euler angle of the PM compatible with the resolution of the gravity field can be achieved as the order of 10−4°/Hz1/2.Fig.12 shows the angular rate of the PM compatible with the resolution of the gravity field can be achieved as 10−5°/s/Hz1/2.The simulated accuracy for disturbance rejection control is meaningful as it can be helpful for both the gravitational mode and the next generation satellite-to-satellite tracking mode with laser ranging. Fig.10 shows the relative position between the PM and the SM can be achieved as 0.02 mm/Hz1/2.Fig.13 shows the relative Euler angle between the PM and the SM can be achieved as 0.01°/Hz1/2.Fig.14 shows the relative angular rate between the PM and the SM can be achieved as 0.005°/s/Hz1/2.Clearly,the collaborative control of the SM is effective to track the PM within the air-gap of the NCVCA without collision. Fig.15 shows the NCVCA can be used to guarantee the performance of the disturbance rejection control of the PM.Fig.16 shows the lower thruster is sufficient to ensure the collaborative control of the SM,indicating that this kind of NCS design can be used to reduce the hardware requirement of the time-variant thruster. According to the above extensive numerical simulation,it is sufficient to verify that the proposed approach can achieve a good performance in a timely manner without complicated tuning with fewer hardware requirements of the time-variant thruster. An NCS architecture and its disturbance rejection control with the extended stochastic state observer by taking advantages of the linear driving NCVCA is proposed for gravity mission in this paper.The proposed NCS can be used to build a precise dynamics for the PM,suggesting that the linear form of the extended stochastic state observer driven by the bounded stochastic dynamics is sufficient to construct the overall explicit model of the disturbance of the PM.Consequently,it brings great convenience for controller design,only bandwidth-parameterization in the frequency domain needs to be tuned.The simulation results prove and clarify the design and the criticalities,indicating that the disturbance rejection control of the PM compatible with the resolution of the gravity field can be explicitly achieved in a timely manner while the observer bandwidth is fixed as the cutoff frequency of the mid-frequency band. The proposed NCS architecture gives accurate results without complicated tuning in actual implementation,which is beneficial to a wide range of the futuristic space science missions,such as the ultra-precision remote sensing,detection of gravitational waves and the astronomical observation. Acknowledgment The authors would like to show gratitude to Shanghai Institute of Satellite Engineering for valuable discussion and sharing experimental data during the course of this research.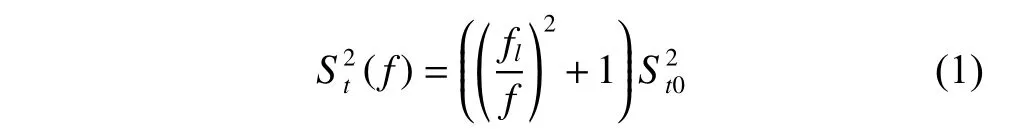
2.2 Frame definition and control system configuration

2.3 Hierarchical control architecture

3.Controller design
3.1 Extended stochastic state observer based control for PM
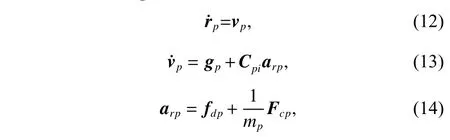
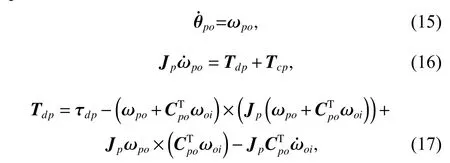
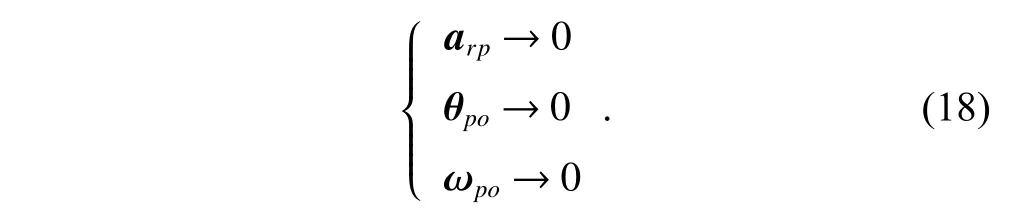
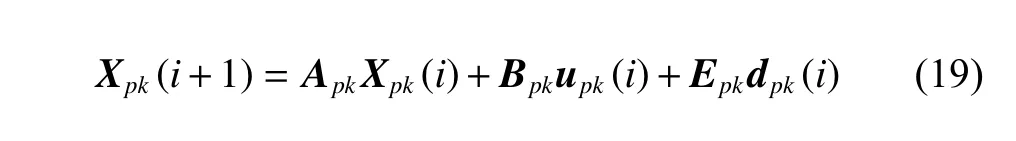
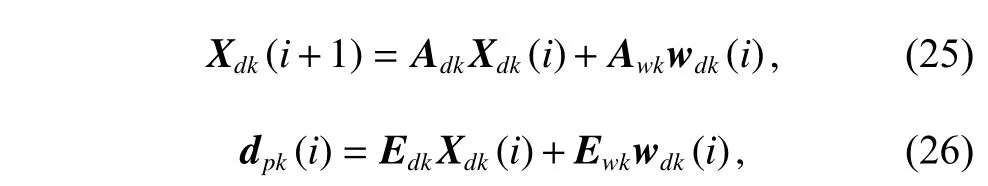



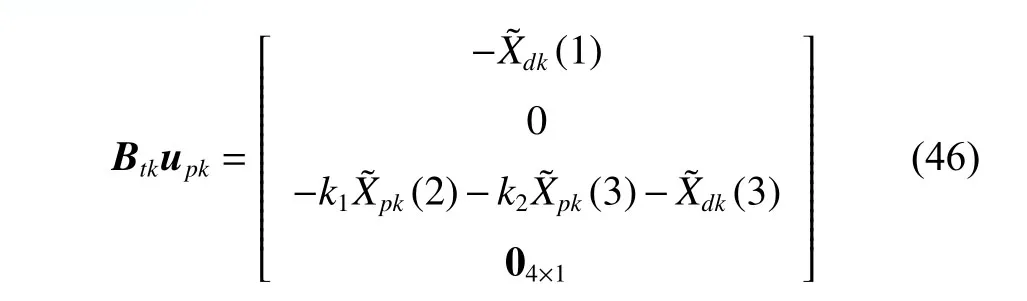
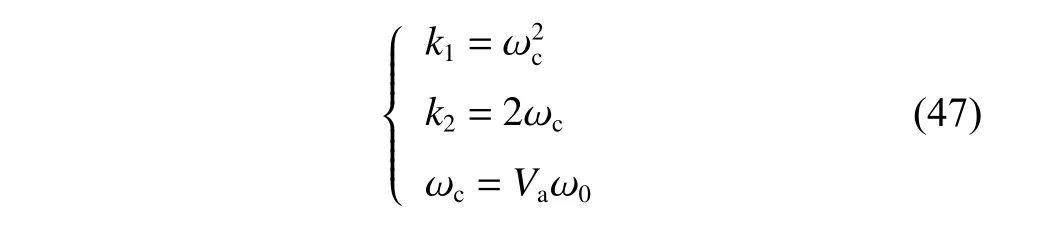
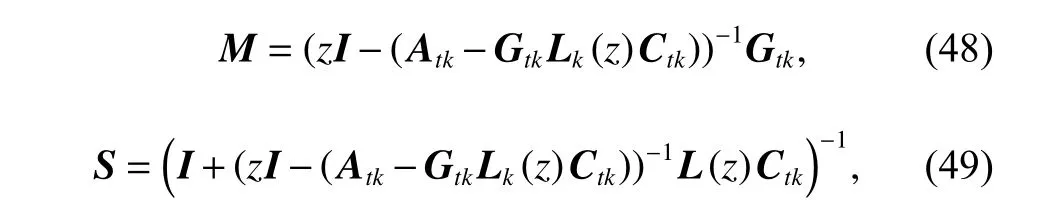
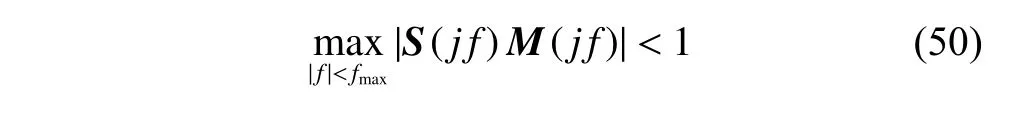
3.2 Collaborative control for SM
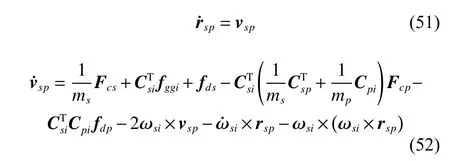
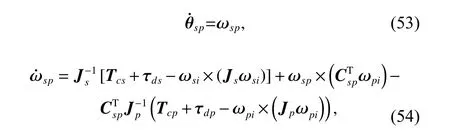

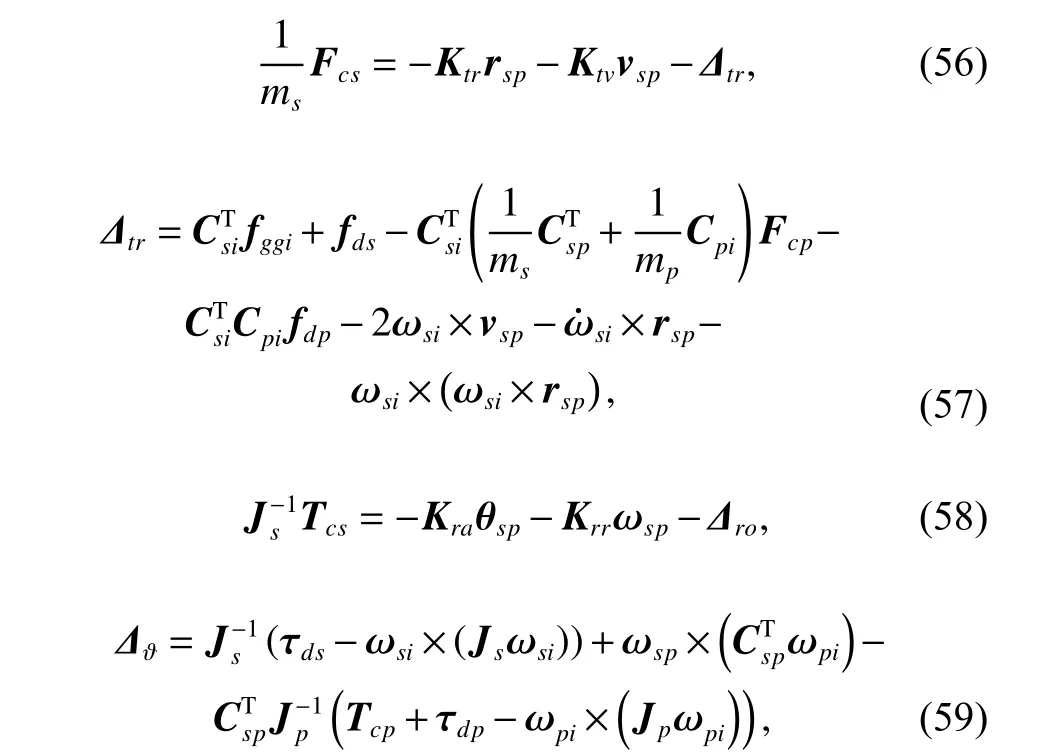
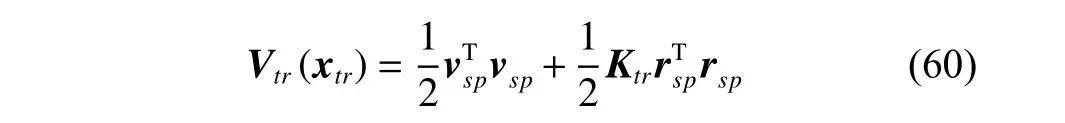
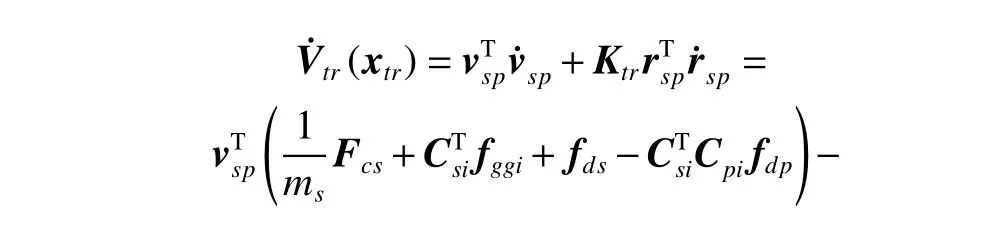

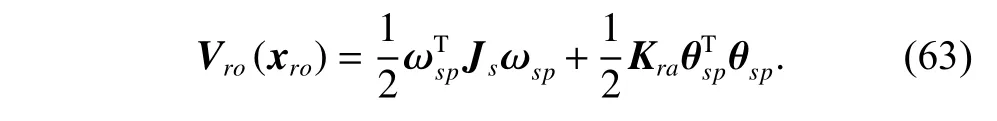
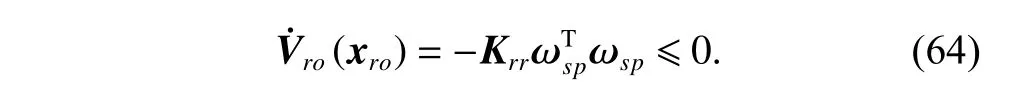
4.Numerical simulation
4.1 Initial conditions


4.2 Bandwidth-parameterization
4.3 Disturbance-observer simulation
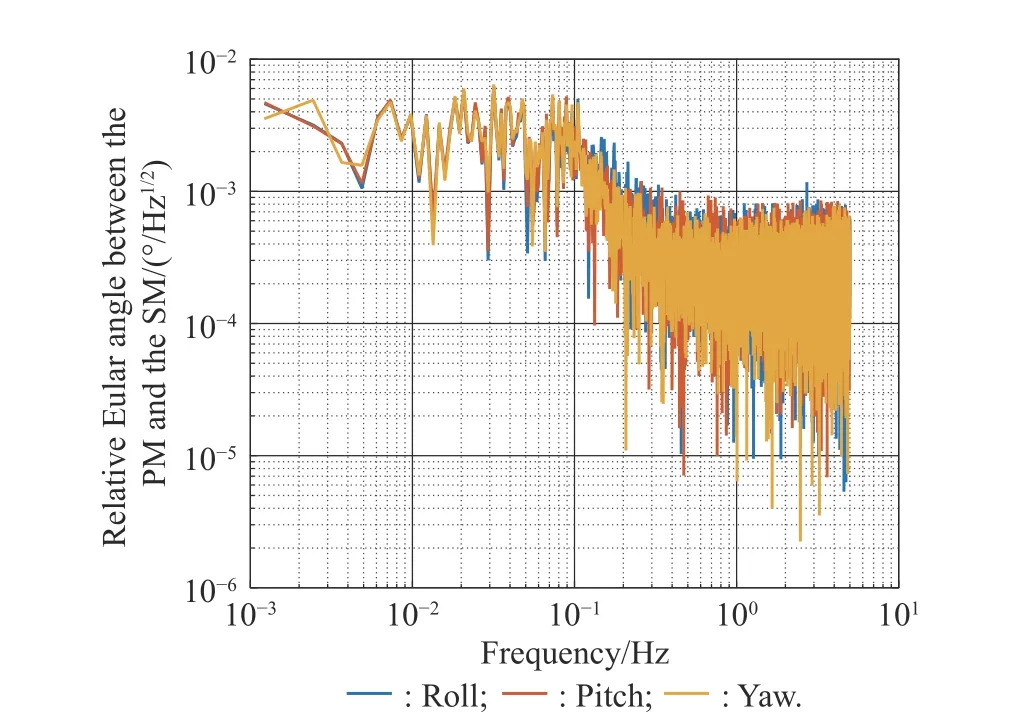
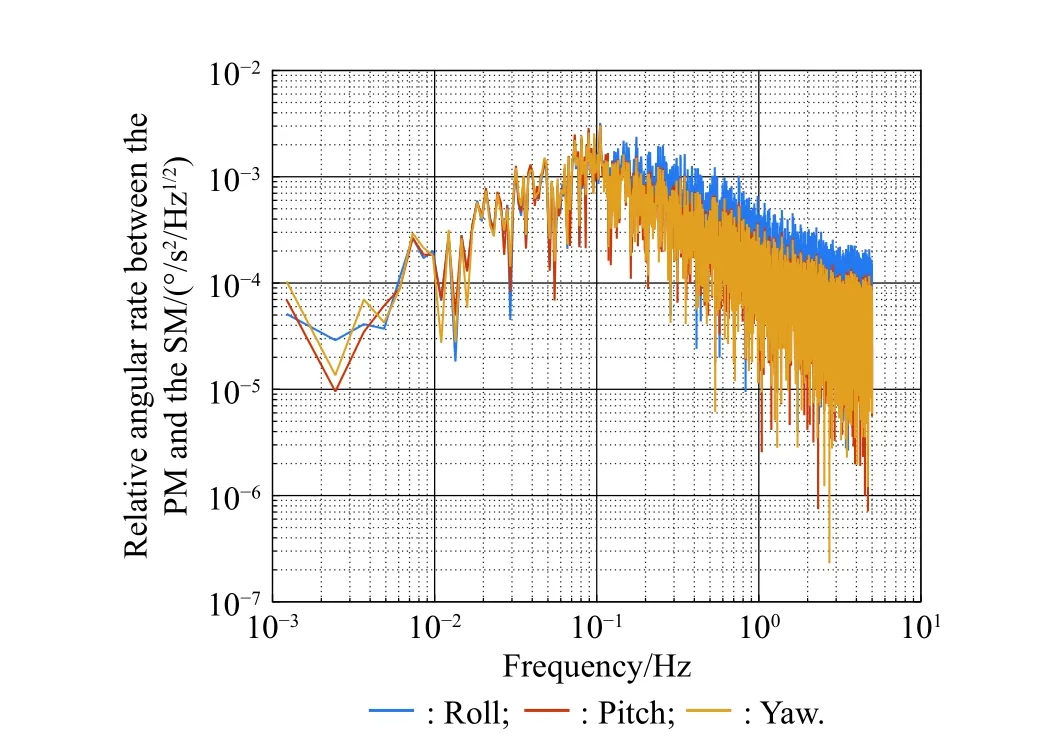
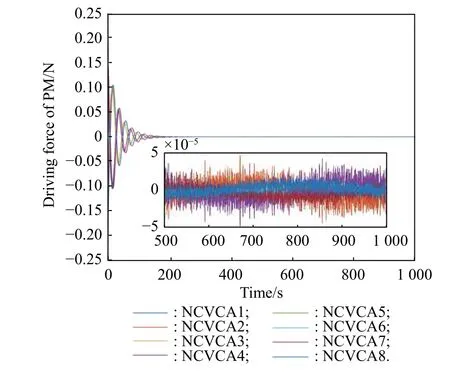
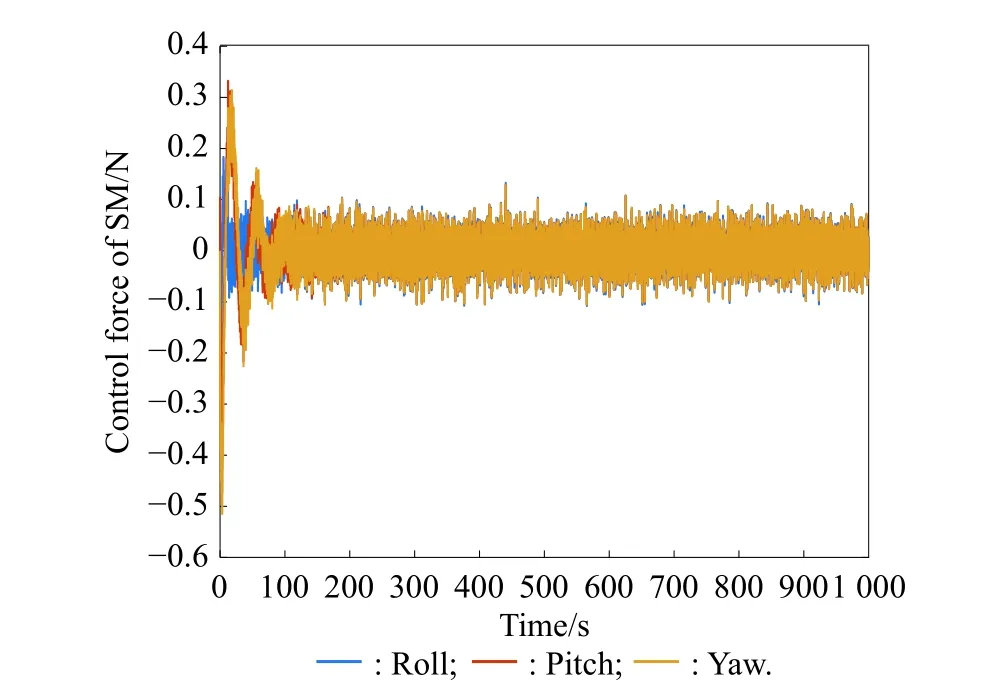
4.4 Control results and discussion
5.Conclusions
 Journal of Systems Engineering and Electronics2021年2期
Journal of Systems Engineering and Electronics2021年2期
- Journal of Systems Engineering and Electronics的其它文章
- Data-driven evolutionary sampling optimization for expensive problems
- A dual population multi-operator genetic algorithm for flight deck operations scheduling problem
- Observation scheduling problem for AEOS with a comprehensive task clustering
- An improved estimation of distribution algorithm for multi-compartment electric vehicle routing problem
- VCR-LFM-BPSK signal design for countering advanced interception technologies
- RFC:a feature selection algorithm for software defect prediction
