Three-dimensional impact angle constrained distributed cooperative guidance law for anti-ship missiles

LI Wei ,WEN Qiuqiu,* ,HE Lei ,and XIA Qunli

1.School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China;2.Sichuan Institute of Aerospace Systems Engineering,Chengdu 610100,China

Abstract: This paper investigates the problem of distributed cooperative guidance law design for multiple anti-ship missiles in the three-dimensional (3-D) space hitting simultaneously the same target with considering the desired terminal impact angle constraint.To address this issue,the problem formulation including 3-D nonlinear mathematical model description,and communication topology are built firstly.Then the consensus variable is constructed using the available information and can reach consensus under the proposed acceleration command along the line-of-sight (LOS) which satisfies the impact time constraint.However,the normal accelerations are designed to guarantee the convergence of the LOS angular rate.Furthermore,consider the terminal impact angle constraints,a nonsingular terminal sliding mode (NTSM) control is introduced,and a finite time convergent control law of normal acceleration is proposed.The convergence of the proposed guidance law is proved by using the second Lyapunov stability method,and numerical simulations are also conducted to verify its effectiveness.The results indicate that the proposed cooperative guidance law can regulate the impact time error and impact angle error in finite time if the connecting time of the communication topology is longer than the required convergent time.

Keywords:distributed cooperative guidance law,impact angle constraint,communication topology,nonsingular terminal sliding mode (NTSM) control,finite time convergent.

1.Introduction

With the urgent demand of modern warfare,most advanced guidance laws aim to drive the missile to intercept a specific target with zero miss distance and raise the damage effectiveness.The proportional navigation guidance(PNG) law has been proven to be a mature guidance algorithm for attacking the stationary or weak-maneuverable target,and got widely applied [1].The key principle of PNG is to force the line-of-sight (LOS) angular rate to converge to zero,and then achieve zero miss distance engagement if neglecting the measurement noise and external perturbation [2].However,with the development of modern defense and antimissile technology,some ships have been equipped with lots of self-defense measures,such as surface-to-air missile systems,electronic interference and so on,thus single missile combat is easy to be intercepted and cannot effectively suppress and destroy the enemy field [3,4].Therefore,saturation attack has fully highlighted its strategic advantages,which can increase the ability of missiles to attack and penetrate important targets,and has attracted much attention of various countries.Saturation attack requires that the firepower be accurately allocated to the designated target,and that the target be hit at a specified time with a specified number of missiles.The saturation attack tactic is developed on the basis of the salvo tactic,namely through launching a large number of missiles and penetrating from multi-direction,and then at least one missile can penetrate the enemy firepower and destroy the target.The salvo attack puts forward higher requirements for the missile guidance law,which controls each missile to satisfy the desired impact time constraint individually,or builds a communication network among all missiles to ensure the coordination of arrival time.

In the current literature,a linearized optimal impact time control guidance (ITCG) obtained by a simple combination of classical PNG term and impact time error feedback term,was proposed in [4],which seems to be the first paradigm in the area of salvo attack of multiple missiles.After that,the approach of [4]was improved by using a time-varying navigation gain in [5]and generalized PNG based on nonlinear formulation in [6].Besides,the sliding-mode control [7],Lyapunov-based control [8],feedback linearization [9],virtual leader approach [10],and some other advanced guidance strategies [11−14]have been successfully employed for satisfying the impact time constraint.

For anti-ship missiles,the impact angle constraint is required not only to increase lethality of warheads but also to escape the limited defense zone of the target.One of the earliest impact angle guidance laws was proposed in[15],where the impact angle constraint was satisfied by posing a linear quadratic control problem with time-varying gains.Up to now,more and more studies have focused on the impact angle control,from the biased proportional navigation guidance (BPNG) law [16]to the optimal control guidance law [17,18]with the impact angle constraint,from the Lyapunov method [19]to the backstepping method [20],and even converting the impact angle control problem into a second-order cone programming problem [21].By considering both impact time and angle constraints simultaneously,Lee et al.[22]expanded the approach from [4]to analysis,and then proposed a guidance law to control the impact time and impact angle.Zhang et al.[23]derived a new biased PNG law to meet the terminal impact time and impact angle requirements.Hu et al.[24]proposed a two stages guidance strategy,which in the first stage adopts the NTSM guidance law to intercept the virtual target with a specified impact angle in finite time,and in the second stage employs the PNG to keep the missile traveling with an invariant flight-path angle.

Note that most previous impact time guidance laws are dedicated to the two-dimensional (2-D) plane,however,in practice,the anti-ship missiles fly in the three-dimensional (3-D) space.Thus,the cross-couplings effect between the horizontal and the vertical channels cannot be ignored,and the impact angle constraint also needs to be considered.Therefore,designing a 3-D cooperative guidance law with impact time and impact angle constraints for anti-ship missiles is very significant.Based on the aforementioned purposes,this paper aims to propose a novel distributed cooperative guidance law to make multiple missiles in the 3-D space attack the same target simultaneously at the desired impact angles.The normal accelerations are designed to make the LOS angle converge to the desired LOS.Meanwhile,the tangential acceleration is designed to make the consensus variable defined by using available information reach consensus based on the graph theory,and hence to achieve the simultaneous attack.

The structure of this paper is organized as follows.In Section 2,the background and preliminaries are given,which include 3-D mathematical model building and communication topology theory.Next the design details of the proposed guidance law are presented in Section 3.Finally,numerical simulations are conducted in Section 4 and related conclusions are offered in Section 5,respectively.

2.Problem formulation and preliminaries

The scenario of multiple missiles attacking the same target in the 3-D space is shown in Fig.1,where Mi(i=1,2,···) and T denote the anti-ship missiles and the target,respectively.The missiles can exchange the information according to the communication topology.Therefore in this section,the mathematical model of 3-D missile kinematics at the terminal engagement phase is built,and some assumptions and lemmas are also shown for problem formulation and later guidance law design.

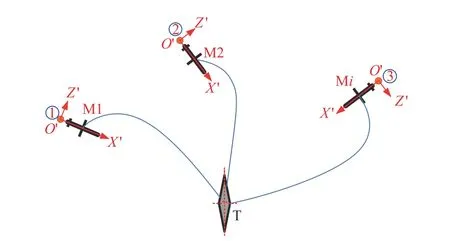
Fig.1 Scenario of multiple missiles attacking the target

2.1 Problem statement

To perform the complete missile-target engagement,the nonlinear dynamics of 3-D situation is introduced based on the following basic assumptions [25,26].

(i) The missile and the target are considered as the ideal point-mass models in the 3-D space.

(ii) The angle-of-attack of the missile is small enough to be neglected.

(iii) The seeker and autopilot dynamics of the missile are fast enough in comparison with the guidance loop.

(iv) The target moves slowly or remains stationary.

Under above assumptions,the 3-D engagement geometry of a missile attacking the target is shown in Fig.2,whereO−xI yI zIdenotes the inertial reference coordinate frame fixed on the ground,andOL−xL yL zLdenotes the LOS coordinate system.rrepresents the relative distance between the missile and the target,and λpand λydenote the elevation and the azimuth angles of the LOS to the inertial coordinate system,respectively. θ and ψ denote two Euler angles from the LOS coordinate system to the missile velocity coordinate system. σ is the velocity leading angle.

DefineV=[Vr,Vp,Vy]Tas the relative velocity vector between the missile and the target in the LOS coordinate system,and then according to Fig.2,it can be obtained as

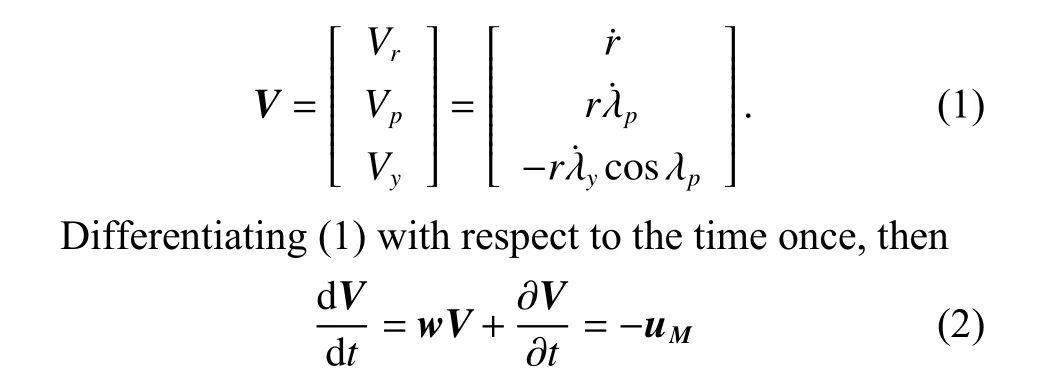
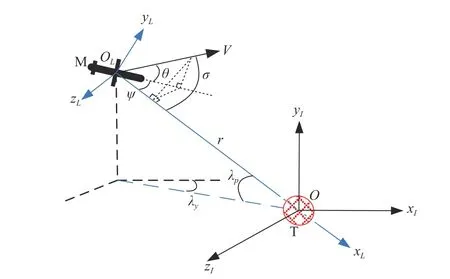
Fig.2 3-D engagement geometry

where dV/dtand ∂V/∂tdenote the derivatives of the relative velocity vector to time in the inertial coordinate systemO−xI yI zIand the LOS coordinate systemOL−xL yL zL,respectively.uMstands for the missile acceleration vector in the LOS frame,and is defined as[ur,up,uy]T.wdenotes the rotation angular velocity vector of the LOS frame relative to the inertial frame,which can be expressed as

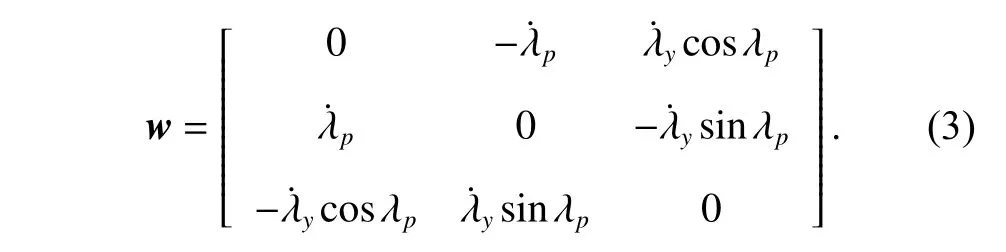
Substituting (1) and (3) into (2),the nonlinear engagement dynamics between the missile and the target in the LOS frame can be written [27]as

Define the consensus variabletgorepresents the remaining flight time between the missile and the target,which is called as time-to-go.In the real interception process,the relative velocity component along the LOS between the missile and the target changes little,so the time-to-gotgo,iof theith missile can be approximately expressed as

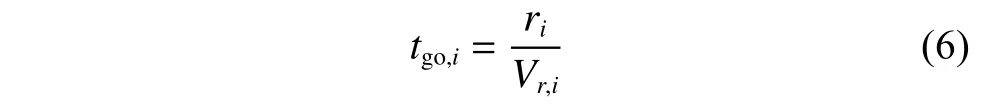
whereriandVr,idenote the relative range and velocity component along the LOS of theith missile,respectively.

Differentiating (6) with respect to time yields

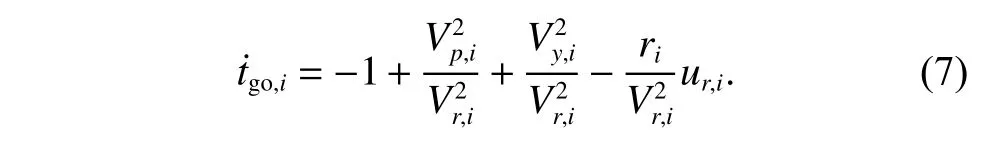
In order to design a cooperative guidance for multiple missiles with considering the impact time constraint,we introduce the variabletimp,idenoting the predicted impact time for theith missile,which is defined as

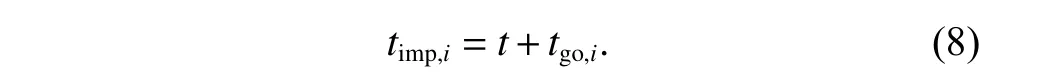
Differentiating (8) and substituting (7) into it results in

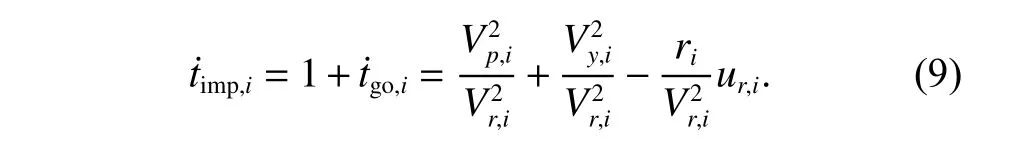
Based on the above-mentioned process,it is obvious that the objective of this paper is to design the control law forupanduyto make the LOS rateof each missile converge to zero in finite time,and then use the acceleration commandurto force all missiles to intercept the target simultaneously.Furthermore,without loss of generality,consider the terminal impact angle constraints for each anti-ship missile during the design procedure.

2.2 Preliminary of communication topology and some lemmas

The cooperative attack problem for multiple missiles is just like the multi-agent system consensus problem,which needs the information exchange between the neighbor flight vehicles through onboard sensors.Here,we use the undirected graphG=(υ,ε,A) to describe the communication topology,where υ={vi:i=1,2,···,N} is the set of vertices that representnmissiles,ε ⊆υ×υ is the set of edges that stand for the relationship between two neighboring missiles,andA=[ai j]∈Rn×nis called the weighted adjacency matrix with nonnegative adjacency elementsaij.If theith missile and thejth missile are adjacent,representing they can communicate with each other,thenMoreover,there existsaii=0 for alli=1,2,···,nandaij=ajibecause the graphGis undirected.

Lemma 1[28]Define the matrixas the Laplacian matrix of the graph,which is given as

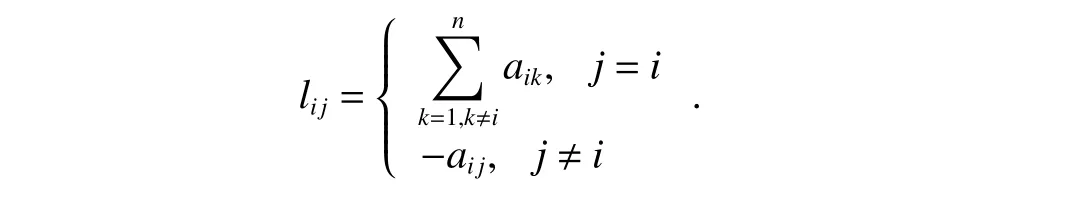
Lhas the following properties:

(i) 0 is an eigenvalue ofLand 1=[1,1,···,1]T∈Rnis the associated eigenvector.

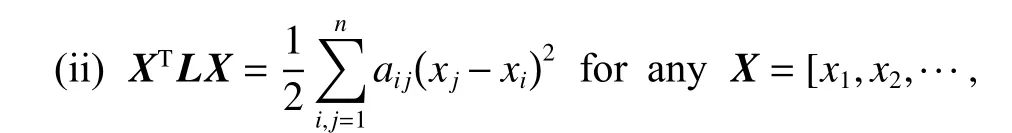
In summary,the objective of this paper is designing the guidance law to guide all missiles to reach the target simultaneously with the desired terminal impact angle based on the above background.

3.Cooperative guidance law design

3.1 ITCG law design

In this section,we will firstly propose a novel ITCG law in the 3-D space and analyze its properties.

Therefore,in terms of (10),it can be observed that the impact time for each missile mainly depends on the tangential inputur,i,which can be designed to achieve the consensus of time-to-go according to the following procedure.

3.1.1 Tangential design

Theorem 1Assumingis the desired interception time,and when the communication topology is connected between multiple missiles,the consensus algorithm forur,ican be designed as

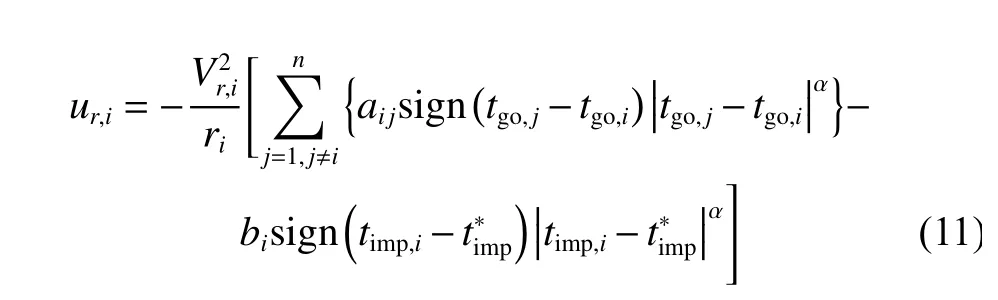
wherebi0 and α>0 are guidance gains,which are designed to obtain the satisfactory convergence rate.bi>0 denotes theith missile can obtain the information of the designed impact timeotherwisebi=0.The above guidance law can guarantee the consensus of impact time for all missiles during the terminal guidance phase,and next is the proof of its convergence.

ProofDefine that the variablerepresents the impact time error of theith missile,and then consider the following Lyapunov function candidate:

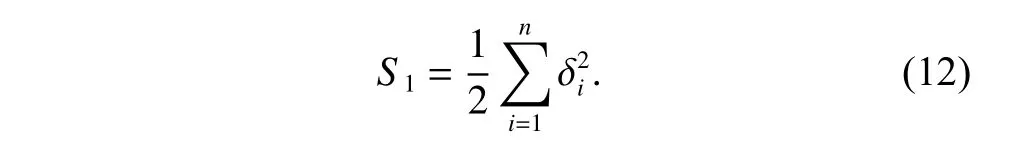
The time derivative of this Lyapunov candidate along the trajectory of system (11) can be expressed as

3.1.2 Normal design

3.2 Impact time and angle control guidance law

In this section,we consider both the impact time constraint and the terminal impact angle constraint perpendicular to the LOS.Under this condition,a novel NTSM surface is built and a finite time convergent control law of normal accelerationsupanduyis proposed to drive the LOS angular rate and LOS angle tracking error to converge to a small neighborhood around zero in finite time during the whole engagement phase.

4.Numerical simulations

In this section,the effectiveness of the proposed cooperative guidance law is demonstrated through numerical simulations,in which three missiles are considered to intercept a stationary target with different initial conditions.The target is assumed to be at the position of (0,0,0) m while the initial conditions for the three missiles are shown in Table 1.Additionally,in the simulations,three different communication topologies are considered in Fig.3,where the first two ones are connected while the last one is unconnected.

Table 1 Initial flight parameters of multiple missiles

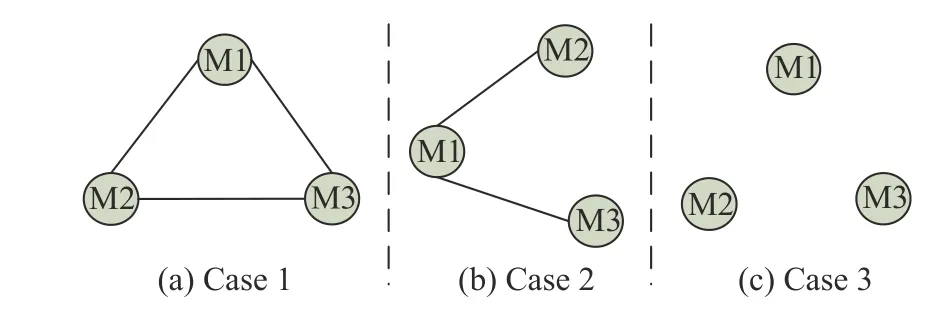
Fig.3 Communication topology among three missiles

4.1 Simulation results of impact time control

Considering the engagement scenario topology Fig.3(c)firstly,and then the corresponding adjacency matrixA3can be described as

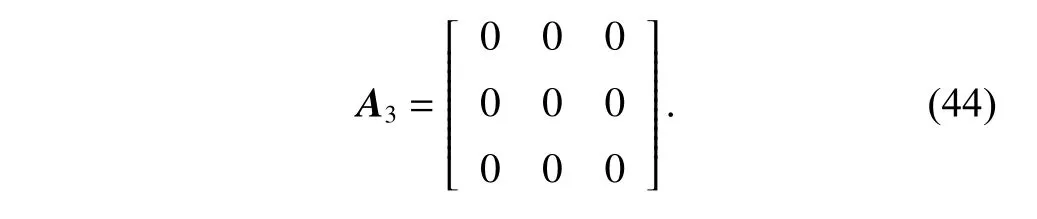
It is assumed that only the 1st missile (M1) can obtain the desired impact time information,then (11) can be simplified as (45) in this condition.

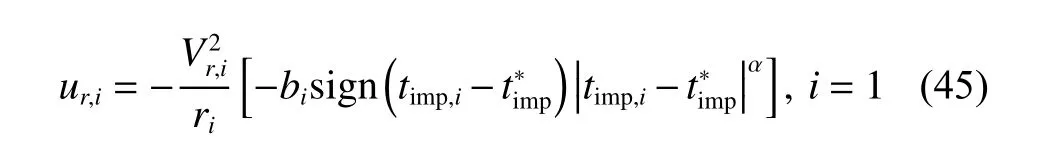
The control law parameters are chosen as α=0.5,bi=1 for (45),andNi=4,βi=1.0 and ηi=0.5 for (21).After that,to verify the effectiveness of the proposed guidance algorithm,let the desired impact time65 s,70 s and 75 s,respectively.The simulation step is set to be 5 ms,and the simulation results for M1 in this case are shown in Fig.4.

Fig.4(a) shows the history of the time-to-go for M1 with these three cases of desired impact timewhich reveals that the proposed guidance law satisfies the impact time constraint precisely.The impact time error of the proposed guidance law turns out to be less than 0.01 s in our simulations.Fig.4(b) indicates that the zero miss distance can be achieved as the flight time approaches to the desired impact time.Furthermore,the missile acceleration command along the LOS produced by the proposed guidance law with differentis provided in Fig.4(c).Clearly,a longer convergence phase is required to regulate the impact time error with a larger desired impact time under the same initial conditions.

To further investigate the performance of the proposed impact time guidance law,we next consider the first engagement scenario Fig.3(a),and the corresponding adjacency matrixA1can be obtained as

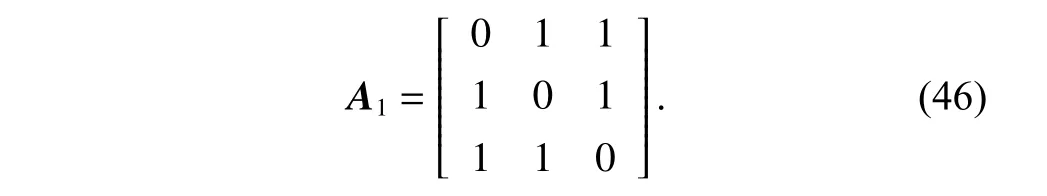
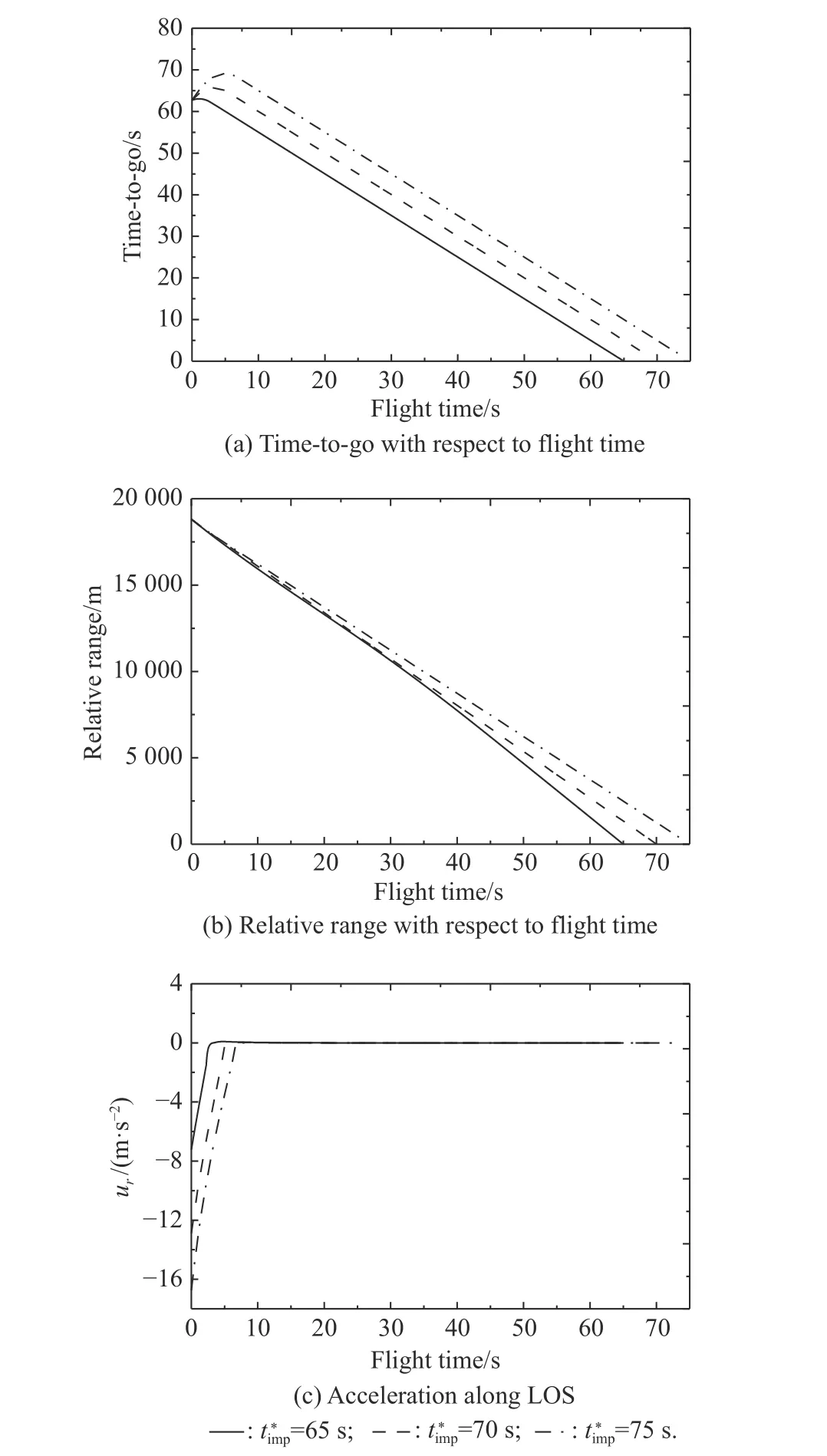
Fig.4 Simulation results for M1 with respect to different desired impact time

Keep the control law parameters for (11) and (21) consistent with the previousdesign.In addition,the desired interception time for all missiles is chosen asin this case.The simulation is terminated when the maximum range-to-go is less than 0.5 m,and the corresponding simulation results are shown in Fig.5.

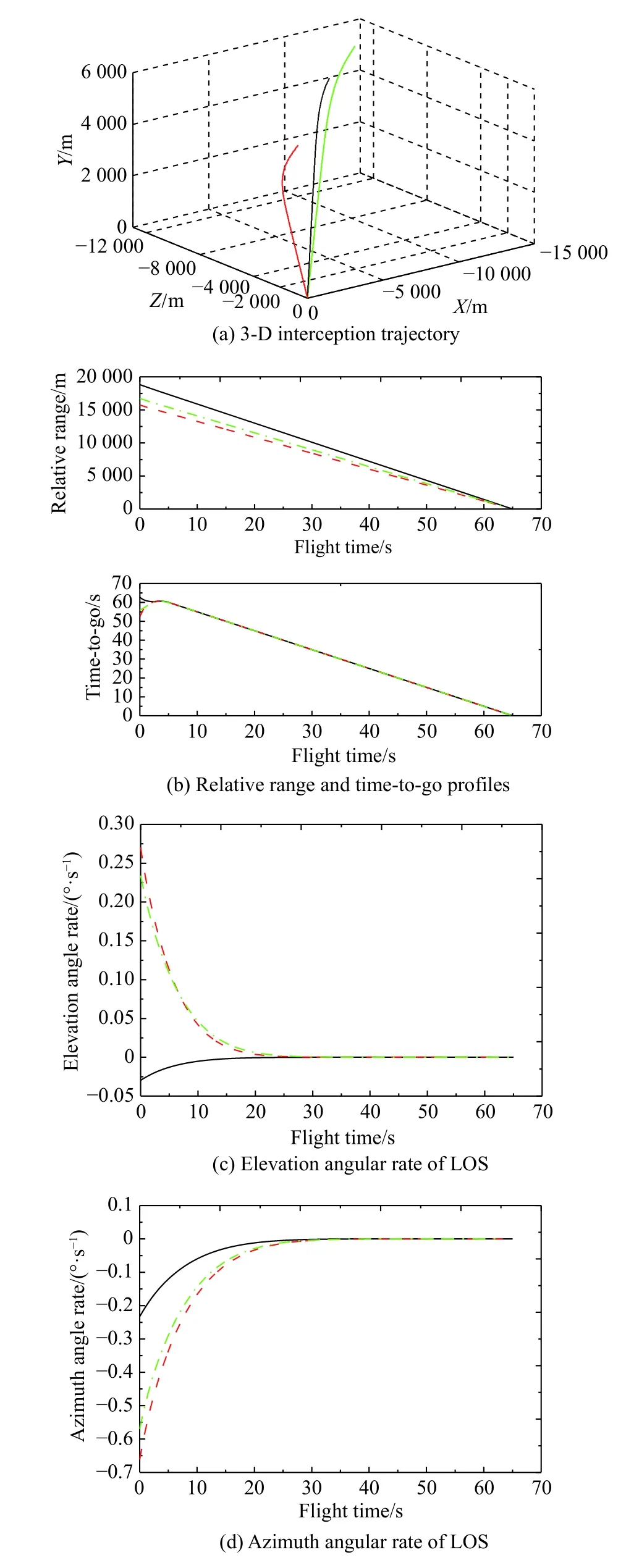
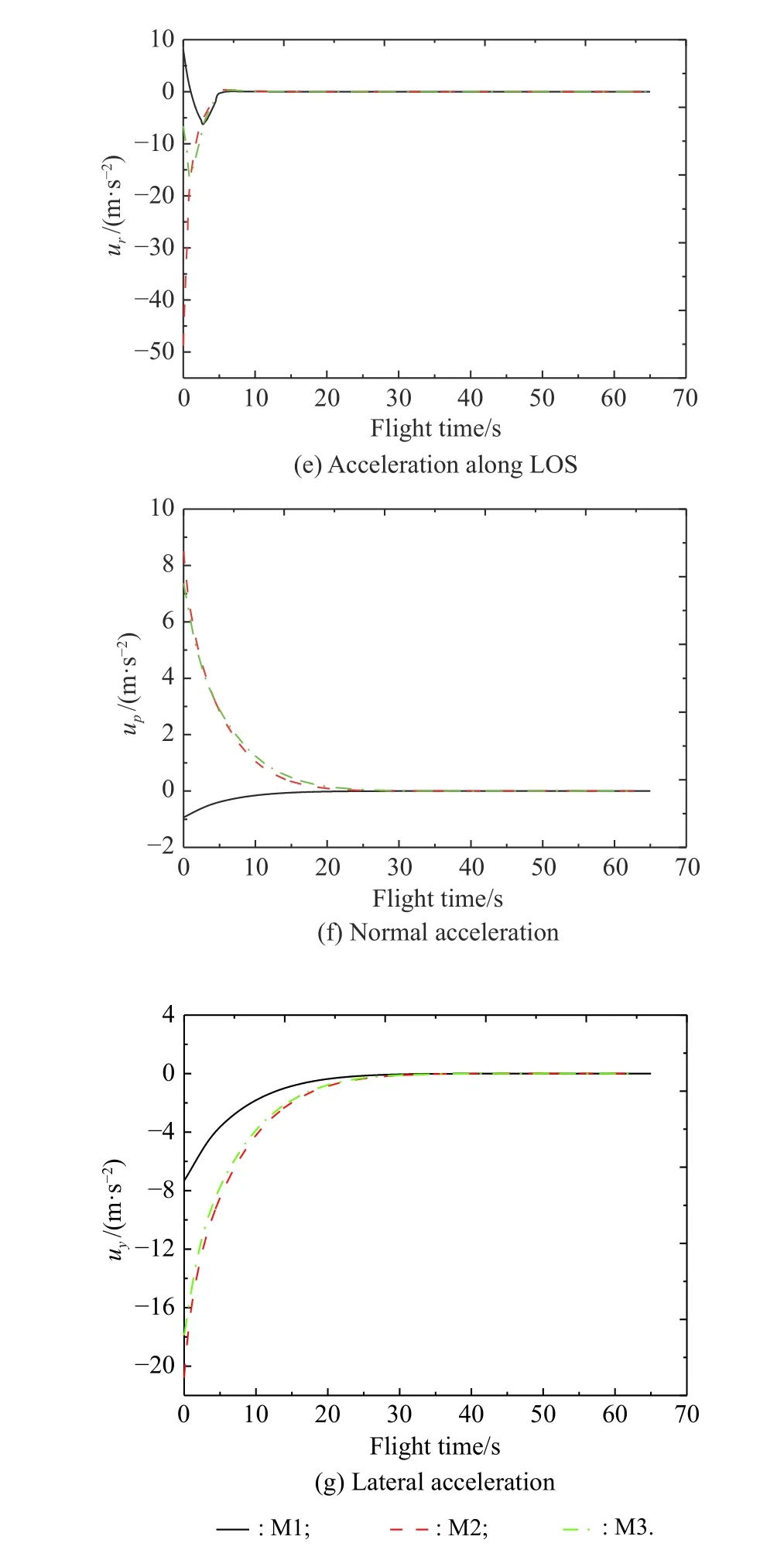
Fig.5 Simulation results with the desired impact time

Fig.5(a) compares the 3-D interception trajectory for these three different initial conditions,which shows that the cooperative attack mission is accomplished.Then,the relative range and time-to-go profiles with respect to flight time are shown in Fig.5(b).In Fig.5(b),it can be seen that the time-to-go of these three missiles reaches at an agreement at about 3.7 s,and the simultaneous attack is achieved with the desired impact time 65 s.The result conforms with the proof of Theorem 1,since we can easily verify that the convergence time under this case is shorter than the required converge timeBesides,it can be noted from Fig.5(c) and Fig.5(d) that the elevation angular rate and the azimuth angular rate of LOS converge to zero in finite time.The missile acceleration commands produced by the proposed guidance law with respect to flight time is produced in Fig.5(e) to Fig.5(g),which can be found that the convergence rate of the acceleration along LOS is faster than that of the normal acceleration and lateral acceleration.

4.2 Simulation results of impact time and angle control

In this situation,choose the control law parameters α=0.5,bi=1 for (11),andp=2,q=3,k1=0.5,k2=0.1,v1=10,v2=10,τ1=τ2=2.1 for (33).The designated impact time is set as=65 s,and the desired impact angle for these three missiles are taken as λimpf=−40◦,−60◦,−80◦and λimy f=−20◦,−40◦,−60◦in the elevation and azimuth directions,respectively.The simulation results are shown as Fig.6,which implies that the proposed guidance law can satisfy the requirements for the designated impact time and impact angle.

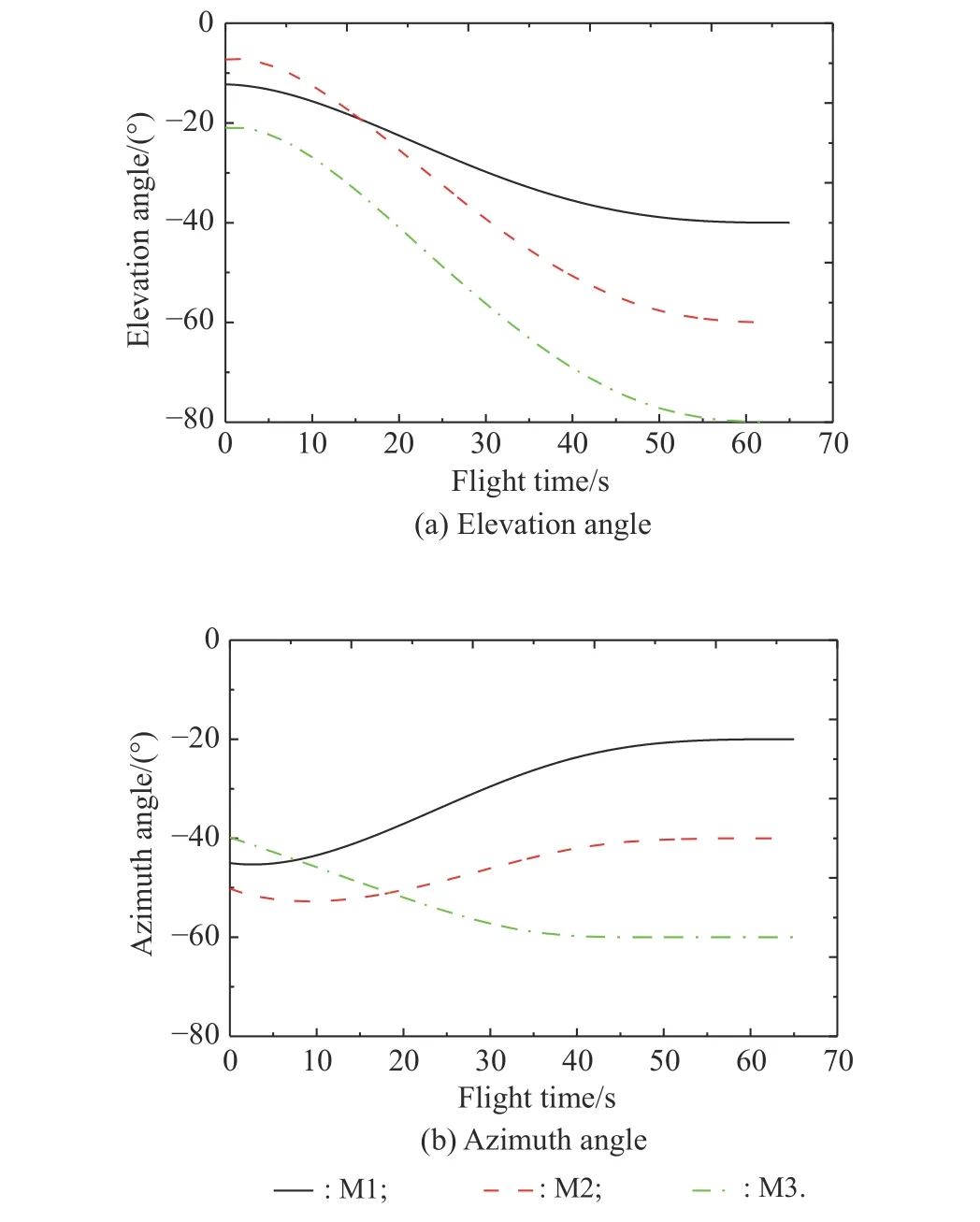
Fig.6 Simulation results with different impact angle constraints

However,to increase the damage performance,the large impact angle constraint usually needs to be considered in the actual combat process.Therefore,the desired impact angle for these three missiles are all taken as λimpf=−80◦and λimyf=−60◦,respectively,and the corresponding simulation results are presented in Fig.7.It can be observed that the LOS angle for all missiles tend to the designated impact angle along with the time-to-go error going to zero.Both the impact time control and impact angle control are achieved finally,as we expected.

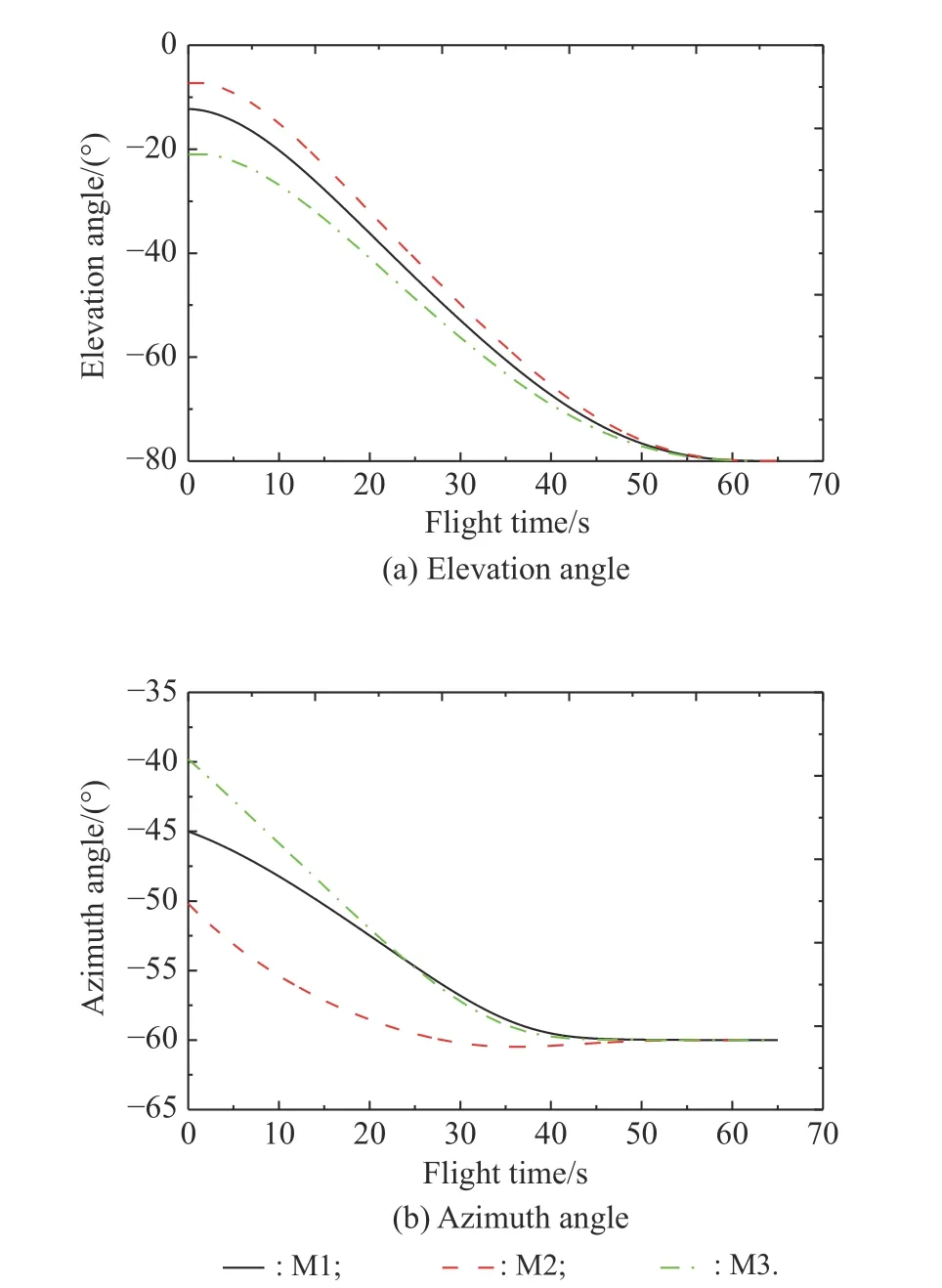
Fig.7 Simulation results with the same impact angle constraint

The rest simulation results,including the interception trajectories,relative range and time-to-go profiles,LOS angular rates,and acceleration commands,are presented in Fig.8 with respect to the desired impact angle λimpf=−80◦and λimyf=−60◦.From Fig.8(a),it can be known that the trajectories become more curved than that without impact angle controlling.The time-to-go index of these three missiles reaches an agreement quickly,as shown in Fig.8(b).In addition,Fig.8(c) to Fig.8(g)show that the LOS angular rates and acceleration commands both converge to a small neighborhood around zero in a certain time,which illustrates that the proposed 3-D guidance law can regulate the impact time error and impact angle error,in accordance with the expectant design.

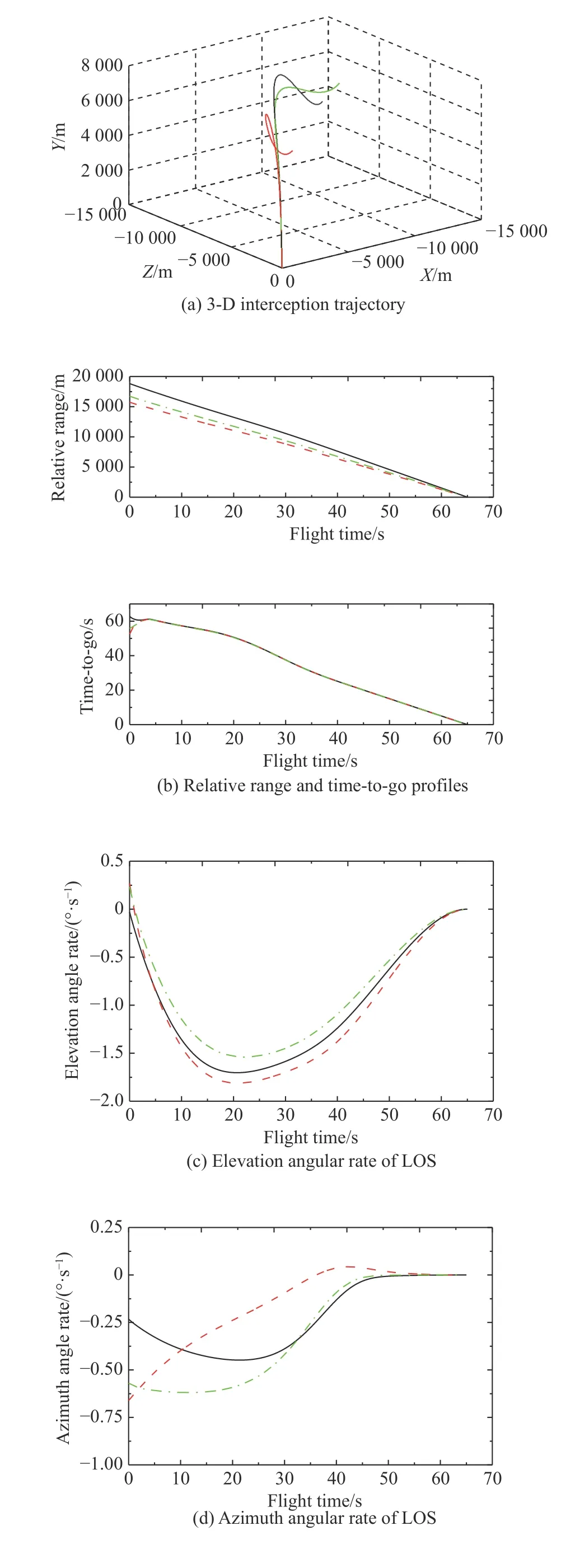
Fig.8 Simulation results with the designated impact time and impact angle

4.3 Simulation results of switching topology

In this section,we mainly focus on the situation with the switching topology induced by the communication fault during the flight.As shown in Fig.3,the communication topology switches to topology Fig.3(c) duringand then switches to topology Fig.3(b),which means the graphGmaintains disconnecting for 7 s.The simulation results for this case are shown in Fig.9.

It can be seen from Fig.9(a) that the time-to-go of these three missiles reaches an agreement at about 13.54 s.From Fig.9(b),the acceleration along LOS of all missiles has a jump when the graph is reconnected,and gradually converges to near zero with respect to flight time.In summary,we can discover that this communication topology may not affect the finite-time consensus,but may deteriorate the consensus time.

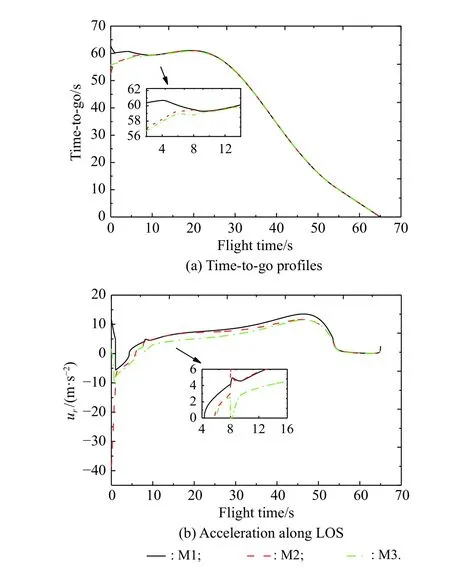
Fig.9 Simulation results under switching topology

5.Conclusions

In this paper,the cooperative guidance problem for multiple anti-missiles in the 3-D scenarios to achieve a salvo attack is discussed with the desired terminal impact angle constraint perpendicular to the LOS.The proposed cooperative guidance scheme is divided into two different parts:the tangential acceleration command is designed to make the time-to-go variable reach an agreement in finite time based on the available flight information and communication topology theory.The normal accelerations are designed to force the LOS rate to converge to a small neighborhood around zero,and ensure the terminal impact angle constraint is satisfied with the help of the nonsingular terminal sliding mode control strategy.Numerical simulations strongly demonstrate the effectiveness of the proposed formulation,the simultaneous attack is achieved with impact time error and LOS rate both equal to zero.Furthermore,the killing efficiency of missiles can also be significantly improved by satisfying the terminal impact angle constraint by using the proposed guidance law.Finally,numerical simulation results verify the effectiveness of the proposed method.