Multi-objective reconfigurable production line scheduling for smart home appliances
LI Shiyun,ZHONG Sheng,PEI Zhi,YI Wenchao,CHEN Yong,WANG Cheng,and ZHANG Wenzhu
College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou 310023,China
Abstract:In a typical discrete manufacturing process,a new type of reconfigurable production line is introduced,which aims to help small-and mid-size enterprises to improve machine utilization and reduce production cost.In order to effectively handle the production scheduling problem for the manufacturing system,an improved multi-objective particle swarm optimization algorithm based on Brownian motion (MOPSO-BM) is proposed.Since the existing MOPSO algorithms are easily stuck in the local optimum,the global search ability of the proposed method is enhanced based on the random motion mechanism of the BM.To further strengthen the global search capacity,a strategy of fitting the inertia weight with the piecewise Gaussian cumulative distribution function (GCDF) is included,which helps to maintain an excellent convergence rate of the algorithm.Based on the commonly used indicators generational distance (GD) and hypervolume (HV),we compare the MOPSO-BM with several other latest algorithms on the benchmark functions,and it shows a better overall performance.Furthermore,for a real reconfigurable production line of smart home appliances,three algorithms,namely non-dominated sorting genetic algorithm-II (NSGA-II),decomposition-based MOPSO (dMOPSO) and MOPSO-BM,are applied to tackle the scheduling problem.It is demonstrated that MOPSO-BM outperforms the others in terms of convergence rate and quality of solutions.
Keywords:reconfigurable production line,improved particle swarm optimization (PSO),multi-objective optimization,flexible flowshop scheduling,smart home appliances.
1.Introduction
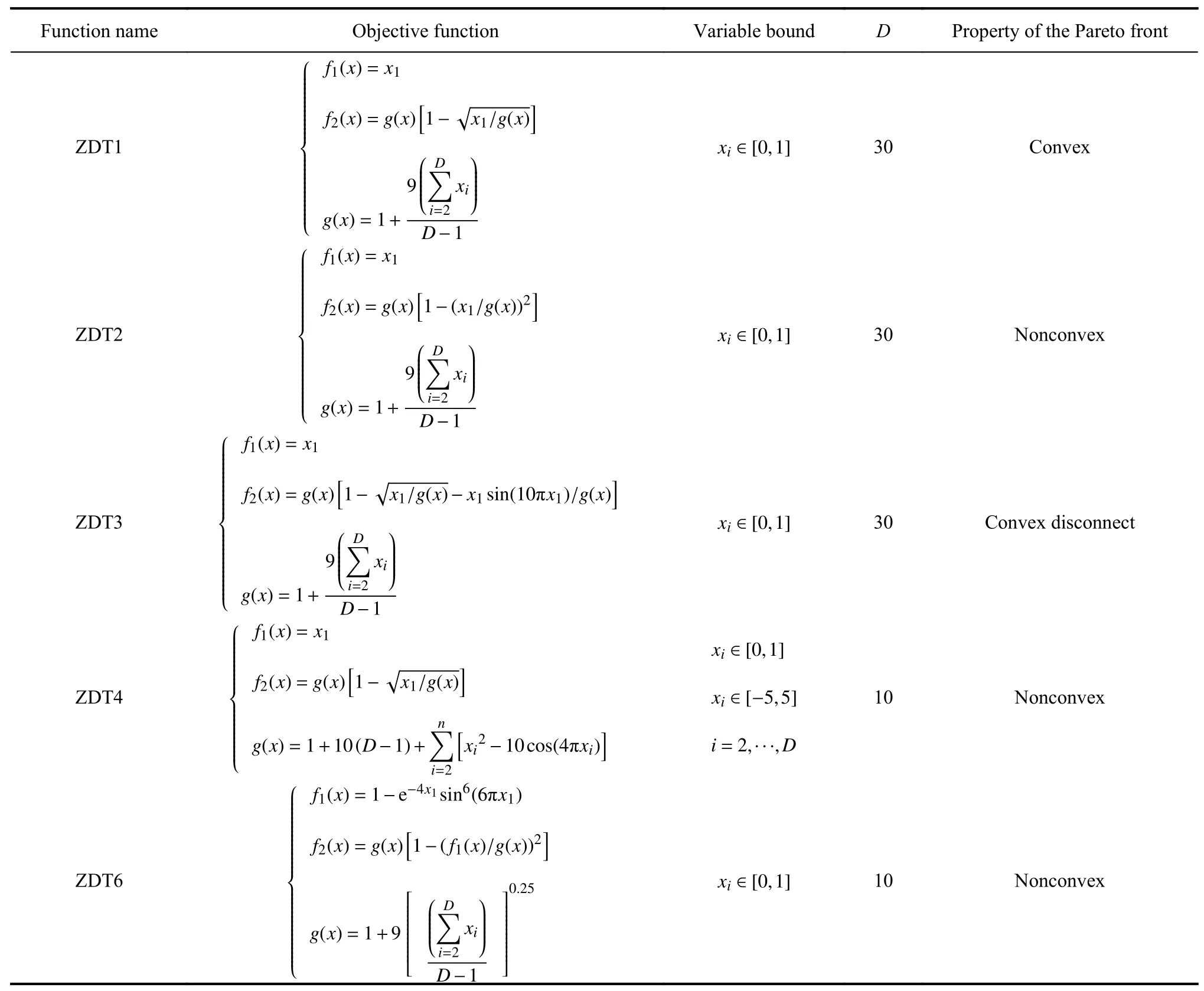
With the rapid development of information technology,the global manufacturing market has entered a digitalized age,and fierce competition of the manufacturing technology and managerial strategy increasingly affect the survival and development of the enterprises.In order to meet the growing market demand,the production paradigms of most companies have shifted from the original mass production to the flexible production with smaller batches [1].However,for small-and mid-size enterprises(SMEs),to cope with the ever-changing customer requirements is challenging,given that the manufacturing is resource and equipment sensitive.In response to this challenge,the development of a reconfigurable production line could be a fast deployable solution.In the past several decades,many researchers have studied the reconfigurable production line scheduling problem,which are summarized in Table 1.By consulting the related literature,it is found that most of the existing papers study the production scheduling from a mathematical perspective,without considering the configurations of the production line [2−21].A highly flexible production setting may bring greater benefits to the manufacturing system.
To echo that purpose,this paper proposes a new mode of reconfigurable manufacturing system,where the modules with different functions are assembled together to form a dedicated production line.The reconfigurable production line could be decomposed into separate production units,which preserves great flexibility and saves cost significantly in comparison with the traditional one-time installation of equipment.
Besides the production line itself,this reconfigurable setting poses great challenges on the scheduling algorithm.A good schedule could greatly reduce processing costs,shorten the processing completion cycle,improve the utilization rate of equipment,and directly increase the economic benefits of the enterprise.Currently,the scheduling strategy for such a reconfigurable production line mainly relies on the experiences of the planners,which leads to many problems such as low production efficiency,high equipment load imbalance,and serious production related profit loss.Therefore,the optimization of the task sequencing becomes the key issue for the flexible production line scheduling [22].

Table 1 Closely related literature on the reconfigurable production line scheduling
Intelligent algorithms are regarded as an effective remedy for complex scheduling problems,such as the genetic algorithm (GA),particle swarm optimization (PSO),and the ant colony (ACO) algorithm.Multi-objective PSO (MOPSO) is an intelligent algorithm first proposed by Moore and Chapman [23],which can effectively solvecomplex scheduling problems.However,the existing MOPSO has a weak global search capability,and is easy to fall into a local optimal state [24].In order to avoid that deficiency and solve the flexible flowshop scheduling problem,we propose an improved MOPSO algorithm based on the Gaussian cumulative distribution function (GCDF) and BM for the reconfigurable production systems.GCDF is used to fit the inertia weight of the particle velocity update,and the random motion mechanism of BM helps the particles to jump out of the local optimum,so as to improve the global search ability of the particles.
The rest of this article is organized as follows.In Section 2,we propose a new type of reconfigurable production line.An optimization model is established with respect to the characteristics of the flexible production line in Section 3.In Section 4,the traditional MOPSO is presented,which is then improved by introducing the GCDF,BM,polynomial mutation,and double-archive mechanism.In Section 5,we obtain the indicator function values based on several Zitzler-Deb-Thiele (ZDT)test functions and flexible production benchmark tests,showing the effectiveness of the proposed algorithm.Then an actual production scheduling problem of the reconfigurable production line is tackled with the improved algorithm in Section 6.The last section concludes the paper with several future research directions.
2.The physical model
As the concept of smart home becomes a trend for every household worldwide,various home appliances are embedded with control chips to suit the use of commercial electronics.Since the companies are usually SMEs with limited start-up funds available,and the demand for smart home appliances fluctuate regularly,it is an excellent application setting for the reconfigurable production line.
The new type of the reconfigurable production line is realized by freely connecting detachable production units.Fig.1(a) is a schematic diagram of a typical reconfigurable assembly line.The production unit A and production unit B could provide supports for 6-axis robotics and soldering machines,as shown in Fig.1(b) and Fig.1(c).Similarly,each production unit could be equipped with a standardized processing equipment to perform a specific processing task.Meanwhile,the same production unit could be used as a group of parallel machines to perform the same manufacturing task within the assembly line.When multiple production units are connected and coordinated with the central planning system,the workpiece could be automatically processed or assembled without manual intervention.

Fig.1 Various production units in reconfigurable assembly line
This reconfigurable production line demonstrates two essential features.First,the production line could be reorganized according to the actual working steps,avoiding the back and forth flow of work-in-process.Second,the reconfigurable production line could help adjust the configuration of production units,which leads to full use of each machine unit,thereby reducing the production cost.
The concept of the reconfigurable production line has now been fulfilled by a leading smart home appliance manufacturer named BoTai electronics.Its product line currently includes four categories,including smart WIFI sockets,smart LED lights,smart thermometers,and smart doorbells.At present,as the market expands,the company needs to respond to the highly volatile customer needs.To this end,the equipment and the facility layoutare reconfigurable to better suit the timely production process.As shown in Fig.2,the four mainstream smart home appliance products are manufactured in the reconfigurable production line according to their respective manufacturing processes.

Fig.2 Reconfigurable assembly line for different smart home appliances
3.The multi-objective optimization model
The physical model of the reconfigurable assembly line introduced in this paper could transform all sorts of production systems into a flexible flow shop.The scheduling of the flexible flow shop problem could be described as follows.There are N products to be processed or assembled on M different machine units.K working steps are needed to complete the processing.As shown in Fig.3,each step consists of several identical machine units (Unit A or Unit B).After each step is completed,the unfinished product enters the next processing step,and each product completes all the processing steps in the same order [9].Given the processing time of each workpiece on different machine units,the target is to determine the sequence of the jobs in the system.
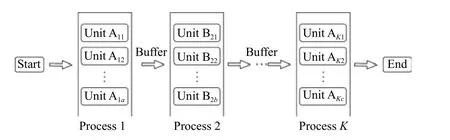
Fig.3 Flexible flowshop scheduling problem
The basic assumptions are listed below.
(i) All machines are available at time t=0,and all parts can be processed and produced at time 0.
(ii) The sequence of the processing steps of the same job type is determined.
(iii) Once the job starts processing,it cannot be interrupted until the processing is completed on the current machine.
(iv) The transportation time between two consecutive processing stages is ignored.
(v) There is no limit to the capacity of the buffer area between two consecutive processing stages.
In the actual scenario where multiple production indicators need to be considered simultaneously,a multi-objective optimization model is formulated.In order to increase the production efficiency and economic benefits,we set up four objective functions according to the actual improvement targets of the manufacturing system,namely the makespan minimization,the loss cost minimization,the total load of the machine minimization,and the number of completed orders maximization.The makespan refers to the time needed for producing one such product.The loss cost represents the sum of the processing cost,inventory cost and efficiency loss cost of all the machines.The total load of the machine denotes the total processing time of all the machines.Equations (1)−(5) are detailed mathematical expressions of the multi-objective functions.Equations (6)−(11) are the required constraints.To help the readers better capture the essence of the model,the parameters and decision variables are denoted in Table 2.
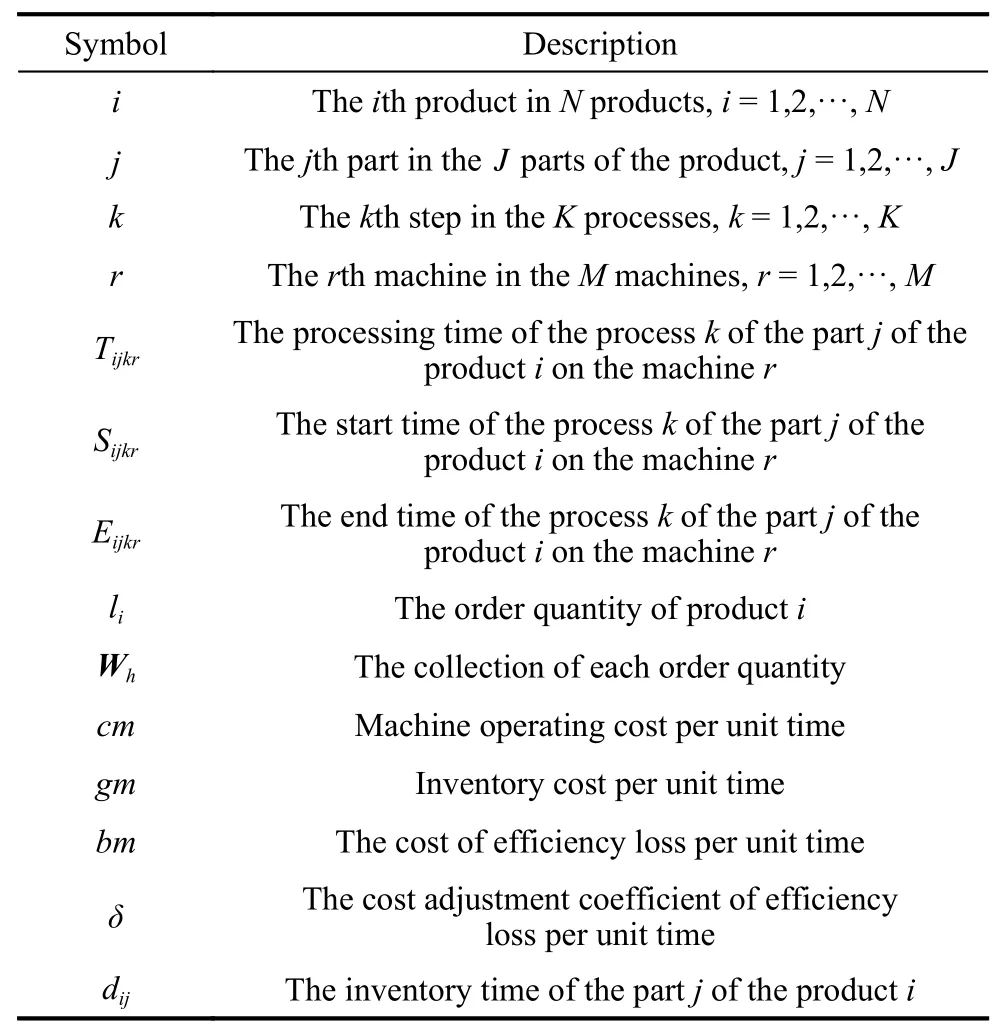
Table 2 Parameters and variables
The multi-objective functions are listed as follows.
(i) To minimize the total load of the machines

When the makespan F3is no more than the delivery date Dh,the order h is completed on time;otherwise,the delivery cannot be made on time.

The followings are the constraints of the multi-objective optimization model,
(i) Time constraints.The state of time should be nonnegative.

(ii) Resource constraints.It is assumed that only one machine could be selected for a process.
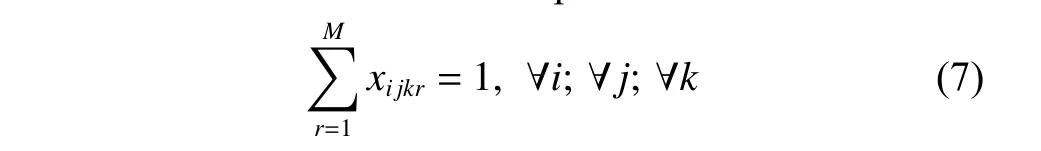
(iii) Machine-job assignment constraint.If the process k of the jth part of the product i is processed on the machine r,xijkr=1;otherwise,xijkr=0.
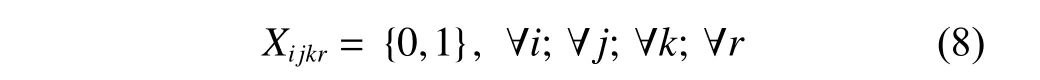
(iv) The start time of the next process of the job should be no less than the completion time of its previous processing step.
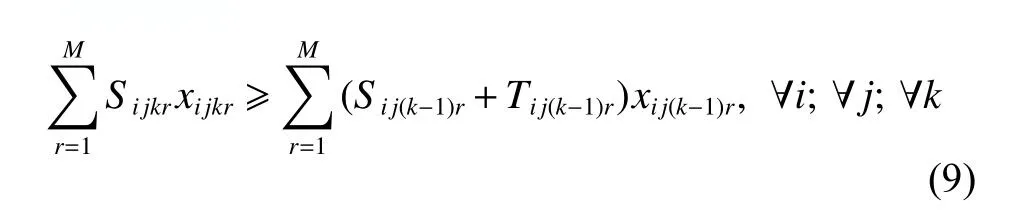
(v) The end time of any workpiece is no less than the sum of the start time,processing time and adjustment time of the workpiece.
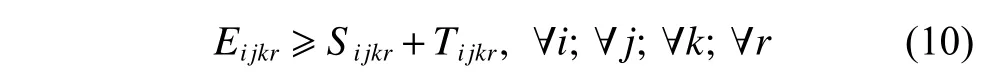
4.Standard MOPSO
The standard PSO was proposed by Kennedy and Eberhart [25]in 1995.It is a swarm intelligent optimization algorithm,which mimics the social behavior of animal herds,such as the flock of birds and the school of fish in search for food.The PSO algorithm has been successfully applied in various scheduling problems [26].It embraces advantages of simple principles,fewer parameters,and easy implementation in comparison with other swarm intelligence approaches.It has also been used to solve many complex optimization problems,which are often nonlinear [27],non-differentiable [28]and with multi-peak [29].Moore and Chapman [23]extended the PSO approach to the multi-objective optimization problem in 1999.Coello introduced external archiving and special mutation operators [30],and then formally proposed the MOPSO.With the continuous development over the years [31−33],MOPSO has now become an active method in many engineering fields [34−36].
In a typical multi-objective optimization problem,there may be different optimization objectives for different subobjective functions.The general expression is as below:
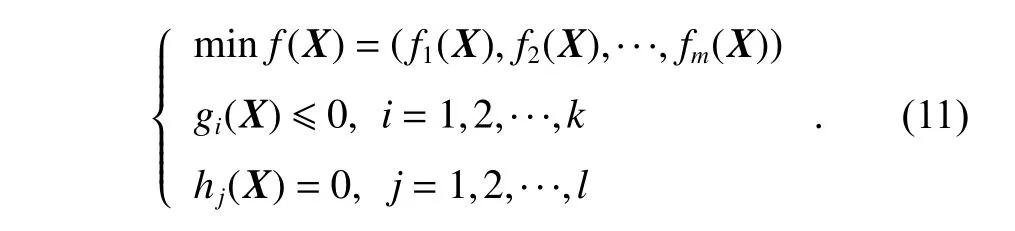
In the above formulation,the decision variables are denoted as X=(x1,x2,···,xn).In (11),m optimization goalsare considered simultaneously.The goal of this programming model is to obtain X*=(x1*,x2*,···,xn*) so that f (X*) obeys the constraints and approximates the minimum objective value.
Suppose that the MOPSO algorithm searches in the D dimension space,and a population is composed of n particles,xi=(xi1,xi2,···,xid),represents the current position of particle i,and vi=(vi1,vi2,···,vid) stands for the current velocity of particle i.pibest=(pibest1,pibest2,···,pibestd) is the current best local position searched by particle i,and gbest=(gbest1,gbest2,···,gbestd) is the best global position obtained by the entire particle swarm.In addition,the particle velocity and position update formula are presented as follows.
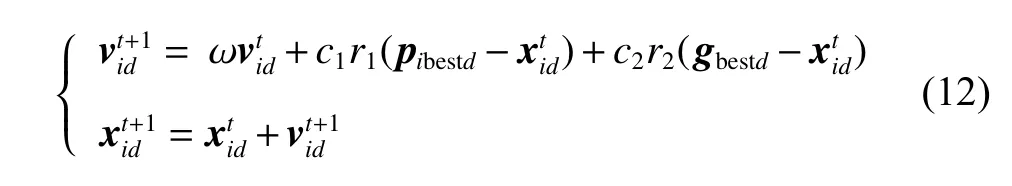
Among them,t is the current number of iterations,ω is the inertial weight,c1and c2are the learning factors,r1and r2are the random numbers in [0,1],the combination of c1and r1restricts the particle to be affected by its own factors,and the combination of c2and r2restricts the particle to be affected by population factors.
Algorithm 1The standard MOPSO procedure
Step 1Initialize a particle population XNso that each particle has a random position and a random velocity.Set the required basic operating parameters c1,c2,the maximum number of iterations MaxIter and inertia weight ω.Let iter=0,obtain the objective value with respect to each particle,then add the non-inferior solutions to the external archive,and obtain the non-inferior solution archive A.
Step 2Determine the initial local leaders and global leaders.
Step 3Update the position and velocity of all particles based on (12),and update local leaders
Step 4Maintain the external archives based on the new non-inferior solutions to form external archives for the next iteration and select global leaders
Step 5iter=iter+1,if the termination condition is satisfied or the maximum number of iterations is reached,the global optimal position and fitness values are output.Otherwise,go to Step 3.
4.1 Improved PSO with GCDF
In the standard MOPSO,the role of the inertial weights ω is to maintain the inertia of the particle motion,and to balance the global search and local search capabilities of the algorithm.If a large inertia weight is set,there is a strong global search capability and a fast convergence speed,but the local search capability is weakened,and the solution accuracy is compromised.Otherwise,if the inertia weight is small,it has a strong local search capability and good solution accuracy,but the global search capability decreases,and it tends to fall into the local optimum.This shows that the adjustment of the inertia weight could directly affect the performance of the algorithm.It is demonstrated that the overall decreased inertia weight will help the MOPSO obtain the approximate range of the solution in the early stage of the search,in the later stage it could improve the local search ability and accelerate the MOPSO convergence rate.Based on this fact,we propose a strategy for fitting ω via the GCDF.
Gaussian distribution,also known as normal distribution,is one widely applied continuous random distribution.The general probability density function of the Gaussian distribution is as follows:
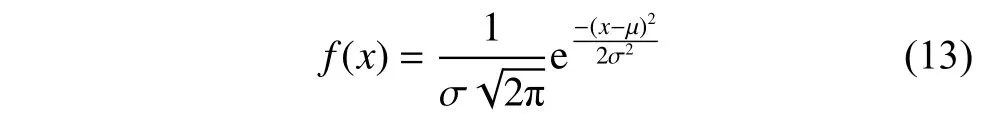
where x is a random variable,μ is the position parameter of the Gaussian distribution,and σ describes the degree of dispersion in the Gaussian distribution.Gaussian mutation has been proven to be an effective way to improve the PSO [37].Lee et al.[38]updated the velocity formula with Gaussian mutation,but only replaced the uniform random number in the velocity formula with a Gaussian random number.Higashi et al.[39]proposed a PSO with Gaussian mutation,which generates an ambiguity value from Gaussian mutation during particle iteration.In recent years,the GCDF gradually attracts the attention of researchers.The form of GCDF is shown as below:
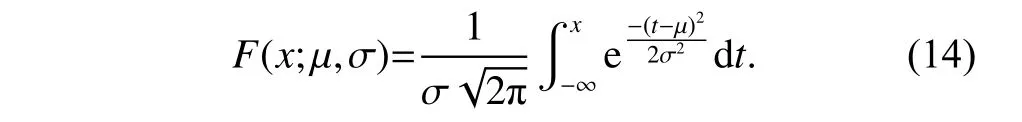
Han et al.[40]applied the GCDF to map the probability model of the compact genetic algorithm,which improves the evaluation ability of the algorithm.The present study combines GCDF and MOPSO to propose a new MOPSO improvement strategy,referred to as GCDFMOPSO.The core of GCDF-MOPSO is to construct a piecewise function to control the inertial weights based on GCDF.Extensive testing validates the effectiveness of this strategy by showing that the convergence rate and the overall performance are improved significantly.The test process is demonstrated in Section 4,and the improved formula of ω is as below:
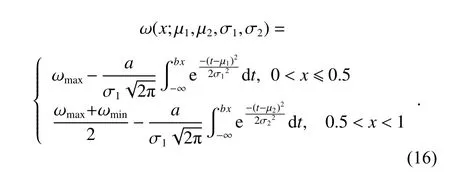
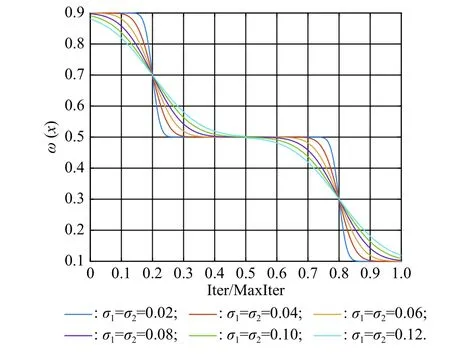
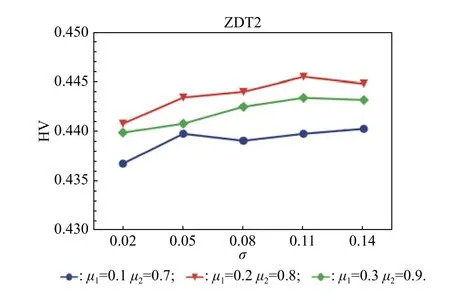
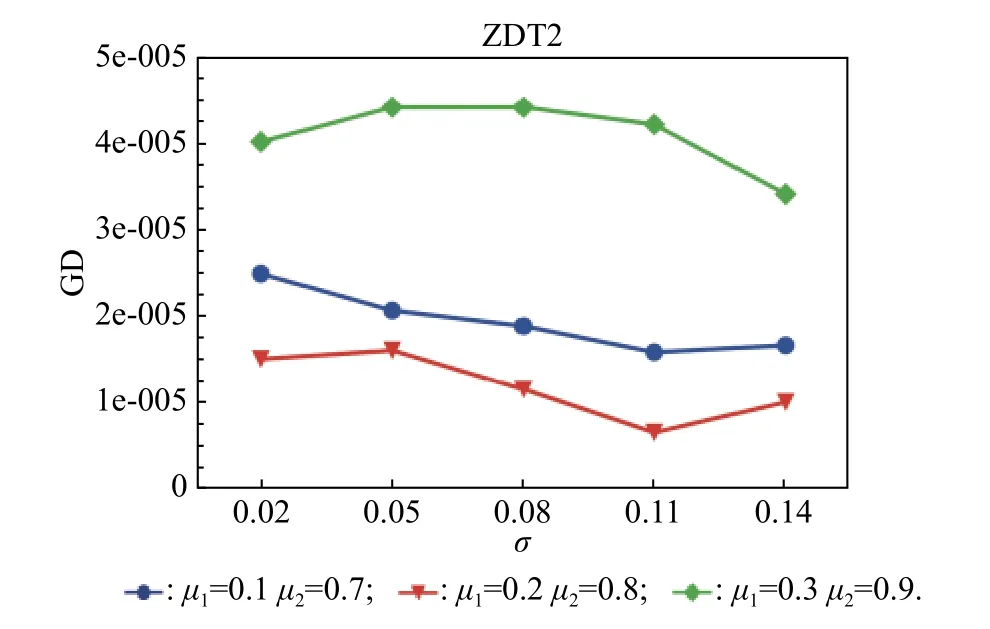
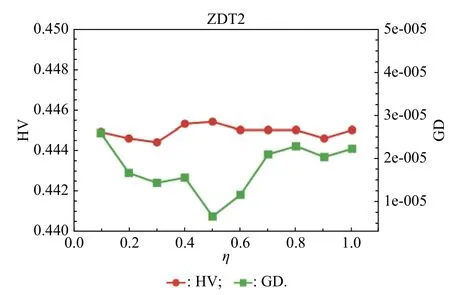
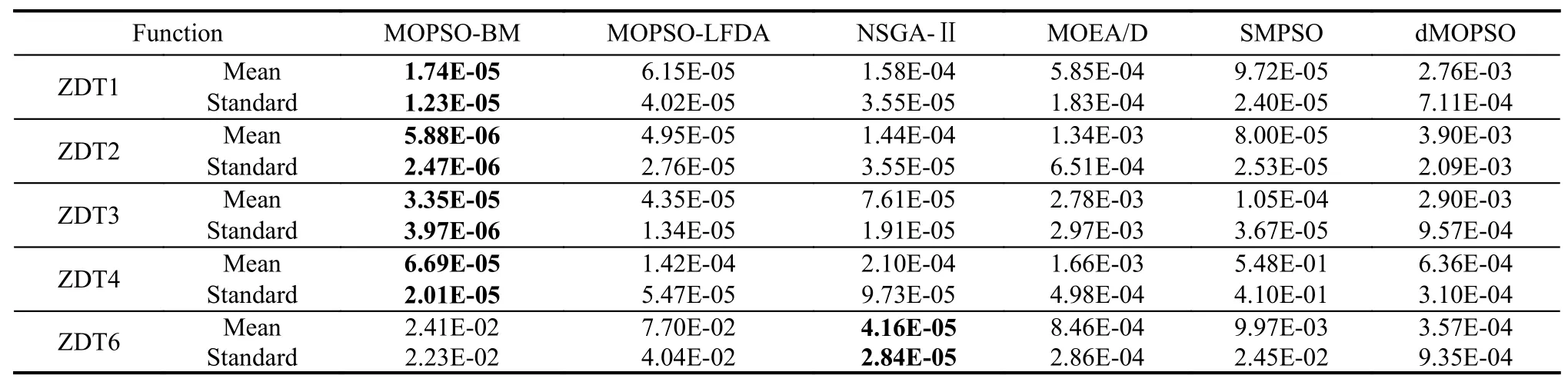
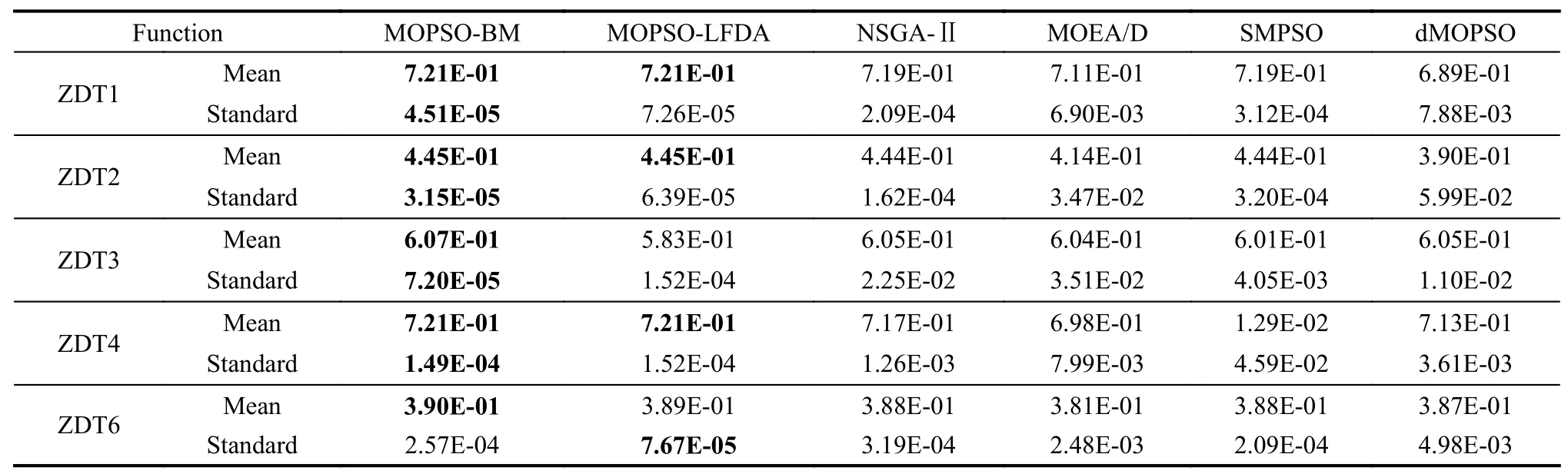
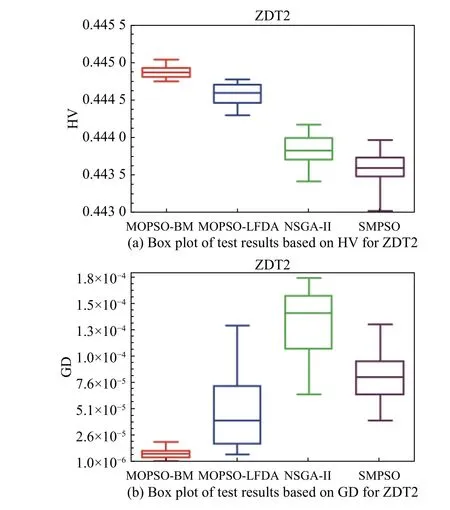
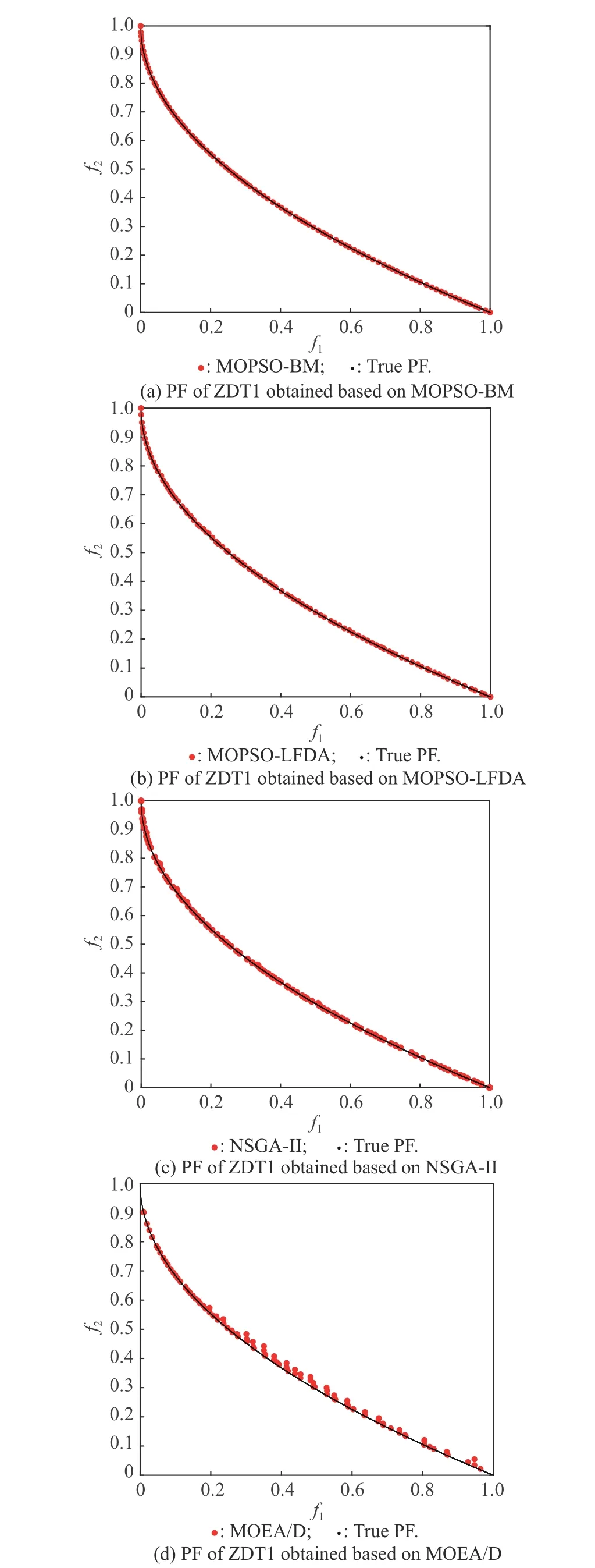
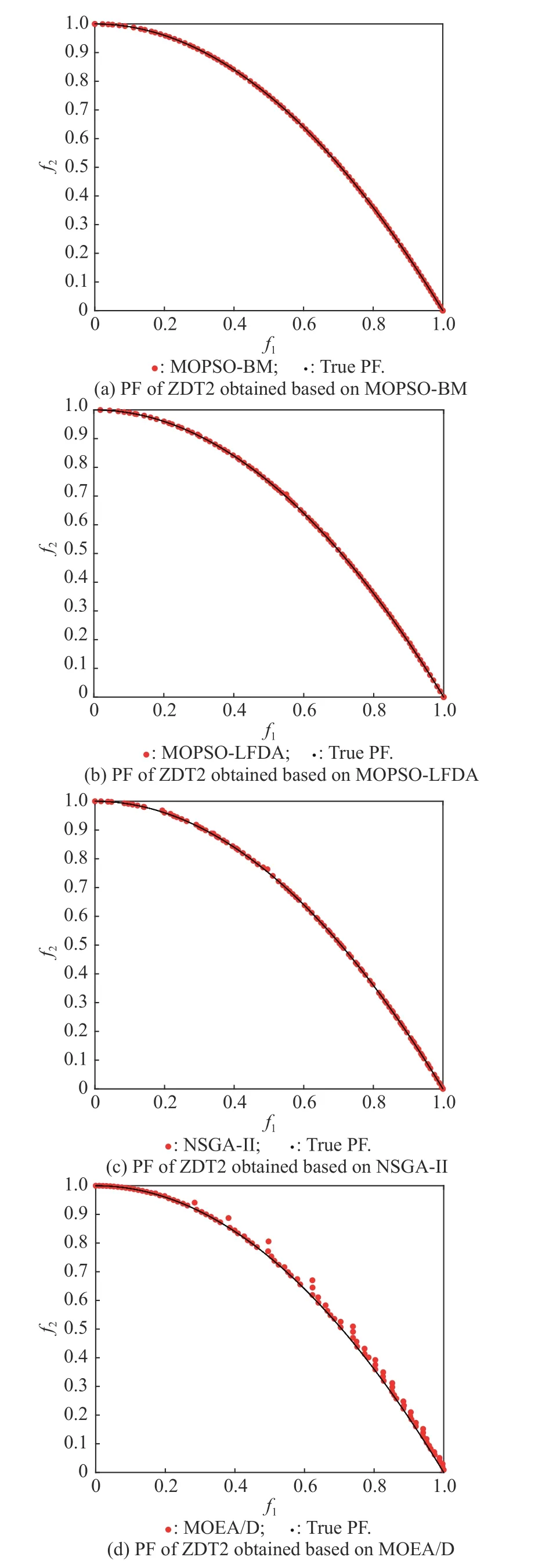
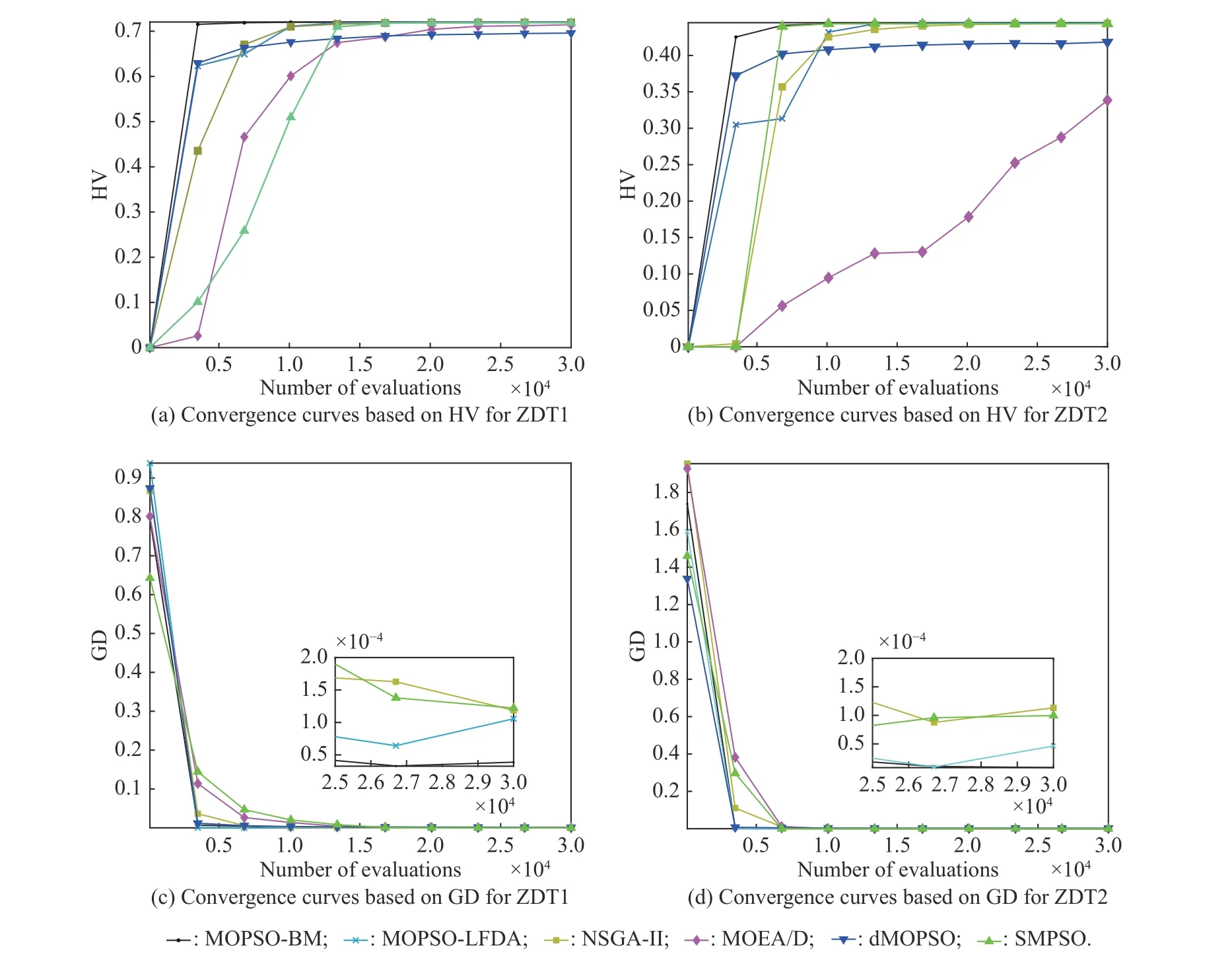
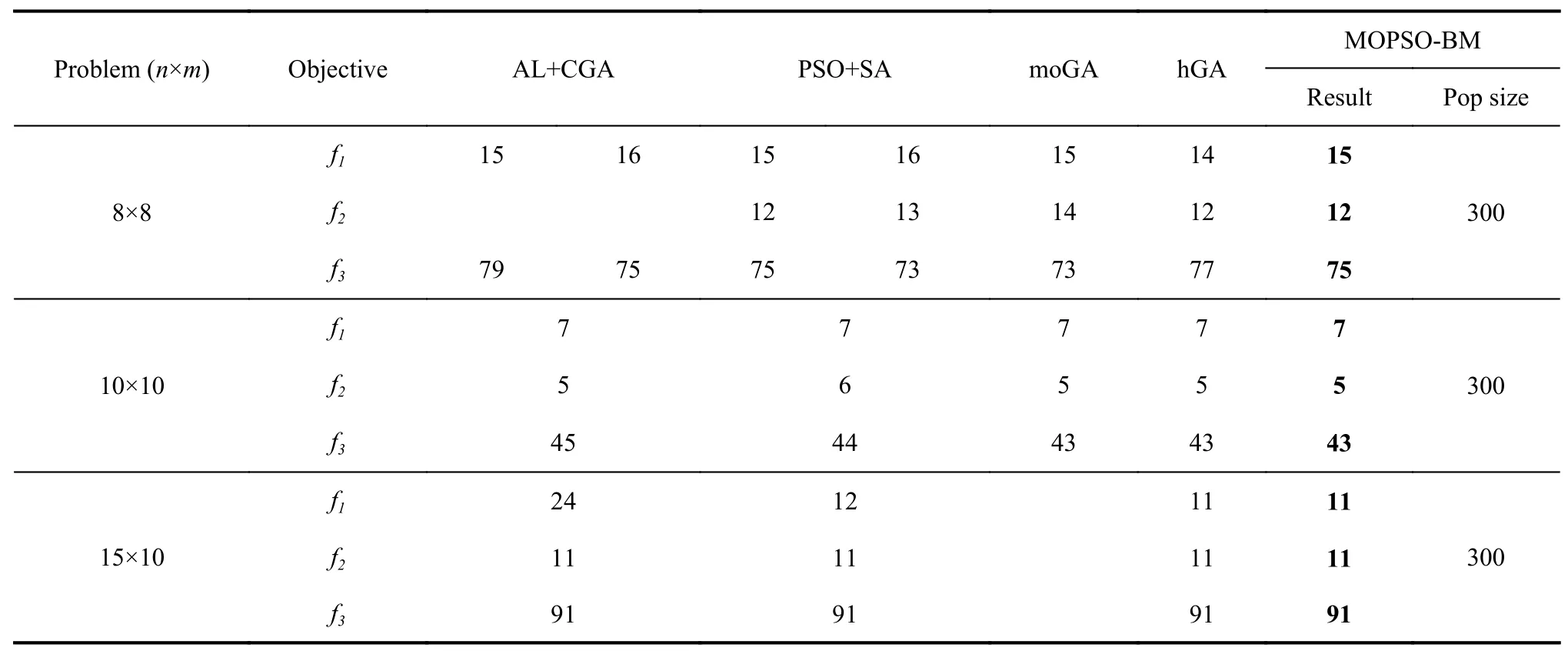
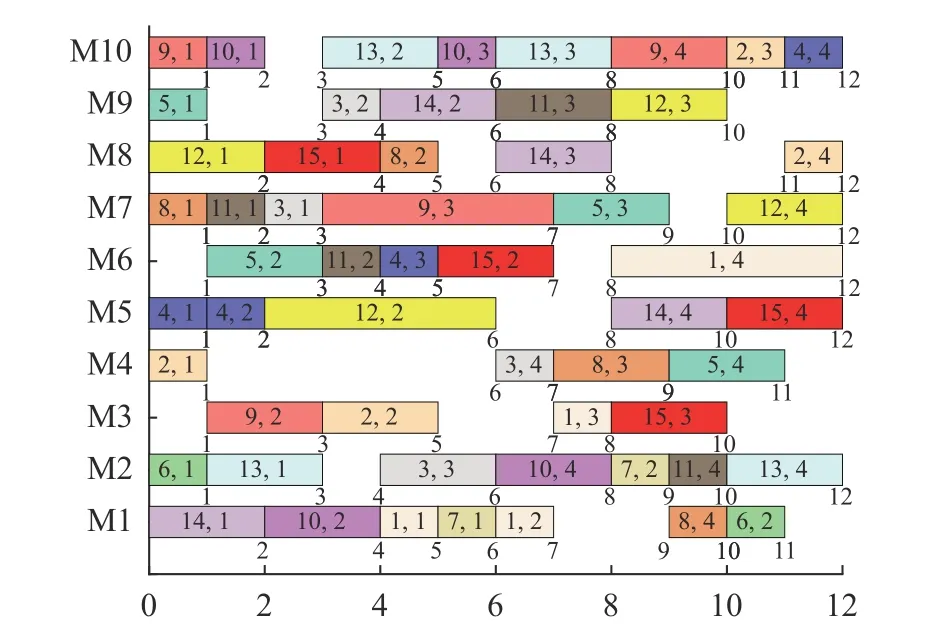
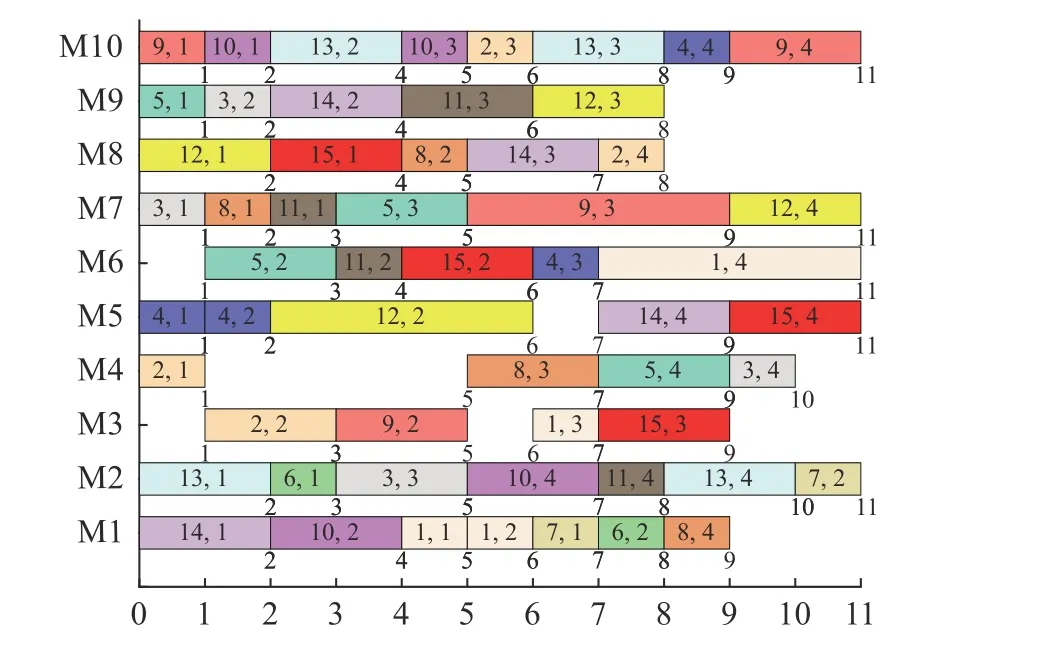
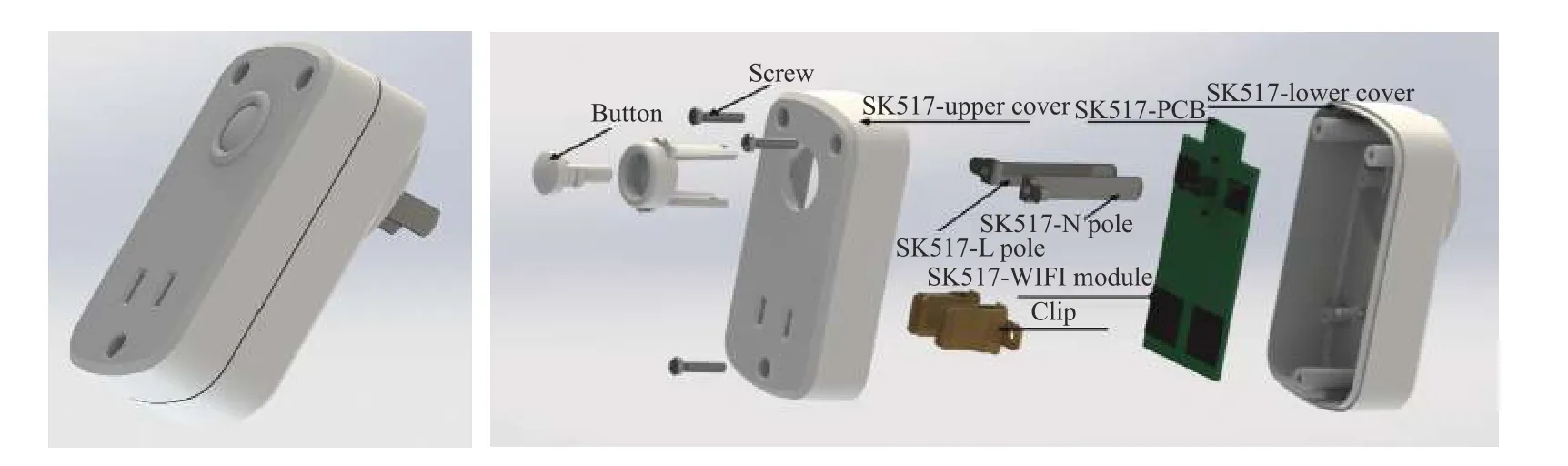
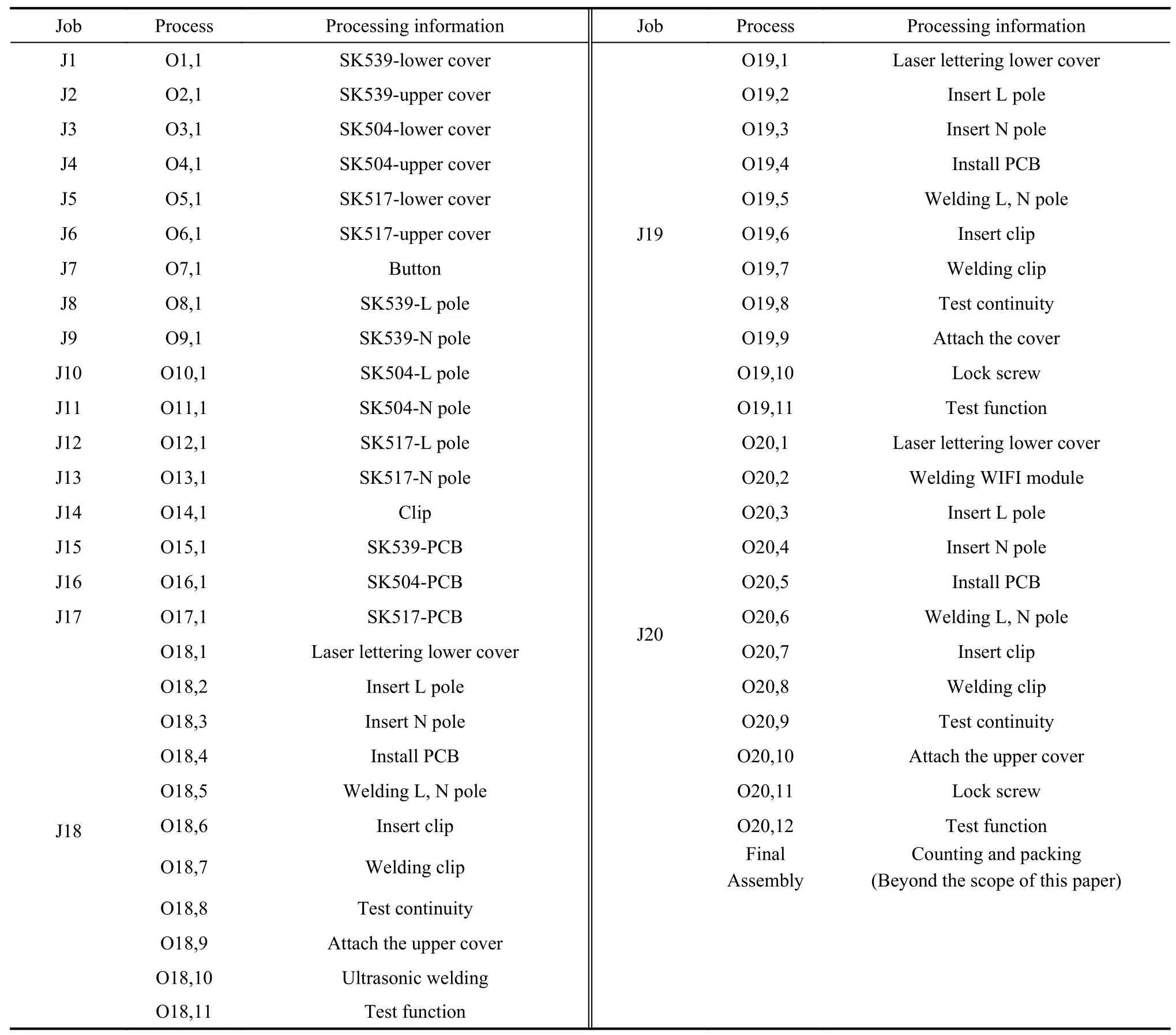
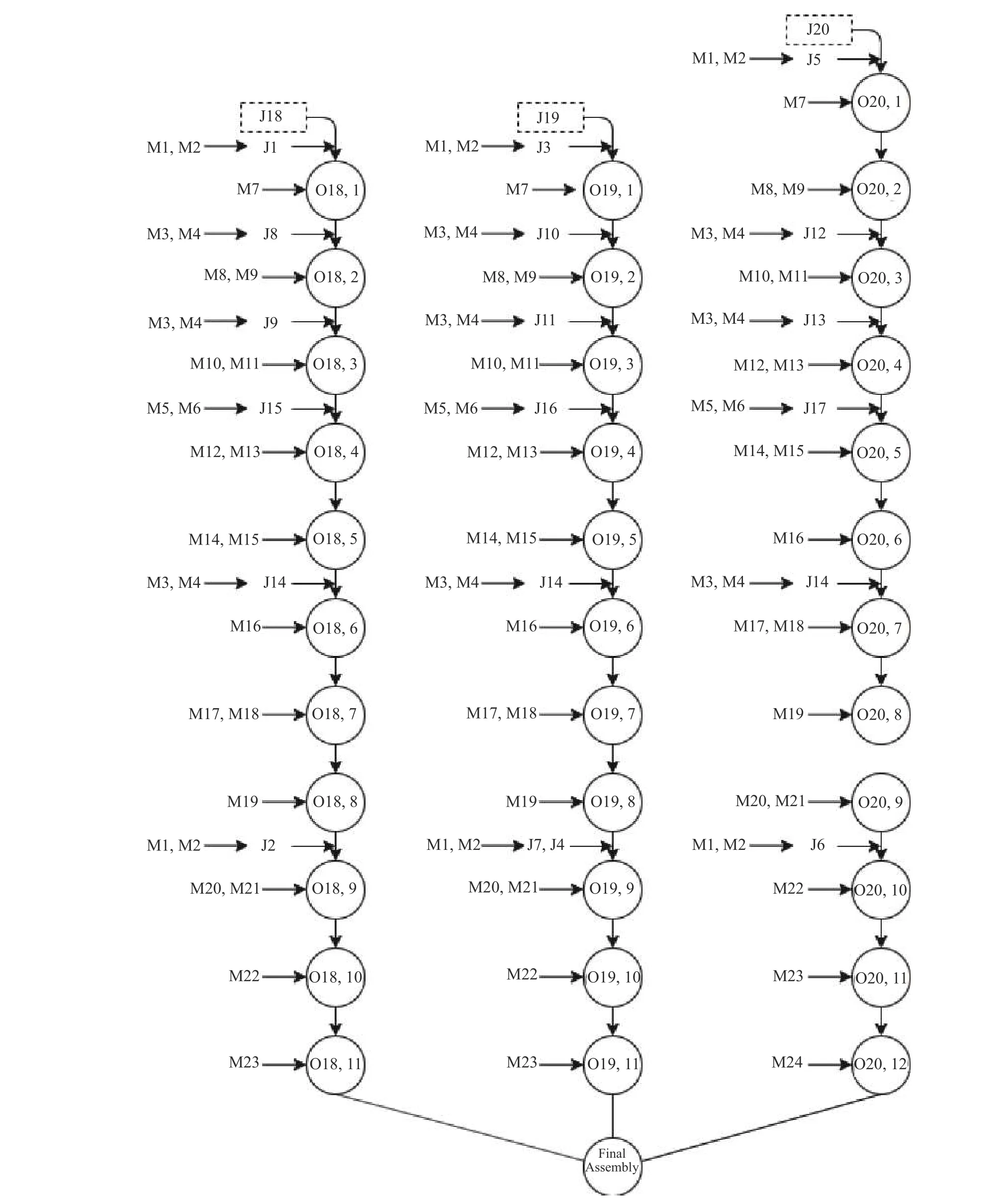
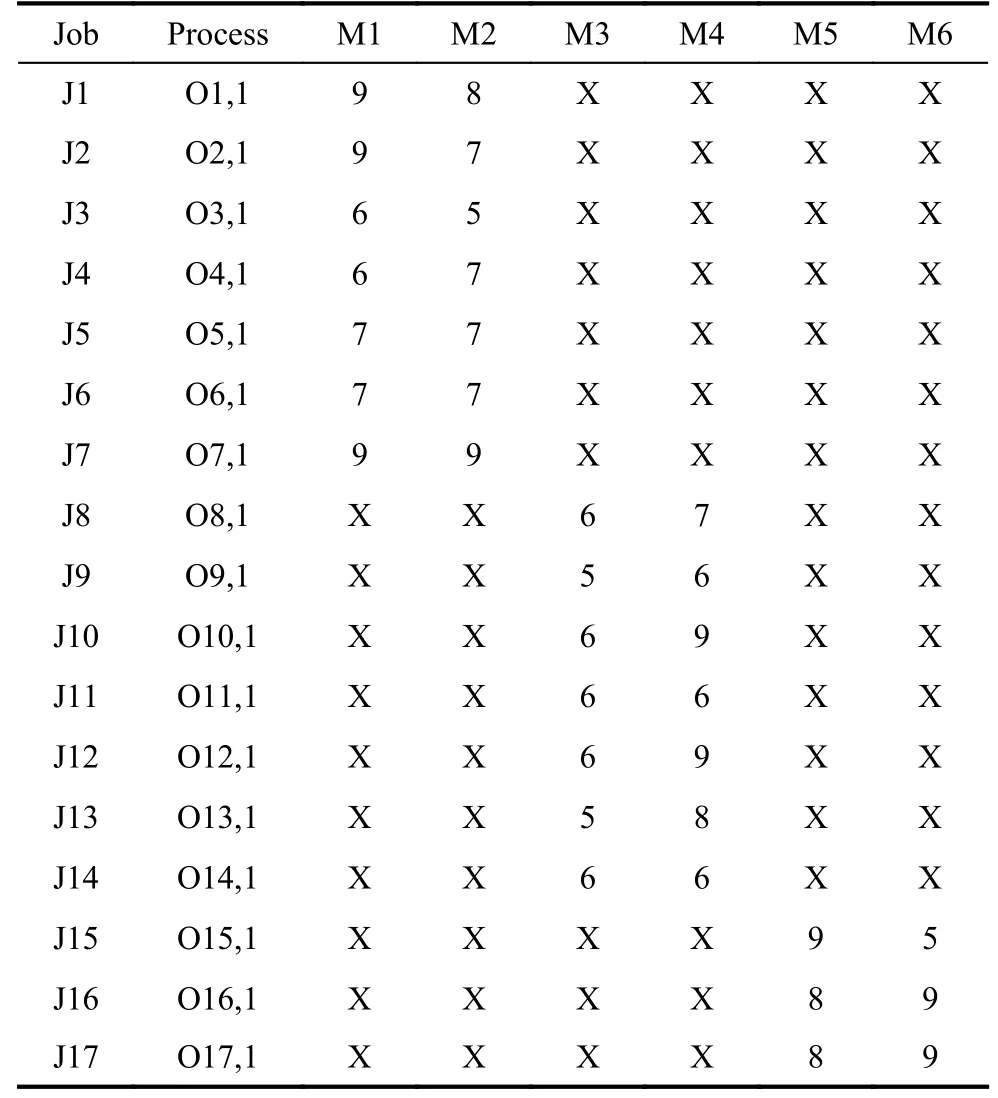
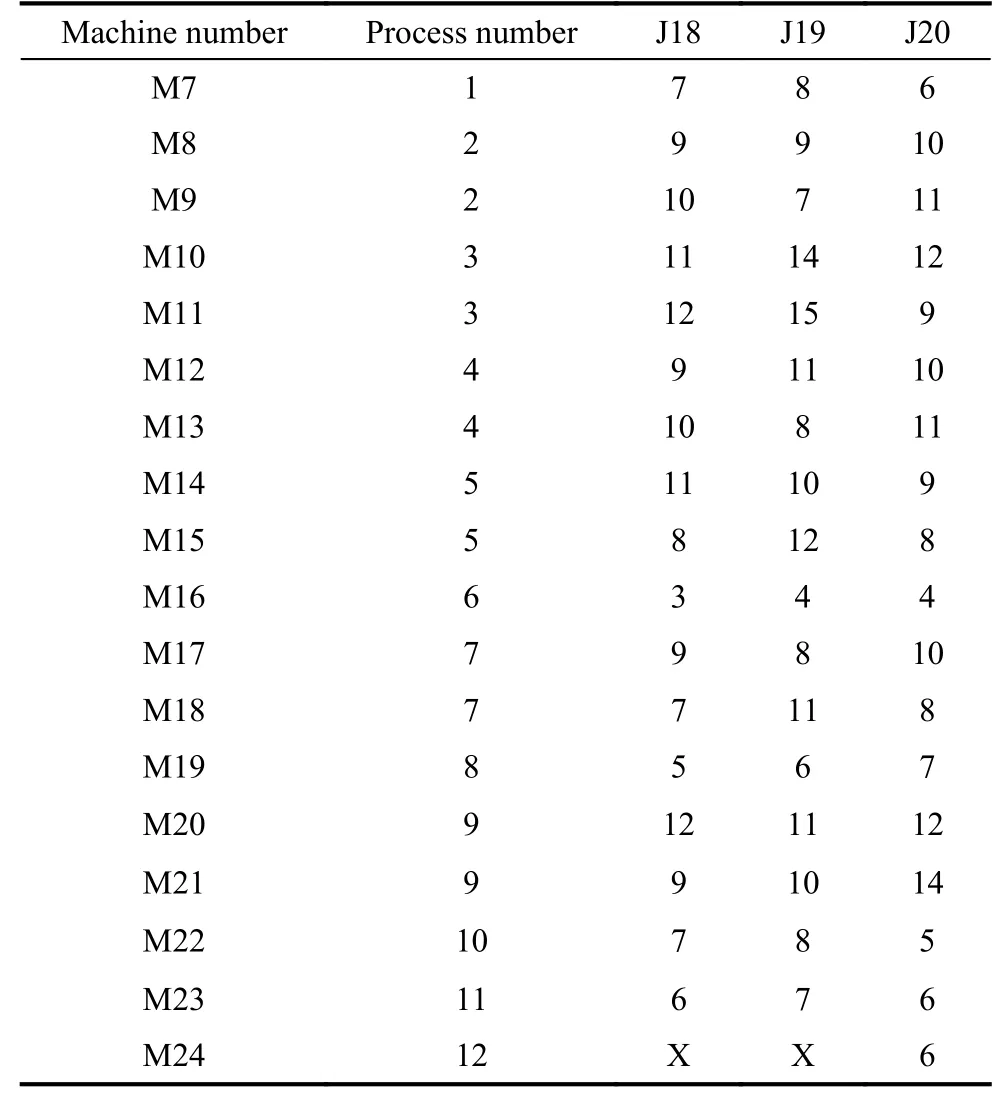
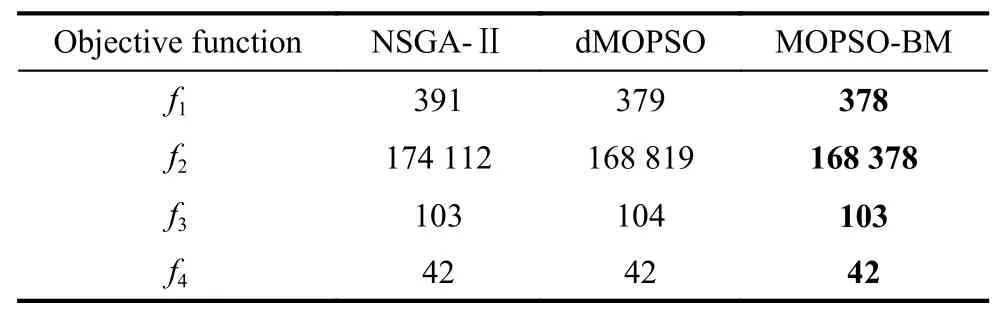
In order to find a suitable function curve which satisfies the degeneration mechanism,a large number of numerical experiments are conducted,and the results show that it is appropriate to take a=0.4,b=1,μ1=0.2,μ2=0.8,ωmax=0.9 and ωmin=0.1.Equations (15) and (16) are the improved formulae of ω in the proposed GCDF-MOPSO,where x=Iter/MaxIter.Fig.4 shows the fitting curve based on the GCDF,and it is observed that the GCDF could be divided into two stages.When 0 Fig.4 Sample curves of the GCDF The standard MOPSO algorithm bears the defect of low convergence rate while solving multi-objective problems.The particles falling into the local optimum easily is the primary cause for this problem.In order to improve this situation,the present study integrates the BM to help particles jump out of the current predicament of local optimum.Abdechiri et al.[41]proposed a Gases Brownian motion optimization (GBMO) algorithm,based on Gases Brownian motion and turbulent rotational motion.Aci et al.[42]used BM to improve the randomization stage of the dragonfly algorithm (DA).Typically,the BM is a Markovian stochastic process in continuous time and state space[43].In the range of t >0,it is with a continuous state function and a sample function.By assuming the transition process as {B(t),t≥0},the standard BM satisfies the following conditions: (i) B(0)=0; (ii) {B(t),t≥0} is an homogeneous independent smooth incremental process; (iii) For any t >0,B(t) is a random variable with Gaussian distribution,B(t)~ N(0,t); (iv) For any s Fig.5 shows the simulation trajectory after 500 steps of the BM in a 3-dimensional space with step size 1 and starting from the coordinate (0,0,0).A few studies focus on the combination of the BM and intelligent algorithms.Liu et al.[44]applied the BM to guide the search to solve the multidimensional knapsack problem (MKP).In the economic dispatch optimization problem,Han et al.[45]proposed a diffusion particle optimization (DPO) based on the diffusion mechanism of BM.In theory,a random walk can be defined as XN+1=XN+BN[42],where XNis the solution of step N,and BNis a random vector.The random motion mechanism of BM can effectively help the algorithm to jump out of the local optimum,which could better improve the overall performance of the algorithm,and enhance the search ability in an uncertain environment.where η is the control coefficient of the random variable.For the reconfigurable production line scheduling problem,with an extensive set of numerical tests,we believe that η=0.5 is recommended for the setting. Fig.5 Simulation of BM The MOPSO-BM proposed in the present paper uses the special mutation operator proposed in [30].This method ensures that every decision variable is explored in the global scope,and it can effectively improve the exploration ability of the algorithm,while avoiding premature convergence in some optimization problems. To further enhance the search capability of the algorithm,we have also employed the double-archive mechanism proposed in the MOPSO-Lévy flight and double-archive(MOPSO-LFDA) [24].In the double-archive mechanism,unlike the traditional archive method,where the particles with a small crowding distance are directly deleted when the main archive is full,the particles with a small crowding distance are put into the secondary archive.With the additional archive,more particles are retained,which prevents some particles from being deleted by mistake.It is shown that the mechanism could greatly improve the diversity of the solutions. Algorithm 2MOPSO-BM Step 1Initialize a particle population XNso that each particle has a random vector position and a random vector velocity.Set the required basic operating parameters c1and c2,the maximum number of iterations MaxIter,and the inertia weight ωmax,ωmin.Let iter=1,calculate the objective value in accordance with each particle,then add the non-inferior solutions to the external archive,and obtain the non-inferior solution archive A. Step 2Determine the initial personal leaders and global leaders,based on the crowding distance of the particles in archive A. Step 3For iter to MaxIter (i) Select the global leaderbased on the crowding distance of the particles in archive A. (ii) Update the velocity and position of particles according to (18). (iii) Implement the adaptive polynomial mutation strategy. (iv) Evaluate the particles according to the objective values. (v) Update the external archive based on the doublearchive mechanism. (vi) If the ending criterion is met or the maximum number of iterations is reached,then output the global optimal position and fitness values. The main computational cost of MOPSO-BM and MOPSO involves the iterative process of updating the position information and velocity information of the particles.Let us analyze the computational complexity of MOPSOBM in detail.According to the MOPSO-BM algorithm flow,it can be seen that Step 3 has the largest calculation cost.Step 3(i) of MOPSO-BM needs to calculate the crowding distance of all particles in archive A and sort them,which requires O(n2) operations.Step 3(ii) and Step 3(iii) require O(n) operations.In Step 3(iv),it is necessary to calculate the fitness according to the objective function.The calculation complexity depends on the complexity of the function f(n),which is O(f(n)).In Step 3(v),the double-archive mechanism requires O(n2).Combining the number of iterations MaxIter and dimension D and comprehensively analyzing the above steps,the computational complexity of MOPSO-BM is O(Max-Iter·D·(n2+f(n))). In order to verify the effectiveness of the algorithm proposed in this paper,benchmark test functions are employed in this section.In the process of running the algorithm,the number of population particles and the number of iterations are selected according to the complexity of the function.Furthermore,each function is tested multiple times to eliminate randomness.Here we use ZDT1,ZDT2,ZDT3,ZDT4 and ZDT6 introduced by Deb for testing (see Table 3) [46].In the algorithm comparison tests,we also employ three groups of the testing data,from Kacem et al.[47,48]and Xia and Wu [49].In the mentioned works,the production line is of partial flexibility,while the problems studied here are with full flexibility. The concept of generational distance (GD) is first introduced by Veldhuizen and Lamont [50],and it is used to measure the distance between the calculated Pareto frontier (PF) and the true Pareto frontier (True PF).GD is defined as in (19).P* is a set of uniformly sampled solutions on True PF,and S represents the solution set PF of the multi-objective optimization algorithm.Dist(x,P*)stands for the Euclidean distance between the closest individuals from x∈S to P*,and |S| is the cardinality of set S.It is apparent that the smaller the GD value,the better the convergence of S,and the closer it is to True PF. Table 3 Multi-objective benchmark function-ZDT series Hypervolume (HV) [51]is proposed for comprehensive evaluation of the convergence and diversity.Given a set of preset reference points r*=(r1*,r2*,···,rm*) distributed in the target space,and a set of PF obtained by the algorithm,where r* is dominated by all the solutions in S.HV measures the volume of the target space dominated by S with r* as the boundary,and its definition is shown in (20),where VOL(·) represents Lebesgue measure.It is observed that the larger the HV value,the closer S is to True PF. As for the parameter setting of MOPSO-BM in Table 4,the overall preference is more conducive to solving multiobjective optimization problems.c1and c2are the acceleration coefficients of the particles,which are usually set to 2.0,but it has been found through testing that for the MOPSO-BM,a set of 1.5 can achieve a better overall performance.The flowchart of the MOPSO-BM algorithm is shown in Fig.6. The parameters of MOPSO-BM include a,b,μ1,μ2,σ1,σ2and η,among which μ1,μ2,σ1,σ2and η are key parameters that can be adjusted and used,and their value ranges are 0.1≤μ1≤0.4,0.6≤μ2≤ 0.9,0.02≤σ1≤0.14,0.02≤σ2≤0.14,0≤η≤1.In addition,a=0.4 and b=1 are determined,and the test shows that other values of a and b may cause the algorithm not to converge.Based on ZDT2,the key parameters of the MOPSO-BM are tested in detail on the PlatEMO.It can be seen from Fig.7,Fig.8 and Fig.9 that when μ1=0.2,μ2=0.8,σ1=σ2=0.11,and η=0.5,a smaller GD and a larger HV are obtained.Therefore,these parameter settings are recommended,which can enable the algorithm to obtain a better convergence and overall performance. Table 4 Parameters settings for different algorithms Fig.6 Flowchart of the MOPSO-BM algorithm Fig.7 Factor level trend (a) Fig.8 Factor level trend (b) Fig.9 Factor level trend (c) Based on the ZDT series of test functions,we test and compare several latest MOPSO algorithms with the one proposed here,including MOPSO-BM,MOPSO-LFDA[24],NSGA-Ⅱ [52],multi-objective evolutionary algorithm based on decomposition (MOEA/D) [53],speed-constrained multiobjective PSO (SMPSO) [54],decomposition-based multi-objective PSO (dMOPSO) [55].MOPSO-LFDA is an improved algorithm proposed by Guan and Han,based on Lévy flight and double-archive mechanism.Lévy flight expands the search range of the particles and improves the probability of particles jumping out of the local area.The double-archive mechanism keeps as many particles as possible.The improved algorithm proposed in this paper also employs the double-archive mechanism,so it is necessary to compare the performance of MOPSO-BM and MOPSO-LFDA. In the numerical experiments,in order to ensure the comparability of the data,uniform parameters are assumed.The number of particle populations is set to 100,and the maximum evaluation is set to 30 000.Table 4 describes the detailed parameters of all the listed algorithms,which are run on the PlatEMO [56].The parameter setting of MOPSO-BM in Table 4 refers to Subsection 5.2,and the parameters of other algorithms refer to MOPSOLFDA.These settings allow for a better comparison. All the algorithms are independently run 30 times to take the mean and standard deviation for the comparative analysis.The computing platform is built with Matlab R2018b,Intel(R) Core (TM) i7-7700 CPU @3.60 GHz,16 GB RAM. Table 5 shows the GD obtained by solving the ZDT function using different algorithms.The smaller the GD value,the better the convergence performance of the algorithm.For ZDT1−ZDT4,the average and standard deviations of GD obtained by the proposed MOPSO-BM are the smallest.The results show that MOPSO-BM has excellent and stable convergence performance for ZDT1−ZDT4 functions.For ZDT6,NSGA-Ⅱ has the best performance. Table 5 Test results of the GD based algorithms Table 6 shows the HV obtained by using different algorithms to solve the ZDT function.The larger the HV,the better the overall performance of the algorithm.Both MOPSO-BM and MOPSO-LFDA obtain a higher HV.However,through comparison,it is found that for ZDT1−ZDT4,the standard deviation of MOPSO-BM is smaller,indicating that the stability of MOPSO-BM is better. Table 6 Test results of the HV based algorithms Fig.10 shows that MOPSO-BM can obtain a better mean and smaller fluctuations compared with other algorithms. Fig.10 Box plots of test results based on HV and GD Fig.11 and Fig.12 show the comparison between PF and True PF.Fig.13 shows the convergence ability of different algorithms.It can be seen that the convergence ability of MOPSO-BM is outstanding.Table 7 shows the results of multiple algorithms on the flexible production scheduling problem.The Xia and Wu data set contains three test problems from Kacem et al.[47,48]and Xia and Wu [49]. The three objective functions [48]aref1,f2,f3,wheref3represents the total processing load of all the machines.Wkstands for the load of a single machine among all the machines.f2demonstrates the maximum load of a single machine among all the machines. The approach by localization and the controlled genetic algorithm (AL+CGA) algorithm was proposed by Kacem et al.[47,48],the PSO+SA algorithm was proposed by Xia and Wu [49],the multistage operationbased genetic algorithm (moGA) algorithm was proposed by Zhang and Gen [57],and the hybrid genetic algorithm (hGA) was proposed by Gao and Sun et al.[58].Table 7 lists the optimal results of all the algorithms after five runs.It is observed that in searching for a better objective function value,the performance of MOPSO-BM is outstanding.Fig.14 is a Gantt chart obtained by solving a 15×10 problem via PSO+SA.Fig.15 is also a Gantt chart plotted via solving the same sized problem via MOPSO-BM.The vertical axis of the Gantt chart represents the equipment number,and the horizontal axis stands for the processing time.The number in the Gantt chart indicates the workpiece number and the process number.For example,“2,1”represents the first process of the second workpiece.Besides,the same color indicates the same workpiece. Fig.11 PF and True PF of four algorithms for ZDT1 Fig.12 PF and True PF of four algorithms for ZDT2 Fig.13 Convergence curves of different algorithms Table 7 Scheduling results for different algorithms on the Xia and Wu datasets By comparing and analyzing Fig.14 and Fig.15,it is discovered that the makespan obtained by MOPSO-BM is smaller than that by PSO+SA,which validates that the MOPSO-BM scheduling scheme can provide the production schedule with a high efficiency.Second,it can be seen from Fig.15 that M10,M7,and M2 will run at full load,effectively reducing the machine idle time.In comparison,the scheduling outcome in Fig.14 suffers from more machine idle time and a lower resource utilization. Fig.14 Gantt chart for 15×10 problem solved via PSO+SA (f1 =12,f2 =11,f3 =91) Fig.15 Gantt chart for 15×10 problem solved via MOPSO-BM(f1 =11,f2 =11,f3 =91) For an actual manufacturing plant responsible for smart home appliances,the reconfigurable assembly line in the mixed workshop processes three products at the same time,including parts processing and assembly.The models of the three smart sockets are SK539,SK504 and SK517,which are shown as detailed bill of materials in Fig.16,Fig.17,and Fig.18,respectively.The detailed process and part processing information is listed in Table 8. Fig.16 Bill of materials for SK539 Fig.17 Bill of materials for SK504 Fig.18 Bill of materials for SK517 Table 8 Processing information for the jobs with respect to equipment In Table 8,the processing information of the three smart sockets SK539,SK504 and SK517 are demonstrated.Here we will use MOPSO-BM to solve the scheduling problem based on the three products on the reconfigurable flexible assembly line.“J1”means part 1,and“O1,1”stands for the first processing route of part 1.Table 9 presents the processing machine information located in the workshop.Fig.19 reflects the sequence constraints of each processing procedure.Table 10 and Table 11 show the processing time required for all the processing steps on each equipment.“X”means that this step cannot be processed on this machine.It can be also seen from Table 10 and Table 11 that this production workshop adopts a partially flexible production method. Table 9 Machine information in the flexible production line Fig.19 Flow chart of the processing sequence for different jobs To test and compare the three different algorithms,namely,the NSGA-Ⅱ algorithm,the dMOPSO algorithm and the MOPSO-BM algorithm,Table 12 lists the parameters used in all the algorithms.The solution results via the three algorithms are obtained in Table 13.The test results demonstrate that the MOPSO-BM algorithm can obtain more reasonable scheduling results under the same testing environment,and can achieve lower cost losses under the same order quantity and the minimum makespan. Table 10 Processing time of each process (a) s Table 11 Processing time of each process (b) s Table 12 Parameters settings in different algorithms Table 13 Comparative results of the scheduling problem with the three algorithms In the context of flexible intelligent manufacturing,the production units with various functions are integrated and reconfigured to cater the ever-changing customer demands.Starting from actual production,this paper proposes a new reconfigurable production line solution,which can help SMEs improve machine utilization and reduce production cost.For a typical reconfigurable assembly line,we establish a multi-objective optimization model to minimize the makespan,loss cost,and the total load of the machine,and in the meantime to maximize the number of completed orders.The conventional MOPSO is prone to be trapped in the local optimum due to its weak global search capability.To effectively tackle the multi-objective scheduling problem,an improved MOPSO algorithm is proposed based on GCDF and BM.The random motion mechanism of BM is combined with the MOPSO to effectively alleviate the weakness of the traditional algorithms.By using the piecewise GCDF to fit the inertia weight strategy,we could balance the global search ability and convergence rate of the algorithm during the iterations,and the solution quality could be improved as well. Based on the evaluation indicators GD and HV,we test and compare the proposed MOPSO-BM algorithm with the other five latest multi-objective intelligent algorithms,for the benchmark functions from ZDT1 to ZDT6.The test results show that MOPSO-BM performs better in terms of convergence speed and solution quality.Besides,the proposed MOPSO-BM algorithm is tested on three benchmark problems of flexible flow shop scheduling,which validates the effectiveness of the algorithm.For a real case of the reconfigurable production line for smart home appliances,two latest algorithms,NSGA-Ⅱ and dMOPSO as well as MOPSO-BM,are employed to tackle the scheduling problem.The comparison results indicate that the MOPSO-BM algorithm outperforms the other two when dealing with such reconfigurable production line scheduling problems.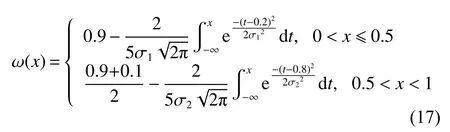
4.2 Improved PSO with BM
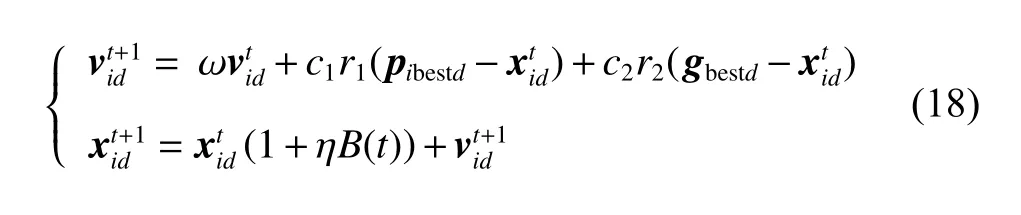
4.3 Mutation operation
4.4 Double-archive mechanism
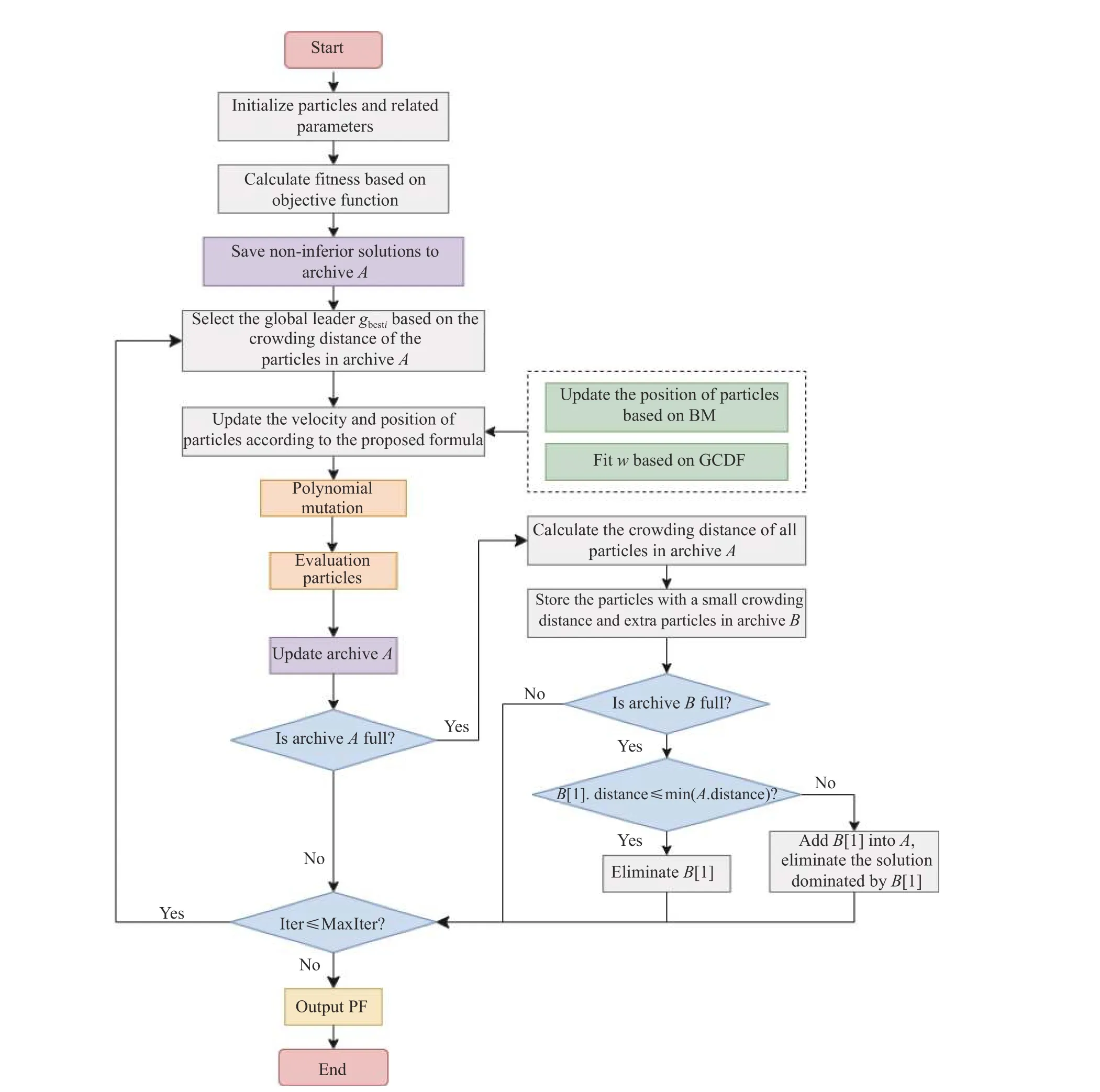
4.5 The MOPSO-BM algorithm
5.Experiments on benchmarks
5.1 Test functions and evaluation index

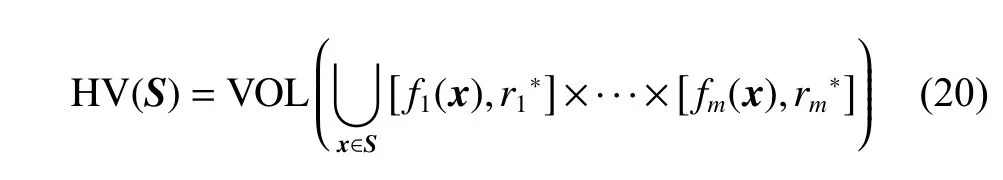
5.2 Parameter setting

5.3 Algorithm comparison
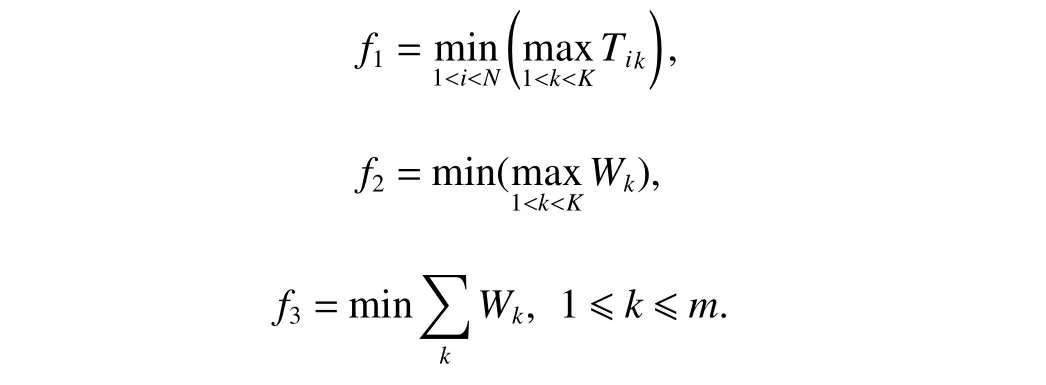
6.A case study for the smart home appliance production line



7.Conclusions
 Journal of Systems Engineering and Electronics2021年2期
Journal of Systems Engineering and Electronics2021年2期
