An efficient migrating birds optimization algorithm with idle time reduction for Type-I multi-manned assembly line balancing problem

ZHANG Zikai ,TANG Qiuhua,* ,LI Zixiang ,and HAN Dayong

1.Key Laboratory of Metallurgical Equipment and Control Technology,Wuhan University of Science and Technology,Wuhan 430081,China;2.Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering,Wuhan University of Science and Technology,Wuhan 430081,China

Abstract:Multi-manned assembly line,which is broadly utilized to assemble high volume products such as automobiles and trucks,allows a group of workers to assemble different tasks simultaneously in a multi-manned workstation.This additional characteristic of parallel operators increases the complexity of the traditional NP-hard assembly line balancing problem.Hence,this paper formulates the Type-I multi-manned assembly line balancing problem to minimize the total number of workstations and operators,and develops an efficient migrating birds optimization algorithm embedded into an idle time reduction method.In this algorithm,a new decoding mechanism is proposed which reduces the sequence-dependent idle time by some task assignment rules;three effective neighborhoods are developed to make refinement of existing solutions in the bird improvement phases;and temperature acceptance and competitive mechanism are employed to avoid being trapped in the local optimum.Comparison experiments suggest that the new decoding and improvements are effective and the proposed algorithm outperforms the compared algorithms.

Keywords:multi-manned,assembly line balancing,migrating birds optimization,meta-heuristics.

1.Introduction

The assembly line,one of the flow-oriented production systems,is widely used in the manufacturing industries to process large and complex productions such as cars and electronics. Its corresponding problem,named the assembly line balancing problem,optimizes some specific objectives by assigning a set of tasks with precedence relationships into a series of workstations.Based on the objective functions,the assembly line balancing problems can also be divided into four categories [1]:Type-I minimizes the number of workstations for a given cycle time;Type-II minimizes the cycle time for a predefined number of workstations; Type-E maximizes the line efficiency when the cycle time and the number of workstations are unknown;Type-F aims to find a feasible solution when the number of workstations and cycle time are given.These problems are proven as NP-hard problems since a bin-picking problem without involving the precedence relationships is NP-hard in the strong sense [2].

In industrial manufacturing,different conditions need to be considered in assembly line balancing problems.These new problems are named general assembly line balancing problems. The multi-manned assembly line balancing is one of the general assembly line balancing problems.Current research assumes that only one operator in each workstation assembles the tasks.However,when the assembled products are more complex,the lines would need hundreds of workstations,resulting in the increase of production costs and space occupancy.Hence,to avoid this situation,Akagi et al.[3]first proposed the multi-manned workstations and formulated the multimanned assembly line balancing problem (MALBP)where more than one operator can be assigned to each multi-manned workstation.It should be noted that if each workstation is assigned with two operators and operation direction constraints are involved,then the MALBP becomes a two-sided assembly line balancing problem.With multi-manned workstations,the space utilization increases,the production costs decrease,and thereby the line efficiency is improved [4].To our best knowledge,limited studies explore the MALBP.Hence,this paper focuses on the MALBP.

Since this work focuses on multi-manned assembly line balancing,we first investigate the latest developments of the assembly line balancing,and later present a review on MALBP.

To achieve the optimization of assembly line balancing problems,three solution procedures including mathematical programming approaches,heuristic and metaheuristic algorithms are developed [5].For mathematical programming approaches,Gokcen et al.[6]developed a goal programming approach;Sewell et al.[7]and Li et al.[8]designed a branch,bound and remember algorithm.For heuristic algorithms,Balakrishnan et al.[9]designed a single-pass heuristic;Sternatz [10]proposed an enhanced multi-Hoffmann heuristic; Li et al. [11] developed three rules including task selection,task assignment,and task exchange.For meta-heuristic algorithms,the more common and improved algorithms include the genetic algorithm (GA) [12,13],the simulated annealing algorithm (SA) [14,15],particle swarm optimization(PSO) [16],and ant colony optimization (ACO) [17].

The above research just considers one operator in each workstation;while as the scale of products increases,the assembly line needs hundreds of workstations to ensure smooth production.This situation increases the production costs and space occupancy.To improve this situation,more research begins to study the MALBP which allows some operators to work in the same workstations.

For the MALBP,Dimitriadis [18]first examined the performance of MALBP and proposed a modified heuristic procedure to minimize the workstation idle time.This approach started from the first workstation and consecutively assigned tasks into this workstation until an upper bound was reached. Later,the research about MALBP can also be divided into three categories according to the solution procedures mentioned above.

The mathematical programming approaches used in MALBP mainly include the branch and bound method[19],the benders’ decomposition algorithm [20]and the constraint programming model [21].These approaches are effective in small-and middle-scale instances.However,when the scales increase,it is difficult to solve the related problems.

Regarding the heuristics,Kellegoz et al.[22]designed a priority rule-based heuristic.Lopes et al.[23]developed a novel model-based heuristic procedure.These heuristics are convenient for implementation and can find feasible solutions quickly,but they cannot ensure that all the obtained solutions are efficient for all the instances.

For the meta-heuristics,Fattahi et al.[24]developed an ACO to solve the MALBP.Roshani et al.[25]considered the line efficiency,line length,and smoothness as the objectives of MALBP and proposed an SA to achieve the balance.Kellegoz [26]considered that some operators cannot work at the same physical location of multimanned assembly lines and further proposed a GanttSA algorithm.Chen [27]designed a new decoding mechanism and then employed the SA algorithm to solve the MALBP.In another study,Chen et al.[4]further studied the resources including machines and tools constraints in MALBP and proposed a hybrid GA algorithm to minimize the number of workstations,operators and resources.Sahin et al.[28]considered the resource investment,and adapted a PSO to solve this problem.These meta-heuristics are proved to be more effective in solving large-scale instances of MALBP.

The multi-manned assembly lines are widely used to assemble complex products such as home appliances and vehicles. However,limited research studies MALBP.Therefore,aiming at the Type-I MALBP,this paper mainly has the following contributions.

(i) A new decoding mechanism with idle time reduction is proposed to build feasible and efficient solutions.This decoding improves the quality of solutions by reducing the sequence-dependent and remaining the idle time.The final experiments prove that the proposed decoding strategy outperforms the existing decoding mechanisms.

(ii) An efficient migrating birds optimization (EMBO)algorithm is first developed for the Type-I MALBP.This algorithm designs three improvements,including multiple neighborhoods,acceptance criteria and competitive mechanism,to enhance its performance.

The remainder of this paper is organized as follows.Section 2 defines the MALBP.Section 3 demonstrates the proposed EMBO.Section 4 reports the results of the comparison experiments.Section 5 concludes the findings and suggests future avenues.

2.Type-I MALBP

For convenience,the related notation is defined in Table 1.This paper considers the Type-I MALBP,in which each task i (i=1,2,···,n) should be allocated to some multimanned workstations J (J={1,2,···,m}).For each workstation j,if this workstation is opened (Zj=1),it may be allocated with more than one operator to perform the tasks,and the admitted maximum number of operators in each workstation is umax.For each task i,it must be assigned to only one workstation and processed by only one operator.

Table 1 Description of the notation

In this paper,we aim to minimize the number of operators and workstations.As the labor costs have rapidly increased in recent years,we regard the optimization of the number of operators as the primary objective and the minimization of the total workstations as the secondary objective.Therefore,the final objective function is shown as

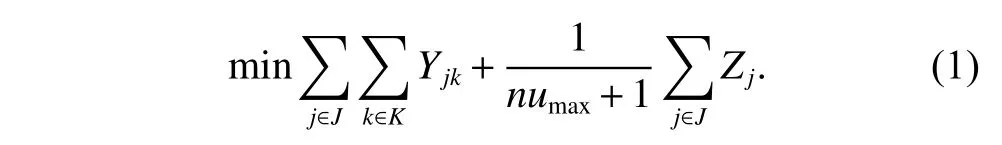
2.1 Mathematical model

The final objective function subjects to

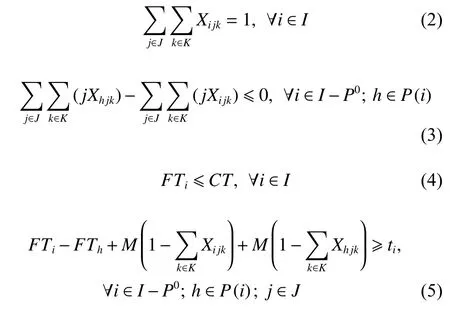
The objective function (1) points to optimize the number of laborers as the essential objective and the number of workstations as the auxiliary objective according to[24].Limitation (2) guarantees that each task is allocated precisely to one position of one worker at one workstation.Limitation (3) addresses the precedence relations.Limitation (4) is the cycle time constraint.Limitations(5)−(7) control the sequencing limitations.Limitations(8)−(10) are the operator constraints.Limitations (11)−(13) limit the variable Zj.The above limitations (8)−(13)tightly limit the decision variables.Limitation (14) addresses the minimum value of the finishing time.Limitations (15)−(18) indicate binary variables.

2.2 Illustrative example

An illustrative example with nine tasks is presented to introduce the MALBP.The precedence diagram is shown in Fig.1(a) for instance.The processing time of each task is also presented above the task node in this figure.The cycle time CT is 8 and at most three operators can work in each workstation (umax=3).

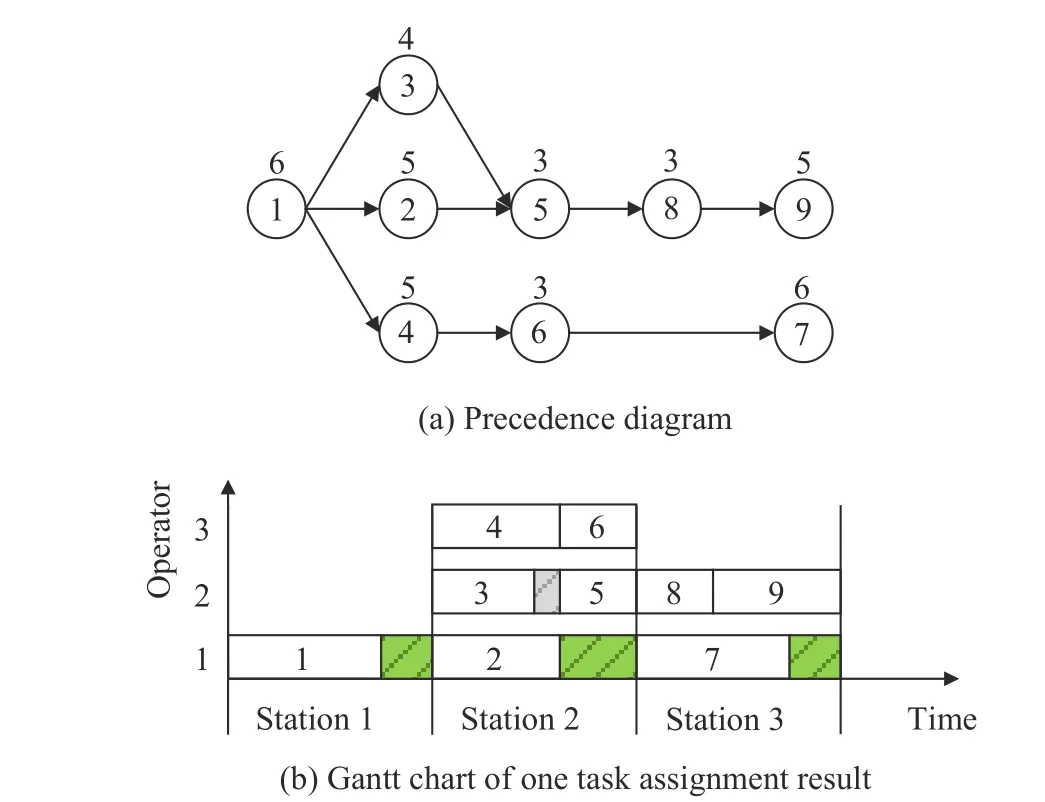
Fig.1 Illustrative example

One solution is depicted in Fig.1(b).From this figure,it can be observed that one task (task 1) and one operator are assigned to workstation 1,and five tasks (tasks 2,3,4,5 and 6) and three operators are assigned to workstation 2,and three tasks (tasks 7,8 and 9) and two operators are assigned to workstation 3,respectively.Here,there is a total of three workstations and six operators.Under the cycle time constraint,all the tasks are finished before 8 s.As stated previously,all these task assignments also should meet the precedence relation constraint.For example,task 5 cannot be assigned until their predecessor task 2 and task 3 have been completed,hence,operator 2 in workstation 2 first processes task 3 while operator 1 processes task 2 at the same time.After the completion of task 2 and task 3,operator 2 starts the procession of task 5.In a word,there is a total of six operators and three workstations. Instead,if one operator is allowed for each workstation,one of the optimal task assignment plans is:task 1 in workstation 1,task 2 in workstation 2,task 3 and task 5 in workstation 3,task 4 and task 6 in workstation 4,task 8 and task 9 in workstation 5,and task 7 in workstation 6.In this assignment plan,there are a total of six operators and six workstations.

Through the comparison of these two task assignment plans,it can be concluded that MALBP can get a better plan with fewer workstations due to the multi-manned workstations,and further saves a lot of opening-workstation costs.

Since the MALBP is a strong NP-hard problem,the optimal solution can only be obtained by the above model on small-scale instances.For this reason,heuristics need to be developed to achieve the optimization of middleand large-scale instances.Hence,this paper develops an EMBO embedded with an idle time reduction decoding mechanism.

3.EMBO algorithm

The migrating birds optimization (MBO) algorithm starts with a set of initial birds where each bird is improved by some neighborhood search methods.In MBO,after α birds are randomly generated in the initialization,β neighbor solutions around the leader are generated.If the best neighbor solution is superior to the leader,it replaces the leader.Then χ best unused neighbor solutions are shared with the first following bird at the following two lines.For each bird in the following lines,it is improved by the β-χ neighbor solutions and joins the χ shared solutions from the previous following bird.This sharing mechanism enhances the communication between the birds [29]. Finally,after the improvements for γ times,the current leader moves to the end of the formation and the first following bird in the left or right line becomes the new leader.

Currently,the MBO algorithm has shown superior performance in simple and U-shaped assembly line balancing problems [29,30]. Thus,this paper develops an EMBO to deal with the MALBP.The algorithm not only considers the features of MALBP,but also designs temperature acceptance and competitive mechanism to enhance its performance.The details of the proposed algorithm are described as follows.

3.1 Decoding with idle time reduction for MALBP

When assigning tasks to the multi-manned workstations in MALBP,the idle time including sequence-dependent idle time and remaining idle time will also occur.In Fig.1(b),the region marked grey presents the sequencedependent idle time and that marked green expresses remaining idle time.Since the reduction of the total idle time can improve the quality of solutions,we develop some task assignment rules embedded into the decoding mechanism to select operator processing tasks.

3.1.1 Task assignment rules for reducing the idle time Before assigning each task into the multi-manned workstations,four types of time and one candidate set should be determined first.

T_starti:the earliest start time of the current task i in the current workstation.If some predecessors of task i are assigned to current workstations,T_startiis equal to the maximum finishing time of these predecessors.Otherwise,T_startiis 0.

T_finishk:the finishing time of operator k before assigning task i.

T_beginik:the earliest start time of operator k in the current workstation when processing task i.It is equal to the maximum value of T_startiand T_finishk.

Idle_timek:the sequence-dependent idle time of the operator when processing task i.If T_startiis not more than T_finishk,Idle_timekis equal to 0;otherwise,Idle_timek=T_starti−T_finishk.

CA:Set of operators that can process the current task.If operator k processes task i and the finishing time of task i does not exceed the cycle time,which can also be expressed as T_beginik+tiCT,the operator k is added into CA.This set aims to check the cycle time constraint.

When assigning task i in each workstation,we first construct set CA.If CA is an empty set,another workstation is opened and continues to assign the current task.Otherwise,we select the operator with the smallest value of T_beginikfrom CA to process task i.Since the task can be processed at the earliest start time with this assignment rule,the remaining idle time can be reduced.If more than one operator is processing the current task at the earliest start time,the operator with the smallest value of Idle_timekwill be selected.This assignment rule aims to reduce the sequence-dependent idle time.

3.1.2 Decoding mechanism with the task assignment rules

To build a feasible balancing solution with less idle time,a new decoding mechanism combining the decoding proposed by Chen [27]and the above task assignment rules is proposed and described as follows.

Step 1Open a new workstation.

Step 2Assign the tasks.Firstly,it is assumed that there is one operator in the current workstation.The tasks from the feasible task assignment set are assigned to the current workstation with the above task assignment rules in turn until CA becomes an empty set.Then,the number of operators is gradually increased and tasks are reassigned to obtain different assignment plans of the current workstation.

Step 3Calculate the efficiency of different plans.An assignment efficiency is used to evaluate different assignment plans and is expressed as follows:(efficiency of each plan)=(the total processing time in current workstation)/[(number of operators) ×(cycle time)].

Step 4Select a plan with the minimum efficiency and update the feasible task assignment set.The assignment plan with the minimum efficiency is selected for the current workstation.The corresponding assigned tasks are removed from the feasible task assignment set.

Repeat the above steps until the feasible task assignment set is empty.

3.2 Initialization

In the proposed algorithm,each bird is encoded with the priority list of tasks.The length of this list is equal to the number of task n.The value of position i in this list represents the priority value of task i,and each priority value is randomly generated between 1 and n without repetition.For instance,one bird is constructed as [5,1,3,6,2,7,9,8,4],where the priority value of task 1 is 5 and that of task 2 is 1 and so on.This encoding provides the priority value of each task instead of the task assignments.Thus,this paper first determines the feasible task assignment set based on the above encoding,and then employs the above proposed decoding with idle time reduction to assign each task to a specific operator and workstation.The procedure to obtain a feasible task assignment set is as follows.

Step 1Set position x=1.

Step 2Construct the task candidate set.A task can be put into this set if:

(i) The task is unassigned;

(ii) Its predecessors have been put into the feasible task assignment set.

Step 3Put the task with the largest priority value from the candidate set in the xth position of the feasible task assignment set.

Step 4Remove the above task from the candidate set and x=x+1.

Repeat the above steps until all the tasks are assigned to the feasible task assignment set.

3.3 Neighborhood structure to improve the birds

Since EMBO is a neighborhood search meta-heuristic algorithm,the choice of neighborhood structures is crucial to generate a great quality solution [31].Thus,in the leader and following bird improvements,the proposed algorithm employs three neighbor search methods,including swap,insert and a new generation to optimize problems.All the methods are depicted as follows.

For the swap,two positions of the priority list are selected and the values of these positions are swapped.For the insert,a position is determined and the value of this position is inserted into another position.For the new generation,the priority list of tasks is regenerated randomly to replace the original list.

In the above neighbor structures,the swap and insert enhance the local search capability and the new generation can prevent the algorithm from falling into the local optimum.Thus,when a bird needs to be improved,one search method is randomly chosen to generate new neighbor solutions.

3.4 Acceptance criteria

In the original MBO,β neighbor solutions around each following bird will be generated by some neighbor search methods.Only when the best neighbor solution is superiorto the current bird,it replaces the current leader.This acceptance criterion may lose some great code snippets of the neighbors and make the algorithm get into a local optimization trap.Hence,a new acceptance criterion [30]based on the temperature in the SA algorithm is applied to our algorithm to avoid the above situation.In this criterion,if the best neighbor solution is not better than the current following bird,this neighbor is accepted with the probability of e−Λ/temp,where Λ=objective (neighbor)−objective (current solution) and

3.5 Competitive mechanism

After the algorithm improves the leader and the following birds for γ times,the first following bird in the left or right line will replace the current leader and hence has more opportunities to share its neighbors.However,this leader replacement is not fair for some birds emerging in the tail since these birds may have a great performance but have few opportunities to share their neighbors.Therefore,a competitive mechanism [32]is applied here to make up for this defect.After the leader replacement step,this mechanism is executed to adjust the position of the following birds.In each following line,all the birds are sorted in the descending order of the objective function.

4.Computational study

The presentation of the computational study consists of four parts:first,the proposed EMBO and the compared methods are calibrated by the design of experiments(DOE) technique coupled with the means of the multifactor analysis of variance (ANOVA) to ensure the comparison fairness;second,the original MBO and SA (the procedure of SA can refer to the research by Chen [27])embedded with different decodings are employed to evaluate the effectiveness of the proposed decoding;third,several EMBO variants are compared with each other to demonstrate the significance of the proposed improvements;finally,EMBO is compared with the state-of-theart methods with a target to tackle MALBP to test the performance of efficient EMBO.

To complete the above comparison experiments,372 benchmark problems proposed for Type-I simple assembly line balancing problems are applied to Type-I MALBPs.Among them,144 benchmark problems can be downloaded from the assembly line website:.The other 228 problems come from the research by Otto et al.[33]and contain 100 small-,100 middle-and 28 large-scale instances.The parameter umaxis set 3 according to [4].In the computational study,all the algorithms are encoded in C++programming language and are run on a computer with Intel(R) Core (TM) i5 CPU,2.80 GHz and 2.00 GB RAM.Besides,this paper employs the relative percentage deviation (RPD) to evaluate the results of all experiments.The calculation of RPD is

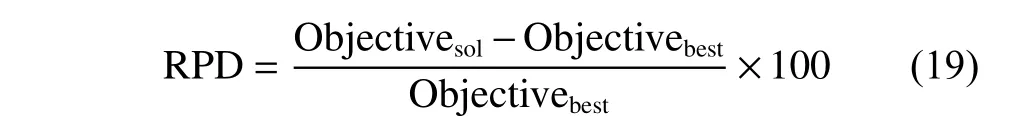
where Objectivesolis the objective function of the solution;and Objectivebestis the best objective function obtained by all algorithms.

4.1 Calibration of the proposed algorithm

Since the parameters have an awesome impact on the performance of EMBO,it has to calibrate its parameters and select the best parameter configuration.For the proposed algorithm,five parameters need to be calibrated and are called as the number of initial solutions α,the number of neighbor solutions to be considered β,the number of neighbor solutions to be shared χ,the number of tours γ and the initial temperature T.The levels of these parameters are listed as follows:

(i) The number of initial solutions α at eight levels:7,9,11,13,15,17,19 and 21.

(ii) The number of neighbor solutions to be considered β at four levels:5,6,7 and 8.

(iii) The number of neighbor solutions to be shared χ at six levels:2,3,4,5,6 and 7.

(iv) The number of tours γ at eight levels:50,100,150,200,250,300,350 and 400.

(v) The initial temperature T at six levels:0.4,0.5,0.6,0.7,0.8 and 0.9.

Through the full factorial design,there is a total of 8×4×6×8×6=9 216 parameter configurations. Each configuration is tested with 10 calibration instances whose task numbers are equal to 100.Note that these calibration instances come from the research by Otto et al.[33]and are different from the above 372 testing instances.Each configuration is solved 10 times to obtain 10 results.The stopping criteria for all the experiments are set as a CPU time limit of n × n ×ρ milliseconds where ρ=5.After 9 216×10×10=921 600 experiments,the DOE technique coupled with the means of the multifactor ANOVA is used to analyze all the results.The means plots of RPD with Tukey’s honest significant difference (HSD) 95% confidence intervals are used for the calibration of the proposed algorithm and shown in Fig.2.The analytic results from Fig.2 indicate that the best parameter combination is{α=13,β=7,χ=5,γ=350 and T=0.6}.Besides,we also use this method to verify the parameters of other compared algorithms,and the best parameter combinations are shown in Table 2 where HGA means the heuristics-mixed genetic algorithm.

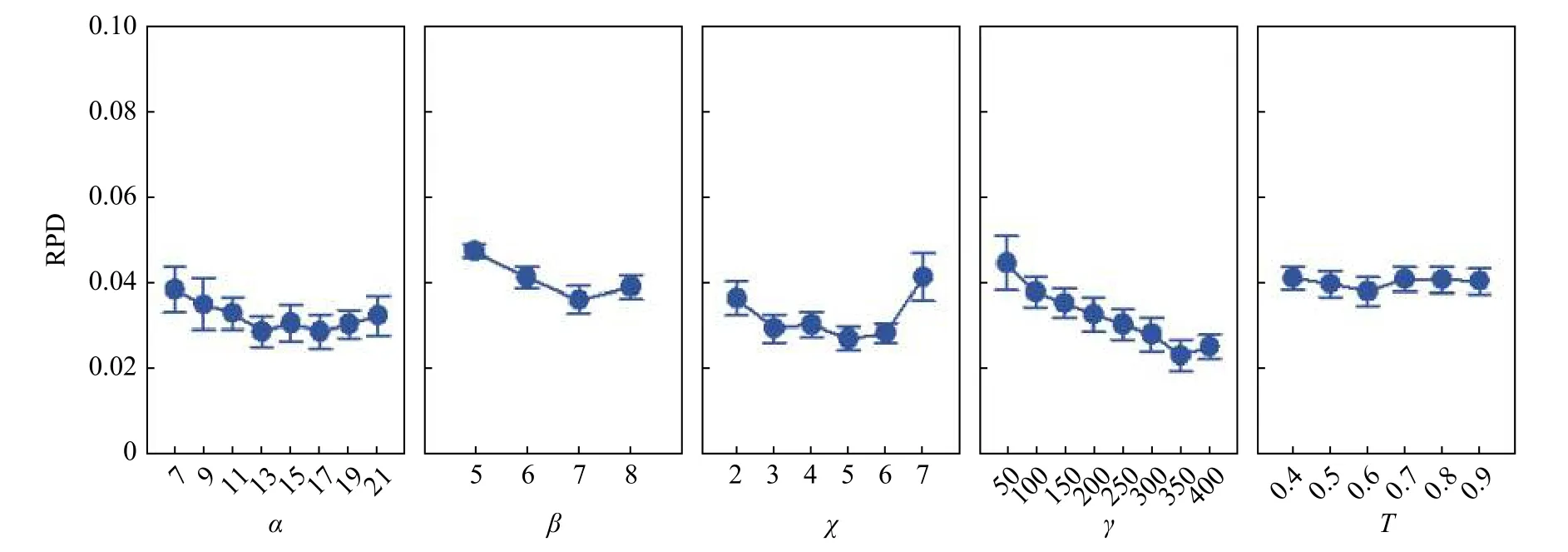
Fig.2 Means plots of RPD with Tukey’s HSD 95% confidence intervals for all the factors in the ANOVA calibration experiment for the proposed EMBO

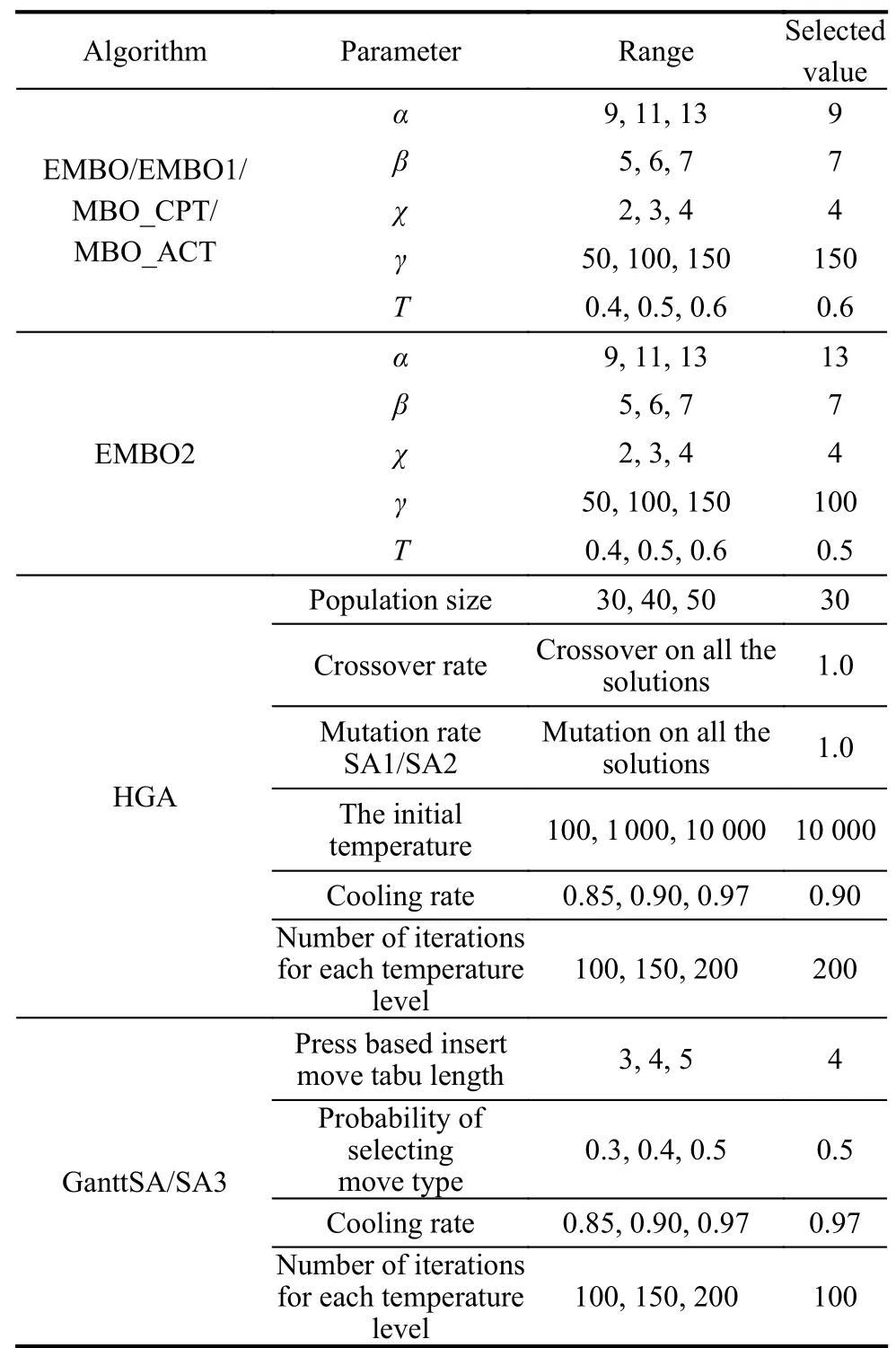
Table 2 Parameter values of all algorithms

4.2 Evaluation of the proposed decoding mechanism and improvements

For type-I MALBP,there are three existing decoding mechanisms.To test the effectiveness of the proposed decoding,this paper develops different versions of SA and EMBO by applying different decodings.Specifically,SA1 and EMBO1 use our proposed decoding with idle time reduction.SA2 and EMBO2 use the decoding proposed by[24]and [25].SA3 uses the decoding proposed by Kellegoz [26].All these algorithms are run on 372 benchmark instances with two stopping criteria n×n×10 and n×n×20,and each experiment is run for 10 times to obtain 10 results.Hence,a total of 18 600 experiment results are analyzed by the ANOVA technique and thus shown in Fig.3 and Fig.4.

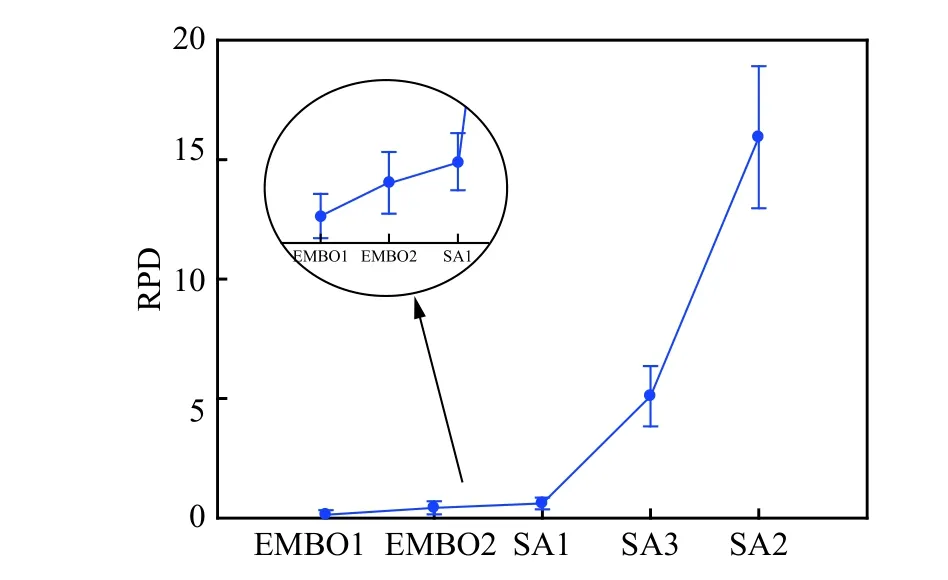
Fig.3 Means plot with Tukey’s HSD intervals at the 95% confidence level of the minimum solutions by different decoding schemes under n × n×10

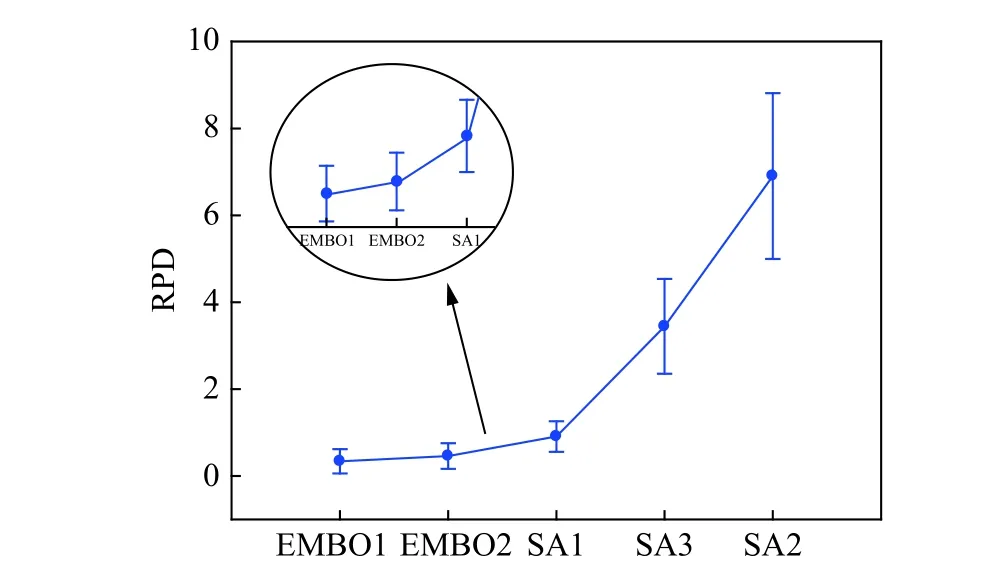
Fig.4 Means plot with Tukey’s HSD intervals at the 95% confidence level of the minimum solutions by different decoding schemes under n × n×20

In the two figures,it is clear that the SA1 is superior over SA2 and SA3 significantly and EMBO1 also outperforms EMBO2.These results suggest that the proposed decoding mechanism can reduce the remaining and sequence-dependent idle time effectively.In this comparison,we employ a population algorithm and a local search algorithm which are proved to have a great performance and have been widely used in assembly line balancing problems.Whether it is a population algorithm or a local search algorithm,our proposed decoding is very well embedded and performs the best.Besides,in terms of these two algorithms,no matter which decoding mechanism is embedded,the population algorithm EMBO outperforms the local search algorithm SA.Hence,this paper proposes EMBO to tackle MALBP.

Our proposed EMBO designs two improvements including acceptance criteria and competitive mechanism with a target to minimize the total number of workstations and operators.Hence,this section aims to evaluate the effectiveness of the two improvements and compares four MBO variants including original MBO considering nothing,MBO_ACT just considering acceptance criteria,MBO_CPT just considering competitive mechanism and EMBO considering all improvements.All these MBO variants are run on 372 benchmark instances with the stopping criteria n×n×20,and each experiment is run for 10 times to obtain 10 results.Hence,a total of 14 880 experiment results are analyzed by the ANOVA technique and shown in Fig.5.

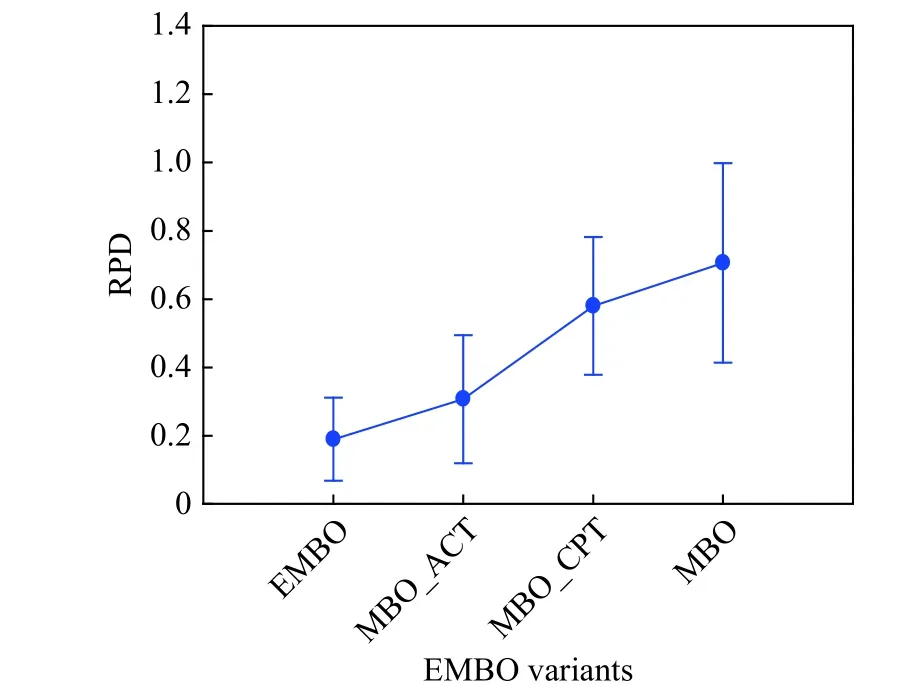
Fig.5 Means plots with Tukey’s HSD intervals at the 95% confidence level of the minimum solutions by all MBO variants under n × n×20

In Fig.5,it can be observed that the average RPD values of all instances obtained by the variants MBO_ACT and MBO_CPT are both smaller than those obtained by the original MBO.This means that in MALBP the two proposed improvements embedded into MBO can effectively improve the performance.Meanwhile,the proposed EMBO considering both improvements performs better than MBO_ACT and MBO_CPT,which indicates that the combination of two improvements is more effective than the separate improvement.

Hence from the two above comparison experiments,the effectiveness of proposed decoding and improvements is positive.

4.3 Comparison with the state-of-the-art methods

To test the performance of the proposed EMBO algorithm,this paper further compares the proposed EMBO with four state-of-the-art algorithms.The compared algorithms are HGA [34],SA1 [27],SA2 [25]and Gantt-SA [26].All these algorithms have been successfully applied to solve Type-I MALBP.Two stopping criteria with n × n ×ρ where p=10 and p=20 are set for the comparison experiments.Each algorithm is also run on 372 instances for 10 times and the minimum and average results are presented in Tables 3−5 for comparison.

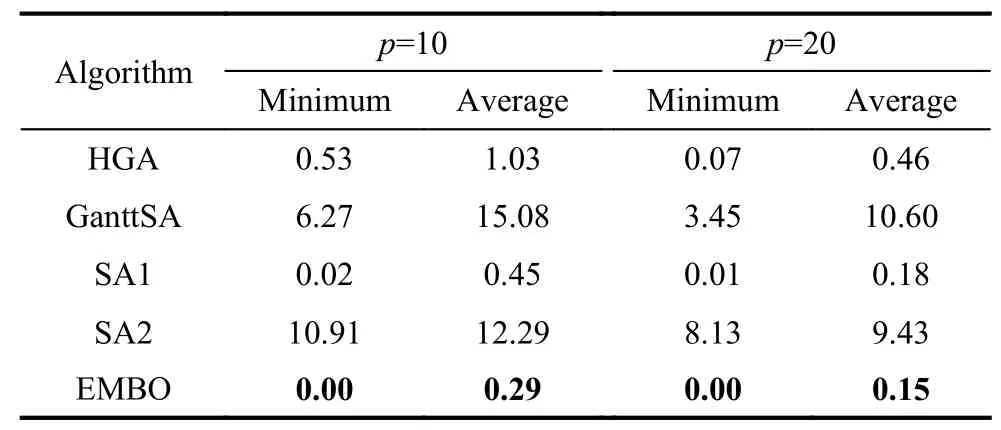
Table 3 Comparison results for small-scale instances

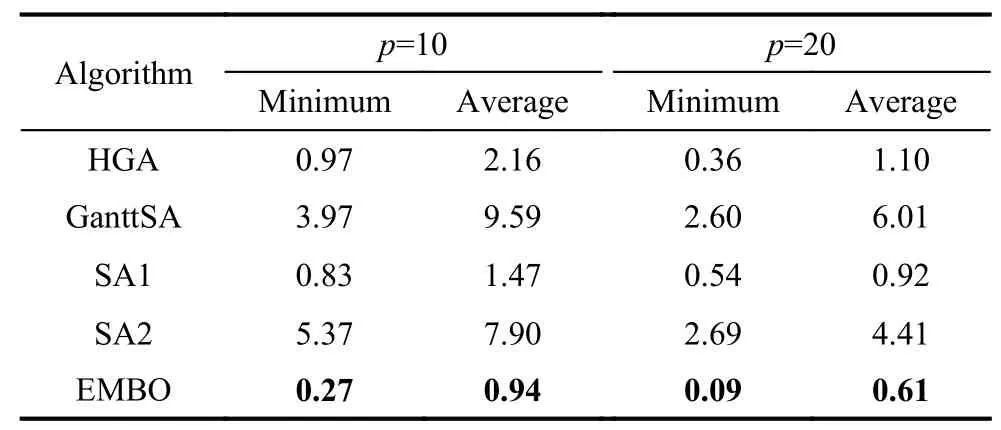
Table 4 Comparison results for middle-scale instances

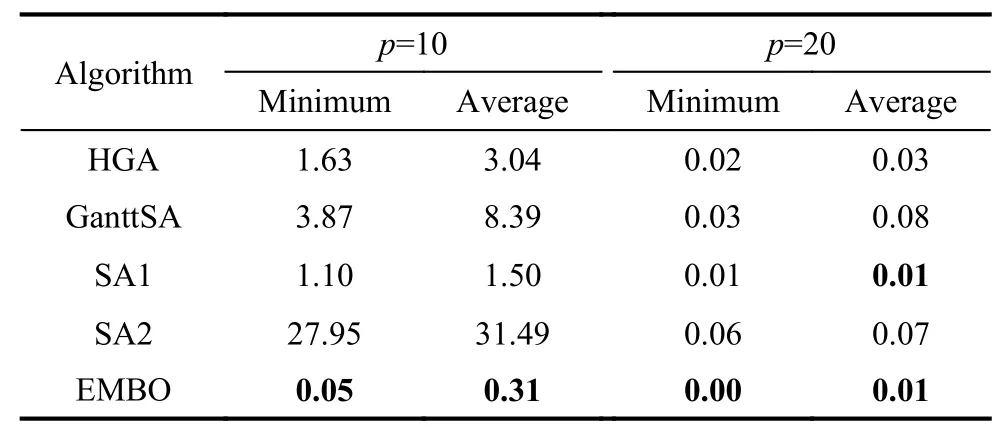
Table 5 Comparison results for large-scale instances

Table 3 reports the comparison results for small-scale instances including Merten7,Bowman8,Jaeschke9,Jackson11,Mansoor11,Mitchell21,Roszieg25,Heskia28,Buxey29 and 100 small-scale instances proposed in [30].For the small-scale instances,the proposed EMBO performs the best compared with the four state-of-the-art methods.Specifically,EMBO is ranked first,followed by SA1,HGA in turn;while GanttSA and SA2 are the worst performers.Although the performances of the four stateof-the-art methods are a little bit worse,SA1 and HGA can also obtain the best results as well as EMBO for most instances,and GanttSA and SA2 obtain the same results as EMBO for several instances.

Table 4 reports the comparison results for middle-scale instances including Sawyer30,Lutz32,Gunther35,Kilbridge45,Hahn53,Warnecke58 and 100 middle-scale instances proposed in [30].For middle-scale instances under the stop criterion n×n×10,the average minimum values of RPD by HGA,GanttSA,SA1,SA2 and EMBO are 0.97,3.97,0.83,5.37 and 0.27 respectively.The proposed EMBO also has the best performance while the SA2 obtains the worst results.If the RPD is used to rank algorithms,apart from EMBO,SA1 ranks the first and HGA follows with GanttSA and SA2 being the worst two.For the stop criterion n×n×20,it has the same conclusion that EMBO performs the best.

Table 5 reports the comparison results for large-scale instances including Tonge70,Weemag75,Arcus83,Lutz89,Mukherje94,Arcus111,Barthol148,Scholl297 and 28 large-scale instances proposed in [30].For largescale instances under two stop criteria n×n×10 and n×n×20,it is clear that the proposed EMBO is superior over the other four compared algorithm.As the scale of instance is extended,it turns more and more difficult for SA1 and HGA to obtain the best results as EMBO.If the RPD is used to rank algorithms,it has the same ranks as that of the middle-scale instances.In summary,we can conclude that our proposed algorithm is more effective in solving the Type-I multi-manned assembly line balancing problem.

Furthermore,we further apply the ANOVA method to analyze the performance of the proposed algorithm.The means plots with Tukey’s HSD intervals at the 95% confidence level of the minimum and average solutions by different algorithms under n×n×10 and n×n×20 are depicted in Fig.6 and Fig.7.For the space limitation,this paper just presents the plots of the minimum solutions.In the presented figures,the algorithms are sorted in an ascending order of RPD.It is observed that EMBO is still ranked the first,followed by SA1 and HGA;while Gantt-SA and SA2 are the worst performers.Hence,we can conclude again that the proposed EMBO outperforms the compared algorithm from a statistical viewpoint.

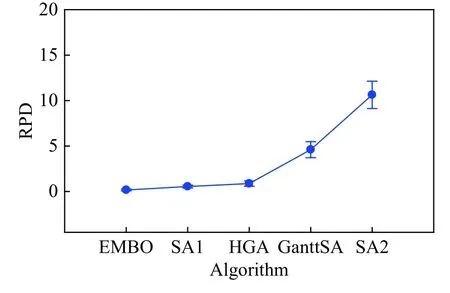
Fig.6 Means plots with Tukey’s HSD intervals at the 95% confidence level of the minimum solutions by different algorithms under n× n×10

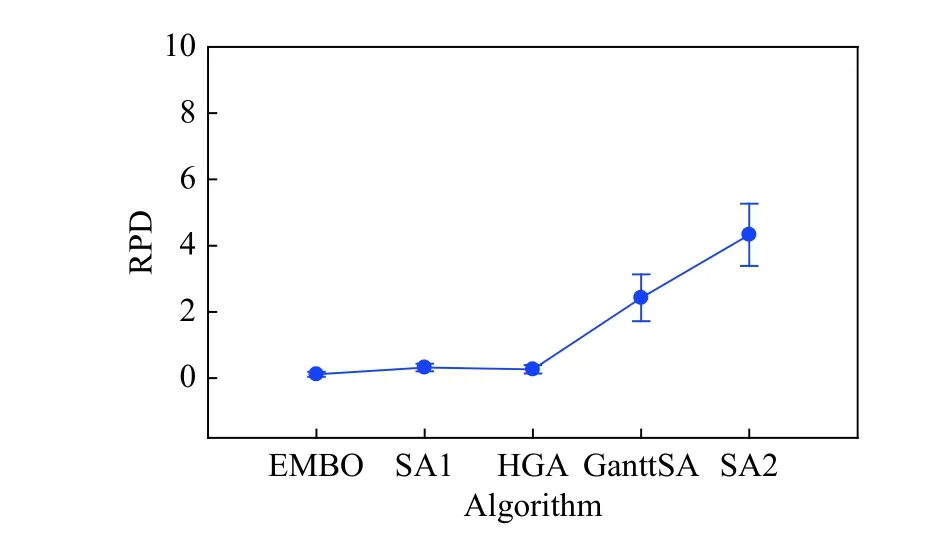
Fig.7 Means plots with Tukey’s HSD intervals at the 95% confidence level of the minimum solutions by different algorithms under n× n×20

In summary,due to the characteristics of MALBP,the proposed algorithm designs a decoding mechanism with idle time reduction and two improvements including acceptance criteria and a competitive mechanism to minimize the total number of workstations and operators.Correspondingly,the computational study carries out three types of comparison experiments to obtain three main conclusions:

(i) The proposed decoding mechanism is more effective in terms of reducing the idle time compared with the existing decoding methods.It can also be very well embedded into the population and local search algorithms.

(ii) The proposed two improvements are proved to be successful in improving the performance of the original MBO.The improvement effect of the combination is more significant.

(iii) The proposed EMBO outperforms the state-of-theart methods in all small-,middle-and large-scale MALBP instances.

5.Conclusion and future work

Due to the complexity of the assembly tasks of products such as the engine,the central assembly plants usually employ many operators instead of robots to complete the production.Hence,this paper addresses the MALBP tominimize the total number of workstations and operators.Following the problem description,EMBO is developed for problem settlement.In this algorithm,task assignment rules are applied to the decoding mechanism to reduce the sequence-dependent and remaining idle time.Three neighbor structures are blended to improve the leader and the following birds.Besides,new acceptance criteria and a competitive mechanism are employed to enhance the performance of EMBO.Finally,three comparison experiments are designed to analyze the performance of the proposed decoding mechanism and improvements of EMBO.In the experiments,two existing decoding mechanisms,four MBO variants and four algorithms are involved.The computational results indicate the effectiveness of the proposed decoding and two improvements.The proposed EMBO outperforms the four compared algorithms.

The developed decoding mechanism and EMBO can assist production managers to adjust or design the multimanned assembly line layouts to further reduce the line length and operator costs.Nevertheless,the lack of more realistic constraints and multi-objective optimization makes it difficult to solve a practical problem.Hence,based on this work,future research will consider the resource constraints in MALBP.Additionally,future research can also consider that some robots may replace part operators in multi-manned workstations and further achieve the optimization of this new problem.