An improved multi-objective optimization algorithm for solving flexible job shop scheduling problem with variable batches

WU Xiuli ,PENG Junjian ,XIE Zirun ,ZHAO Ning ,and WU Shaomin

1.School of Mechanic Engineering,University of Science and Technology Beijing,Beijing 100083,China;2.Kent Business School,University of Kent,Kent CT2 7FS,UK

Abstract:In order to solve the flexible job shop scheduling problem with variable batches,we propose an improved multiobjective optimization algorithm,which combines the idea of inverse scheduling.First,a flexible job shop problem with the variable batches scheduling model is formulated.Second,we propose a batch optimization algorithm with inverse scheduling in which the batch size is adjusted by the dynamic feedback batch adjusting method.Moreover,in order to increase the diversity of the population,two methods are developed.One is the threshold to control the neighborhood updating,and the other is the dynamic clustering algorithm to update the population.Finally,a group of experiments are carried out.The results show that the improved multi-objective optimization algorithm can ensure the diversity of Pareto solutions effectively,and has effective performance in solving the flexible job shop scheduling problem with variable batches.

Keywords:flexible job shop,variable batch,inverse scheduling,multi-objective evolutionary algorithm based on decomposition,a batch optimization algorithm with inverse scheduling.

1.Introduction

Optimization of batch scheduling is one of the important research topics in batch scheduling [1].This paper aims to investigate the flexible job shop scheduling problem with variable batches (FJSP-VB).Compared to the classic flexible job shop scheduling problem [2],the FJSP-VB needs to determine the batch size for each job besides machine assignment and machine scheduling.The FJSP-VB is therefore more complex than the FJSP and it is challenging to solve it.

According to different job shop types,batch scheduling can be categorized into the parallel machine batch scheduling problem [3,4],the flow shop batch scheduling problem [5−8],the job shop batch scheduling problem [9],and the flexible job shop batch scheduling problem [10−17].Since Reiter [18]first introduced the concept of“batch flow”in the context of the job shop scheduling problem in 1966,the scheduling problem considering batch production has attracted increasing interest from authors.However,there are some challenges on batch scheduling problems in the FJSP context that needs investigation [10].

There are some studies on the FJSP that considers batches.For example,Zhang et al.[1]proposed a competitive cooperative bird migration optimization algorithm for the FJSP-VB.They designed a chromosome with a three-dimensional (3D) structure to optimize the batch size.For the same problem,Novas [10]used the constraint programming and defined the maximum batch number of jobs in the constrained programming (CP)model,according to which they further generated the solution space.Although the batch size can be set to zero so that the batch size can be reduced,there are still a large solution space and challenges for the optimization algorithm.Defersha et al.[13]used the genetic algorithm to study the FJSP,considering batches.Although the variable batch problem was considered,the batch number was assumed known.This may limit the overall optimization of the problem.Ham et al.[14]proposed the CP model and the mixed integer programming (MIP) model with efficient inequality to solve the FJSP with parallel batch processors.Zhou et al.[15]studied the multi-objective FJSP with batch and dynamic factors in the aeroengine blade manufacturing factory.They improved the hyper-heuristics with multi-agent.Bozek et al.[16]used the tabu search to solve the FJSP-VB.Jia et al.[17]designed a multi-objective ant colony optimization algorithm to solve the FJSP with batches.They proposed a local optimization method to improve the ant colony op-timization algorithm.

Existing literature usually assumes that the batch size of each job is known in advance,under which the optimization result is simply a scheduling solution of the known batches.It is hard to obtain the globally optimal solution for the FJSP-VB.Therefore,this paper proposes an improved multi-objective optimization algorithm (IMOA).The main contributions of this work are as follows.

(i) A model of the FJSP-VB to optimize the makespan and the transportation time is formulated.

(ii) An IMOA is proposed to search the global optimal solution for the FJSP-VB.

(iii) A batch optimization algorithm based on inverse scheduling (BOA-IS) is proposed to optimize the batch size.

(iv) Two strategies for updating the neighborhood are proposed to increase the diversity of the population.

The remainder of the paper is organized as follows.Section 2 describes the FJSP-VB.Section 3 proposes the IMOA.Section 4 provides numerical experiments.Section 5 concludes the paper and proposes future work.

2.FJSP-VB

2.1 Problem description

The FJSP-VB can be described as follows.There are n jobs to be processed on m machines.Each job is composed of a number of operations and each operation is performed on available machines.The processing time of an operation on its available machines may be different.The demand amount of each job can be divided into multiple sub-batches to process.Operations belonging to the same sub-batch of a job should follow the processing constraints.Operations in different sub-batches of the same job need not be subject to the constraints.Some time is required for jobs to transfer from one machine to another.The task of the FJSP-VB is to assign the available machines for each operation in each sub-batch and then determine the processing sequence on each machine.The objective is to optimize the makespan and the transferring time.

In order to simplify the problem,some assumptions are made as follows.

(i) The initial available time of all machines is 0,and all jobs can be processed at t=0;

(ii) The amount of the demand of each job is known in advance;

(iii) Each sub-batch is independent during scheduling;

(iv) The processing time of the operation on different available machines is known;

(v) Machine maintenance,emergency orders or machine breakdown is not considered in this study.

2.2 Model formulation

2.2.1 Notations

Some notations are given in Table 1.

Table 1 The notations

2.2.2 Formulation of FJSP-VB

The following mathematical model can then be given.

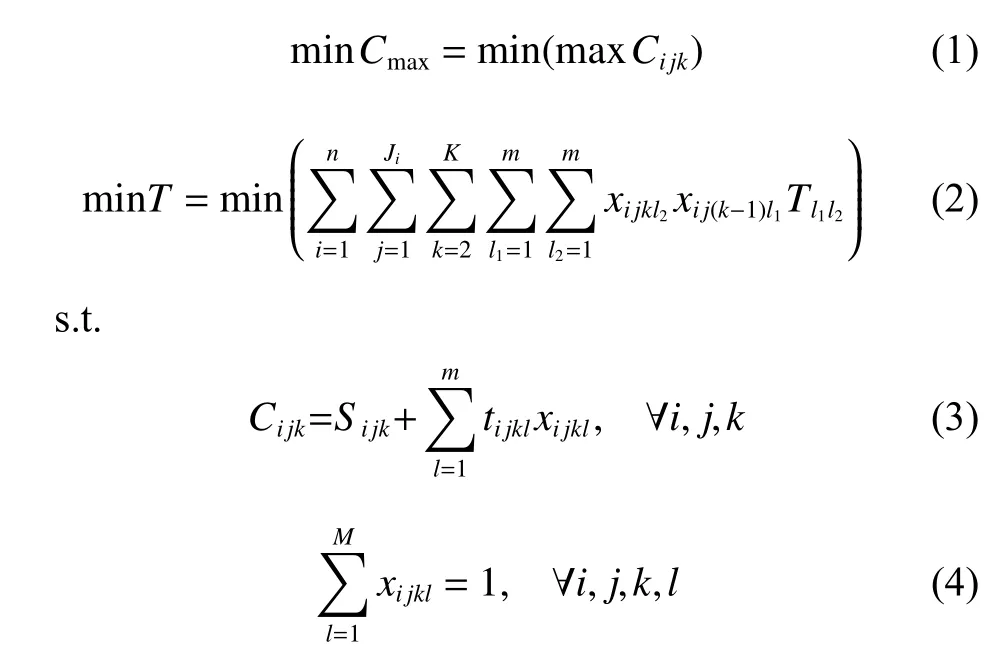
Equations (1) and (2) are objective functions.Equation (3) indicates that the completion time of each operation equals the sum of the start time and processing time.Equation (4) indicates that each operation can only be processed on one machine.Equation (5) indicates that the start time of an operation is greater than the sum of the completion time of its previous operation and the transferring time.Equation (6) indicates that the sum of the sub-batches for one job is equal to the demand amount.Equation (7) indicates that the overlap between operations is not allowed.Equation (8) indicates that the start processing time of all job batches can start from zero.Equation (9) indicates that the size of each sub-batch of one job is not greater than its demand amount.Equation(10) indicates that the number of sub-batches of one job is not greater than its demand amount.Equations (11)−(13)define the value range of the variable,respectively.

3.IMOA

3.1 IMOA flowchart

In the existing literature,little application of the multi-objective evolutionary algorithm based on decomposition(MOEA/D) algorithm in the flexible job shop batch scheduling problem can be found [19].MOEA/D has some drawbacks in solving the multi-objective optimization problem.When the Pareto front has a heavy tail,the performance of the MOEA/D algorithm is greatly influenced.Hence,some improved versions of the MOEA/D have been proposed.For example,Dong et al.[20]proposed a chain segmentation based strategy.The approximate Pareto front shape is derived from the initial population,the shape of the front is cut equally to generate the weight vector,and the distribution performance of the algorithm is improved according to the improved weight vector.Jiang et al.[21]proposed a hybrid multi-objective evolutionary algorithm based on decomposition and solved the Pareto front problem with the hybrid algorithm.In order to solve the homogenization problem of neighbors,some MOEA/D based improved algorithms have been proposed [22,23].

In order to avoid being trapped into local optimums during searching and to improve the poor performance of MOEA/D in solving multi-objective combinatorial optimization problems,we propose two methods as follows:

(i) When updating the neighborhood,a threshold is set to limit the updating individuals.For example,there are 10 neighbors and eight neighbors that can be considered to replace the original individuals.If the threshold is 0.5,only four neighbors can be used to update the population.Thus,the diversity of the population is ensured by avoiding generating too many similar or same individuals.

(ii) A clustering algorithm is employed to dynamically adjust the diversity of the neighbors.When the number of individuals in the same cluster exceeds the threshold,some individuals in other clusters are used to replace some of the individuals to avoid premature.

The pseudocode of the IMOA is shown below.

Step 1Initialize parameters,including population size popsize,crossover probability pc,mutation probability pm,neighborhood weight vector number T,maximum iteration number Max_iterate;initialize the population Pop and the external population EP;initialize the weight vector w and ideal point z.

Step 2Assign a weight vector to each sub-problem and set the iteration number iter=0.

Step 3For each individual p in the population,randomly select two individuals in its neighborhood.A random number between 0 and 1 is generated.If pc is larger than the random number,the two individuals are crossed to generate an offspring;otherwise,the crossover operation step will be skipped.

Step 4Randomly generate a random number between 0 and 1.If pm is larger than the random number,the two selected individuals will be mutated to generate two offspring individuals;otherwise,the mutation operation step will be skipped.

Step 5Execute the BOA-IS algorithm to adjust the batch size of sub-batch of each job.

Step 6Update the ideal solution z.

Step 7Update the neighborhood solution with the threshold strategy.The neighborhood individuals are randomly updated according to the similarity with a predefined ratio.

Step 8Update the external population EP.Compare the offspring individuals with the individuals in the external population,and remove the individuals dominated by the offspring individuals in the external population.If the offspring individuals are not dominated by any of the individuals in the external population,they are added to the external population.

Step 9Adjust the diversity of neighborhood individuals dynamically with the clustering algorithm.The neighborhood individuals of the current individual x are selected for the cluster analysis.If the number of the individuals with a very high similarity in one cluster exceeds a predefined threshold,update those individuals partially.

Step 10If the terminal condition is met,check whether the batch number of a job is greater than 1 or not.If so,execute Step 11.Otherwise,return to Step 3.If the terminal condition is not met,return to Step 3 directly.

Step 11Compare the solution with the solution of the previous iteration.If the solution in this iteration is better,increase the batch number of jobs on the critical path of the non-dominated solution,and initialize the batch information,and return to Step 3.Otherwise,output the solution of the previous iteration and then end the searching.

3.2 Details of the IMOA

3.2.1 Coding

To propose an evolutionary algorithm,the first task is to represent the problem into a chromosome.An effective chromosome should include not only the scheduling information,but also the batching information of each job.We therefore propose an encoding method for the FJSPVB.A chromosome is composed of three parts.The first part is the batch number for each job,the second part is the size for each batch size,and the last part is the scheduling information.For example,if there is an instance which has three jobs,each job has three operations,and the demand amount of each job is 10.The chromosome is encoded,as shown in Fig.1.There are three genes (i.e.,“2 1 1”) in the first part,which means that job 1 is divided into two sub-batches,and job 2 and job 3 are both one sub-batch respectively.There are four genes (i.e.,“4 6 10 10”) in the second part,which indicates that the numbers of the two sub-batches of job 1 are 4 and 6 respectively,the size of the sub-batch of job 2 and job 3 is 10.In the third part of batch scheduling information,taking the second occurrence of“2-1”as an example,it represents the second operation of the first sub-batch of job 2.

Fig.1 An example for encoding

3.2.2 BOA-IS for decoding

Reverse scheduling is a scheduling optimization method by adjusting parameters to further optimize the original feasible scheduling solution.Up to now,the study on reverse scheduling is still in its early stage [24].In this study,we introduce the idea of reverse scheduling in designing the scheduling algorithm.Since the processingparameters such as processing time,production batch size of job,and transferring time between machines,of the FJSP-VB are not allowed to be changed,the only parameter for the inverse scheduling method to adjust is the sub-batch size of each job,which is also a decision variable.During adjusting,it is necessary to ensure that the amount of the demand of each job cannot change.Therefore,when the batch bijof a certain sub-batch j of job i is increased by nij,the batch size of other sub-batches of the job should be reduced accordingly.To calculate the size of each sub-batch of job i,a virtual variableindicating the quantity of the sub-batch that the current subbatch has increased or decreased is introduced based on the calculation of nij.That is,means that the subbatch size of bijis increased,andmeans that the sub-batch size of bijis decreased.Thus the total batch size of job i becomesIn order to keep the original batch size unchanged,we need to scale down the subbatch size.The sub-batch size isreduction.Thus the batch size of the sub-batch j of job i is exactly equal to bij+nij.It can be expressed as

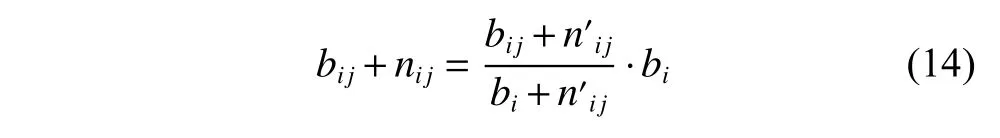
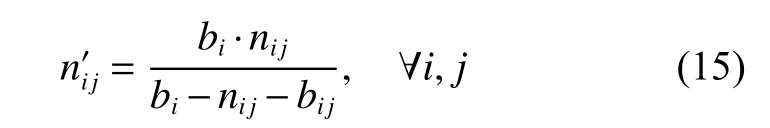
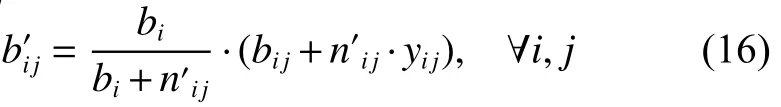
BOA-IS makes full use of the idle time slot of the scheduling solution,obtained by the gap extrusion method(GEM) [25].It adjusts the batch size of each sub-batch with the aims to reduce the idle time slot,improve the utilization of machines,and reduce the makespan.The detailed steps are as follows.The first step is to find all the idle time slots available on the machine for the current operation to be scheduled.The second step is to find the idle time slots whose starting time are greater than the completion time of the precedence operation and the slot length is greater than its processing time.

To make it easier to understand the BOA-IS,we give an example in Table 2,where M1,M2and M3indicate machine 1,machine 2 and machine 3,respectively.

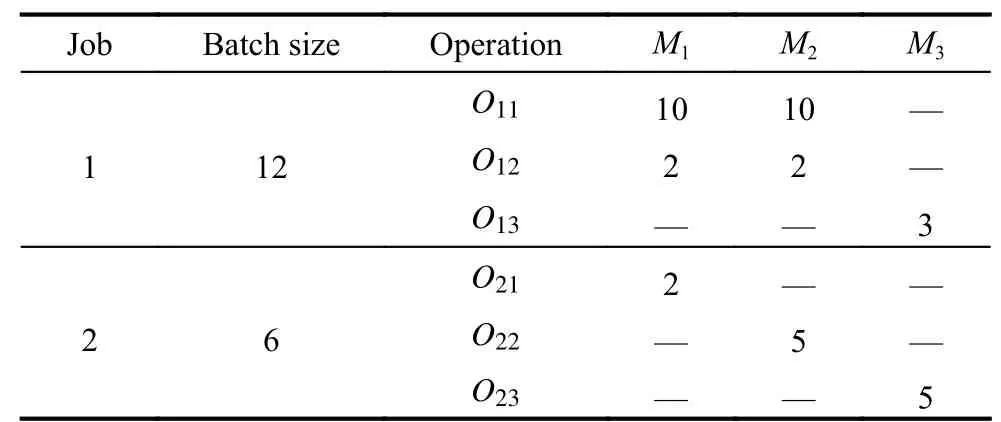
Table 2 An example for FJSP-VB

During the processing process,job 1 is divided into two sub-batches to process and job 2 is only one batch to process.The batch scheduling information in a chromosome is [O111,O121,O211,O112,O113,O212,O213,O122,O123].The scheduling Gantt chart is shown in Fig.2.Each rectangle represents an operation.The data in each rectangle is in the form of“a/b/c”,where a represents the job index,b indicates the sub-batch index and c means the operation index.For example,“1/2/2”means the operation 2 in sub-batch 2 of job 1.

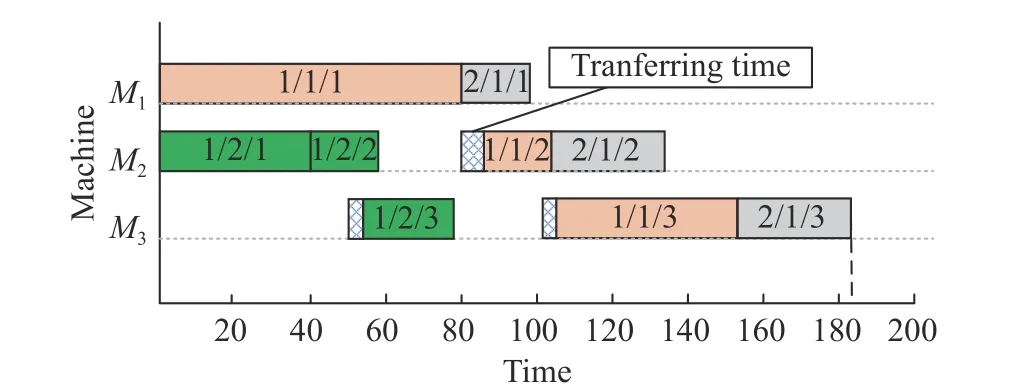
Fig.2 Scheduling solution

It can be seen from Fig.2,the length of the idle time slot on machine 2 is 32.The processing time of the first operation of job 1 on machine 2 is 10 and the second operation of job 1 on machine 2 is 2.If we add the batch size by 1 for the second sub-batch of job 1,the idle time slot length is reduced by 10+2.Hence,for this idle time slot,we adjust the sub-batch size by b.The following constraint should therefore be met.

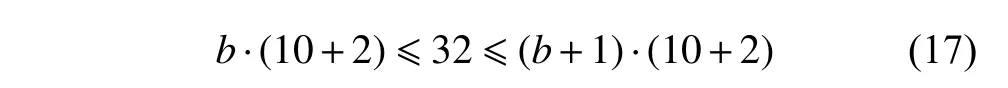
According to (17),the batch size of the second subbatch of job 1 can be accurately increased by 2.Since the total demand amount is a constant,the batch size of the first sub-batch of job 1 has to be reduced by 2 accordingly.Thus,the adjusted scheduling solution is shown in Fig.3.Comparing Fig.2 with Fig.3,one can see that themakespan is reduced from more than 180 time units to fewer than 180 time units.Hence,it can be concluded that the BOA-IS is effective in reducing the makespan of a scheduling solution.

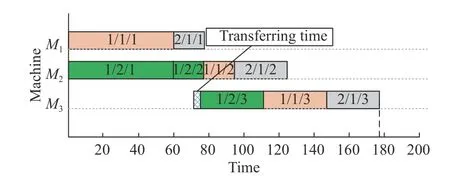
Fig.3 Adjusted scheduling solution

To be more general,the pseudo of the BOA-IS is given belows.Each step of the BOA-IS is as follows.

Step 1Input a chromosome and select the batch scheduling information of the chromosome,where Mljrepresents the jth operation of machine l and the total number of Mljis defined as len(Ml.);S(Mlj) indicates the start time of the jth operation of machine l;E(Mlj) indicates the completion time of the jth operation of machine m;bMljis the batch size of Mlj.

Step 2Call the gap extrusion method to generate a scheduling solution and record the result before adjustment.

Step 3Traverse each of the machines.

(i) Traverse the operations on the current machine in turn.

(ii) Judge whether Mljis the first operation processed on the current machine.If not,go to Step 6;otherwise judge whether the start time of Mljis larger than zero,the batch size of Mljis larger than 1,and the demand amount of the corresponding job is larger than 1.If yes,reduce the batch size of the current sub-batch and adjust the batch sizes of the other sub-batch of the job;otherwise,return to (i).

(iii) Check whether the start time of Mljis greater than the completion time of its precedence operation and the batch number of the current job is larger than 1,and Mljand Ml(j−1)are not in the same sub-batch.If yes,increase the batch size of Ml(j−1),and reduce the batch size of the other sub-batches of the corresponding job.

Step 4Check whether each machine has been traversed.If not,return to Step 3;otherwise,check whether the adjusted solution dominates the original one.If yes,update the original solution with the adjusted solution and return to Step 3 to continue traversing machines;otherwise,output the solution before adjustment.

The detailed steps of batch adjustment of jobs in the pseudo of the BOA-IS corresponding to Ml(j−1)are as follows.

Step 1Calculate the idle time slot length T1of the current machine.

Step 2Find all the operations that are located before Mljand belong to the same sub-batch as Mljon machine l and store them into record set O.

Step 3Sum the processing time of the operation in set O and record it as T2.

Step 4Calculate the increment or decrement of batch size bMljcorresponding to Mljaccording to the constraint(16).

Step 5If the batch size after adjustment is larger than the demand amount of the job or less than zero,readjust it;otherwise,accept this adjustment.

Since the chromosome encoding method does not include the machine assignment,it is necessary to decode the chromosome according to GEM proposed by Wu et al.[25].The detailed steps of GEM are as follows.

Step 1Input a chromosome.

Step 2Divide the chromosome into three parts,i.e.,the batch number of each job,the batch size of each subbatch and the batch scheduling information.Then calculate the processing time of each sub-batch according to the batch size.

Step 3In the batch scheduling part,denoted as X,select an operation Oijkin X.

(i) Select all the available machines M for operation Oijk.

(ii) Search each of the idle time slots on each machine from the completion time of operation Oij(k−1)(i.e.,the starting point) to the current completion time on the current machine (i.e,the end point).Compare the processing time of the operation and the idle time slot length.If the length is greater than the processing time of the operation,record the idle time slot and append it in the record set Q.

(iii) Check whether each of the idle time slots on all the available machines has been traversed.If yes,choose the idle time slot whose start time is the earliest in record set Q to insert the operation Oijk.Otherwise,return to (ii).

(iv) Judge if all operations have been traversed.If yes,the GEM ends;otherwise,return to Step 3.

3.2.3 Clustering algorithm

By setting a threshold,the updating part of the neighbors can avoid the rapid homogenization of the neighborhood individuals,but the neighborhood individuals will gradually lose diversity with iterations.In order to improve the diversity of the population,IMOA introduces the clustering algorithm to dynamically adjust the diversity of neighborhood individuals.Fig.4 is its flow chart.

The detailed steps are as follows:

Step 1Generate the neighborhood of the chromosome;

Step 2Select an individual x that is not clustered into a cluster.

Step 3Calculate the similarity between individual x and the other individual in the neighborhood,and add individual x to the cluster that includes the individual with the highest similarity with individual x.Judge if all the individuals have been added to one of the clusters.If yes,go to Step 4.Otherwise,return to Step 2.The method to calculate the similarity between two chromosomes is shown in Fig.5.If the alleles of two chromosomes are the same,the score will be 1;0,otherwise.For the example in Fig.5,the total score is 8.Hence the similarity of the two chromosomes is 8.

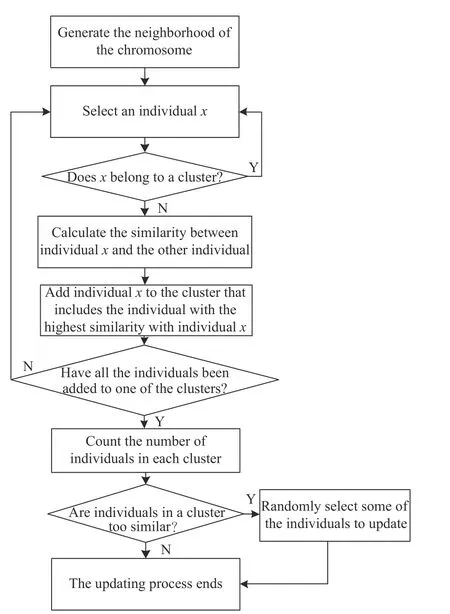
Fig.4 Flowchart of the clustering algorithm

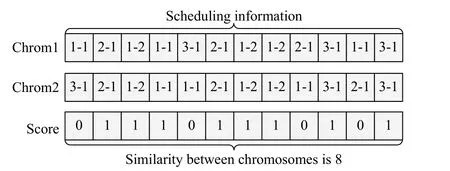
Fig.5 An example to show how to calculate the similarity

Step 4Count the number of individuals in each cluster.If the number of individuals in a certain cluster is larger than half of the number of individuals in the neighborhood,randomly select some of the individuals to update.Two updating strategies are randomly selected totake into account the distribution expansion and the distribution uniformity of Pareto solutions.The two methods are as follows.If the number of individuals in all clusters is smaller than half of the number of individuals in the neighborhood,go to Step 5.

(i) Initialize the individual directly.

(ii) Select the individual of the external cluster which are inclined to the peak or the long tail.First cross it with the individual to be updated to obtain an offspring and then mutate the offspring.

Step 5The algorithm ends and the updating is completed.

3.2.4 Crossover

In IMOA,in order to avoid the disadvantage of the single crossover method and explore the solution space better,we employ two crossover methods and they are randomly chosen to generate new individuals,including linear order crossover (LOX) and multi-point crossover (MPX).

(i) LOX operation (see Fig.6).Randomly select two positions in the batch scheduling information part of the chromosome.Exchange the genes between two positions of the parents to generate the offspring.

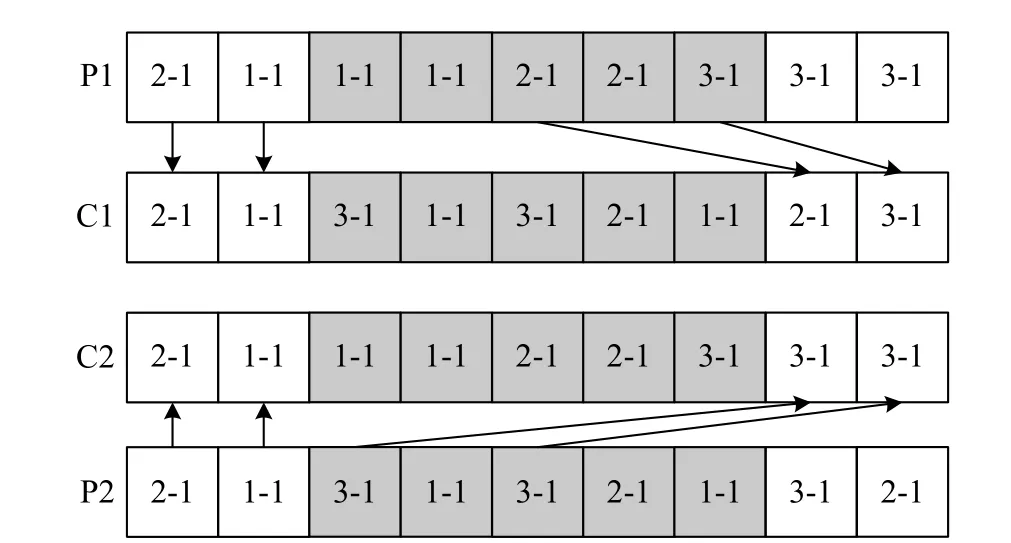
Fig.6 An example to show how the LOX works

(ii) MPX operation (see Fig.7).Randomly select two positions in the batch scheduling information part of the chromosome,and exchange the genes in the corresponding positions in the parents and inset the rest genes to the other positions in order.

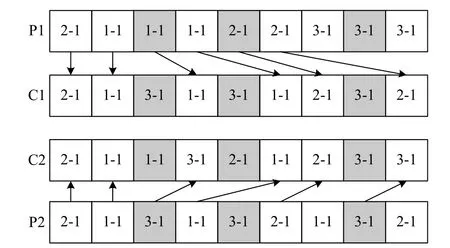
Fig.7 An example to show how the MPX works

3.2.5 Mutation

Three mutation methods are randomly employed to further explore the solution space and improve the local search ability of the algorithm.They are the reverse based mutation,the exchange based mutation and the insertion based mutation.

(i) The reverse based mutation (see Fig.8) is to randomly select two positions,reverse the genes within the two positions,and then fill the corresponding position of the chromosome to generate a new chromosome.

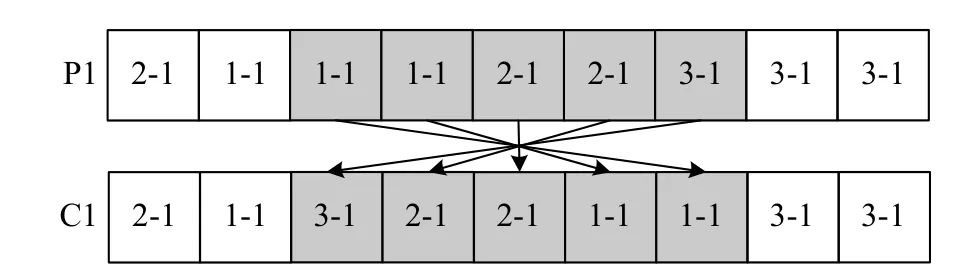
Fig.8 An example to show how the reverse based mutation works

(ii) The exchange based mutation (see Fig.9) is to select two positions randomly in the batch scheduling information part,and exchange the genes at these two positions to generate a new chromosome.

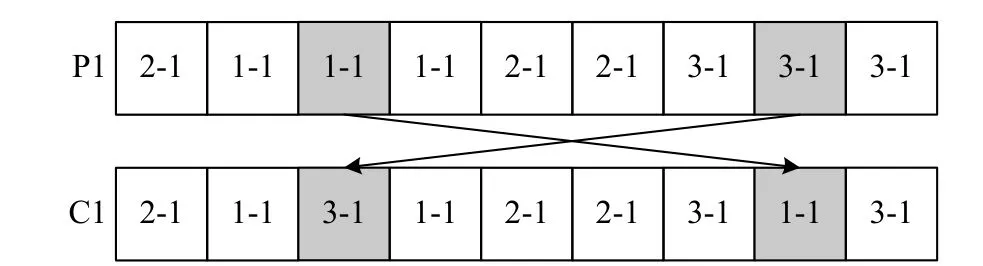
Fig.9 An example to show how the exchange based mutation works

(iii) The insertion based mutation (see Fig.10) is to first select two positions randomly in the batch scheduling information gene segment,and then insert the gene in one selected position into another selected position to generate a new chromosome.

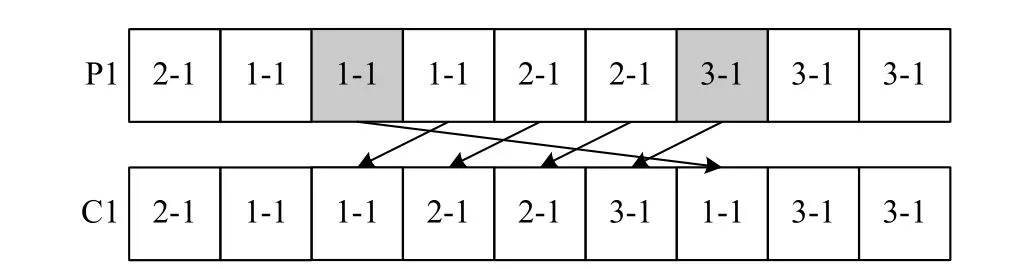
Fig.10 An example to show how the insertion based mutation works

3.3 Computational complexity of the IMOA

To analyze the performance of the proposed IMOA,we need to compute its computational complexity.From the pseudocode of the IMOA,the“while”loop between line 3 and line 27 is the main process,in which the“for”loop between line 4 and line 11 needs the most computing effort.That means the computational complexity in the worst case is mainly determined by the“for”loop.Hence,we first compute the computational complexity in the worst case for each step in the“for”loop.

For line 5:O(nmax|Ki|)

For line 6:O(nmax|Ki|)

For line 7:O(mn2(max|Ki|)2)

For line 8:O(1)

For line 9:O(popsize)

For line 10:O(popsize·n·max|Ki|)

Thus,the total computational complexity for the IMOA in the worst case can be calculated as follows.

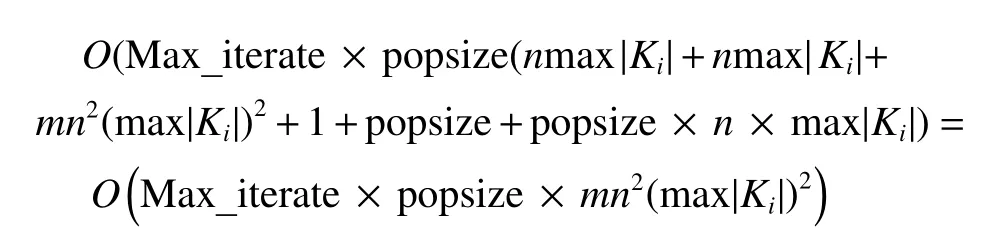
It can be concluded that the computational complexity for the IMOA in the worst case is proportional to the maximal iteration (i.e.,Max_iterate),the population size(i.e.,popsize),the machine amount (i.e.,m),the square of the job amount (i.e.,n2) and the square of the maximal operation amount (i.e.,(max|Ki|)2).

4.Case study

4.1 Design of experiments

4.1.1 Environment configuration

The approach is compiled and run in Intel(R) Core i54210U 1.70 GHz CPU,8.00 G RAM,Win 8.1 64 32-bit operating system,and the Python 3.7 programming language and Pycharm programming environment.

Data from Novas [10],Zhao et al.[26]and Defersha et al.[27]are used as test data.By adjusting the parameters,the processing time of Novas [10]is reduced by 20 times.The instances data is shown in Table 3.

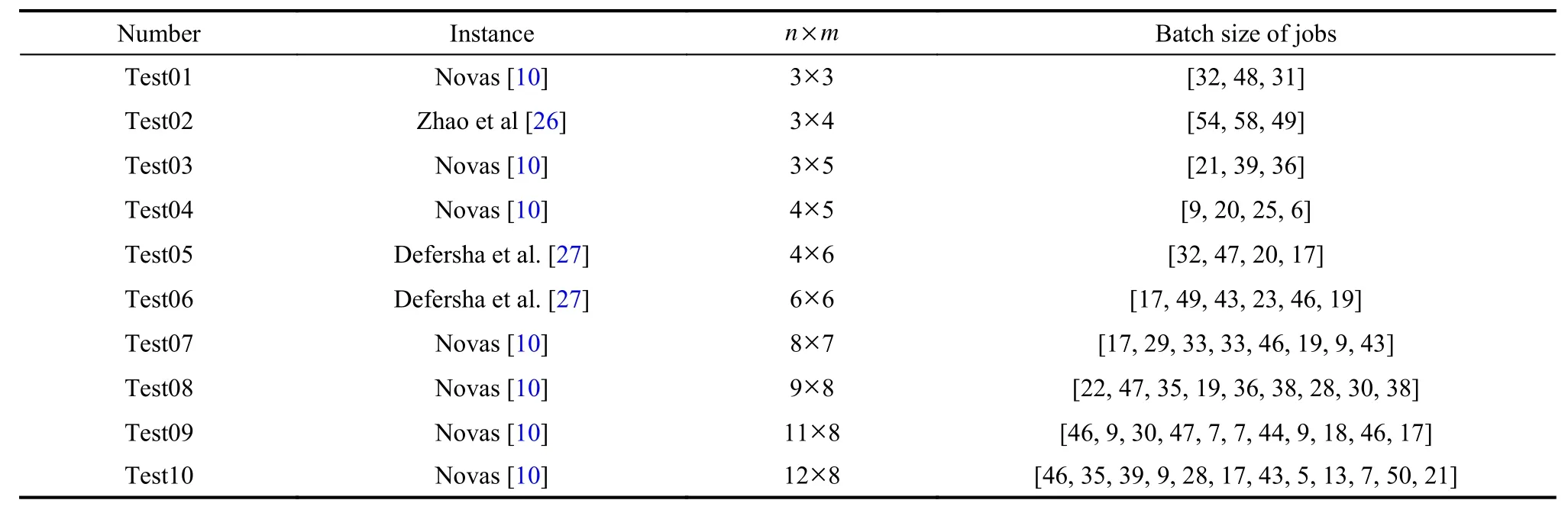
Table 3 The instances

4.1.2 Purpose of experiments

In order to verify the performance of the proposed algorithm in solving FJSP-VB,we carry out the following five experiments.

Experiment 1Parameter setting experiment is carried out to determine the best parameter setting of the crossover probability pc,the mutation probability pm and the number of domain weight vectors R.

Experiment 2The distribution performance experiment of IMOA for solving multi-objective FJSP-VB is carried out to analyze the distribution performance of the Pareto solutions with the instances proposed by Zhao et al.[26].

Experiment 3The batching mode (i.e.,the equal batch size and the variable batch size) comparison experiment is carried out to verify the advantages and disadvantages of the proposed IMOA with the two batching modes.

Experiment 4BOA-IS performance experiment is carried out to verify the effectiveness of BOA-IS in adjusting the batch size of the scheduling solution.

Experiment 5The algorithm performance experiment is carried out to verify the performance of IMOA in solving the multi-objective FJSP-VB.The algorithm is compared with the non-dominated sorting genetic algorithm-II (NSGA-II) [2]and the multi-objective differential evolution (MODE) algorithm [28].NSGA-II and MODE algorithms have good performance in solving multi-objective problems.Therefore,by comparing with NSGA-II and MODE algorithms,the performance of the proposed IMOA can be verified in solving this problem.

4.2 Results of experiments

In Experiment 1,in order to determine the optimal parameters of the crossover probability pc,the mutation probability pm and the threshold R in the algorithm,the hypervolume index (HV),the independent dominating region of the hypervolume index (IHV) and the inverse generational distance (IGD) are taken as the objectives.Take the instance Test02 as the test data,N=100 and Max_iterate=50.The results are shown in Table 4.

In order to analyze the above data clearly,take the mean value of the current objective under the condition that other objectives remain unchanged (see Table 5).

It can be concluded from Table 5 that when the cross probability pc is 0.9 and the mutation probability pm is 0.1,the three objectives are the best.When R is 0.1,HV is the best and when R is 0.15,IHV and IGD are the best.Therefore,pc,pm and R are set as 0.9,0.1 and 0.15,respectively.

In Experiment 2,compare the MOEA/D with modified IMOA and verify the distribution performance of IMOA in terms of the number of Pareto solutions,HV and IHV.Still take Test02 as the test data and the results of running 10 times are shown in Table 6.

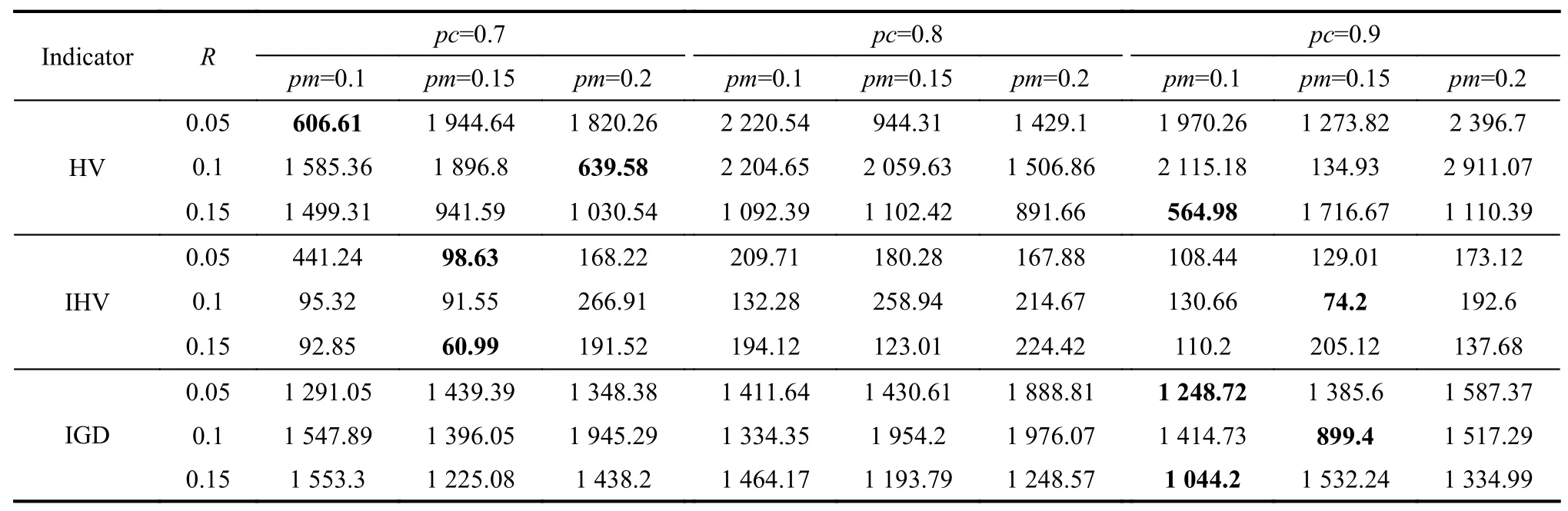
Table 4 Results

Table 5 Analyzed results

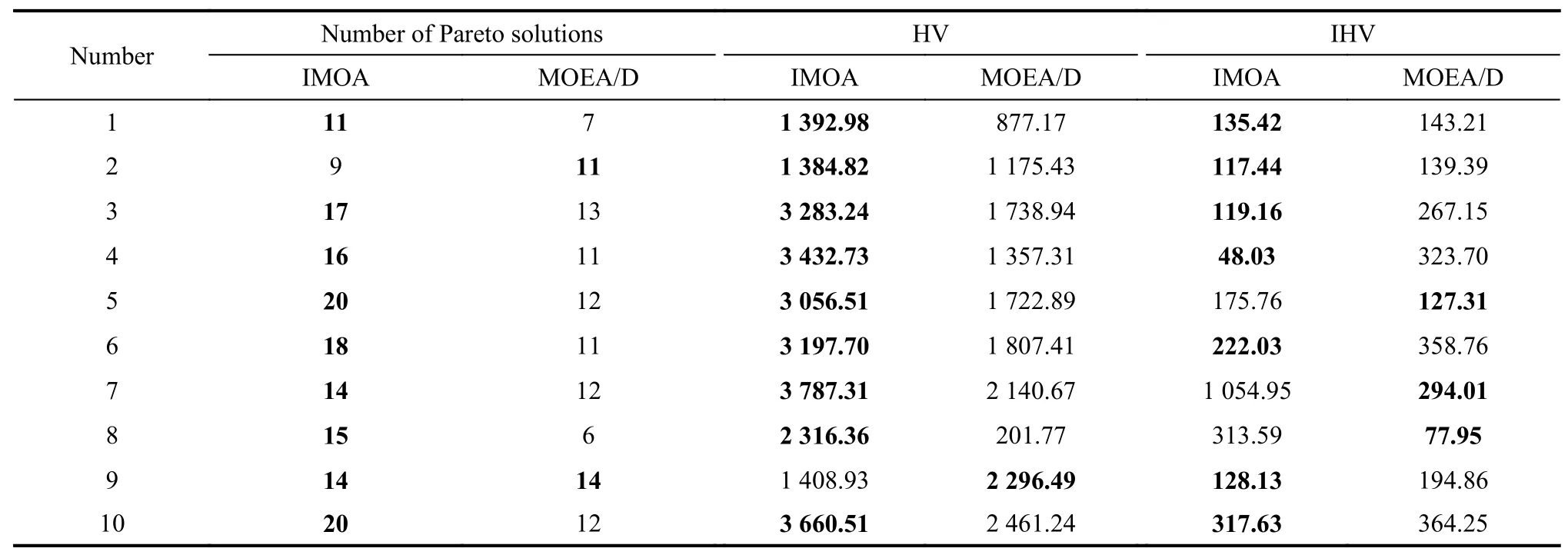
Table 6 Results of the distributed performance experiment

It can be seen from Table 6 that the number of Pareto solutions obtained by IMOA is more than that by MOEA/D,i.e.,IMOA outperforms for eight times.Hence the diversity of solutions obtained by IMOA is better than that by MOEA/D.The HV obtained by IMOA is better than that by MOEA/D,i.e.,IMOA outperforms for nine times.Therefore,the expansion of solutions obtained by IMOA are better than those by MOEA/D,respectively.IHV obtained by IMOA is better than that by MOEA/D,i.e.,IMOA outperforms for seven times.Hence,the uniformity of solutions obtained by IMOA is better than that by MOEA/D.From the view of statistical analysis,it canbe concluded that the IMOA outperforms MOEA/D in terms of the distribution of the solutions.

In Experiment 3,in order to compare quantitatively the results of equal batching and variable batching,the Pareto solutions obtained by two modes are normalized first,and then calculate the average value [29].Equation (18) is for normalization,and (19) is for calculating the mean value.

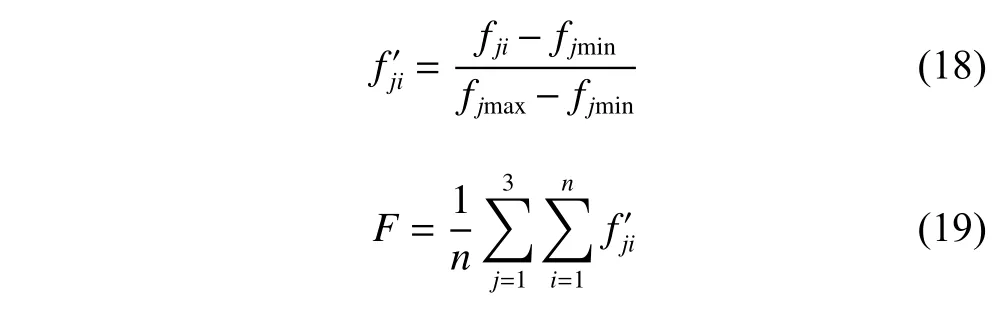
Among them,fjminand fjmaxdenote the minimum and maximum values of the objective j in the Pareto solution set,respectively. fjirepresents the jth objective of the ith Pareto solution;indicates the normalized fji;F represents the average of the sum value of all objectives after normalization.The Wilcoxon rank sum test is used to analyze the results.The hypothesis is that there is no significant difference between the two batching methods.

The results are shown in Table 7.For the ten instances,the results of the variable batching are better than those of the equal batching.When the significance level is set as α=0.05,the z value of the standard normal distribution is 2.608,which is larger than the upper critical value of 1.645 under the significance level.Hence,the original hypothesis is rejected and the experimental results produced by the two batching methods are significantly different.Therefore,it can be concluded that the results obtained by the IMOA using the variable batching dominate the results obtained by the IMOA using equal batching.

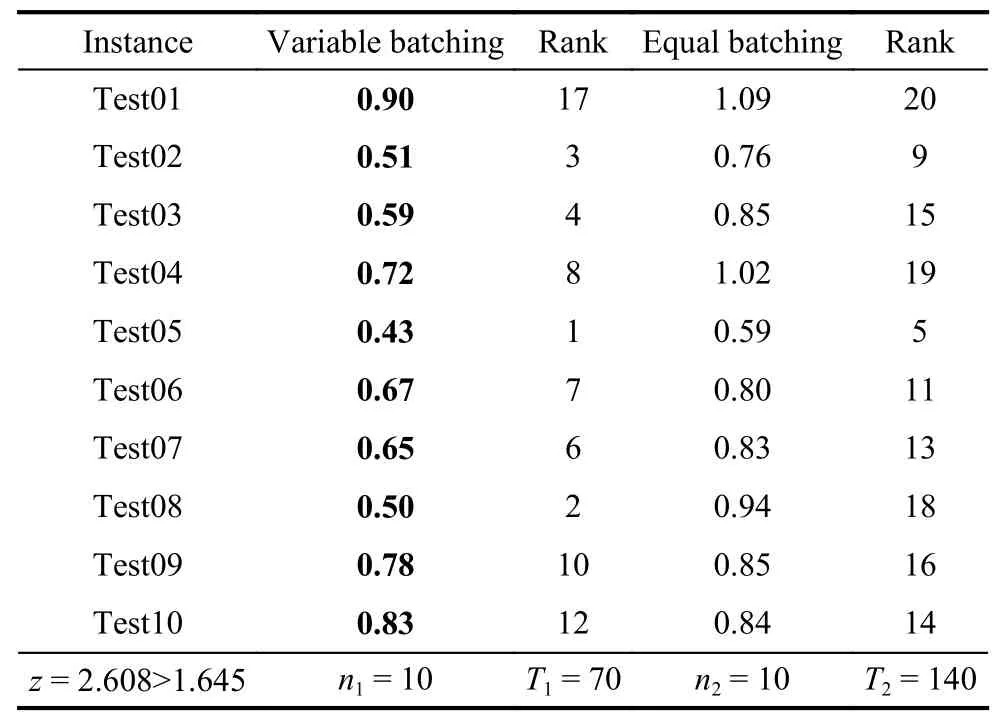
Table 7 Comparison of experimental results

In Experiment 4,ten experiments are run with the test case proposed by Zhao et al.[26].Compare the IMOA integrating BOA-IS with the IMOA integrating GEM.The Pareto solutions are dotted in Fig.11 for each run.The results obtained with BOA-IS are dotted by red star and the results obtained with GEM are dotted by blue balls.

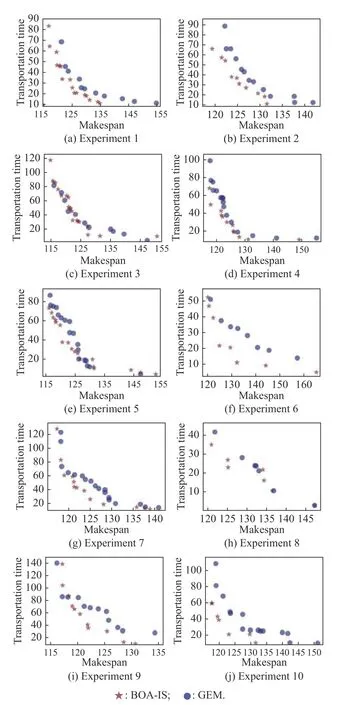
Fig.11 Comparison of Pareto solutions

In order to further analyze the Pareto solutions obtained by BOA-IS and GEM,select the typical Pareto solution obtained with the two algorithms,respectively.In each running result,for the same batching and batch size,an optimal Pareto solution is selected from the Pareto solutions obtained by the GEM algorithm according to thepriority order of completion time and transportation time.The optimal Pareto solution is found in the Pareto solutions obtained by BOA-IS with the priority that the completion time and transportation time are better than the typical Pareto solutions.The typical Pareto solutions obtained by the two decoding algorithms are shown in Table 8.

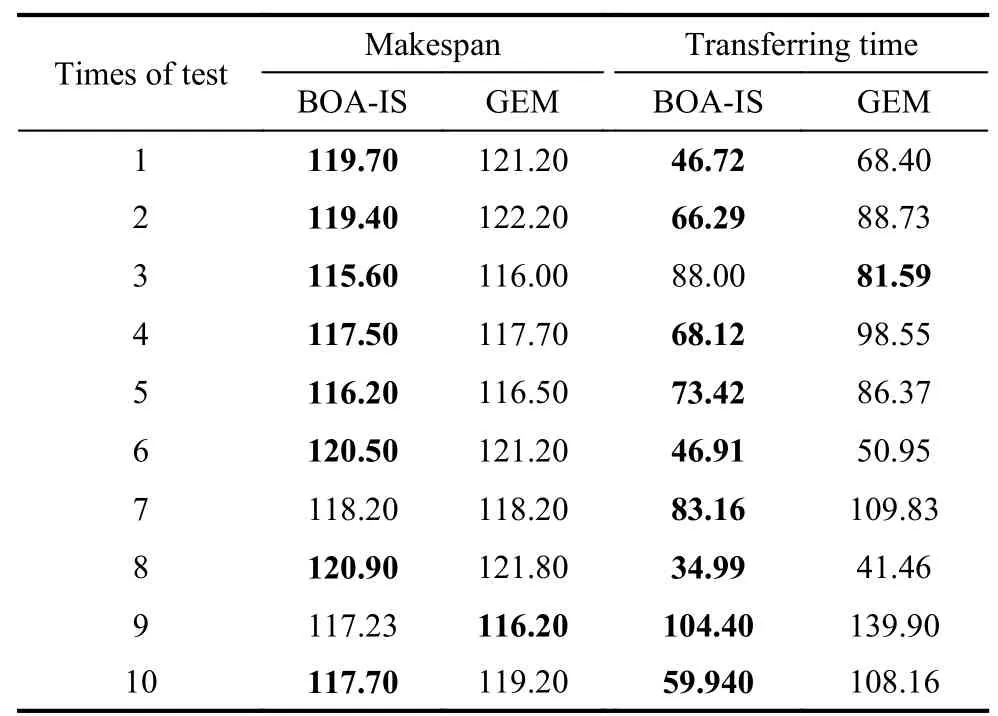
Table 8 Comparison of BOA-IS and GEM

From the distribution of Pareto solutions in Fig.11,it can be concluded that the BOA-IS dominates the GEM.Analyze the experimental results in Table 8,it can be found that only the typical Pareto solution obtained by the GEM in the 9th experiment is better than that by BOA-IS in terms of the completion time.In terms of the transferring time,only in the third experiment,the Pareto solution obtained by the GEM is better than that of BOA-IS.Only in the 3rd and the 9th experiments,BOA-IS and GEM dominate each other in the 10th experiment.Therefore,for the multi-objective FJSP-VB,BOA-IS outperforms GEM from a statistical point of view.

In Experiment 5,in order to compare IMOA,MODE and NSGA-II more intuitively,calculate the mean value of Pareto solutions generated by IMOA,MODE and NSGA-II and report them in Table 9.It can be seen from Table 9 that the results obtained by IMOA are better than those obtained by NSGA-II in most instances except for the 2nd and the 4th experiments,in which IMOA and NSGA-II dominate each other.Except for the 5th and the 7th tests,the results obtained by IMOA are better than those obtained by MODE.

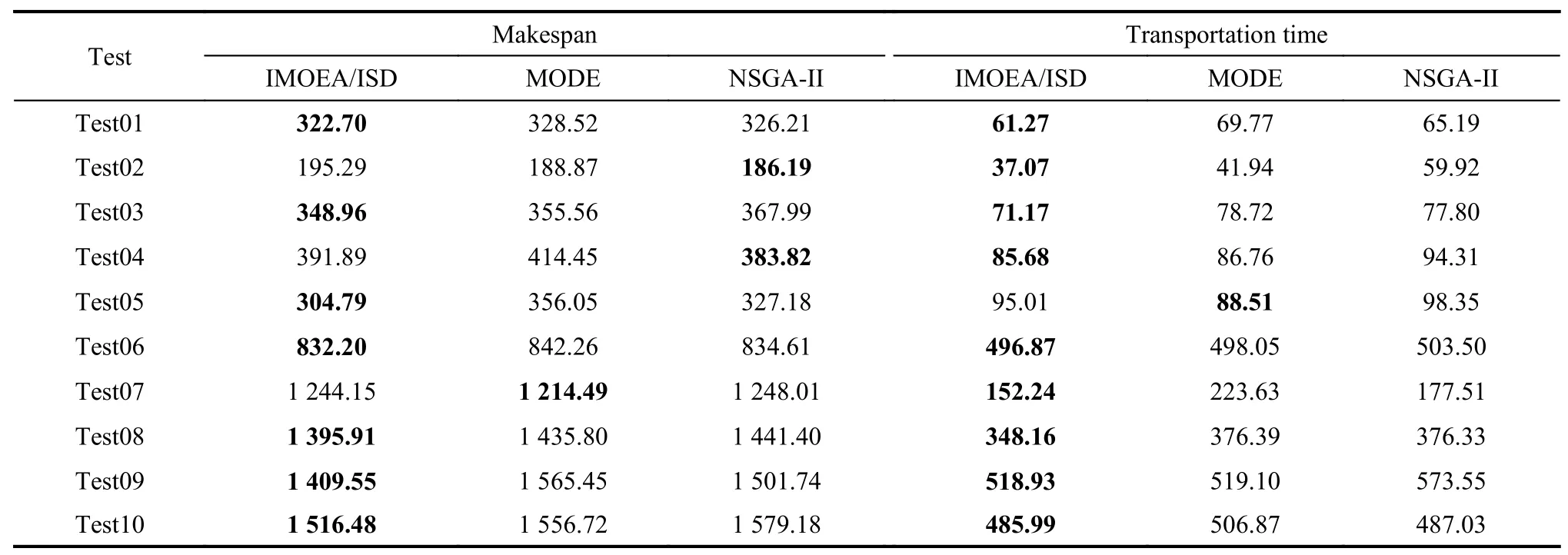
Table 9 Comparison of three algorithms

5.Conclusions

This paper studies FJSP-VB,which improves the MOEA/D and proposes an IMOA.Firstly,two strategies are designed to control the updating of the individuals:one is to update neighbors with a threshold and the other is to introduce the clustering algorithm to dynamically increase the diversity of the population.Secondly,in order to further optimize the batch size of each batch of a job,this paper proposes a batch optimization algorithm on the basis of the inverse scheduling to optimize the batch size of each sub-batch.Finally,in order to verify the performance of the proposed algorithm,five groups of experiments are carried out.The results show that the proposed algorithm solves FJSP-VB effectively.

In the FJSP-VB,challenges include optimization of the batch number and the batch size of each job and reduction of the computing complexity of the algorithm are worthy of in-depth investigation.Besides,although there are many studies on the optimization algorithm for solving the flexible job shop batch scheduling,our future work aims to integrate heuristics and self-learning to improve the performance of the algorithm,and study the uncertainties [30]in the scheduling problem.