基于非注入法PMSM无位置传感器控制策略研究
谢曼莎
(北京信息科技大学自动化学院,北京 100192)
0 引 言
永磁同步电机(以下简称PMSM)无位置传感器控制是基于转子位置的自检测技术,利用绕组参数方程中含有与电机转子位置有关的量,通过直接计算、参数辨识、间接测量等方法[1-3],提取出转子的位置和转速。与有位置传感器控制相比,无位置传感器控制具有精度高、控制成本低、体积小、抗干扰能力强等优点[4]。电机的低速起动问题一直是研究的热点,当电机运行于低速段时,由于转速低,电机激励出的与电机位置相关的的信号量小,在采样过程中难以精确获取,使得控制可靠性降低,同时增加采样负担。目前,PMSM低速运行常采用高频注入法等,高频注入法由于注入了高频信号,增大了信噪比,给电机运行带来了高频噪声;磁链观测法计算量大,计算周期长,且相电压和电流中含有较大的干扰信号,很少采用;基波模型法依赖于基波激励的电机数学模型,易受电机参数影响,对电机参数的鲁棒性能要求高。
综上,本文利用PMSM定子电流的导数在零电压矢量区间携带电机转子位置信息的特性,设计了一种非注入法的电机转子位置估算方案,获取电机转子位置信息。
1 基于非注入法在零电压矢量区间的转子位置估计原理
基于电流导数在零矢量区间的转子位置估计原理是在零电压矢量区间[5-8],通过检测d、q轴电流导数,构建合适的转子位置检测模块,提取出转子位置信息,利用电流转速双闭环将位置误差收敛至零,估计电机的实际转子位置。
PMSM在同步旋转坐标系下的电压方程可以表示:
(1)
式中:ud,uq分别为d、q轴电压;R为定子电阻;p为微分算子;Ld,Lq分别为d、q轴电感;id,iq分别为d、q轴电流;ωr为转速;ψf为磁通。
在零电压矢量区间内,电机端电压为零,ud=uq=0,由式(1)可以写成:
(2)
假设一个估计d,q轴系,记为d-qest,估计轴系电角度为θest,估计轴系与实际轴系之间的转子角度误差为θerr,θerr=θest-θe,式(2)可以写成:
(3)
式中:等式左边为估计的d轴电流导数;θest为估计轴系电角度;θerr为估计轴系与实际轴系之间的转子角度误差;idest,iqest分别为估计的d,q轴电流。
式(3)表明估计的d轴电流导数表达式是电机转子位置的函数,这是此算法的理论基础。
2 零矢量区间的转子位置信息提取方法
由式(3),当转子位置误差趋近于零时,以下条件满足:
cosθerr→1,sin(2θerr)→2θerr
(4)
由此,可将式(3)简化:
(5)
当转子位置误差等于零时,式(5)简化:
(6)
从式(6)可以得出,当角度误差θerr=0时,估计的d轴电流导数仅与定子电阻、d轴电感和估计的d轴电流有关,且需要保持d轴电流为一不为零的常数。对于给定的d轴电流,当电机估计转子位置稳定跟踪上实际转子位置时,式(6)等式右边为一常数。可以利用式(6)来构造转子位置检测模块,将转子位置误差收敛至零,获取电机的转子实际位置,检测模块结构框图如图1所示。
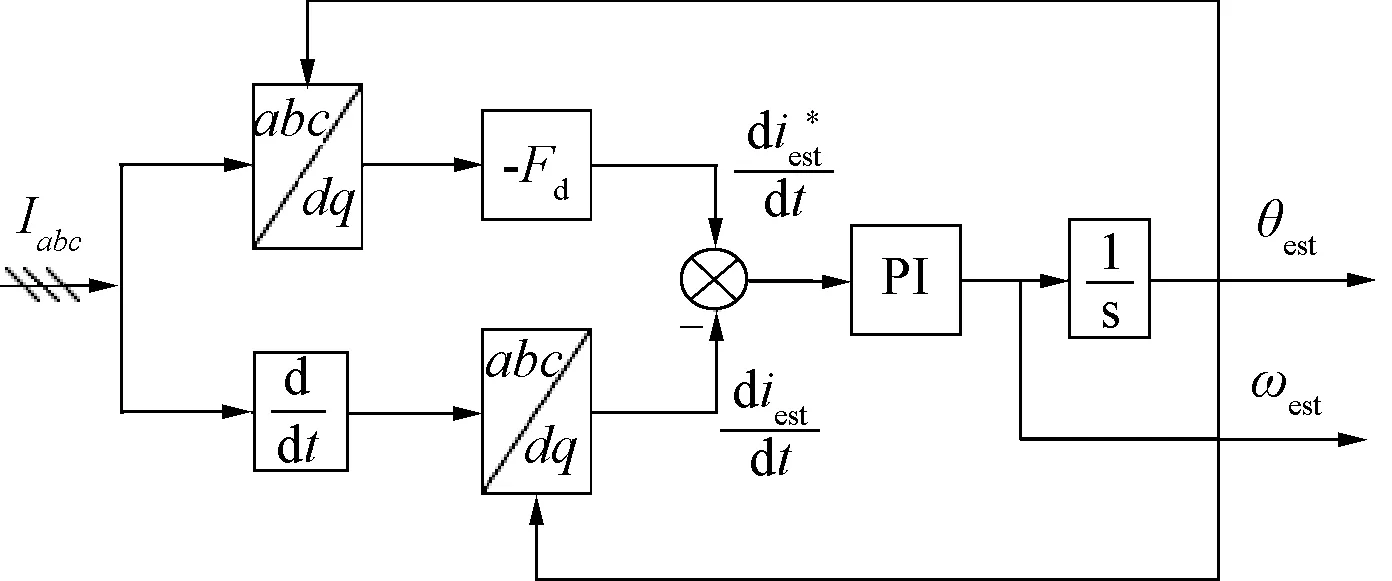
图1 转子位置估计模块结构框图
3 仿真结果及分析
根据上文中的电机参数推导结果,在式(6)的基础上,构造检测模块,获取电机的角度位置,基于电流导数法在零电压矢量区间的转子位置估计控制系统结构框图,如图2所示。
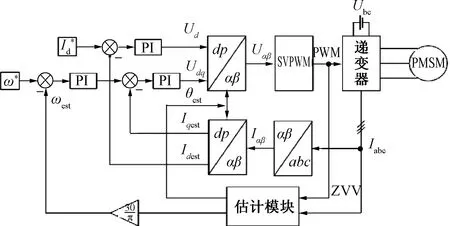
图2 基于电流导数法在零矢量区间的转子位置估计控制系统结构框图
图2检测模块的功能是采样的电压矢量是在零矢量区间内对三相电流进行采样,采样结果变换到d、q轴系下,再将d轴电流导数经PI调节,将电机的电角度与估计电角度之差收敛至零,获取电机的实际电角度。
给定转速为100 r/min,给定d轴电流为-5 A,仿真用PMSM参数如表1所示。

表1 仿真用PMSM参数
为验证此算法在低速起动的性能,给定负载为10 N·m时,给定转速为100 r/min,得到的部分仿真结果如图3~图6所示。
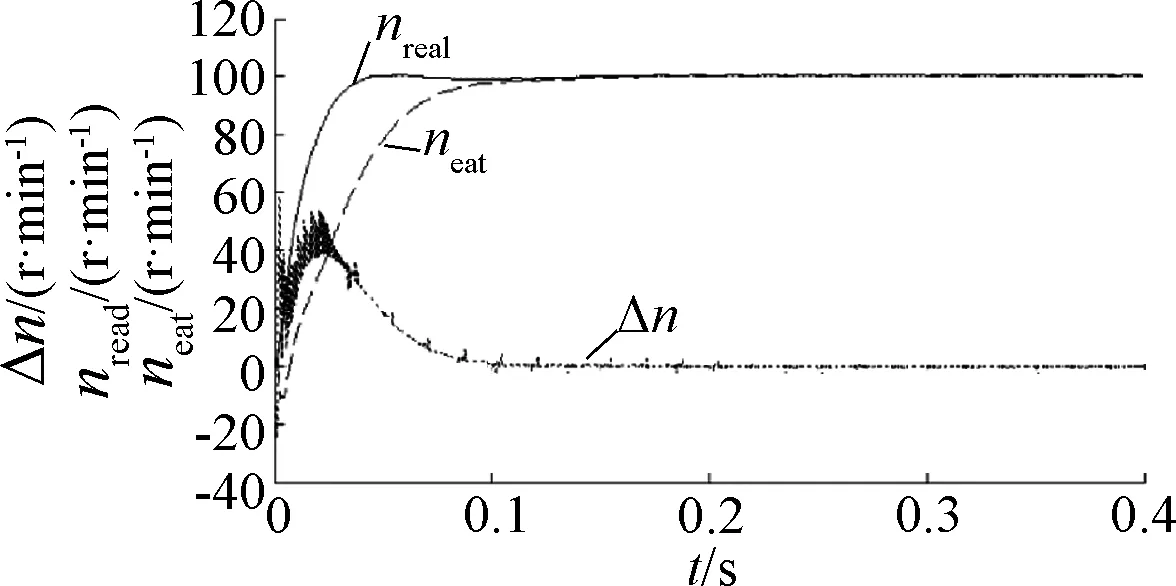
图3 实际转速nreal、估计转速nect、转速误差Δn
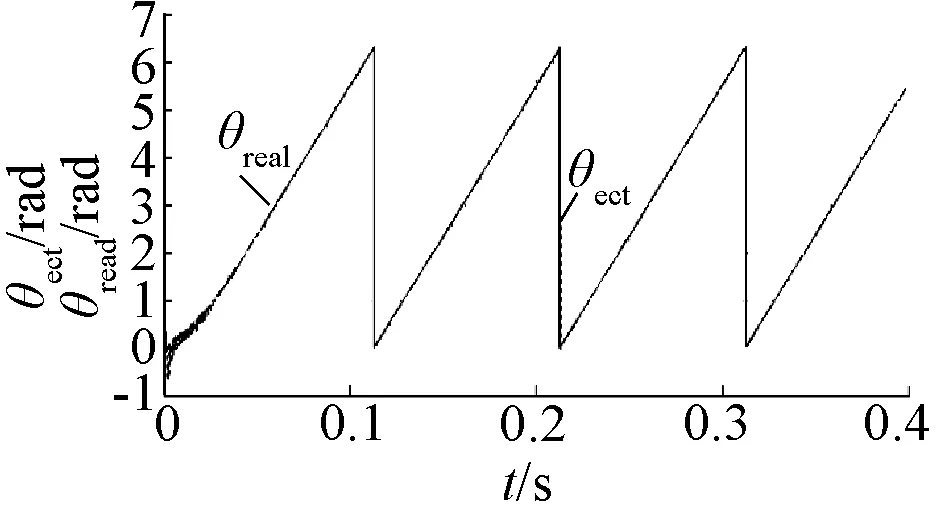
图4 转子实际位置θreal、估计位置θect
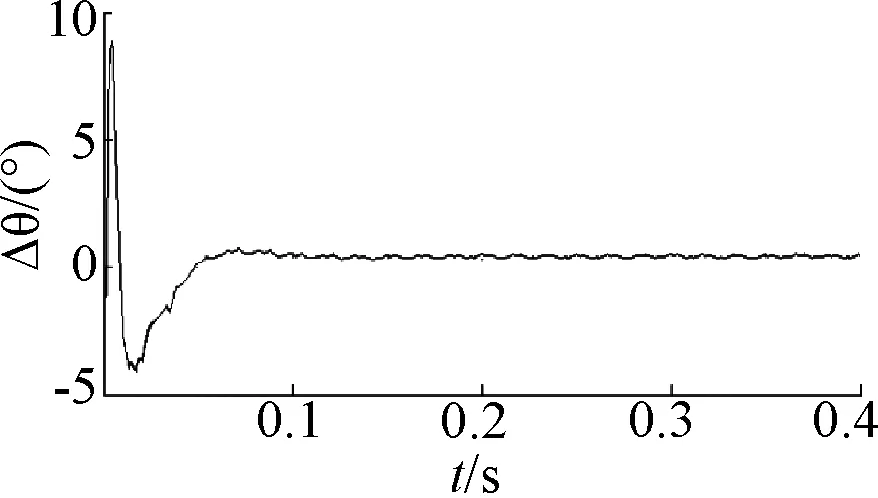
图5 转子位置误差Δθ
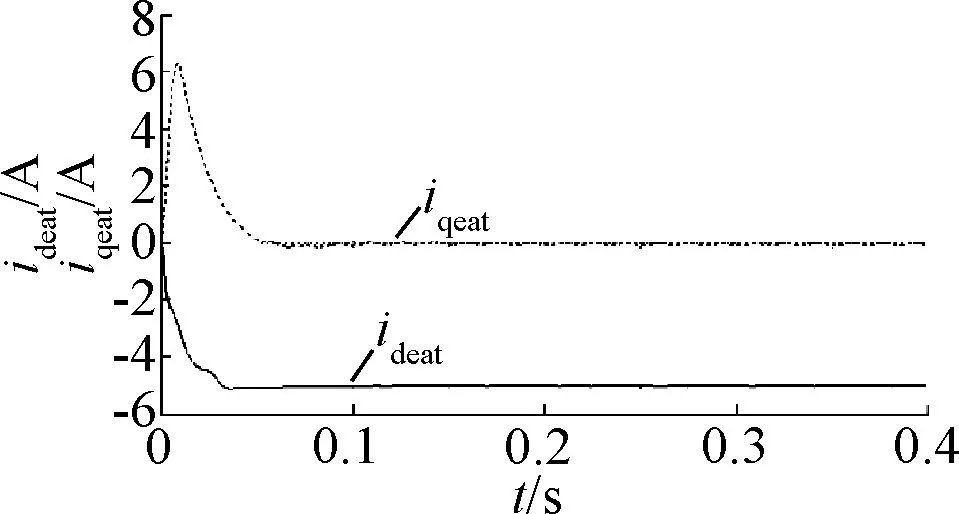
图6 估计的d、q轴电流
以上仿真结果,约在t=0.1 s时达到给定转速,动态过程中转速无超调、无振荡,具有良好的动态响应速度;随着电机转速的上升,约在t=0.05 s转子位置误差收敛至趋近于零的某一值,稳态时转子位置误差约为0.4°,具有良好的稳态跟踪性能。
4 结 语
本文研究并推导了电流导数法转子位置估计原理,在MATLAB/Simulink仿真软件环境下对此算法进行了仿真验证,验证结果显示,利用d轴电流导数估计转子位置在稳态精度、动态响应等方面都显示出了良好的控制性能。

