基于开绕组的BLDCM DTC换相转矩脉动抑制方法研究

张永民，杨建飞,2，金 振，邱 鑫,2，陈秋仲，吕 润，周 阳

(1.南京师范大学 电气与自动化工程学院，南京 210023；2.南京智能高端装备产业研究院有限公司，南京 210042；3.国电南瑞集团有限公司，南京 211100)

0 引 言

无刷直流电动机(以下简称BLDCM)因其控制简单、效率高和体积相对较小等优点，被广泛应用于航空航天等领域[1-3]，但是转矩脉动问题制约着BLDCM在高精度位置伺服系统以及高性能调速系统的应用。转矩脉动主要分为换相转矩脉动、PWM斩波引起的转矩脉动和非理想反电动势引起的转矩脉动这三种。

为获得最大转矩输出，BLDCM直接转矩控制(以下简称DTC)系统常采用两相导通模式[4]。两相导通模式下存在换相期间较大关断相续流问题，这会引起较大的转矩脉动[5]。文献[6]首次分析了在传统星形连接BLDCM中，换相期间无法使电流快速跃变就会引起一定的换相转矩脉动。文献[7]进一步解释了转矩脉动产生的根本原因是电流交替变换速度有差异，如果保持交替速度一致，则可以消除换相转矩脉动。文献[8]提出了一种三相脉宽调制方案来降低换相转矩脉动，此方法的换相时间不需要计算且不受限于电机参数，但是硬件成本较高，体积较大。文献[9]将交流电机常用的坐标变换引入到BLDCM DTC系统换相期间进行分析，实现了在全速范围内换相转矩脉动和换相时间的相互协调。但该方法计算量较大，增大了控制器设计的难度。文献[10]通过引入新型零电压矢量并借助占空比调制的策略来实现换相转矩脉动的抑制，虽然抑制效果较好，但占空比调制策略计算量依旧过大且控制复杂。文献[11]通过基于电流预测的占空比调制方法来实现转矩脉动的抑制，但是控制效果并不如采用单一占空比调制策略好。为实现电流交替变换速度一致，除上述提到的控制方法外，也可通过调节直流母线电压实现[12]。改变母线电压一般通过改变硬件拓扑结构以实现电压补偿。文献[13]通过将CUK变换器与逆变器电路相结合，利用占空比调制策略实现母线电压的调节，如图1所示。

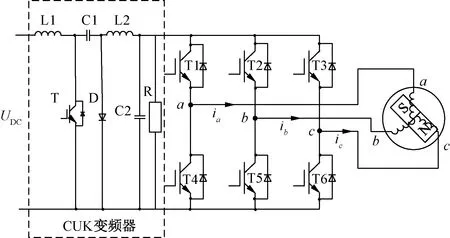
图1 基于 CUK 变换器的 BLDCM驱动系统

当前，针对星形BLDCM转矩脉动的研究主要分为电流控制法和控制拓扑改进法，电流控制法使得控制更加复杂；控制拓扑的改进只是一定程度上增加了电压矢量的个数，但依旧受限于星形连接结构和桥式拓扑。因此，需要将BLDCM绕组断开，来研究共直流母线下多维度电压矢量对转矩脉动的影响。

开绕组BLDCM拥有对每相绕组独立控制，并且电压矢量多维度等优点[14]。浙江大学孙丹教授对开绕组常使用的几种拓扑结构、三电平下的电压矢量分布以及相关控制技术做了总结[15]。西北工业大学罗玲教授对开绕组BLDCM的8种运行状态做了大致分析[16]，其中单向导通有3种，正、反双向导通有5种。文献[17]采用重叠换相法来抑制换相转矩脉动，并推导了关断相施加电压和延迟关断时间公式。重叠换相法控制过于复杂，并且对电流计算过分依赖于传感器的精度，对硬件精度有很高的要求。

本文在分析开绕组多维度电压矢量的基础上，研究包含新型零电压矢量在内的多种电压矢量组合对BLDCM DTC换相电流和换相转矩脉动的影响，提出对传统星形连接BLDCM DTC存在的换相转矩脉动的抑制方法。相比于上述传统重叠换相等方法，该方法不需要对电流变化时做过于复杂的公式变换，且不需要过分依赖于传感器精度，操作简便，控制更加简单。

1 开绕组BLDCM模型分析

1.1 共直流母线控制拓扑分析

相比于传统星形连接BLDCM采用的桥式拓扑，开绕组BLDCM的控制拓扑采用两组逆变器，每组3对开关管共12个开关管。常见的拓扑分为共直流母线和独立母线两种，图2和图3分别为共直流母线和独立母线拓扑结构图。由于共母线结构共用一个电源，故其结构更为简单，成本更低，适用于对空间要求较大的场合[18]。

图2 共直流母线开绕组BLDCM驱动结构图

图3 独立母线开绕组BLDCM驱动结构图

开绕组BLDCM采用共直流母线拓扑结构具有以下特点：

1)每相绕组可以独立控制，控制更加灵活。

2)电机由两组逆变器供电，可提高整体电机系统的容量。

3)拥有三电平特性，可以提高输出电能质量。

4)相较于桥式拓扑电压矢量更加多维，且具有一定的容错能力。

由图2可知，电机绕组每相电压为两个逆变器输出电压之差，故电压方程可以写成：

(1)

式中：Smn(m=a,b,c，n=1,2)表示每一相上桥臂的开关状态，当Smn=1时，对应某一相桥臂中上桥臂导通，当Smn=0时，对应某一相桥臂中下桥臂导通；Udc表示为直流母线电压；u00′表示为两组逆变器之间的对地电压差值。

每相电压一共有Udc，0，-Udc三种输出状态，因此共直流母线拓扑具有三电平特性。又因为共直流母线将两组逆变器并联于同一直流母线，造成两个逆变器共地回路，故：

u0=u0'

(2)

式(1)可以写成：

(3)

1.2 电机本体数学模型分析

与传统星形连接BLDCM不同，开绕组BLDCM是将传统星形连接BLDCM的绕组中性点打开，电机特性发生了一定的变换。

1.2.1 电压平衡方程

开绕组结构取消了中性点，因此相电压平衡方程中没有中性点电压，在不考虑开关管器件压降的前提下，相绕组电压平衡方程可表示：

(4)

式中：UA，UB和UC为三相绕组电压；相电阻统一表示为R；iA，iB和iC为三相绕组电流；相电感统一表示为L；绕组互感统一表示为M；eA，eB和eC为三相反电动势。

1.2.2 反电动势方程

开绕组BLDCM反电动势为平顶宽度为120°电角度的梯形波，其具有非正弦特性。梯形波幅值可以表示：

E=CeΦδn

(5)

式中：n为电机转速；Φδ为气隙磁通；Ce为电动势常数。

1.2.3 电流方程

当电机平稳运行时，电流变换率为0，则从式(4)可以得出绕组相电流可以表示：

(6)

又因为电机没有中性点，故三相绕组电流之和不为0，可以表示：

I=iA+iB+iC≠0

(7)

1.2.4 电磁转矩方程

电机电磁转矩方程可以表示：

(8)

式中：ω为转子机械角速度；Te为电磁转矩。

1.2.5 运动方程

运动方程体现了电磁转矩、负载转矩和转速三者之间的关系如下：

(9)

式中：TL为负载转矩；B为粘滞摩擦系数；J为转动惯量。

2 电压矢量分析

2.1 传统星形连接BLDCM DTC新型零电压矢量分析

2005年英国谢菲尔德大学的诸自强教授等人提出了六个空间电压矢量的概念，并将开关管全关断矢量(000000)定义为零电压矢量，这使得BLDCM DTC理论逐步进入正轨[19]。所提空间电压矢量如图4所示。但全关断矢量的作用效果相当于反矢量，并不能真实反映零电压矢量对转矩等电机特性的影响[20]。

图4 两相导通合成空间电压矢量图

在传统星形连接BLDCM DTC两相导通方式下，能使得合成电压矢量等于零的电压矢量定义为新型零电压矢量。以扇区S5为例，此时a、b两相导通，零电压矢量的定义方式有两种：一是利用上二管构成新型零电压矢量(101000)，等效电路如图5所示；二是利用下二管构成新型零电压矢量(010100)，等效电路如图6所示。

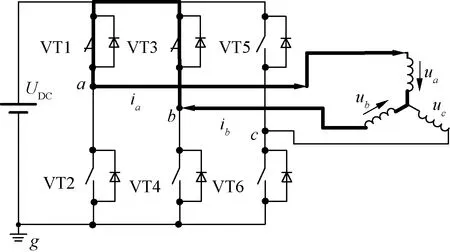
图5 上二管零电压矢量V72(101000)作用等效电路图

图6 下二管零电压矢量V02(010100)作用等效电路图

与上述分析类似，其他扇区也存在着两种新型零电压矢量定义，矢量分布如表1所示。

表1 各扇区新型零电压矢量分布表

2.2 开绕组BLDCM DTC电压矢量分析

单组逆变器可以有6个正电压矢量和2个零电压矢量，因此逆变器的合成电压矢量有64种。排除冗余项，实际有18个不同的有效正电压矢量和1个零电压矢量，电压矢量分布图如图7所示[21]。

图7 开绕组BLDCM DTC电压矢量分布图

由表1可知，单组逆变器拥有6个新型零电压矢量，其大小为0。下面对开绕组BLDCM DTC新型零电压矢量做具体矢量合成过程分析，如图8所示。

图8 逆变器1和逆变器2对应的电压矢量图

将两组逆变器的对应矢量进行相减就可以完成矢量合成，合成的新型零电压矢量共有42种，如图9所示，主要分为新型零电压矢量和新型零电压矢量合成：62=36种；和正电压矢量自身合成的6种新型零电压矢量。42种开关管状态及其合成的新型零电压矢量如表2所示。

图9 合成电压矢量图

表2 42种开关状态与新型零电压矢量

3 转矩脉动仿真分析

3.1 传统星形连接BLDCM DTC转矩脉动仿真

仿真电机参数如表3所示，Simulink仿真电路图和转矩电流波形图分别如图10和图11所示。

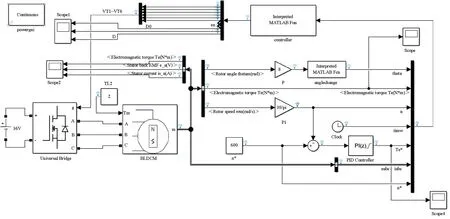
图10 传统星形连接BLDCM DTC仿真电路图

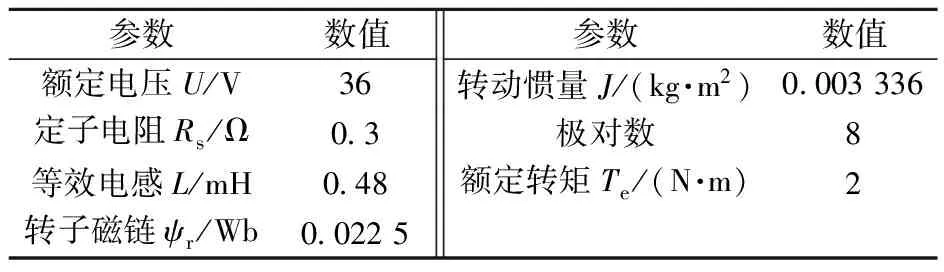
表3 电机参数

从图11可以看出，在电机换相期间换相电流变化较大，同时转矩从0.7 N·m变化到2.3 N·m，转矩脉动均值为1.3 N·m。

图11 传统星形连接仿真电流转矩波形图

3.2 开绕组BLDCM DTC转矩脉动仿真

3.2.1 开绕组BLDCM DTC正矢量控制仿真

图12和图13分别为开绕组BLDCM开环下的仿真电路图和波形图，图14和图15分别为开绕组BLDCM DTC仿真电路图和波形图。电机参数同表3。开环条件下空载时转速可以达到1 780 r/min，加载后稳定在600 r/min，转矩脉动0.35 N·m。闭环系统采用Hall传感器检测转子位置信号，同时通过位置计算来选择合适的正电压矢量(无零电压矢量参与)进行系统控制。闭环系统给定转速1 000 r/min，加载时转速波动在2 r/min，转矩脉动在1.45 N·m。

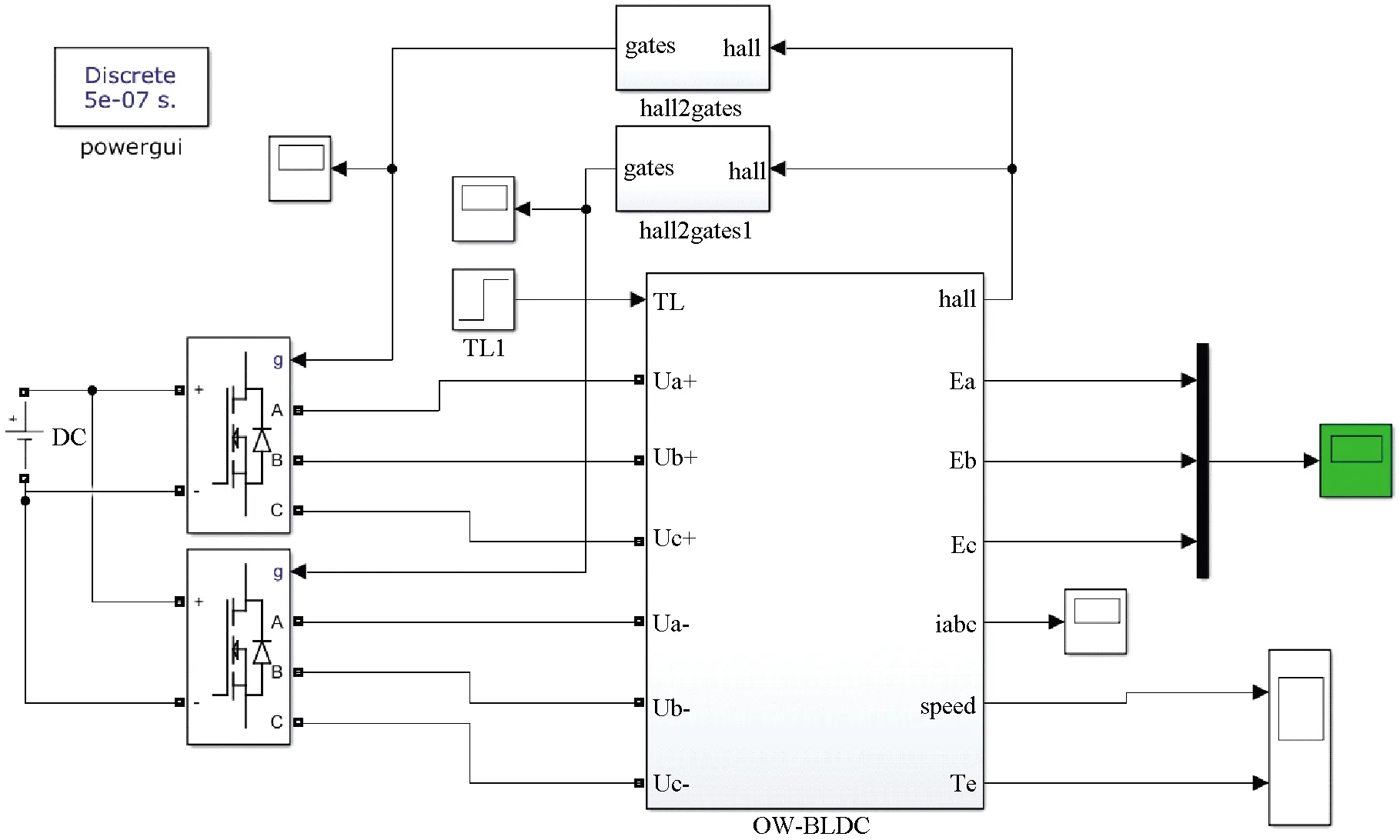
图12 开绕组BLDCM开环控制仿真电路图

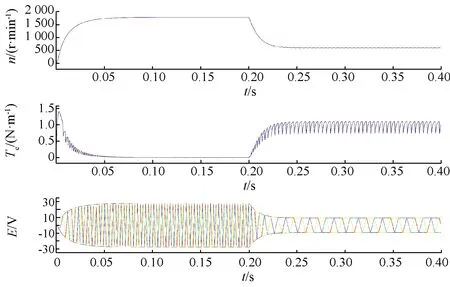
图13 开环转速、转矩和反电动势波形图

图14 开绕组BLDCM DTC仿真电路图

图15 闭环转速、转矩和反电动势波形图

从输出结果可初步看出，开绕组BLDCM DTC在通过传统6扇区参与控制下，具有较为优良的转矩和转速特性。

3.2.2 开绕组BLDCM DTC新型零电压矢量控制仿真

新型零电压矢量需要配合正电压矢量序列才可以参与到BLDCM DTC中。正矢量和新型零电压矢量选择表如表4所示。

表4中，τ为转矩调节器输出标志，τ=1时需要通过正电压矢量来增大转矩，τ=0时需要通过新型零电压矢量来减小转矩。

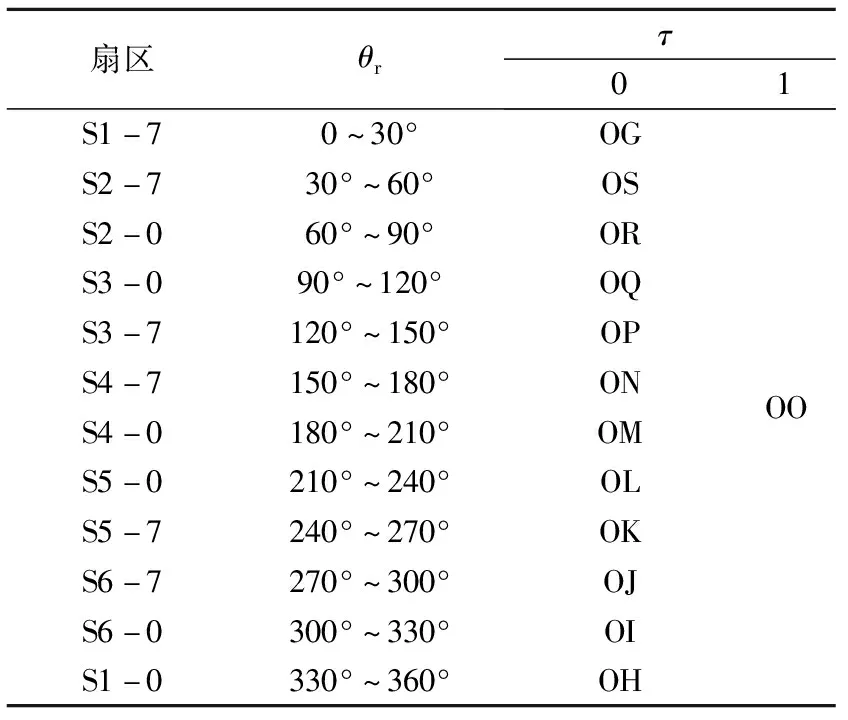
表4 正矢量和新型零电压矢量选择表

为充分探究新型零电压矢量对BLDCM DTC系统性能的影响，需要对控制系统的动态过程进行研究。图16为开绕组BLDCM DTC纯滞环控制框图，转子角度和转速通过计算得出。给定转矩与实际转矩的差值作为转矩内环的输入，输出为τ。τ结合转子角度θr，查询得到合适两组开关管状态，驱动电机运行。

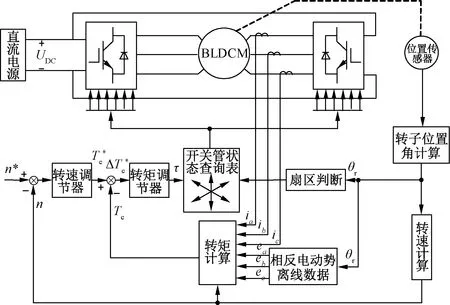
图16 开绕组BLDCM DTC纯转矩环控制框图

图17为开绕组BLDCM DTC新型零电压矢量参与控制的仿真结果波形图。从图17中可以看出，由于换相期间新型零电压矢量的参与，电流从0变化到-1 A，同时转矩从2.9 N·m变化到1.2 N·m，转矩脉动均值为0.8 N·m。相比于传统传统星形连接BLDCM DTC系统，引入新型零电压矢量后，转矩脉动变化率降低了25%。

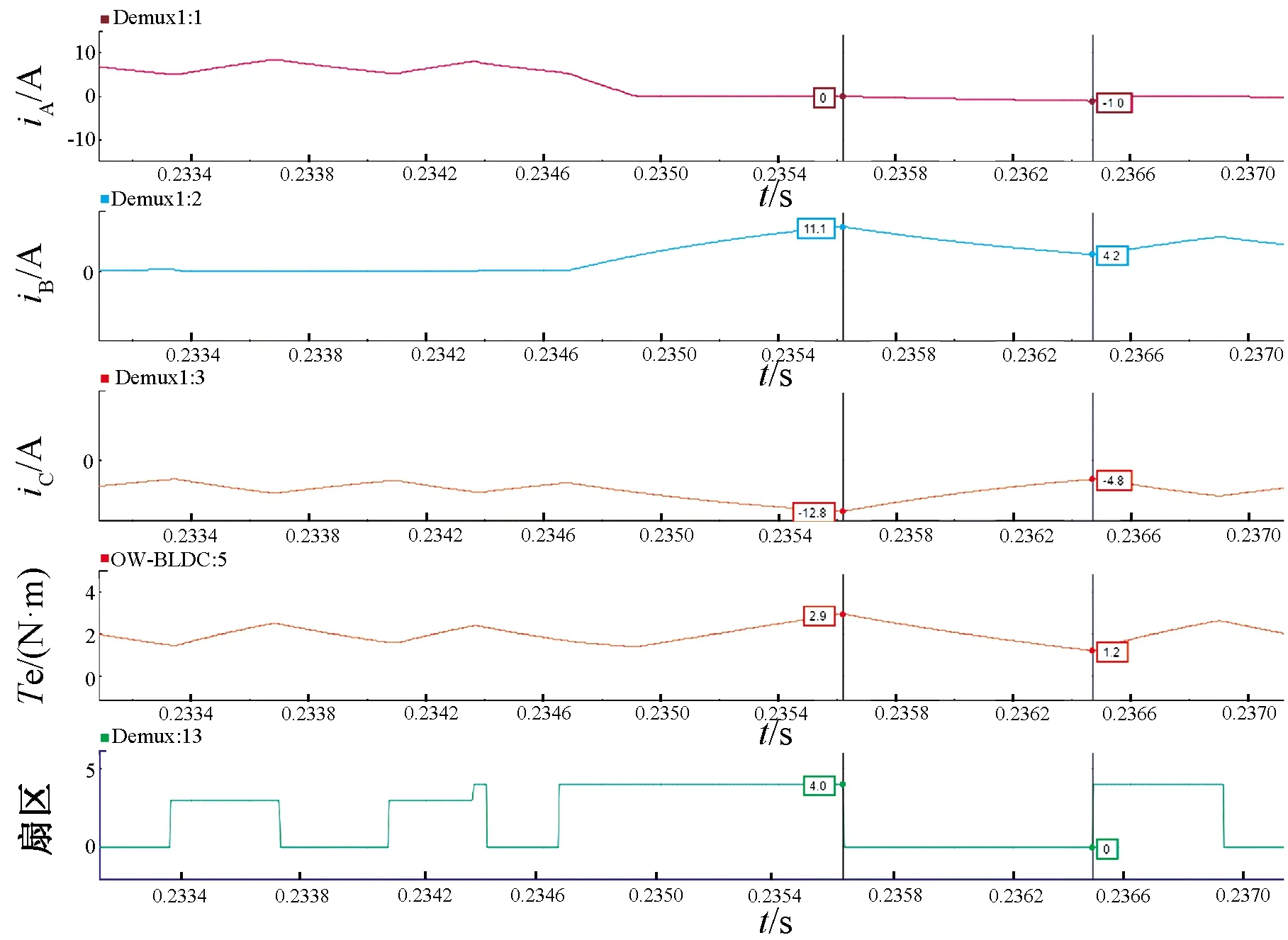
图17 新型零电压矢量参与控制的仿真波形图

4 结 语

本文研究了一种基于开绕组结构的BLDCM DTC系统换相转矩脉动抑制方法。同传统新型连接BLDCM DTC系统转矩脉动抑制方法相比，该方法充分发挥开绕组结构下多维度的电压矢量和每相绕组独立控制的优势，结合新型零电压矢量和正电压矢量达到转矩脉动的抑制效果。与此同时，该方法不需要采用重叠换相法进行复杂的电流计算，不需要过分地依赖传感器精度，较为简单，且适用性较高。仿真结果表明，结合新型零电压矢量和正电压矢量进行控制，可以有效抑制换相期间关断相续流带来的转矩脉动问题，与理论分析一致。