基于布里渊分布式光纤的储液罐变形场重构方法研究
马 涛,丁克勤,舒安庆,刘亚男
(1.武汉工程大学 机电工程学院,武汉 430205;2.中国特种设备检测研究院,北京 100013)
0 引言
应变、变形监测是储液罐安全运行的基础,是不可或缺的部分[1]。储液罐属于典型的薄壳壁结构,在储运过程中会因变形产生疲劳裂纹损伤,很容易发生泄漏事故,导致极其严重的后果[2-3]。对结构应变、变形的实时监测,是储液罐运行状态安全评价的前提[4]。传统的方法主要是以电测的方式为主,例如采用位移计、加速度传感器、GPS(Global Positioning System)和激光位移传感器等方法[5-6]。虽然这些方法对结构的变形监测具有精度高、实时性好的优点,但其主要以激光源为核心,且长期使用激光光源会导致寿命变短,难以满足对大型结构长期有效的监测需求。
大型储液罐在运行过程中,由于地震或不均匀沉降因素的影响,储液罐薄壳壁结构上的应变值超过结构承受的极限而造成结构损坏,所以实时监测结构的应变可以很好地避免此类事故的发生[7-8]。虽然布里渊分布式光纤能够监测出整个储罐的应变数据,但处理数据的过程十分繁琐,因此,有必要采用一种高效的算法,通过提取罐体的局部应变信息,反演出整个结构的变形位移场,为结构的安全评估提供重要依据。在国外,美国航空航天局兰利研究中心Tessler等[9]提出基于最小二乘变分方程的逆向有限元法。常规的有限元分析方法通常是通过已知条件给结构施加载荷或者位移,然后根据计算得出结构的应力应变响应;逆有限元法是指已知量和未知量之间的反演。已知结构的应变响应,然后通过应变响应逆向推导出结构的位移。基于弹性力学Mindlin(考虑横向剪切变形)的厚板理论和最小位能原理,建立反向有限单元,利用最小二乘法方程求解结构应变场与位移场之间的传递函数,解决了应变转换到位移的反向问题[10]。在国内,钱晋武等[11]研究了基于光纤光栅的变形监测和可视化技术,提出了由曲线重建到曲面重建的渐近重构算法,采用四边形网格细分算法连接曲面,并由曲率和弧长信息重建变形曲面。
如何在储液罐薄壳壁结构局部获取的应变数据反演出整个储液罐体结构的位移场,依然是该领域的难题。基于上述分析,本文提出采用布里渊分布式光纤传感器来测量储液罐薄壳壁结构的局部应变信息,通过基于模态叠加原理的算法实现应变-位移转换,对变形曲面进行可视化重构,该方法达到了高效率、高精度监测储液罐薄壳壁结构变形的目的。
1 储油罐薄壳壁板变形重构方法
1.1 基于布里渊分布式光纤应变监测技术
为获取大型储液罐薄壳壁结构的应变数据,采用分布式光纤传感器进行应变数据采集,由分布式光纤应变测量原理[12],假设被测基体为薄壳壁截面弹性结构,被测基体发生机械纯弯曲变形。取长度为l0、厚度为h0的微元进行分析。当一对外加弯矩M作用在微元的纵向对称平面上时,微元发生塑性弯曲变形。变形区域存在一个长度保持不变的应变中性层o1~o2。微元弯曲内侧收缩,弯曲外侧伸长,长度变化量为Δl。若传感光纤通过胶剂粘贴在被测量面上(如图 1 所示),当被测表面发生变形时,对于粘贴在结构微元表面上的光纤微元来说,微元弯曲产生的应变通过粘贴层传递给传感光纤微元[13]。微元弯曲内侧的传感光纤被压缩,产生轴向压应变;微元弯曲外侧的传感光纤被拉伸,产生轴向拉应变。同应变变化前相比,局部光纤片段的瑞利光谱将分别在正负方向上发生偏移。通过检测光谱偏移量的方向,可以判断被测表面变形的方向;通过解调光谱偏移量的大小,可以获得微元在x或y方向上的应变。
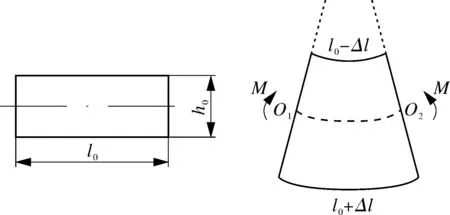
图1 微元的纯弯曲结构模型
根据图1所示,测量点位置处的变形和该位置处粘贴的局部传感光纤的瑞利光谱偏移量的关系可以表示为:
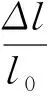
(1)
式中,Δl表示微元模型的长度变化量,mm;l0表示微元模型的长度,mm;K为表面形变测量的比例系数;Δλ为光波长偏移量。
在光纤分布式传感中,光纤片段作为传感单元,通过测量该片段的瑞利光谱的偏移量对应变进行解调,所以传感单元输出的是该传感单元长度范围内的平均应变。从被测表面到传感单元的平均应变传递系数为:
(2)
式中,L为传感单元长度;f,s分别为光纤、基体的基本物理参量;ε为轴向应变;dz为位移。
1.2 模态叠加法理论
对结构进行动力学分析可知,对于参数分布系统,理论上需要通过偏微分方程来描述其变形[14]。但实际上,可将储液罐罐体结构看成一个由外载荷P作用下的多自由度的有阻尼系统,整体结构有限元节点总数为N,在外载荷P作用下的变形位移y(t)可由如下运动方程来描述:
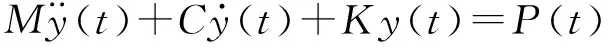
(3)
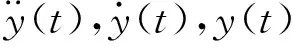
若忽略阻尼影响,假设系统的外载荷矢量P(t)=0,则系统的振型方程为:
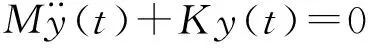
(4)
因此,对于线性系统,可以通过求解式(4)振型方程得到各阶特征方程:
(5)
式中,ωi为系统的第i阶固有频率,每一个固有频率ωi对应的自由振动幅值为Φi;{Φi}为薄壳壁结构的第i阶位移振型。
通过求解可以得到第i阶固有频率对应的自由振动幅值Φi:
(i=1,2,3,…,n) (6)
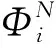
由模态叠加原理,储油罐薄壳壁结构的变形位移y(t)可以表示为:
(7)
式中,qj为系统运动的广义坐标,称为主坐标矩阵。
储液罐薄壳壁结构的位移模态表示为该结构的固有振型,应变是位移的一阶导数。因此,对于每一阶位移模态,必有其对应的固有应变分布,这种与位移模态相对应的固有应变分布状态称之为应变模态[15]。
ψi=D(φi)
(8)
式中,ψi为储液罐薄壳壁结构的第i阶应变模态;D为位移到应变的线性系统微分算子;φi为储液罐薄壳壁结构的第i阶位移模态。
由模态叠加原理[16],可得薄壳壁结构在载荷作用下的应变响应为:
(9)
式中,M为选取的应变点个数;{q}i为应变模态坐标。
由模态分析可以得出结构这M个点的应变振型矩阵[ψ]M×i,由布里渊分布式光纤传感器可以测得结构的应变响应{ε}M,在M≥i时可以求出模态坐标{q}i,即有:
(10)
在求得薄壳壁结构前i阶模态所对应的广义模态坐标{q}i,且在已知前i阶位移模态的条件下,则可以得到在受到不均匀沉降和地震等因素下储液罐薄壳壁结构精度的节点估计位移表达式为:
=[Φ]N×i{q}i
[S-D]M×i
(11)
式中,矩阵[S-D]M×i为应变-位移转换矩阵。
模态叠加变形算法的本质是通过应变位移转化矩阵,将测得的应变场转化为位移场[17]。因此,可简写为:
(12)
式中,N为储液罐薄壳壁结构位移计算节点总数。
2 试验与分析
2.1 储液罐试验平台构建
试验系统由布里渊光纤分析仪、储液罐薄壳壁板试验台、控制计算机组成,搭建储液罐应变监测系统试验平台如图2(a)所示。对于二维表面分布应变的测量,需要根据被测表面的形状和容易发生变形的区域,对传感光纤在被测表面分布的物理路径进行优化设计。储液罐薄壳壁板连接表面存在焊缝,结构表面不平整,有可能出现应力集中现象,使所测量的应变数据出现突变,因此,对储液罐试验台罐壁局部打磨,使所测量区域结构表面光滑,布设方式如图2(b)所示。

图2 储罐应变监测系统试验平台及布设方式

图3 储液罐薄壳壁结构载荷加载方式
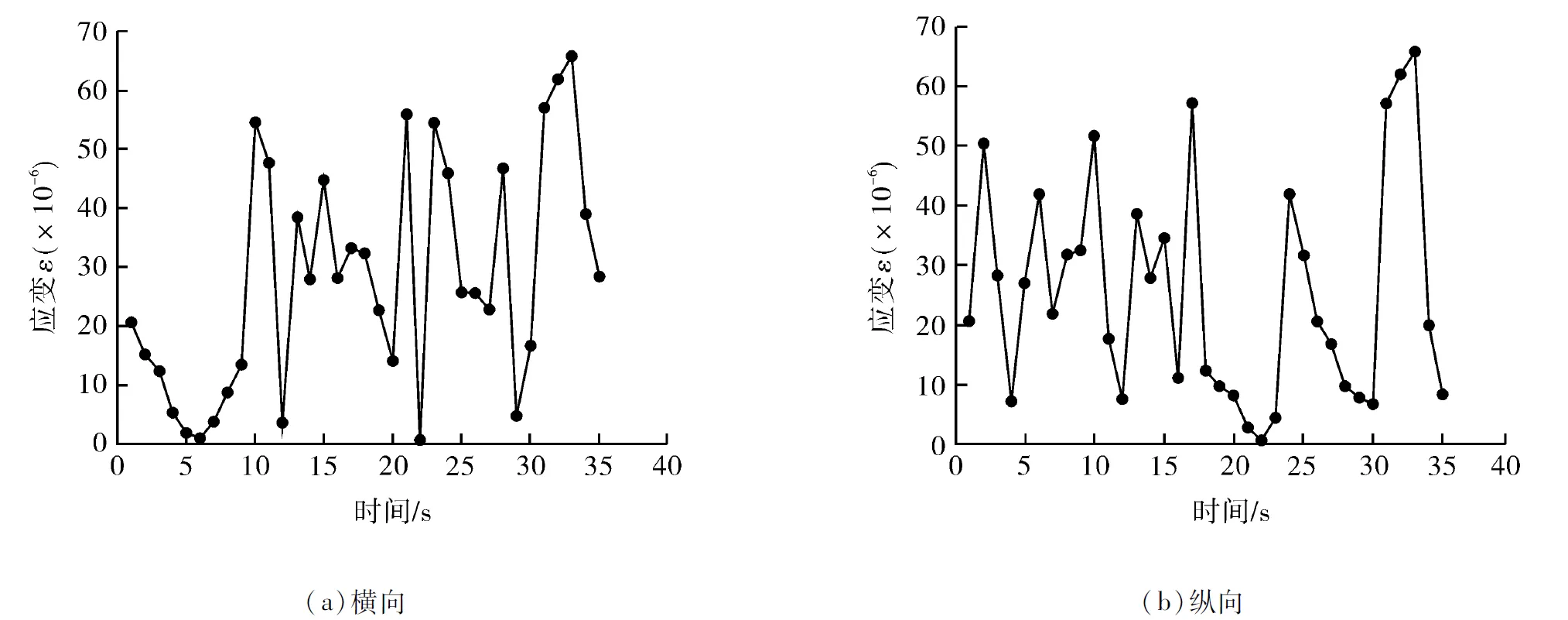
图4 不同载荷加载方向的应变-时间历程曲线
针对大型储液罐体积大、风险较高、发生事故后果严重等特点,实验室模拟现场监测方式,对简化的储液罐薄壳壁结构采用分布式光纤进行大范围整体监测,试验中使用了空间分辨率为1 m的商用光时域背向布里渊散射分布式光纤传感器(Brillouin Optical Time Domain Reflectometer,BOTDR)(横河AQ8603型)。采用等距取样的方式采集布里渊分布式光纤传感器所监测的应变数据,取样间隔为10 cm,取10 m长的光纤布设在薄壳壁结构上。同时在储液罐薄壳壁结构上加载横向载荷和纵向载荷,加载方式如图3所示。其中,横向加载载荷1 000 N,薄壳壁板的中心内部区域所受载荷作用最大,板的四周所受载荷作用最小;纵向加载载荷1 000 N,薄壳壁板的上边缘中心位置所受载荷作用最大,下边缘和板的两侧所受载荷作用最小。最后使用分布式光时域分析仪对应变数据进行采集,将得到的应变数据保存到控制电脑,使用Origin软件对数据进行整理,选取横向加载和纵向加载条件下的各35个数据,得到应变-时间历程曲线如图4所示。
2.2 有限元分析
为简化分析,将大型储液罐简化为一块薄壳壁结构[18],利用有限元分析软件建立薄壳壁几何模型。先对储液罐薄壁结构进行模态分析,再对薄壁结构进行静力学分析[19],获得在施加载荷作用下的薄壁结构的应变信息和变形位移信息,储液罐薄壁结构长1 200 mm,宽800 mm,厚6 mm,材料性能参数见表1。仿真结构模型见图5。
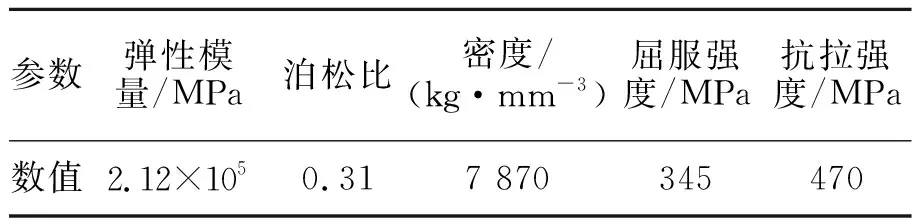
表1 储液罐薄壁结构材料Q235B性能参数
模态分析能够获得薄壳壁结构在不同固有频率下的受力情况以及形态特征,经研究发现,模态分析中低阶模态对结构的振动影响较大,高阶模态影响较小,且高阶模态很难精确计算。为了在保证精度的情况下,提高计算效率,只需要对低阶模态进行分析即可,因此只提取薄壳壁板前3阶模态,前3阶固有频率如表2所示,应变模态和位移模态如图6所示。
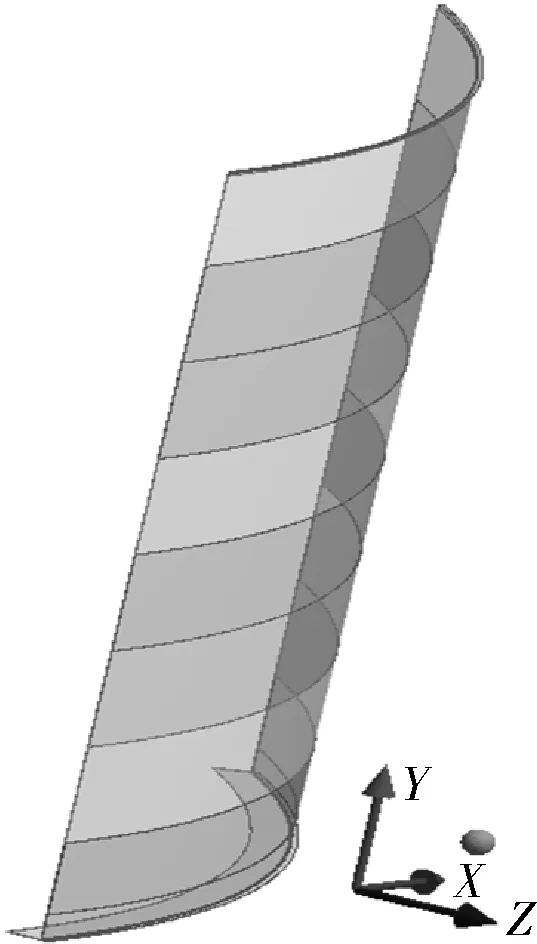
图5 储液罐薄壳壁结构有限元模型

表2 储液罐薄壳壁结构前3阶固有频率
在大型储液罐薄壳壁结构中,储液罐的不均匀沉降变形和屈曲变形对储液罐结构整体的共振效应起到关键作用[20-21]。由图6可看出,其薄壳壁结构前3阶模态固有频率较低,与储液罐设备在运行过程中的重要沉降频段比较靠近。本文主要进行薄壳壁板状结构受力集中部位加载载荷的变形监测,由此结构的响应主要由1阶模态控制。
为验证模态叠加变形重构算法的可行性和提高变形重构算法的精确度,对储液罐薄壳壁结构进行静应力分析,在该薄壳壁结构内壁施加Z方向的压力2.1 MPa,分别在Y轴反方向和Z轴正方向施加载荷大小为1 000 N的力,对该薄壁板底部施加固定约束,得到储液罐薄壁板应力分布云图和位移云图如图7所示。
3 试验结果分析
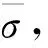

图6 应变模态和位移模态云图

图7 薄壁结构不同方向加载下的应变云图与变形位移云图
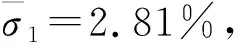
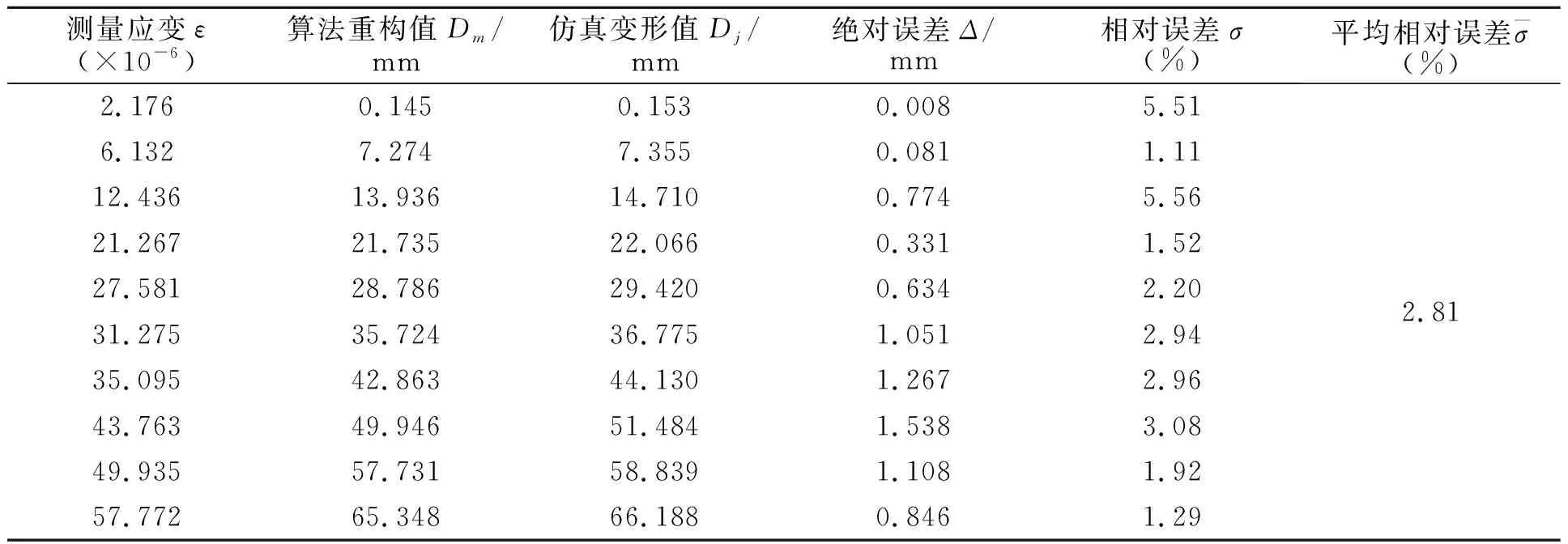
表3 横向(Y轴)加载载荷变形重构误差分析
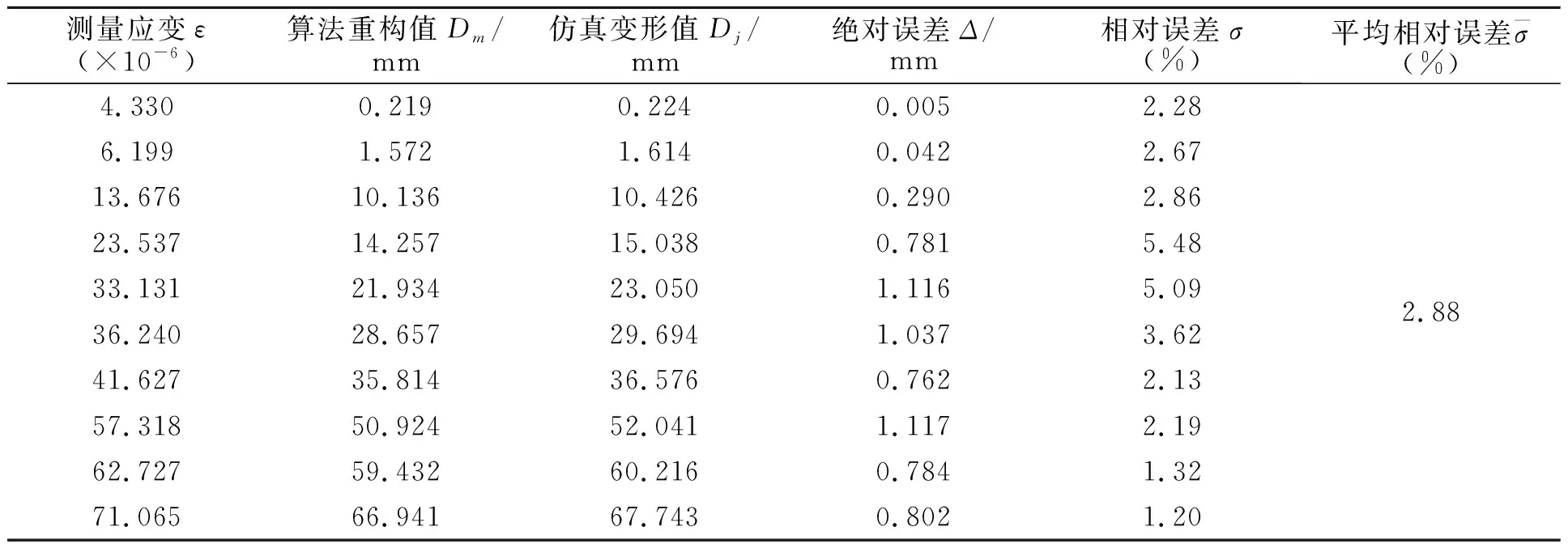
表4 纵向(Z轴)加载载荷变形重构误差分析
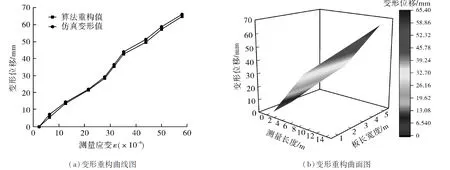
图8 横向载荷下的变形曲线图与曲面重构图
4 结论
(1)本文提出的模态叠加原理计算方法在实际测量中能呈现出较高的重构精度且精度产生的绝对误差最大为1.538 mm,相对误差最大为5.56%,平均相对误差小于3%。
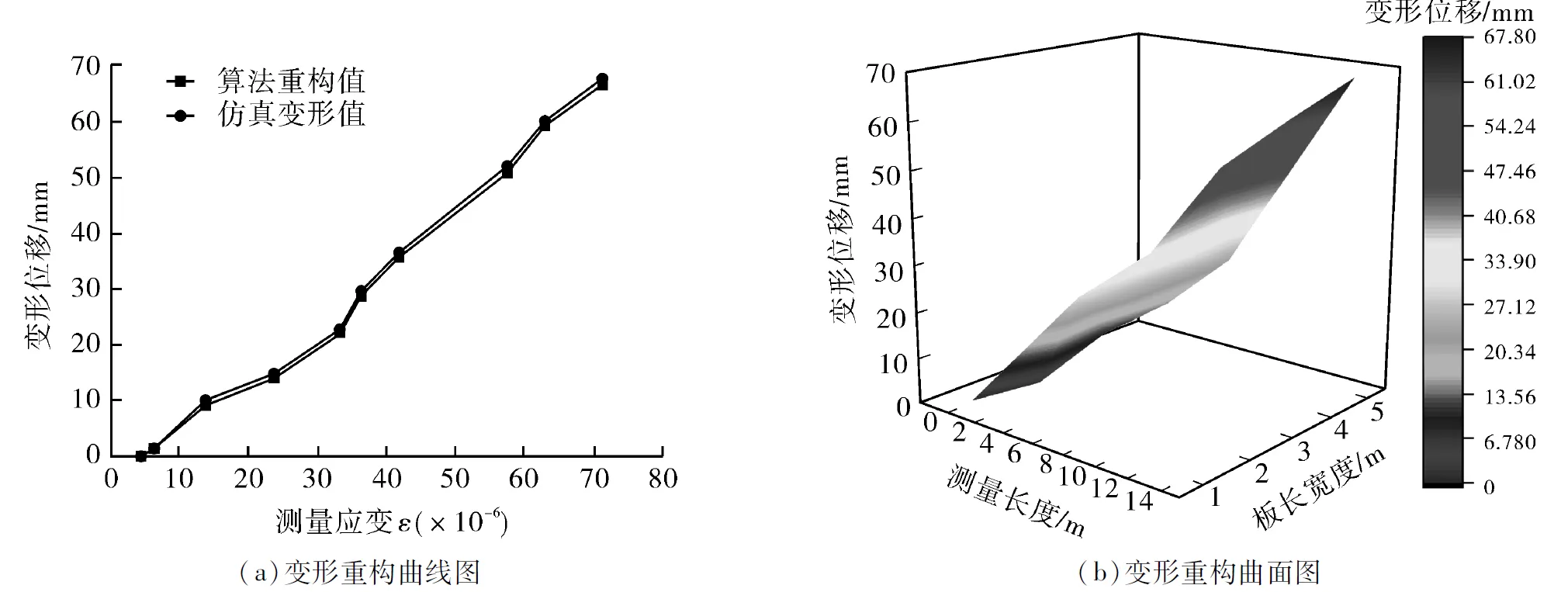
图9 纵向载荷下的变形曲线图与曲面重构图
(2)基于分布式光纤应变监测的模态叠加原理变形重构方法,可为大型储液罐薄壳壁结构的形状感知和健康监测提供一条新思路。
(3)验证了模态叠加原理变形重构计算方法不仅可用于航空领域,还可用于石化行业结构健康监测中,通过进一步研究可推广至在役大型储液罐的变形监测与评价中,具有一定的工程应用价值。

