综合CEEMDAN-SVD与倒频谱的滚动轴承故障诊断方法
郑锦妮,边 杰,2,3
(1.中国航空发动机集团 湖南动力机械研究所,湖南 株洲 412002;2.中国航空发动机集团 航空发动机振动 技术重点实验室,湖南 株洲 412002;3.直升机传动技术国防科技重点实验室,湖南 株洲 412002)
滚动轴承被广泛应用于各种旋转机械设备中,其运行状态的好坏关系到机械设备能否安全可靠工作。滚动轴承作为运动部件,容易发生故障。对滚动轴承进行状态监测与故障诊断,对于了解机械设备的运行状况和解决由轴承引起的各种机械设备的振动故障问题有着重要意义[1]。
滚动轴承发生故障时,会产生明显的调幅调频现象,这种调幅调频故障信号具有非线性、非平稳特征。因此,对滚动轴承故障信号进行准确解调是故障特征提取与诊断的前提[2]。对于具有非线性和非平稳特征的故障信号,传统的傅里叶变换不再适应,需使用自适应的信号分解方法对其进行解调。经验模态分解(empirical mode decomposition,EMD)是最常用的自适应的信号分解方法,被广泛用于机械故障诊断中,并取得了较好的诊断效果[3]。但是EMD方法在进行信号分解时存在模态混叠现象[4]。集合经验模态分解(ensemble EMD,EEMD)能在一定程度上改善模态混叠现象,但是其分解结果容易受到残余噪声的影响[5]。互补集合经验模态分解(complementary EEMD,CEEMD)对EEMD方法进行了改进,减小了EEMD方法残余噪声的影响[6]。但会导致运算翻倍,计算量大增[7]。针对EEMD方法和CEEMD方法的上述问题,自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)[8-10]被提出,该方法重构误差小,保证了其分解过程的完整性,同时克服了EEMD方法和CEEMD方法分解效率低下的问题。
作为一种非线性滤波方法,奇异值分解(singular value decomposition,SVD)以重构矩阵为基础,可以有效去除信号中的随机噪声,最大程度地保留有用信息,提高信噪比,使得故障信号中的故障特征能更加容易被提取出来。魏永合等[11]将EEMD与SVD用于齿轮故障诊断,结果表明该方法对复杂信号中的微弱故障特征信息具有较好的提取效果。马增强等[12]提出了VMD-SVD联合降噪与FSWT相结合的故障特征提取方法,表明该方法能有效消除噪声的影响,能较好地提取故障信号的故障特征频率。
倒频谱是指信号的对数功率谱的逆,与对数功率谱是一对傅里叶变换,由于其具有时间因次,也被称为时谱。倒频谱分析是一种二次分析技术,它受传感器测点位置以及传输路径的影响较小,能将原来频谱图中成簇的边频带谱线简化为单根谱线,便于观察。滚动轴承发生故障时,虽然SVD降噪可以有效去除滚动轴承故障信号中的随机噪声,但是经SVD降噪后的滚动轴承故障信号功率谱中,仍然存在着大量的非对称分布边频,给滚动轴承故障诊断带来困难。借助倒频谱则可将功率谱中成簇的边频带谱线化成单根的倒频谱线,由此可以检测出功率谱中难以辨识的周期性信号(故障特征频率)。罗毅等[13]提出了基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法,实现了齿轮裂纹故障的精确诊断。张博等[14]将倒频谱用于直驱风机主轴轴承的故障诊断中,有效地识别出轴承各频率成分的谐波周期和边频成分,辨识其故障位置。
本文将CEEMDAN方法融合SVD降噪并结合倒频谱分析,提出了一种综合CEEMDAN-SVD与倒频谱的滚动轴承故障诊断方法。该方法首先使用CEEMDAN方法实现对滚动轴承故障信号的自适应分解,然后利用相关系数判别准则,剔除与轴承故障信号相关性小即包含故障特征不明显的模态分量。为了消除分解得到的模态分量中的背景噪声以及CEEMDAN方法所添加的残余噪声对故障特征提取的影响,对上述模态分量进行SVD降噪,突出故障冲击特征,并对降噪后的模态分量进行倒频谱分析,以提取轴承故障特征频率,实现对轴承故障的有效诊断。
1 自适应噪声完备集合经验模态分解
自适应噪声完备集合经验模态分解(CEEMDAN)方法可在一定程度上克服EMD和EEMD方法中存在的模态混叠、残余噪声、附加模态以及计算量大等问题。在CEEMDAN方法中,在分解的各个阶段加入特定的噪声而非高斯白噪声。CEEMDAN方法不仅可以解决EEMD方法的问题,准确实现信号分解,并且其循环迭代时间也只有EEMD方法的一半。
为了更好地理解CEEMDAN算法,定义算子Ek(·)用于求解EMD分解的第k个模态分量IMFk,wi为服从N(0,1)分布的白噪声,εk为第k个阶段所添加的白噪声的幅值系数。CEEMDAN方法的分解过程如下[15]:
1) 在原始信号中添加白噪声X(t)+ε0wi(t),进行EMD分解,对分解结果进行平均得到IMF1:
(1)
2) 计算第一阶段的剩余分量:
r1(t)=X(t)-IMF1 .
(2)
将白噪声r1(t)+ε1E1(wi(t)),i=1,2,…,I加入第一阶段的剩余分量中,并进行EMD分解,则由第一个IMF的均值可以计算得到IMF2:
(3)
对于k=1,2,…,K,计算第k个剩余分量为
rk(t)=rk-1(t)-IMFk.
(4)
3) 将白噪声rk(t)+εkEk(wi(t)),i=1,2,…,I加入至第k个剩余分量,并进行EMD分解,则由第一个IMF的均值可以计算得到IMF(k+1):
(5)
4) 重复第2)和第3)步,直至剩余分量不能再进行EMD分解。最后,得到的剩余信号为:

(6)
其中,K为分解所得到的模态分量个数。
则,重构的信号可以表示为:
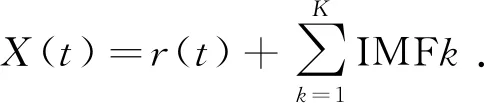
(7)
2 奇异值分解与倒频谱
奇异值分解(SVD)是一种分析矩阵的线性代数技术。式(7)中由CEEMDAN分解得到的第k个模态分量IMFk,在SVD中可以被分解成3个矩阵,其定义如下[16]:
IMFk=UΛVT.
(8)
其中,U和V为正交矩阵;Λ为对角矩阵,其对角线元素σi表示IMFk的奇异值。奇异值通过SVD函数自动按降序列出,
σ1(IMFk)≥σ2(IMFk)≥…≥σI(IMFk) ;
(9)
将SVD应用于第k个模态分量IMFk后,包含故障特征向量的IMFk的奇异值σ(IMFk)可由式(10)得到:
σ(IMFk)=[σ1(IMFk),σ2(IMFk), …,σI(IMFk)] .
(10)
倒频谱定义为信号的离散傅里叶变换(DFT)的对数幅值的离散傅里叶逆变换(IDFT).根据倒频谱定义的不同,其可以分为复倒频谱和实倒频谱。复倒频谱定义如下[17]:
cc(n)=F-1{lg[F{x(n)}]} .
(11)
实倒频谱最早用于工程中,其能捕捉到所感兴趣的信号的相关信息,实倒频谱的定义如下:
cr(n)=F-1{lg|F{x(n)}|} .
(12)
式中:x(n)为采集的信号,n为离散时间序号;F和F-1分别表示DFT和IDFT.
3 滚动轴承故障诊断
为了验证本文方法的有效性和实用性,使用本文方法对实测滚动轴承振动信号进行诊断分析。试验滚动轴承的型号为6205-2RS JEM SKF,滚动轴承尺寸见表1.使用电火花在试验滚动轴承上注入直径为0.177 8 mm、深0.279 4 mm的单点故障。试验滚动轴承的转速为1 725 r/min(转频为28.75 Hz),使用振动加速度传感器采集振动信号,采样频率12 kHz.由此,可计算滚动轴承内圈故障特征频率、外圈故障特征频率和滚动体故障特征频率分别为155.69 Hz,103.06 Hz和135.51 Hz.

表1 试验滚动轴承尺寸Table 1 Size of test rolling bearings mm
3.1 正常状态
采集在正常状态下滚动轴承振动信号的时域波形如图1(a)所示,正常滚动轴承振动信号的振动幅值较小,振动单峰值在0.15×9.8 m/s2左右。由于单从时域波形并不能判别滚动轴承的状态,需要对时域信号做进一步的处理分析。使用CEEMDAN方法对时域信号进行分解,并对分解结果进行SVD降噪,得到4个IMF分量和1个剩余信号,如图1(b)所示。对所得的4个IMF分量进行倒频谱分析,图1(c)为4个IMF分量的倒频谱。从图1(c)可以看出,IMF1~IMF4分量的倒频谱上具有以转频的倍频的倒数为周期的倒谐波,却没有以其他故障频率的倍频的倒数为周期的倒谐波,将这些倒频率转换为相应的频率即为转频的倍频。由于无其他故障特征频率存在,说明滚动轴承处于正常状态。
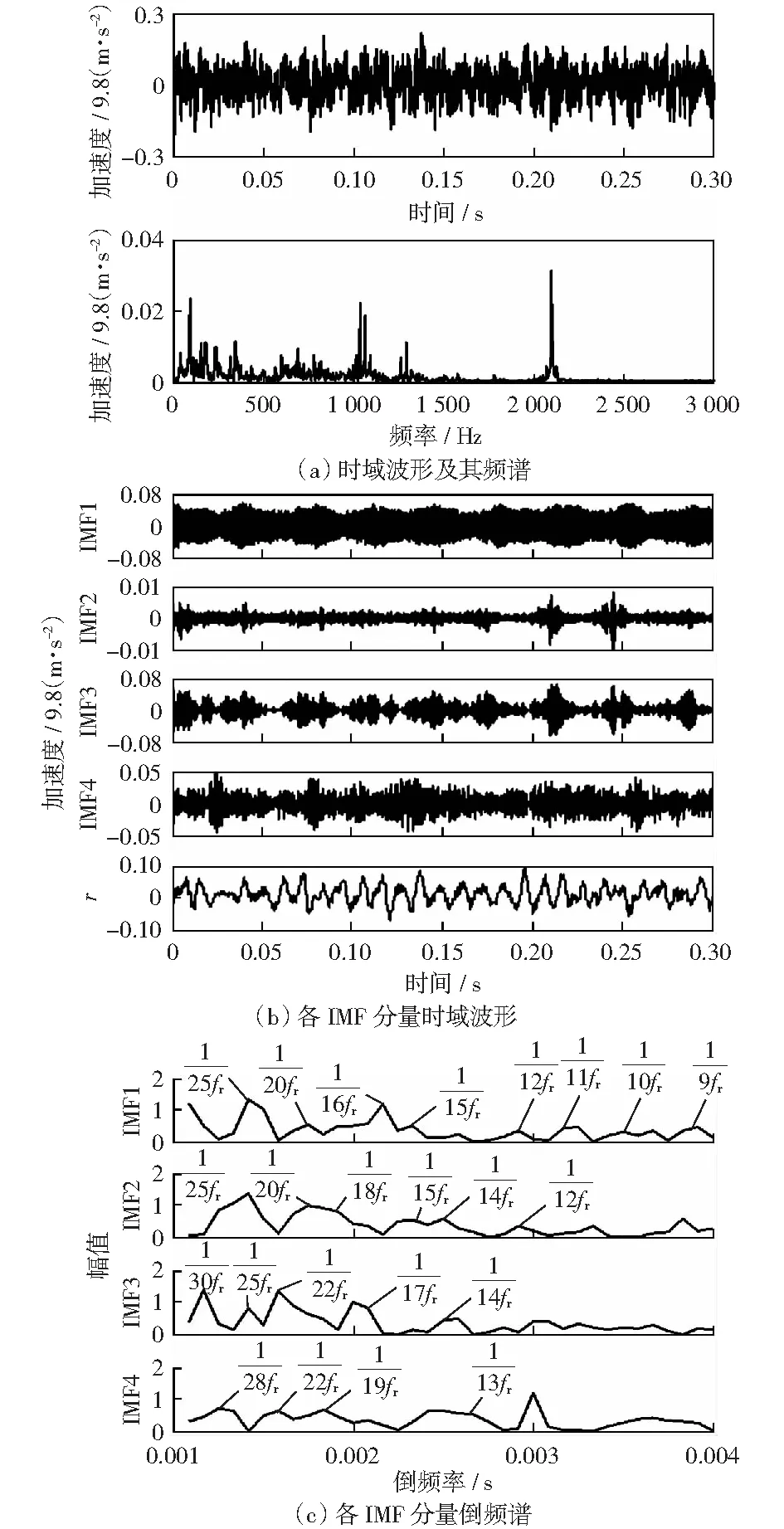
图1 正常滚动轴承振动信号及其CEEMDAN-SVD分解结果Fig.1 Vibration signal of normal rolling bearing and its decomposition results by CEEMDAN-SVD
3.2 内圈故障
滚动轴承内圈故障信号的时域波形见图2(a).与正常滚动轴承振动信号时域波形相比,滚动轴承内圈故障信号的时域波形幅值明显增大,振动单峰值达到1.5×9.8 m/s2左右,并且具有明显的周期性冲击特征,但仅从时域波形很难判断滚动轴承发生了何种故障。
对滚动轴承内圈故障信号进行CEEMDAN分解及SVD降噪处理,获得3个IMF分量和1个剩余信号,如图2(b)所示。图2(c)为3个IMF分量通过倒频谱变换得到的倒频谱图。从IMF1~IMF3分量的倒频谱图中,可以清晰地发现倒频谱上存在一些特定的倒谐波,将其周期转换过来的频率为滚动轴承内圈故障特征频率的倍频mfi、转频fr及其倍频mfr对滚动轴承内圈故障特征频率的倍频mfi的调制频率。这些频率的存在说明了滚动轴承的内圈发生了故障。与正常状态下滚动轴承振动信号IMF分量的倒频谱只包含转频的倍频mfr谱线不同,滚动轴承内圈故障信号IMF分量的倒频谱主要包含滚动轴承内圈故障特征频率的倍频mfi谱线和转频fr及其倍频mfr对mfi的调制频率谱线。
3.3 外圈故障
滚动轴承外圈故障信号的时域波形如图3(a)所示,与正常滚动轴承振动信号时域波形相比,其振动幅值增大更加明显,振动单峰值达到3.0×9.8 m/s2.同样,其时域波形存在典型的周期性冲击特征,单从图3(a)中的时域波形很难看出引起滚动轴承冲击脉冲的具体损伤部位,即无法准确对滚动轴承进行故障诊断。
如图3(b)所示,使用CEEMDAN方法将该时域信号分解成2个IMF分量和1个剩余信号,并对所得的IMF分量进行SVD降噪。然后对SVD降噪后的2个IMF分量进行倒频谱分析,其结果如图3(c)所示。在IMF1和IMF2分量中,存在一些明显的倒谐波,将其周期转换为相应的频率后,发现这些倒谐波的频率对应为滚动轴承外圈故障特征频率的倍频mfo、转频fr及其倍频mfr对滚动轴承外圈故障特征频率的倍频mfo的调制频率。这些频率的存在说明了滚动轴承的外圈发生了故障。同样,与正常状态下滚动轴承振动信号IMF分量的倒频谱只包含转频的倍频mfr谱线不同,滚动轴承外圈故障信号IMF分量的倒频谱主要包含滚动轴承外圈故障特征频率的倍频mfo谱线和转频fr及其倍频mfr对mfo的调制频率谱线。
3.4 滚动体故障
滚动轴承滚动体故障信号的时域波形如图4(a)所示,与正常滚动轴承振动信号时域波形相比,其振动幅值稍微增大,振动单峰值达到0.30×9.8 m/s2.同时,其时域波形存在较明显的周期性冲击特征,但是仅从图4(a)中的时域波形不能判断引起滚动轴承冲击脉冲的具体损伤部位,即无法对滚动轴承故障进行准确诊断。

图4 滚动轴承滚动体故障信号及其CEEMDAN-SVD分解结果Fig.4 Fault signal of rolling bearing ball and its decomposition results by CEEMDAN-SVD
如图4(b)所示,使用CEEMDAN方法将该时域信号分解成3个IMF分量和1个剩余信号,并对所得的IMF分量进行SVD降噪。然后对SVD降噪后的3个IMF分量进行倒频谱分析,其结果如图4(c)所示。在IMF1~IMF3分量中,存在一些明显的倒谐波,将它们的周期转换为相应的频率后,发现这些倒谐波的频率对应为滚动轴承滚动体故障特征频率的倍频mfb、转频fr及其倍频mfr对滚动轴承滚动体故障特征频率的倍频mfb的调制频率。这些频率的存在说明了滚动轴承的滚动体发生了故障。与正常状态下滚动轴承振动信号IMF分量的倒频谱只包含转频的倍频mfr谱线不同,滚动轴承滚动体故障信号IMF分量的倒频谱主要包含滚动轴承滚动体故障特征频率的倍频mfb谱线和转频fr及其倍频mfr对mfb的调制频率谱线。
4 结论
使用CEEMDAN方法对正常状态、内圈故障、外圈故障和滚动体故障4种状态下的滚动轴承振动信号进行分解,然后对分解结果进行SVD降噪,并对SVD降噪后的IMF分量进行倒频谱分析,得到结论如下:
1) 正常状态下滚动轴承振动信号IMF分量的倒频谱只包含转频的倍频mfr谱线,而不存在其他故障特征频率谱线。
2) 滚动轴承内圈故障信号IMF分量的倒频谱主要包含滚动轴承内圈故障特征频率的倍频mfi谱线和转频fr及其倍频mfr对mfi的调制频率谱线。滚动轴承内圈故障特征频率fi的谐波频率及其调制频率谱线的存在,可以确定滚动轴承内圈故障的发生。
3) 滚动轴承外圈故障信号IMF分量的倒频谱主要包含滚动轴承外圈故障特征频率的倍频mfo谱线和转频fr及其倍频mfr对mfo的调制频率谱线。滚动轴承外圈故障特征频率fo的谐波频率及其调制频率谱线的存在,可以确定滚动轴承外圈故障的发生。
4) 滚动轴承滚动体故障信号IMF分量的倒频谱主要包含滚动轴承滚动体故障特征频率的倍频mfb谱线和转频fr及其倍频mfr对mfb的调制频率谱线。滚动轴承滚动体故障特征频率fb的谐波频率及其调制频率谱线的存在,可以确定滚动轴承滚动体故障的发生。
5) 综合CEEMDAN-SVD与倒频谱的滚动轴承故障诊断方法,可以实现对滚动轴承振动信号的正确分解,从SVD降噪后的IMF分量的倒频谱中可以准确找到滚动轴承不同状态(正常状态、内圈故障、外圈故障和滚动体故障)时的特征频率,从而实现了对滚动轴承故障的有效诊断。

