基于数学素养发展的初中数学活动课研究——以人教版八下《二次根式的数学活动》为例

陈 漫

(广东省广州市南国学校 广东 广州 510000)

1.引言

“综合与实践”是《义务教育数学课程标准(2011)年版》(以下简称《课标》)重要的知识领域，凸显学生综合运用数学知识和数学思想方法解决实际问题的特点，有助于学生数学活动经验的积累与数学应用意识、问题解决能力等的培养。正如《课标》中指出的：“综合与实践旨在培养学生综合运用有关的知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累学生的活动经验，提高学生解决现实问题的能力，从而提高学生的数学素养。”[2]

人教版数学教科书中每个单元最后都安排有数学活动内容，其中八年级下册第十六章二次根式后设置了一个数学活动：做一个长方体纸盒。笔者现以“做一个长方体纸盒”这一数学活动为例，谈谈组织和实施数学活动的一些做法及思考，与同行们交流，权当抛砖引玉。

2.教材分析

本节课是人教版八年级下册第16章二次根式数学活动，让学生做一个长方体纸盒，这个纸盒的长、宽、高都是无理数，使学生感受二次根式在生产、生活实践中的应用。

3.学生分析

学生通过前面的学习，掌握了二次根式加减乘除运算的法则，能根据题意完成二次根式的基本运算。对于怎样画出长度为根号3的线段，在七下《实数》一章中提到有理数夹逼方法估算。同时，八年级的学生具有强烈的好奇心和求知欲，有一定的独立思考、实践操作、合作交流、归纳概括能力。

4.教材过程

4.1 引入。日常生活中，我们经常要用到各式各样的纸盒，牙膏盒、蛋糕盒、首饰盒等等，你会制作吗？

4.2 活动探究：制作长方体纸盒。

问题1：一个底面积为32cm2，长、宽、高的比为4:2:1的长方体，这个长方体的长、宽、高分别是多少？

小结：这个长宽高的形式都是有理数。

(过渡语)如果我把底面积改成24cm2，那长、宽、高分别是多少呢？

问题2：做一个底面积为24cm2，长、宽、高的比为4:2:1的长方体，这个长方体的长、宽、高分别是多少？

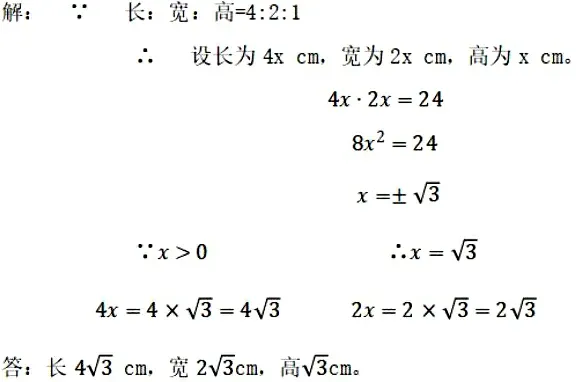
问题3：长方体的表面积是多少？

问题4：长方体的体积是多少？

问题5：如何做这个长cm,宽高cm

追问1：是多大呢？

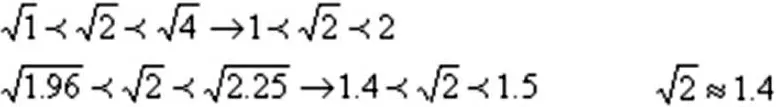
类似地，我们可以得到：

2、制作纸盒一般四个步骤：

①画：画平面展开图

②剪：用剪刀剪出长方体平面展开图

③折：将平面图中长方体内部的棱折出折痕

④粘：沿着折痕组合成长方体，在某些棱与棱的连接处用透明胶粘好

4.3 拓展延伸。学校准备修建一个底面积为16m2，高为1m的花坛，现有两种设计方案，底面建成正方形或者圆形，现将侧面铺上瓷砖，从节省材料的角度考虑，你选择哪种形状设计？请说明理由。请说明理由。

引导学生分析：怎样才是节省材料，要求什么？

节省材料→侧面积较小→底面周长×高→高一样，周长较小

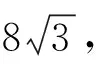
5.设计立意

环节一通过生活中熟悉的不同形状的纸盒入手，贴近生活。从实物中抽象出几何体，体会数学建模思想。

环节三拓展变式，结合具体背景的题目，从长方体拓展到其他形状——圆柱，让学生体会如何用数学知识解决实际问题。

6.教学反思

本节课是属于数学活动课，在整节课的实际操作中，要注重让学生动起手来，在做中学。教学过程中充分发挥学生的主观能动性，让他们独立思考，独立设计，独立制作，活动总结注意引导学生体会所学的数学知识在这个活动中的作用，引导他们去发现现实中的问题，并运用所学的知识加以解决，增强学生应用数学的意识。