基于自适应校正的动态直方图均衡算法
杨嘉能,李 华,田宸玮,钱育蓉
(新疆大学 软件学院,新疆 乌鲁木齐 830046)
0 引 言
直方图均衡化因其简单而有效被广泛应用于众多领域,是最常用的对比度增强方法之一。但它也存在一些缺点,主要为:灰度级的过度拉伸而导致的过增强和伪影;灰度级合并,细节信息丢失;平均亮度定向迁移。
近5年内有很多研究人员致力于直方图均衡算法的改进工作[1]。针对过度增强问题,MMSICHE[2]和BPCLBHE[3]通过直方图裁剪技术来抑制过增强现象。针对细节信息丢失问题,CLAHE[4]和QHELC[5]分别采用了gamma校正和直方图裁剪后再分配的方法来处理全局直方图,均有一定程度上的改善。针对亮度均值定向迁移问题,出现了基于保持亮度的BHE2PL[6]和BHE3PL[7]等改进算法,但不适用于低照度和高亮图像。因此,也有学者提出了动态直方图均衡化的概念用于增强过暗或过亮的图像,其代表算法有MEMBHE[8]、TDCHE-M[9]和QDHE[10]。
虽然有各种各样的技术来解决对比度增强的具体问题,但对低照度图像增强的探索仍显不足。R_ESIHE[11]和RS_ESIHE[11]都是针对低照度图像提出的增强算法,但由于采用了基于曝光值来分割直方图的方法,在处理亮度较低且全局直方图分布较窄的图像时会出现分割失败的情况,导致增强效果较差。因此本文在对现有的动态直方图均衡算法和低照度图像直方图的分布特性进行深入研究后提出了一种自适应的校正方法,其中包含亮度校正和对比度校正,在保留细节信息和抑制过度增强的同时达到合理的对比度增强。
1 直方图均衡算法的原理和关键
直方图均衡化的主要思想是基于其概率密度函数(probability density function,PDF)的均匀扩展来重新映射输入图像中每个像素的灰度级。其转换公式主要由映射区间和映射函数即累积分布函数(cumulative distribution function,CDF)构成。
直方图的PDF和CDF分别对应式(1)和式(2)
(1)
(2)
其中,q表示直方图上的某一灰度级,nq表示q灰度级上统计像素的个数,N表示输入图像的总像素,start表示某区间的最小灰度级。
根据式(2)得出直方图均衡化的转换公式为
F(q)=start+(end-start)×CDF(q)
(3)
其中,end-start表示映射区间。
分析式(3)可得,直方图均衡算法的关键在于映射区间的选取和CDF的构造。合理的映射区间和恰当的CDF能使获得的输出图像具有良好的亮度信息和丰富的细节信息,并且对比度可得到适中的增强。因此,如何根据输入图像的直方图的分布特性选取映射区间和构造CDF是此类算法的关键所在。
2 基于自适应校正的动态直方图均衡算法
本文所提出的基于自适应校正的动态直方图均衡算法(adaptive correction based dynamic histogram equalization,ACDHE)属于动态直方图均衡化技术,其中包含了自适应的亮度校正和自适应的对比度校正,下面将做详细介绍。
2.1 自适应的亮度校正
由于低照度图像的直方图往往分布在最左侧,动态范围较小,视觉效果昏暗,故需要进行亮度校正。考虑到传统的直方图均衡化存在亮度均值定向迁移的问题,故本文提出一种亮度校正方法。依据平均亮度值在全局直方图分布范围中的位置计算分割点,将全局直方图分割成两个子直方图,然后根据每个子直方图的分布范围来重新分配一个新的映射区间,达到亮度校正的效果。具体过程如下:
(1)计算全局直方图的分布范围
传统意义上,直方图的分布范围[Start,End]定义为
(4)
其中,h表示某个直方图,min()和max()分别是求取nq>0中q的最小值和最大值的函数,L表示输入图像总的灰度级数。
由于低照度图像中存在一些干扰噪声,会影响分布范围的计算,故本文提出了一种优化后的分布范围计算方式,能更有利于后续的直方图分割和重新分配映射区间,达到校正亮度的目的。计算公式如下
(5)
其中,m是一个设定的值,用于去除干扰噪声。
(2)计算全局直方图的分割点
传统的直方图分割技术有直接采用亮度均值[3,6]或累积像素中值所在点[10]的分割方式,也有两者结合[2]的分割方式,但此类方法都没有考虑直方图的特性,如分布范围、局部峰值等。有学者提出了基于局部峰的分割方式[12],但由于局部峰的搜索范围相对于直方图分布较窄且多为单峰的低照度图像来说并不适合,因此本文在亮度均值的基础上考虑了直方图的分布范围,提出了一种分割方式,即依据平均亮度值在全局直方图分布范围中的位置计算分割点,得到左右两个子直方图。计算公式如下
(6)
SP=len×(1-l)+Start
(7)
其中,l表示亮度均值在分布范围中的位置,len表示全局直方图分布范围的区间长度,range表示全局直方图的分布范围,SP表示分割点。
改进的分割方式能更好分离低照度图像直方图中的较大值与较小值,在校正亮度信息的同时改善了后续均衡化操作带来的灰度级合并的问题,减少细节信息的丢失。
(3)重新分配映射区间
为了确保每个子直方图得到合理的拉伸空间,需要对子直方图的映射区间进行重分配,以获得合理的亮度校正和对比度增强。本文依据子直方图在全局直方图中的分布占比来进行映射区间的重分配。该方法不同于QDHE的分配方法,不需要计算子直方图中像素的总量,因此计算简单,并且有效。映射区间分割点的公式如下
(8)
其中,MP表示映射区间分割点,SP-Start表示左直方图的分布范围。
m的取值决定了range的范围,同时也影响SP和MP的计算,从而最终影响映射区间的重分配,达到不同程度的亮度校正。本文采用亮度均值(mean brightness,MB)来衡量亮度校正的效果。图1展示了不同m值下的亮度校正结果以及与RS_ESIHE的对比,并且表1给出了其相关变量的值。亮度校正性能测试采用相同的CDF构造方法。
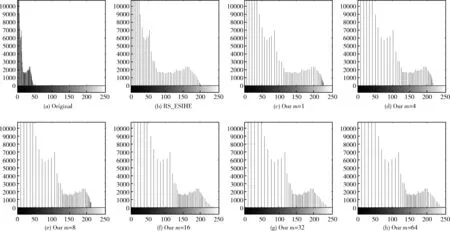
图1 不同阈值下的亮度校正对比结果
由图1(b)和图1(c)可以看出,在传统的直方图分布范围定义上,本文所提出的改进的直方图分割方法优于RS_ESIHE的基于曝光值的分割方法,亮度提升更明显。表1的MB值也验证了这一结果,而且从表1的SP值可以看出,基于曝光值的分割方法出现了分割失败的情况。由图1(c)至图1(h)可以看出,随着m的增大,亮度校正的效果越明显,且拉伸后的直方图分布范围更广,这表明本文所提出的改进的分割方法和映射区间重分配方法是有效的。但由表1的MB值和range可以看出,当m增大到一定程度时,随着直方图分布范围的稳定化,亮度校正的改善率会随之下降。
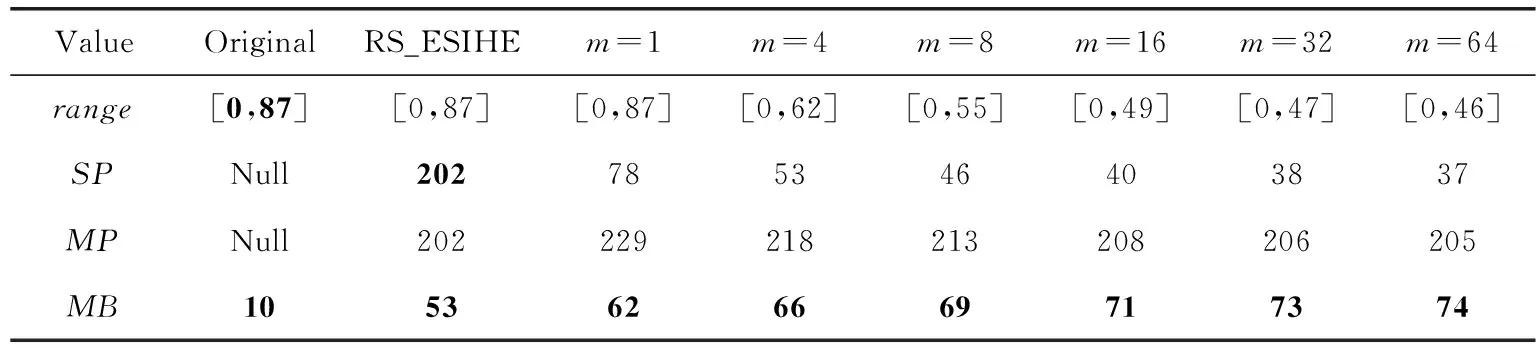
表1 不同阈值下的数据对比
2.2 自适应的对比度校正
低照度图像的像素在直方图中分布往往过于集中,导致所呈现的全局直方图容易出现尖峰状,从而引发过增强现象和细节信息丢失,故在增强时需要进行对比度校正处理。由于直方图均衡化的映射函数是CDF,故对比度增强率与其导数成正比,导函数如下
(9)
如果想要控制增强率,必须对PDF进行校正,或者直接校正直方图本身。本文提出一种自适应的对比度校正方法,即先通过直方图裁剪技术来校正直方图中的较大值,然后对超出阈值部分的像素进行数量上的调整后重新分配给直方图中的较小值,最终达到校正直方图的目的,控制增强率,保留细节信息。直方图校正过程如图2所示,具体如下:
(1)分别为左右两个子直方图计算裁剪阈值,公式如下
(10)
其中,Ti是子直方图的裁剪阈值,Ni是子直方图的像素总量,leni是子直方图分布范围的区间长度。裁剪阈值计算如图2(a)所示。

图2 直方图校正过程
(2)对超出裁剪阈值部分的像素进行数量上的统计,由比例系数α进行调整,公式如下
(11)
(12)
其中,Mi是子直方图中超出阈值部分的像素总量,rangei是子直方图的分布范围,ANi是对子直方图中较小值的调整量,α是比例系数。调整量计算如图2(b)所示,其中α值为1。
(3)用Ti和ANi对子直方图进行校正,校正公式如下
(13)
其中,na(q)是校正后的子直方图,如图2(c)所示。
裁剪阈值限制了直方图中的较大值,防止某些灰度级的过度拉伸;调整量增加了原直方图中较小值所占的比例,一定程度上防止了灰度级的合并和细节信息丢失,同时也起到调整对比度的作用。图3为我们的方法在不同α值下,即不同的调整量下的增强结果,其中m统一设置为16,并用对比度和信息熵作为客观评价指标。图4展示了α从0至1的过程中信息熵和对比度的变化过程。
从图3(b)至图3(e)可以看出,随着α值的增大,图像的亮度和对比度随之下降,呈现出不同的视觉效果,其中图3(c)有最好的视觉效果,细节信息丰富。从图4可以看出,当α值为零时有最大的对比度,并且对比度会随着α值的提升而下降;从信息熵来看,当α为零即调整量AN为零时,信息熵明显低于其它值,并随着α值的提升,信息熵会有一个先上升后下降的过程。通过调整α值能得到不同程度的对比度提升和细节信息的保留。
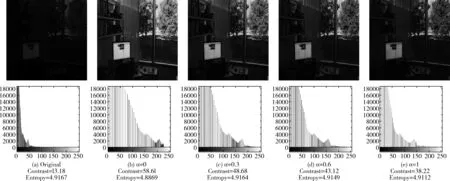
图3 不同比例系数下的增强结果
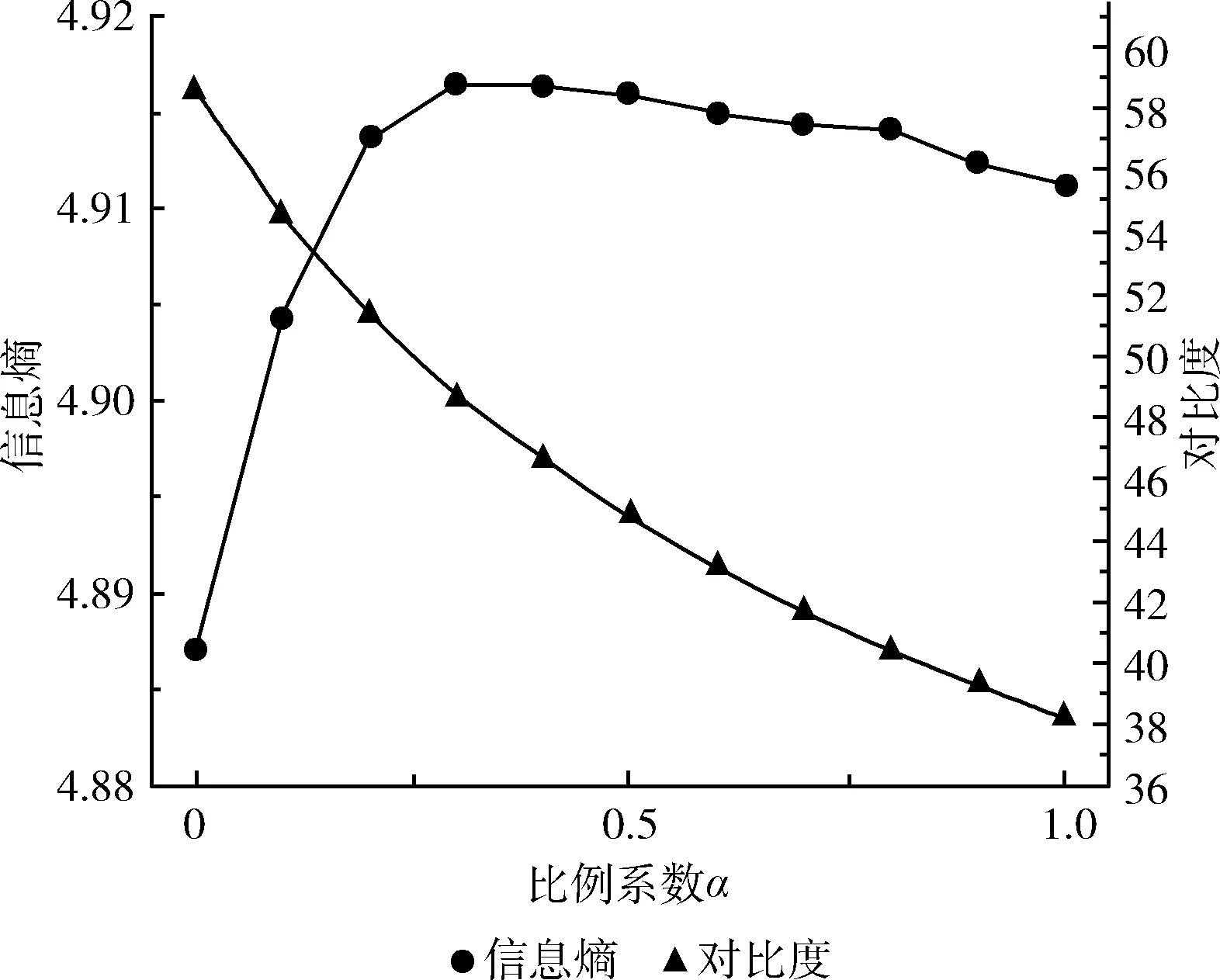
图4 不同比例系数下的对比度和信息熵
2.3 改进的动态直方图均衡
上两小节分别介绍了自适应的亮度校正和对比度校正,本小节将介绍本文ACDHE算法的步骤。具体如下:
ACDHE算法
输入:低照度图像
输出:低照度图像的增强结果
(1)Begin
(2)获得低照度图像的直方图n(q);
(3)用阈值m计算全局直方图的分布范围,获得分布区间range;
(4)用亮度均值在range中的位置计算分割点SP,将全局直方图划分成左右两个子直方图;
(5)依据子直方图的分布区间长度重新分配映射区间,或得映射区间分割点MP;
(6)计算裁剪阈值Ti;
(7)统计超出裁剪阈值的像素总量Mi,用比例系数α计算调整量ANi;
(8)对左右两个直方图进行校正,构造CDFi;
(9)分别进行均衡化处理,得到最终的增强结果;
(10)End
3 实验结果分析
为了验证本文算法的性能,采用了多个数据集进行测试,分别包括LOL[13]、SICE[14]、LIME[15],且这3个数据集都是作者在不同的真实场景下获取的低照度图像。为了进一步验证,本文选取MMSICHE、QDHE、TDCHE-M和RS_ESIHE作为对比算法,并对实验结果进行了主观和客观上的评价与分析。最后,在LOL数据集上进行了算法平均性能的比较,且对参数m和α的选取进行了讨论。
3.1 主观评价与分析
本文分别从3个数据集中各挑选了一张图像进行增强效果对比实验,如图5~图7所示,包含了室内、室外、远景,以及阴天、午夜和背光的低照度图像。实验中m选取的值为32,α选取的值为0.1。
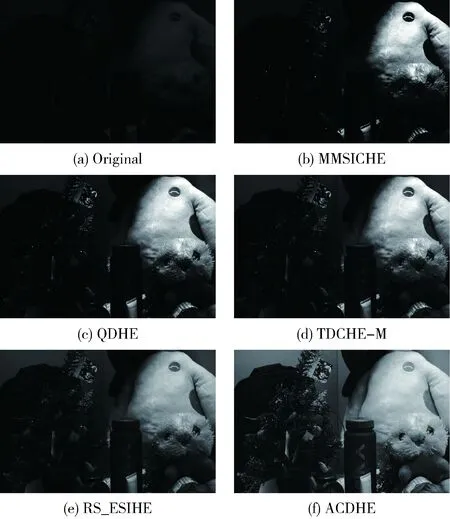
图5 室内图像的增强结果

图6 室外图像的增强结果

图7 远景图像的增强结果
从对比实验中可以看出,整体上ACDHE的增强结果不仅可以得到合理的亮度提升,且同时具有适当的对比度,相比于其它对比算法视觉效果更好。MMSICHE虽然采用了平均亮度和中值相结合的分割方式,但由于其保持亮度的特性,导致增强结果出现部分过暗和部分过亮的情况,因此增强结果不自然。QDHE和TDCHE-M和本文的方法一样,同属于动态直方图技术,且两者的增强结果较为相似,但由于其映射区间重分配方式的缺陷,仍存在亮度过低局部过暗的情况。RS_ESIHE的增强结果与我们的增强结果最为相似,但由于其分割方式存在的缺陷,图5和图6都出现了分割失败的情况,导致增强结果的对比度较低,整体亮度不够。针对图像细节部分,可以从图5的毛绒玩具和图7的月亮明显看出,本文的增强结果具有更丰富的细节信息,因此在细节保持能力上ACDHE算法优于其它对比算法。
3.2 客观评价与分析
本文采用了平均亮度、灰度级数、信息熵和对比度4个客观评价指标来衡量各个算法的性能。平均亮度代表了图像的亮度信息,灰度级数和信息熵代表了图像信息的丰富程度,对比度可用来衡量增强后的对比度提升情况,但不是越大越好。表2~表4给出了各个评价指标的结果。
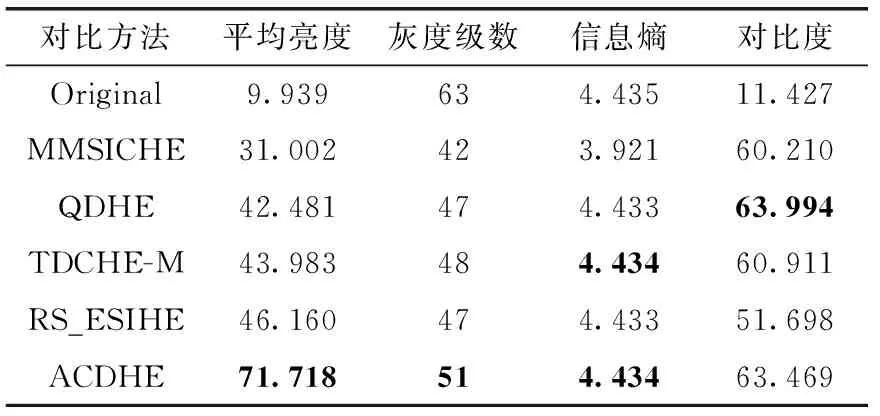
表2 图5增强结果的客观评价
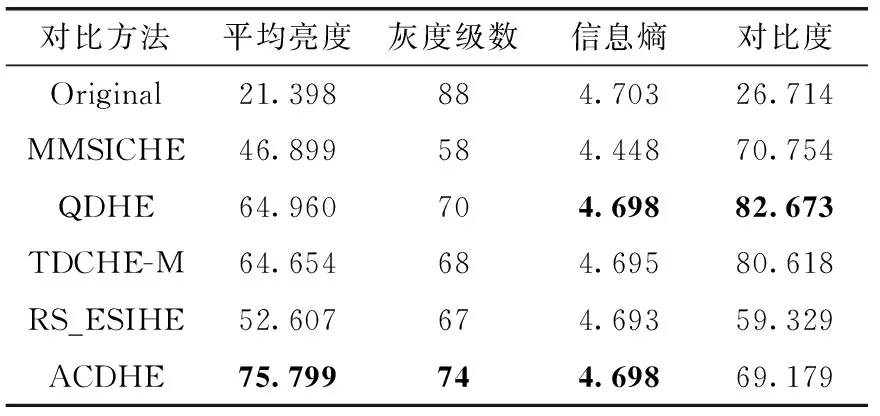
表3 图6增强结果的客观评价
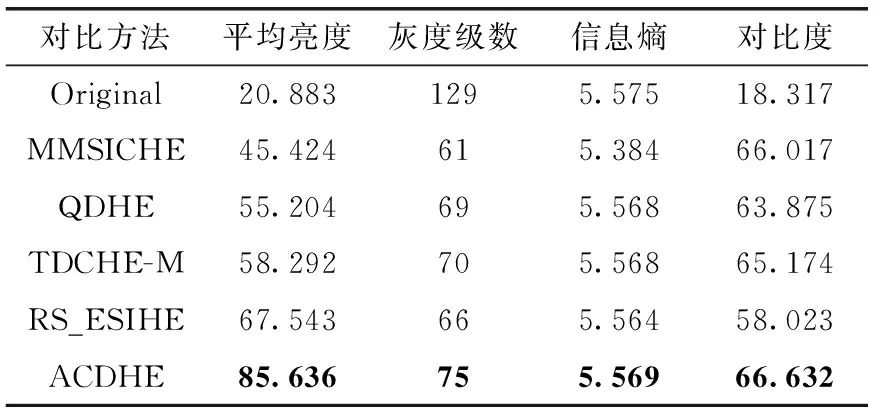
表4 图7增强结果的客观评价
表2~表4中对比算法评价指标的最优结果已加粗,且从表中可以明显看出,原始图像拥有最大的灰度级数和信息熵,但平均亮度和对比度非常低。ACDHE算法的平均亮度明显高于其它对比算法,且不存在平均亮度定向变化的问题,这意味着我们所提出的映射区间的重分配方法是有效的,原始图像的亮度得到了很好的校正。从灰度级数和信息熵可以看出,ACDHE算法保留了最多的灰度级,并且拥有最大的信息熵,非常接近原始图像。当然QDHE、TDCHE-M和RS_ESIHE的信息熵也很高,但本文的方法总能产生最大的信息熵。这意味着我们提出的调整量AN在防止灰度级合并和保留细节信息上起到了很好的效果,同时过度增强也得到了有效抑制。与此对应,ACDHE算法的对比度比较适中,反之QDHE和TDCHE-M的对比度不太稳定。因此从客观评价指标看,本文的算法在调整亮度、保留细节信息和控制对比度这几个方面优于其它对比算法。
3.3 算法平均性能和参数讨论
本小节将给出对比算法在LOL数据集上的平均性能,还对参数m和α值的选取进行了分析与讨论。LOL数据集包含485张图像,针对同一场景存在不同程度的低照度图像,且每一张低照度图像都有其正常光照下的参考图像。我们将增强结果与参考图像做客观评价对比,其中包含绝对平均亮度误差(absolute mean brightness error,AMBE)、峰值信噪比(peak signal-to-noise ratio,PSNR)和结构相似度(structural similarity,SSIM)。由于篇幅有限,表5给出了部分有代表性的参数值下的实验结果,关键数据已加粗。
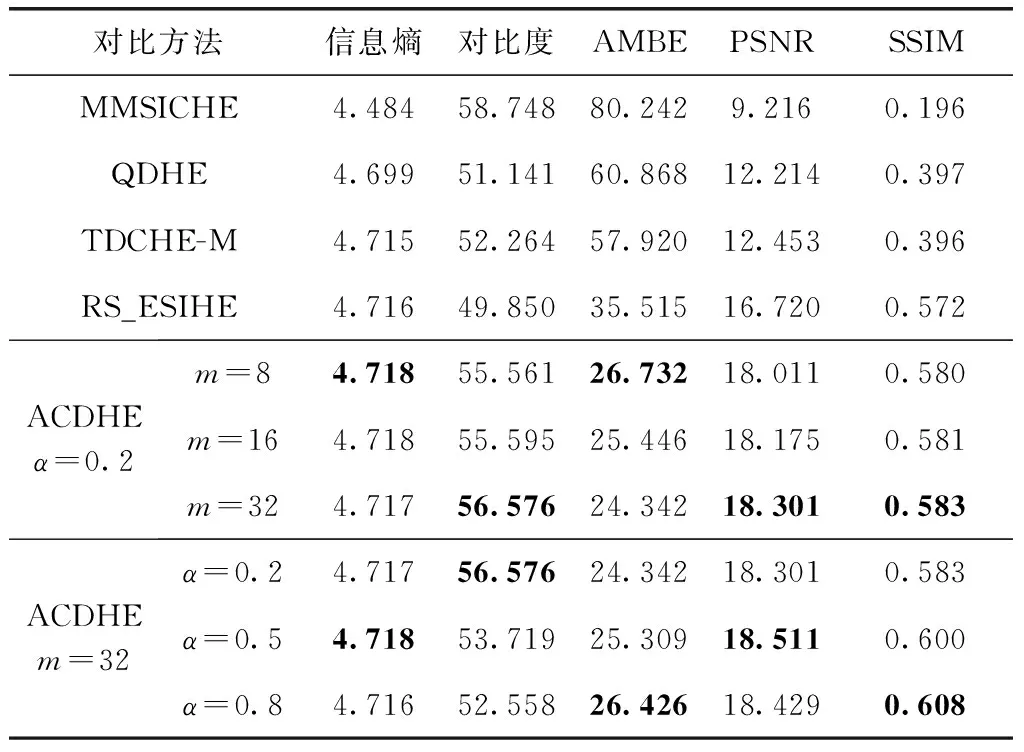
表5 算法平均性能的客观评价
从表5可以看出ACDHE算法在不同的参数选取下的平均性能都优于其它对比算法,不仅有最高的平均信息熵和很好的对比度,与正常光照下的参考图像有最小的平均亮度误差、最高的峰值信噪比和最好的结构相似性。这表明ACDHE算法的增强结果与参考图像最为接近,增强效果最好。
由参数的对比实验可以看出,当α值不变,m值增大时,增强图像的平均信息熵会有所下降,平均对比度有小幅提升,整体与参考图像会有更高的相似性。当m值不变,α值增大时,平均信息熵会先增大后减小,平均对比度会下降,与参考图像的整体相似性也会先增大后减小。由大量实验得出,对于噪声明显的低照度图像,可适当增加m的值以获取合理的重映射区间,在本文选取的数据集中,m值为32时,对于绝大部分图像会有较好的结果。针对控制对比度的参数α,当待增强图像的平均亮度小于20时,α取值为0~0.2时,会有较好的增强结果,可适当根据待增强图像的平均亮度调整α的值,以获得更好的增强效果。
4 结束语
本文在分析现有动态直方图技术的缺陷和研究低照度图像直方图的特性后,提出了一种结合直方图分布范围的分割方式,并通过设置参数m来求取祛噪后的直方图分布范围,达到了合理分配重映射区间和亮度校正的目的。又针对低照度图像增强过程中容易出现的过增强问题,提出了带参数α的调整量来自适应的校正直方图中的较小值,在防止灰度级合并的同时抑制过增强现象。对比实验结果表明,本文所提出的ACDHE算法在提升图像亮度和保留细节信息上优于其它对比算法,增强结果自然,且对于不同类型、不同程度的低照度图像都能取得良好的增强效果。

