移动机器人未知环境下无线基站搜索

廖列法，张幸平+，李 帅，杨翌虢

(1.江西理工大学 信息工程学院，江西 赣州 341000；2.斯旺西大学 工程学院，英国 威尔士 斯旺西 SA1 8EN)

0 引 言

许多生物通过感知气味信息的变化可以进行自主活动。例如飞蛾利用气味可以成群飞行[1-3]，鱼和鸟利用气味可以寻找食物[4-6]，虫类利用气味可以搜寻营养物质[7]。与仿生原理类似，机器人主动嗅觉问题[8,9]可理解为机器人通过感知器的反馈进行自主定位、环境探索与自主导航等。在一些特定场景下，通过机器人的感知原理能够完成特定气味源的定位，比如在火场中可利用机器人搜索火灾源以及灭火。因此，特定信号源的定位应用广泛且具有与人互补的优势。

从函数优化的角度理解定位问题：信号源是信号最强的点，即在全局空间寻找信号最强的位置。信号在传输的过程中，受到信号辐射与扩散的影响，信号强度从信号源逐渐向外扩散减弱。若可用函数表示信号强度的变化，则可以通过梯度上升定位信号源。但大多数情况下，无法确定信号源扩散形成的信号场，不能用函数进行表示，而且信号受到干扰的影响，可能形成局部最强。近些年，针对在函数未知的情形下全局寻优，往往可以使用蚁群算法[10,11]、粒子群算法[12]、微粒群优化(PSO)算法[13,14]、遗传算法[15,16]、萤火虫算法[17]等，并且结果大多比较理想。但这些算法往往都源于生物种群思想，即需要很多粒子或者机器人才可以进行搜寻，同时协作要求高、实时性要求强。

天牛须搜索(beetle antennae search，BAS)算法[18,19]是利用天牛觅食行为的仿生机制提出的一种全局寻优方法。它没有梯度信息，可在函数未知的情况下，通过单个个体实现高效寻优。由此，基于BAS提出一种单机器人寻源算法，并应用于未知环境下无线基站搜索。

1 无线基站搜索模型与环境模型

1.1 无线信号模型

无线信号的传播是从信号源(发射端)到信号接收(接收端)的过程。在理想状态下(没有干扰和损耗)，其过程符合自由空间传播模型。但在现实生活中，信号往往会受到各种各样的影响，比如传播过程受到建筑物、无线干扰等影响，其过程符合对数距离损耗模型[20]，公式表达如下

(1)

式中：Ss和Ss0为信号强度(dBm)；s和s0为与发射端的距离，单位为m，并且s0为参考取值，常为1 m;n为路径损耗的速率，一般为常数，取值范围受到环境的影响；Xα为正态随机变量，α为标准差(3.0 dBm-14.1 dBm)，表示如下

Xα～(0,α2)

(2)

式(1)中Ss受到Ss0(距离为1 m时的信号强度)、n(路径损耗，比如周围环境)、s和s0(距离)、Xα(正态随机变量)等影响，对其简化后的模型可表示为

(3)

另外，设置s0=1,Ss0=A， 式(3)可进一步表示为

Ss=A-10nlog10s

(4)

式中：A为常数(s0为1时信号的强度)。对式(4)描述了信号强度Ss与距离s的函数表示，假设信号强度为rssi，s可进一步表示为

(5)

式中：n受到周围环境(理想环境、空旷环境、半空旷环境、密闭环境等)的影响，其参考取值范围见表1。

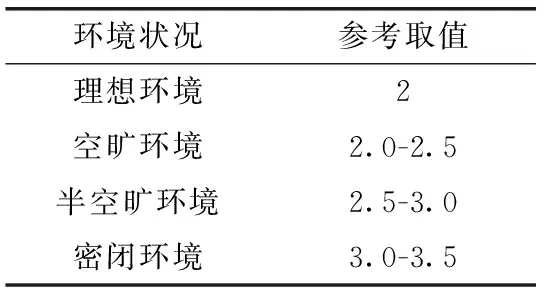
表1 n取值范围

1.2 机器人环境模型

移动机器人所处的环境未知，为方便实验，这里假设分为室内和室外两类，同时将3维空间转换为2维空间。

室内场景的2维表示：如图1所示，为直角坐标系中(20,0)，(20,100)，(80,0)，(80,100)4个顶点组成的区域，其由房间1、房间2、房间3、房间4、房间5、房间6组成，假设空间中的直线为墙壁，空白区域为可行走区域。

图1 室内环境模型

室外场景的2维表示：如图2所示，为直角坐标系中(0,0)，(0,200)，(200,0)，(200,200)4个顶点组成的区域，其包含障碍物1、障碍物2、障碍物3、障碍物4等不规则不同形状的障碍物，同理，空白区域为可行走区域。

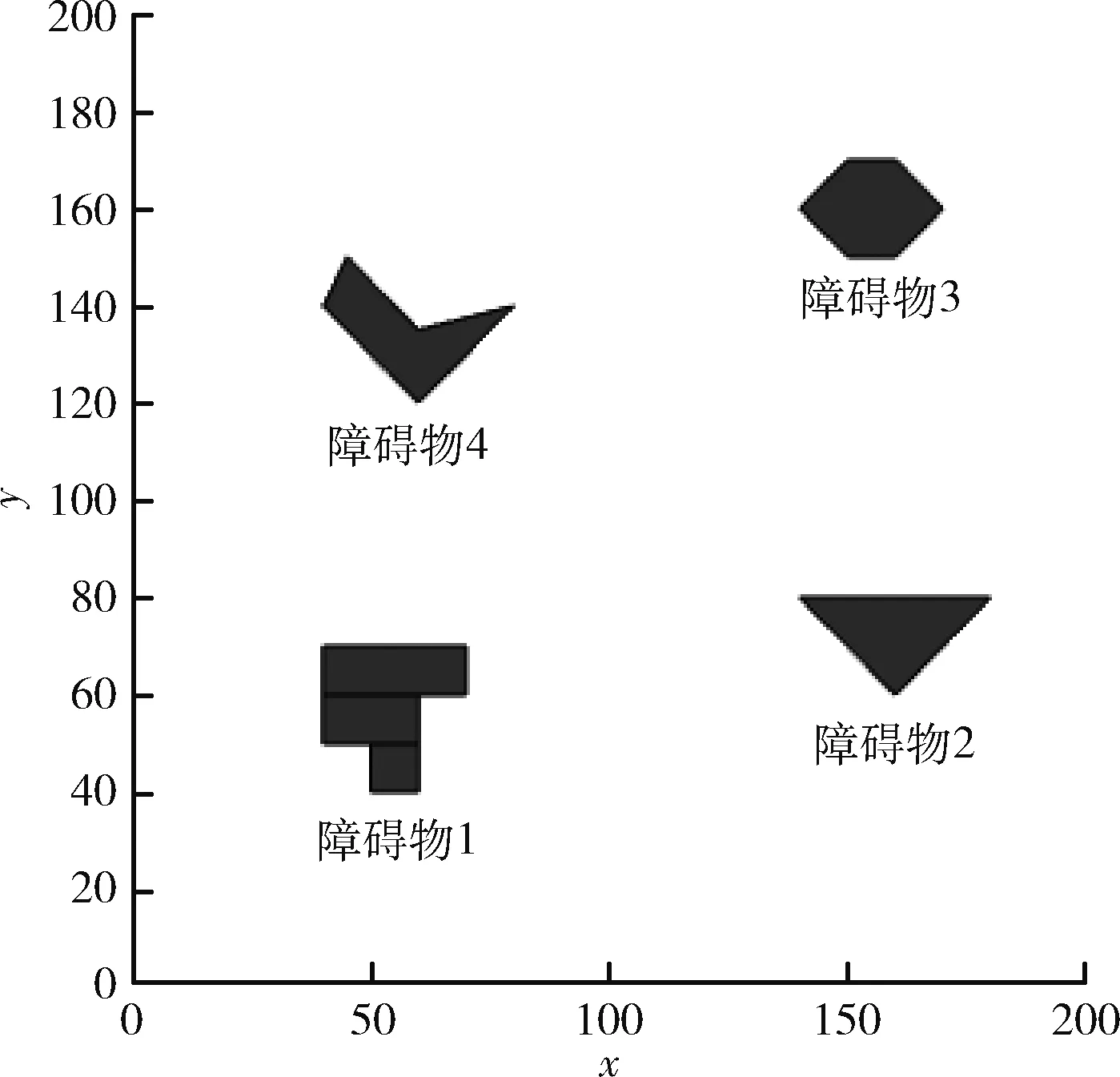
图2 室外环境模型

2 基于天牛须搜索的无线信号搜索算法

2.1 天牛须搜索算法原理

BAS算法是源于天牛觅食的仿生机制，其觅食过程主要是通过两个触角感知食物气味强弱的变化，不断调整行走的方向，最终找到食物。当左边方向的气味更强，则向左边方向行走，反之则向右侧方向行走。行走的方向是根据食物气味的强度动态调整，其觅食过程的函数表达如下：

(1)天牛的起始朝向和两触角间的方向都是随机的，假设为dir，n为空间维数， rands(n,1) 为随机方向向量，对其进行归一化后表示如下

(6)

(2)假设xl和xr为两触角的空间坐标，可表示为

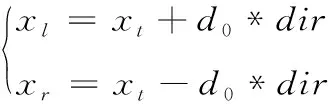
(7)

式中：t为循环次数，xt为t次时天牛的坐标，d0为天牛触角间的距离。

(3)假设f(x) 函数的值为气味的强度， f(xr) 为左边方向的气味函数， f(xl) 为右边方向的气味函数。

(4)天牛每下一步的位置都是根据左右两侧的食物气味强度来动态更新，其函数表示如下

xt=xt-1+δt*dir*sign(f(xl)-f(xr))

(8)

式中：xt-1为上一步天牛的位置，δt为经过t次迭代(每次迭代通过一个衰减系数来更新)后的步长(step)， sign() 为符号函数。式(8)可简化为

(9)

(5)结束？

若找到食物(满足预设条件)或寻找失败(达到迭代最大值)则结束，反之则继续步骤(2)～步骤(4)。

2.2 天牛须无线信号搜索算法原理

从2.1节天牛须搜索算法原理可知，算法以初始位置、初始方向、步长、步长衰减系数等作为参数。首先，以初始参数计算天牛的下一步运动位置。然后，把初始位置和下一步位置理解为左右两触角的位置(位置1和位置2)，两位置之间的距离为步长。根据位置1和位置2感知的无线信号强度来动态调整运动轨迹，始终朝着信号更强的方向运动。每一次运动后，都把下一步位置和上一步位置更新为位置1和位置2，并通过步长衰减系数更新步长，如此循环迭代，直到搜索结束，其具体过程如下：

(1)机器人的参数：假设x0为起始位置，step为每一步运动的距离，dir为运动的方向。x1为算法计算的下一步位置的坐标。根据式(9)，x1可表达为

x1=x0+step*dir

(10)

(2)x0和x1为左右两个方向的坐标， f(x0) 为左边(x0)方向的函数， f(x1) 为右边(x1)方向的函数。

(3)根据x0和x1的无线信号强度值，计算下一步的运动位置x2(根据式(9)的位置更新策略)，表示为

(11)

(4)建立位置迭代模型，其更新策略可表示为

(12)

其中，x0(位置1)表示为位置x0和x1接收到的信号强度更强的位置，x1(位置2)表示为以x0、x1、 f(x0)、 f(x1) 为参数，根据BAS算法计算出机器人下一步的运动位置。

(5)结束？

若找到食物(满足预设条件)或寻找失败(达到迭代最大值)则结束，反之则继续步骤(2)～步骤(4)。

2.3 天牛须无线信号搜索算法流程

(1)初始化:初始化x0(记为位置1)、dir(运动方向)、step(每一步的运动距离)。

(2)计算位置2:把初始参数x0、dir、step代入式(10)，得出x1， 记为位置2(下一步的运动位置)。

(3)x1更新:如果x1为无效坐标(坐标在障碍物空间内或受到障碍物影响需要绕行)，则x1更新为与障碍物的交汇坐标。反之，x1为有效坐标，直接进行下一步。

(4)计算位置x2:把x0、x1、dir、step代入式(11)，得出x2(下一步运动位置)。

(5)x2更新:同理(3)，若x2为无效坐标，则x2更新为与障碍物的交汇坐标。反之，x2为有效坐标，直接进行下一步。

(6)更新位置1和位置2:根据x1和x2的无线信号强度来动态调整运动轨迹，始终朝着信号更强的方向运动。x1和x2的更新策略见式(12)。

(7)预期位置:若找到无线信号源(满足预设条件)或寻找失败(达到迭代最大值)则结束，反之则继续步骤(4)～步骤(7)。

(8)结束。

图3为天牛须无线信号搜索算法的流程。

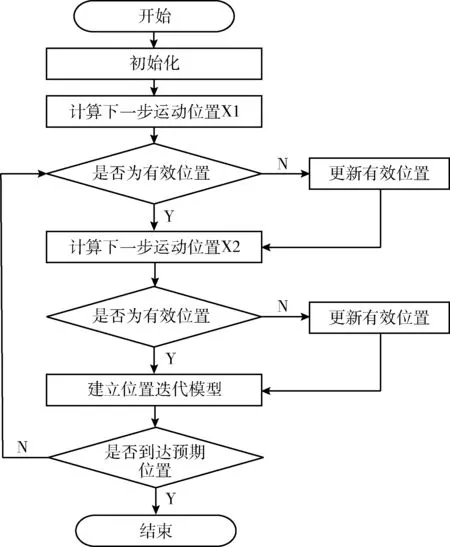
图3 算法流程

3 实验仿真与算法分析

实验分为室内场景和室外场景，在仿真工具(MATALAB_R2017b)上进行模拟实验，记录天牛须无线信号搜索算法计算的每一次运动位置(坐标)，每一次实验所有点坐标的连接曲线即为运动轨迹。

3.1 室内环境

图4为室内场景中实验的结果。设图4按上到下的顺序依次记为图4(a)、图4(b)、图4(c)、图4(d)。图4(a) 的初始参数：路径衰减因子n为2、初始坐标为(22，15)、步长为3(衰减系数0.98)、信号源为坐标(70,90) 处的正方形、迭代最大值为100、误差值为1。图4(b) 的n为2.5、初始坐标为(48，10)。图4(c)的n为3，初始坐标为(28，41)。图4(d)的n为3.5，初始坐标为(26，90)。图4(b)、图4(c)和图4(d)的其它参数与图4(a)一致。图4(a)～图4(d)表明不同的环境(理想环境、空旷环境、半空旷环境、密闭环境)中不同的路径衰减速率n(2、2.5、3、3.5)下都可以通过BAS算法成功搜索到无线信号源的位置。

图4 室内场景不同起点和相同终点时的实验结果

3.2 室外环境

图5为室外场景的实验结果。设图5按上到下的顺序依次记为图5(a)、图5(b)、图5(c)、图5(d)。图5(a) 的初始参数：路径衰减因子n为2、初始坐标为(7,40)、步长为20(衰减系数0.98)、信号源为坐标(185,185)处的正方形、迭代最大值为100、误差值为1。图5(b)的n为2.5、初始坐标为(34,75)。图5(c)的

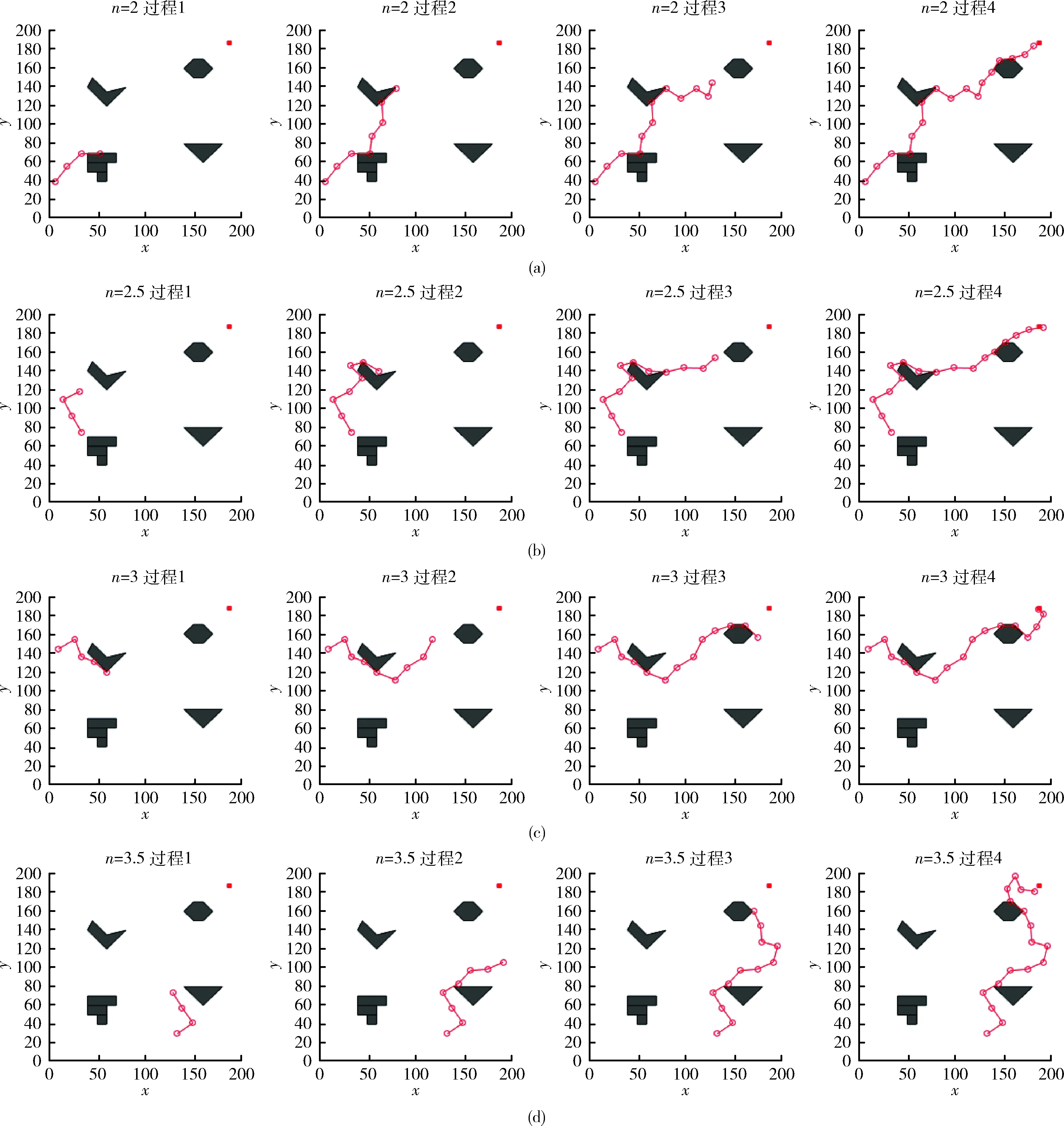
图5 室外场景不同起点和相同终点时的实验结果

n为3，初始坐标为(10,144)。图5(d)的n为3.5，初始坐标为(133,30)。图5(b)、图5(c)和图5(d)的其它参数与图5(a)一致。图5(a)～图5(d)表明不同的环境(理想环境、空旷环境、半空旷环境、密闭环境)中不同的路径衰减速率n(2、2.5、3、3.5)下都可以通过BAS算法成功搜索到无线信号源的位置。

3.3 天牛须无线信号搜索算法分析

3.3.1 实验结果分析

为保证实验的有效性和可靠性，室内场景中针对路径衰减因子n的每一次取值(2,2.5,3,3.5)都分别执行30、60、120次，记录下每一次实验的结果并对实验数据进行统计，统计结果见表2。从表2可知，n的取值对整个实验的结果影响不大，随着实验次数的增加，机器人移动的坐标数趋于稳定，说明算法在室内场景中不同起点的情况下有效。

表2 室内场景的统计结果/步数

同样，室外场景中也针对n的每一次取值都分别执行30、60、120次，记录下每一次实验的结果并对实验数据进行统计，统计结果见表3。从表3可知，n的取值对整个实验的结果影响不大，随着实验次数的增加，机器人移动的坐标数趋于稳定，说明算法在室外场景中不同起点的情况下有效。

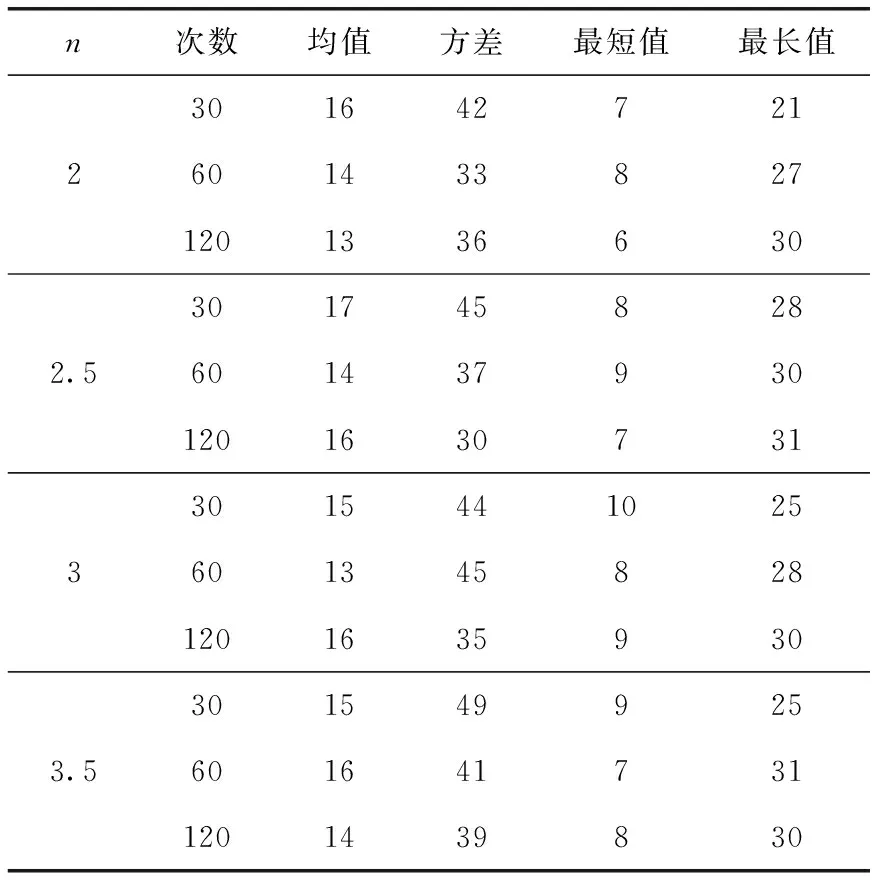
表3 室外场景的统计结果/步数

3.3.2 与经典算法对比分析

随机选取室内与室外场景下连续测试120次，然后对120次的实验结果取平均，并将其作为搜索无线信号源的位置，再与PSO算法、GA算法进行对比，结果见表4。从表4中可知，BAS与PSO、GA算法对比中可知，BAS的收敛速度最快，验证了算法的优越性。

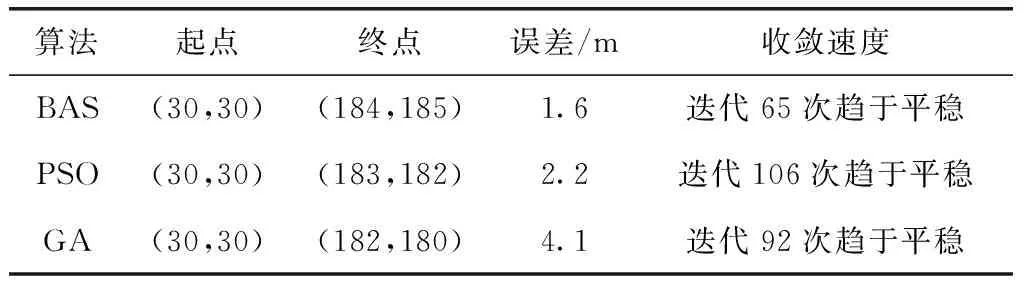
表4 3种算法对比

3.3.3 算法时间复杂度分析

从2.2节天牛须无线信号搜索算法原理可知，算法包含动态计算无线信号与机器人之间的距离和不断优化下一步运动位置两个部分，故其时间复杂度是这两部的时间复杂度。假设一次搜索过程中，计算下一步运动位置的次数(节点数)为M， 则时间复杂度为o(n2)。

证明[21]：第一部分(算法在优化下一步运动位置)：计算f(x) 的最优值(信号最强)时，共计算n次，则时间复杂度为o(n)； 第二部分(动态计算节点距离)：为了提高算法的准确性与可靠性，每个节点的取值都是m次后取平均，则时间复杂度为o(n×m)。 算法中m=n， 所以其时间复杂度为

o(n×m+n)≈o(n2)

(13)

动态计算搜索节点与无线信号源之间距离的时间复杂度为o(M)， 若M个节点同时搜索，则时间复杂度为o(M×n2)， 但整个算法中只需要一个机器人完成搜索，即只需要确定单个个体的位置。通过以上的分析可得，算法在单个个体搜索过程中的时间复杂度为o(n2)。

4 结束语

通过天牛须无线信号搜索算法，机器人在未知环境下进行无线信号源搜寻，只需要一个信号感知器，简单方便的同时实现了高效的全局寻优。实验结果表明，机器人在仿真的室内与室外环境中都可以完成预定的无线信号源搜寻任务，同时结合与经典算法的对方分析，验证了算法的优越性。后续将在其它此类的应用场景中进一步改善优化算法。