基于重采样与属性约简的多模态选择性集成学习

江 峰，李 瑞，张友强，杨爱光

(青岛科技大学 信息科学技术学院，山东 青岛 266061)

0 引 言

集成学习的目的是训练多个不同的个体分类器，并通过某种组合策略(例如，投票)将这些个体分类器集成在一起，从而生成泛化能力更强的集成分类器[1,2]。如果只是选择一部分的个体分类器来生成集成分类器，那么这种集成学习策略就称为“选择性集成”[3]。选择性集成算法需要对个体分类器进行扰乱，按照扰乱手段的不同，可以将现有集成算法分成两大类：基于单模态扰乱的选择性集成算法(简称“单扰乱算法”)和基于多模态扰乱的选择性集成算法(简称“多扰乱算法”)。单扰乱算法只利用一种策略来将数据集打乱，以得到多个不同的个体分类器[4,5]。多扰乱算法则利用多种策略来将数据集打乱，以得到多个不同的个体分类器[6]。相对于单扰乱算法而言，多扰乱算法具有显著的优势，即更容易实现个体分类器的多样性。正是由于上述优势，多扰乱算法得到了广泛研究与应用[7,8]。

本文针对多扰乱算法进行研究，利用两种策略分别将数据集的样本与特征空间打乱，从而得到一种选择性集成算法SE_RSAR。该算法的大体思路如下：①通过随机的重复采样策略将数据集的样本空间打乱，产生多个采样集；②对任意一个采样集Sample，通过基于相对决策熵的属性约简策略先对Sample进行约简，然后利用约简后的采样集训练一个个体分类器；③从第②步所生成的所有个体分类器中，利用贪婪机制[9]挑选出若干个性能较好且差异性较大的个体分类器；④通过投票，把第③步所挑选出的个体分类器组合在一起，得到集成分类器。

实验采用KNN算法来训练个体分类器，并在UCI数据集上将SE_RSAR算法与现有的同类型集成学习算法性能相比较。实验结果表明，SE_RSAR算法能够取得更好的分类效果。

1 粗糙集的基本知识

本节引入与粗糙集理论相关的一些主要概念。在粗糙集中，一般使用信息系统来存储数据(关于信息系统的详细定义可参考文献[10,11])。当我们将一个信息系统中的属性集分成条件属性集和决策属性集时，就得到了另外一个概念：决策表(关于决策表的详细定义也可参考文献[10,11])。

在粗糙集领域，“知识”代表着一种分类的能力，知识通常由不可分辨关系来刻画。不可分辨关系作为粗糙集理论的基础，假定关于论域的某类知识，并采用属性和属性值来描述论域中的对象，若两个对象(或对象集)存在相同的属性及属性值，则称它们之间存在不可分辨关系。给定一个决策表DT=(U,C,D,V，f) 和任意的条件属性子集B(其中，B⊆C)， 论域U上的二元关系IND(B)={(x,y)∈U×U∶∀b∈B,f(x,b)=f(y,b)} 被称为不可分辨关系。不可分辨关系本身也是一种等价关系。对于论域U中的任意一个元素u，u在不可分辨关系IND(B) 下所属的等价类被定义成： [u]B={v∈U∶(u,v)∈IND(B)}。

利用不可分辨关系，可以进一步定义正区域、粗糙度、属性依赖度等概念，其中，D的B-正区域是指U中所有根据关系U/IND(B) 可以准确划分到U/IND(D) 中的等价类去的对象集合,具体定义见文献[10-12]，另外，粗糙度和属性依赖度的具体定义也同样见文献[10-12]。

2 基于相对决策熵的属性约简

属性约简是粗糙集理论中的一个重要研究课题，它是指在保持分类能力不变的前提下，将决策表中不影响决策或者分类的多余属性去掉。在Pawlak提出的经典粗糙集模型中，通常使用代数表达式来定义粗糙集中的许多基本概念。粗糙集理论认为，知识的粗糙性可以通过集合之间的包含关系和代数中的等价关系来描述。但是，用这种方式很难从本质上来理解知识的粗糙性。为了深入刻画粗糙集中信息与粗糙度之间的关系，许多研究人员将信息熵引入到粗糙集中[13]。本文将在粗糙集中引入一种新的信息熵——相对决策熵，并利用其来进行属性约简[14,15]。

与已有文献中所提出的关于信息熵的定义不同，相对决策熵的定义与粗糙度这一概念有关[15]。

定义1 相对决策熵:给定决策表DT=(U,C,D,V,f)， 令U/IND(D)={D1,…,Dm} 表示不可分辨关系IND(D)对U的划分。对任意B⊆C，D相对于B的决策熵RDE(D,B) 定义为

其中，γB(D) 表示决策属性集D对B的依赖度，ρB(Di) 表示集合Di在关系IND(B)下的粗糙度， 1≤i≤m。

在定义1的基础上，可以进一步定义基于相对决策熵的属性约简和基于相对决策熵的属性重要性，具体定义可参考文献[15]。

接下来，我们给出一个启发式属性约简算法(即算法1)，用于在给定的决策表中计算出基于相对决策熵的约简。

算法1： 基于相对决策熵的约简计算

输入： 决策表DT=(U,C,D,V,f)

输出： 约简R

算法初始化： 令Core←∅,R←∅

(1) 计算划分U/IND(C),U/IND(D) 和U/IND(C∪D)。

(2) 计算相对决策熵RDE(D,C)。

(3) 对每个a∈C， 反复执行：

(3.1) 计算相对决策熵RDE(D,C-{a})；

(3.2) 如果RDE(D,C-{a})>RDE(D,C)， 则令Core←Core∪{a}。

(4) 令R←Core。

(5) 如果R=∅， 则令Temp←RDE(D,C)+1， 否则，令Temp←RDE(D,R)。

(6) 当Temp≠RDE(D,C) 时， 反复执行：

(6.1) 对每个b∈C-R， 反复执行：

(I) 计算RDE(D,R∪{b});

(II) 计算b相对于R和D的重要性SGF(b,R,D)=RDE(D,R)-RDE(D,R∪{b})。

(6.2) 从C-R中选择重要性最大的属性bmax(如果有多个属性同时具有最大的重要性，则选择使得γ{bmax}(D) 值最大的bmax)。

(6.3) 令Temp←RDE(D,R∪{bmax}),R←R∪{bmax}。

(7) 对每个ai∈R(其中，下标i的取值从 |R|-1 逐步递减到|Core|)， 反复执行：

计算RDE(D,R-{ai})， 如果RDE(D,R-{ai})=RDE(D,C)， 则将元素ai从集合R中移去。

(8) 返回约简R。

在算法1中，我们采用一种预先对论域U进行计数排序，然后再计算划分U/IND(B) 的策略(其中，B⊆C是任意一个属性子集)，以此使得计算U/IND(B) 的时间复杂度为O(|B|×|U|)。 最坏情况下，算法1的时间复杂度为：O(|C∪D|2×|U|)， 空间复杂度为O(|C∪D|×|U|)。

3 SE_RSAR算法

Bagging、Boosting和RSM(random subspace me-thod) 是3个非常具有代表性的单扰乱算法，其中，前面两个算法利用“样本空间扰乱”这种策略来将数据集打乱；第三个算法则利用“特征空间扰乱”这种策略来将数据集打乱。通常，单扰乱算法在提升个体分类器的多样性方面存在不足。针对这一不足，本文设计出多扰乱算法SE_RSAR[16-18]，利用两种策略分别将数据集的样本与特征空间打乱。SE_RSAR算法可分成4个阶段：①样本空间打乱阶段。通过随机的重复采样策略将数据集的样本空间打乱，产生多个采样集；②特征空间打乱阶段。对任意一个采样集Sample，通过基于相对决策熵的属性约简策略先对Sample进行约简[19]，然后利用约简后的采样集训练一个个体分类器；③贪婪搜索阶段。从第②阶段所生成的所有个体分类器中，利用贪婪机制挑选出若干个性能较好且差异性较大的个体分类器；④投票阶段。通过投票，把第③阶段所挑选出的个体分类器组合在一起，得到集成分类器。

SE_RSAR算法的第③阶段利用贪婪机制[20]挑选出若干个性能较好且差异性较大的个体分类器，具体过程如下：首先，利用给定的验证集去验证每一个待选的个体分类器的性能，根据这些个体分类器的性能从高到低对它们进行排序，并将性能最好的一个个体分类器挑选到分类器集合E中[21]；其次，从所有剩下的待选个体分类器中挑选出当前最优的个体分类器加入到E中，挑选标准为：相对于其它的待选个体分类器，将最优个体分类器加入到E中之后，由E中个体分类器所组合而成的集成分类器具有最好的性能；第三，重复执行第二步，每次挑选出当前最优个体分类器加入到E中之后，都把由E中元素所组合而成的集成分类器的性能保存起来。通常，集成分类器的性能一开始会不断地增加，在获得最高值之后将会逐渐地下降；第四，将那些在集成分类器的性能获得最高值之后加入到E中的个体分类器从E中剔除。

下面，给出SE_RSAR的伪代码。

算法2： 多扰乱算法SE_RSAR

输入： 给定的训练集与验证集；待选的个体分类器数量M。

输出： 集成分类器EC。

算法初始化： 将集合E、R和B都初始化为空集， 并且将变量num初始化为0。

(1) 对每一个i∈{1,2,…,M}， 循环执行下面的语句：

(1.1) 针对给定的训练集，通过随机的重复采样策略对其进行采样， 得到一个采样集Si；

(1.2) 使用算法1在集合Si上产生一个约简ri， 将ri作为一个元素加入到集合R， 并且利用ri对Si进行特征选择， 从而得到特征选择之后的采样集Sri；

(1.3) 在采样集Sri上通过预先确定的分类算法训练一个个体分类器bi， 并且将bi作为一个元素加入到待选个体分类器集合B中。

(2) 对每一个i∈{1,2,…,M}， 循环执行下面的语句：

(2.1) 针对给定的验证集， 通过约简ri对其进行特征选择， 从而得到特征选择之后的验证集Vri；

(2.2) 计算个体分类器bi在验证集Vri上的分类精度。

(3) 将B={b1,…,bM} 中的所有待选个体分类器按照其分类精度从高到低进行排序。

(4) 挑选出B中排在第一位的个体分类器b1， 将b1作为选中的个体分类器加入到集合E中， 并从集合B中剔除b1。

(5) 如果集合B包含两个或两个以上的元素， 则循环执行下面的语句：

(5.1) 对于B中的任意一个个体分类器b， 将E∪{b} 中所有的个体分类器组合成一个集成分类器， 并验证该集成分类器在给定验证集上的分类精度Pb；

(5.2) 挑选出B中的个体分类器bmax， 挑选标准为： 由E∪{bmax} 中个体分类器所组合而成的集成分类器的分类精度Pbmax最大。令E←E∪{bmax},B←B-{bmax}, Array[num]←Pbmax, num←num+1。

(6) 把Array中值最大的元素的下标赋值给变量h， 并且将集合E中所有下标在h之后的个体分类器都从E中剔除。

(7) 通过投票， 把E中的个体分类器组合在一起， 得到集成分类器EC。

(8) 返回集成分类器EC。

4 实验结果

为了验证SE_RSAR算法的性能，我们在8个UCI数据集上进行了实验，其中，基分类器采用1NN(1-最近邻)分类算法来训练。表1给出了这8个UCI数据集的详细信息。

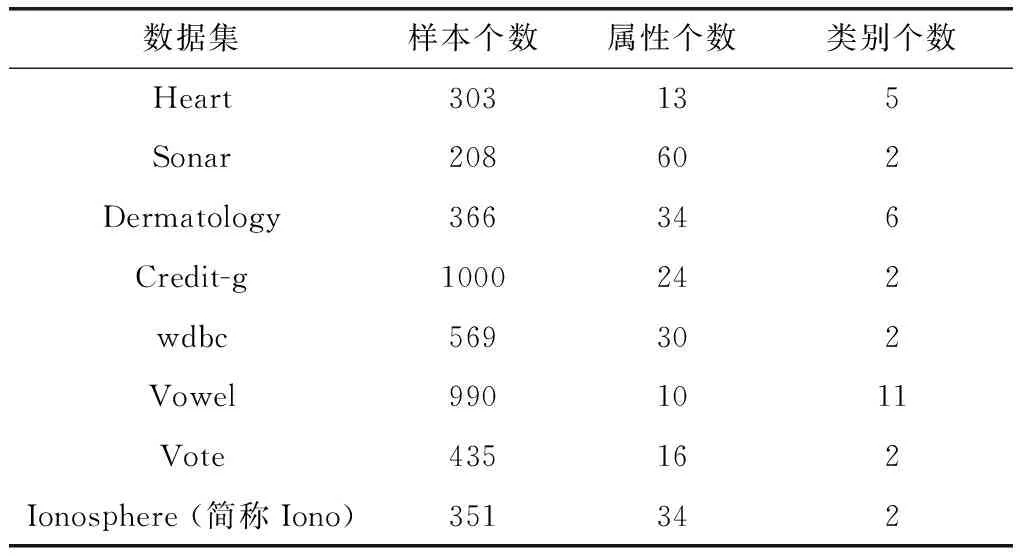
表1 8个UCI数据集

本文所采用的分类评估指标为：分类精度(Accuracy)。分类精度的具体定义如下：对于给定的测试集T，分类器正确分类的样本数量与T中总的样本数量之比。假设当前考虑的是一个二分类问题，分类精度可以通过表2所示的混淆矩阵来进行计算，即

Accuracy=(TP+TN)/(TP+FN+FP+TN)

我们采用Java语言实现了SE_RSAR算法。实验中，对于数据集中的连续型属性，我们预先使用等宽离散化算法进行离散化处理，其中，区间数设置为5。对于一个给定的数据集T，我们将T随机分为一个训练集(T中50%的数据)和一个测试集(剩余50%的数据)。另外，由于SE_RSAR 算法需要使用一个验证集来选择一组性能较好且差异性较大的个体分类器，因此，我们还从训练集中随机选取60%的样本作为验证集。对于SE_RSAR算法，我们还需要设定待选个体分类器的数量，在实验中，待选个体分类器的数量统一设置为30。

在实验过程中，我们分别采用了两种不同的采样方法来获取采样集：无放回采样和有放回采样。在使用无放回采样时，我们采取了3种不同的采样比例(90%、95%和98%)来对训练集进行随机采样。在使用有放回采样时，我们同样采取了3种不同的采样比例(90%、95%和100%)来对训练集进行随机采样。表3给出了在使用无放回采样时SE_RSAR算法在各个数据集上以及不同采样比例下的分类性能。表4则给出了在使用有放回采样时SE_RSAR 算法在各个数据集上以及不同采样比例下的分类性能。

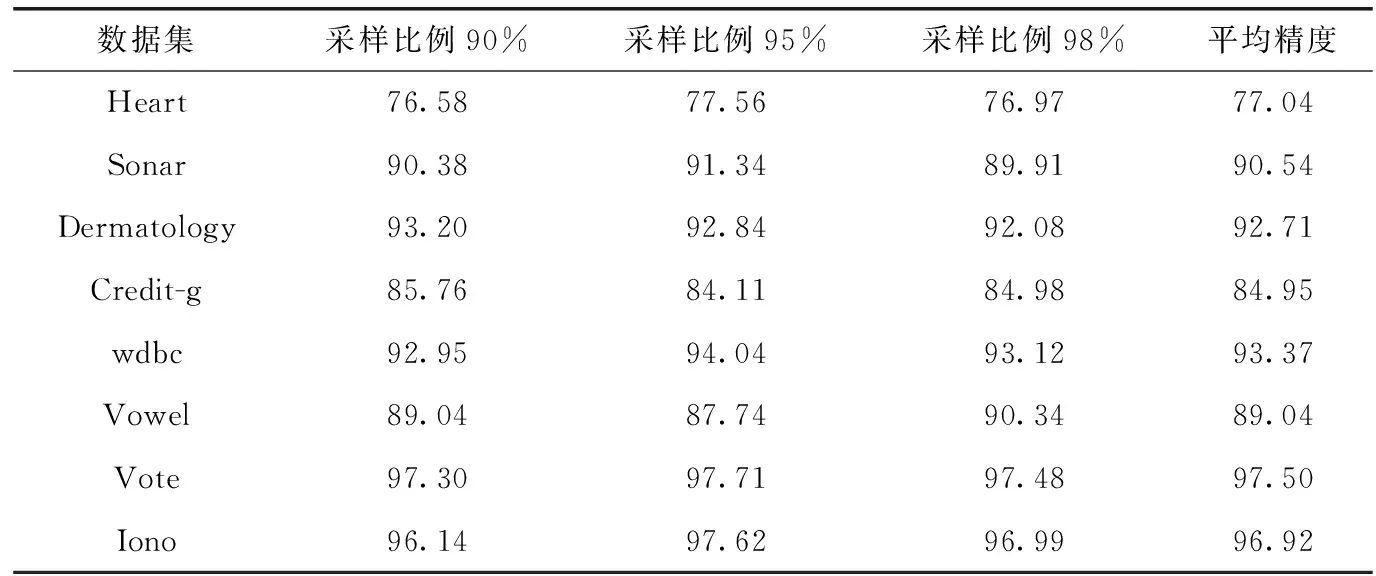
表3 无放回采样时SE_RSAR算法的性能/%

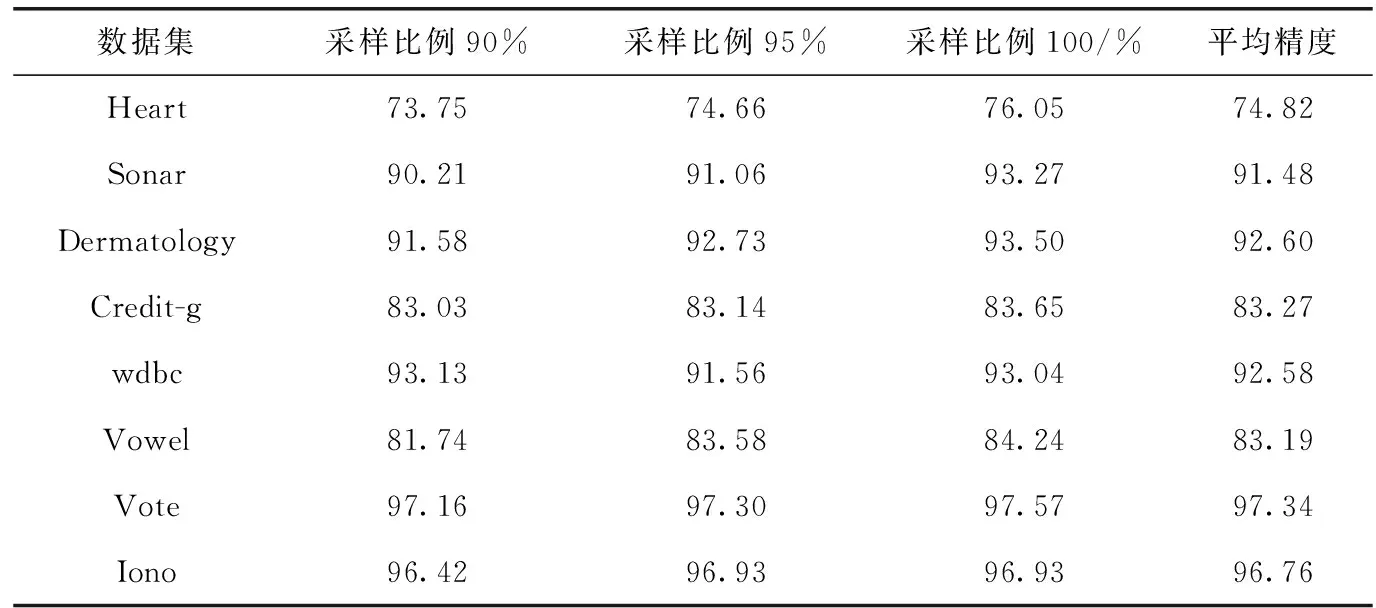
表4 有放回采样时SE_RSAR算法的性能/%

在表3和表4中，第2列-第4列的实验结果都是在重复执行100次之后，取这100次实验结果的平均值。另外，最后一列结果为第2-第4列结果的平均值，即SE_RSAR算法在3种不同采样比例下的平均精度。

从表3可以看出，对于无放回采样而言，95%的采样比例在5个数据集上取得了最高的分类精度，90%的采样比例则在两个数据集上取得了最高的分类精度，98%的采样比例只在“Vowel”数据集上取得了最高的分类精度。上述结果表明，95%的采样比例比较适合于无放回采样。另外，从表4可以看出，对于有放回采样而言，100%的采样比例在7个数据集上取得了最高的分类精度，而90%的采样比例只在数据集“wdbc”上取得了最高的分类精度。上述结果表明，100%的采样比例比较适合于有放回采样。

如果将表3和表4中的数据进行对比，我们可以看出，SE_RSAR算法在无放回采样下的性能要优于其在有放回采样下的性能，这是因为在大部分数据集上(除了“Sonar”数据集之外)，采用无放回采样的SE_RSAR算法，其平均精度要高于采用有放回采样的SE_RSAR算法。

接下来，我们将SE_RSAR算法与两种常用的单模态集成算法(Bagging和RSM)以及一种多模态集成算法(Bagging-RSM)进行对比，以验证SE_RSAR算法的性能。为了确保比较的公平性，这里SE_RSAR算法将同样采用在Bagging和Bagging-RSM中所使用的自助采样方法，即对训练集进行有放回并且采样比例为100%的采样。对于Bagging、RSM和Bagging-RSM，我们直接使用WEKA[22]中所提供的算法来进行实验，所有参数均设置为WEKA中的默认值。

在表5中，我们给出了不同算法的分类结果。

表5 不同算法的分类精度对比/%

在表5中，1NN表示不使用集成方法，而是直接采用单个分类器来进行分类。从表5可以看出，SE_RSAR算法在7个数据集上的分类精度都要优于其它算法，唯一的例外是数据集“Dermatology”，不过，在该数据集上，SE_RSAR 算法的性能仍然要比Bagging和1NN方法好。因此，从总体上看，本文提出的SE_RSAR算法其性能要优于现有的集成学习方法。另外，可以看出，在“Iono”，“Sonar”和“ Vowel”这3个数据集上，Bagging的性能比单分类器算法1NN还要差，而在其它数据集上，Bagging相对于1NN而言其性能提升得也不明显。上述结果表明，单模态的集成方法很多时候不足以提升集成学习的整体性能。

5 结束语

为了增加个体分类器之间的差异性，本文提出一种基于重采样[23]和属性约简[24]的多模态选择性集成学习方法。该方法利用重采样技术来扰乱样本空间，并通过基于相对决策熵的属性约简方法来扰乱特征空间，通过这种多模态的扰乱策略可以有效提升个体分类器之间的差异性。另外，我们还提出了一种基于贪婪机制的个体分类器选择方法，可以进一步提升集成分类器的性能。实验结果表明，本文所提出的SE_RSAR算法其性能要优于当前的单模态及多模态集成算法。

基于相对决策熵的属性约简方法是在Pawlak的经典粗糙集模型下所提出的。由于经典粗糙集模型只能用于处理离散型属性，因此，SE_RSAR算法需要利用一个离散化过程将所有连续型属性转换为离散型属性。但是，属性的离散化可能会导致信息丢失。在下一步的工作中，我们将考虑把SE_RSAR算法扩展到邻域粗糙集模型[25-27]中，该模型可以同时处理连续型和离散性属性，从而不需要对连续型属性进行离散化处理。