相交轴转子系统当量化建模与扭振响应分析*

陈立满 杨大炼† 蒋玲莉 李学军

（1.湖南科技大学机械设备健康维护湖南省重点实验室，湘潭 411201）（2.佛山科学技术学院机电工程学院，佛山 528225）

引言

转轴及轴上旋转部件和支撑部件共同构成转子系统.最典型的转子系统是Jeffcott转子，此类转子系统的转轴保持同体、同速、同轴线等特性.由于结构、传动等方面的需求，转子系统可以是不同体的两组轴或多组轴.一种情况是通过联轴器联接，该类转子系统转轴不同体、但同转速、同轴线；另一种是通过齿轮联结，又可分为圆柱齿轮联结的平行轴转子系统和锥齿轮联结的相交轴转子系统，其中相交轴转子系统由螺旋锥齿轮联结，广泛应用于航空、航海等领域.

由于齿轮副的存在，转子系统将受到明显的啮合激励，啮合刚度、阻尼不仅使转子系统建模困难，而且对动力学特性产生极大影响，且不同类型的齿轮副产生的啮合激励差异较大.目前圆柱齿轮联结的平行轴转子系统动力学特性的研究较详尽.洪清泉等［1］在对传统的齿轮副扭转振动模型进行动力学等效变换的基础上，研究了齿轮传动转子系统的动态响应.蒋庆磊等［2］建立了齿轮传动多转子耦合系统动力学分析的通用模型，给出了建立多转子耦合振动模型的方法以及振动特性分析方法.张义民等［3］推导了三平行轴齿轮转子的啮合刚度矩阵，通过建立有限元模型，发现了系统不平衡响应会在非临界转速处进行积累，出现最大振动峰值的现象.Tang等［4］建立了一种新的简化扭转振动动力学模型，研究了复合行星混合动力系统的扭转振动特性.Zhang等［5］建立了五平行轴齿轮转子有限元模型，研究了转子系统在外载荷作用下，轴承刚度变化引起的临界转速和共振特性的变化.

直升机尾传动系统是典型的锥齿轮联结的相交轴转子系统，朱自冰等［6］、许兆棠等［7，8］使用集中质量和模态叠加法建立了直升机尾传动系统动力学模型，并获得传动系统的临界转速和模态振型.柴山，范磊等［9，10］推导了考虑弯扭耦合的齿轮啮合单元的传递矩阵，将传递矩阵法应用于研究存在啮合耦合的多级齿轮传动系统弯扭耦合振动.为了建立更精确的相交轴齿轮传动系统模型，许多学者将多种建模方法整合在一起处理由于螺旋锥齿轮的存在而产生的问题.Li等［11］首先建立离散的集中质量模型，然后根据锥齿轮啮合边界条件利用拉格朗日方程建立弯扭轴耦合动力学模型.虽然集中质量法计算速度快，计算效率高，但它通常使用有限的坐标，不能完全准确地反映传动系统的结构特性，Hua［12］将集中质量法和有限元法结合起来，提出一种改进的集中质量建模方法.锥齿轮联结的相交轴转子系统，是一类不同体、不同转速、不同轴线的转子系统，在空间中改变动力传递的方向，不同传动轴具有不同的局部坐标系，角位移、角速度和转动惯量等无法在全局坐标系下度量；尾传动系统的三组传动轴由两级减速器联结，两级减速器是螺旋锥齿轮副，产生的啮合激励更加复杂，且其装配精度更难控制，导致建模、临界转速和振动响应分析更加困难.国内外学者在研究齿轮转子系统的扭振动力学特性时，常对转子系统做当量化处理.王琪［13］、Chen等［14］提出了齿轮转子的当量化建模思想和理论.Wu等［15］推导了多分支齿轮转子系统当量化建模公式.Tang等［16］应用当量化建模方法建立了混合动力汽车传动系统扭振等效模型，Senjanović等［17］、Murawski等［18］将当量化建模方法应用到舰船推进系统建模中.

齿轮转子系统在工作过程中不可避免的产生扭振，因此进行传动系统扭振响应研究很有必要.Han等［19］通过参数化研究，对实际船舶发生高扭转振动的原因进行了分析.Zhao等［20］研究了具有两级行星齿轮级和一级平行齿轮级的风力发电机组齿轮箱的扭振.王飞鹏等［21］改进了基于扭矩激励的多支承转子系统力学模型，分析了无扭矩激励和暂态扭矩激励作用下，多支承转子系统的振动响应.廖鹏飞等［22］采用经典的频域集总参数多质点模型研究了冰载荷冲击下船舶推进轴系扭振响应.

本文以某型直升机尾传动系统作为研究对象，采用当量转化建模方法对相交轴转子系统做等效处理，进而使用DyRoBes软件建立相交轴齿轮转子系统有限元模型，从转子动力学角度研究相交轴齿轮转子系统扭振响应规律，可为齿轮联结相交轴转子系统的机构优化设计和运行维护提供参考.

1 齿轮联结相交轴转子系统有限元模型

论文以典型相交轴齿轮联结转子系统——直升机尾传动系统为研究对象，直升机尾传动系统由水平轴（HS）、中间减速器、尾斜轴（OS）、尾减速器和尾桨轴（TRS）组成，见图1.其中，中间减速器与尾减速器均由螺旋锥齿轮副构成［23］.表1给出了中、尾减螺旋锥齿轮的主要参数，其中三根组成轴的长度分别为LHS=2400mm，LOS=LTRS=800mm，外径D=90mm，内径d=80mm，材料为结构钢，弾性模量E=206GPa，ρ=7800kg/m3.

图1 某型直升机尾传动系统三维实体模型Fig.1 3D model of a helicopter tail drive system

表1 尾传动系统各齿轮主要参数Table1 Main parameters of each gear in the tail drive system

1.1 齿轮联结相交轴转子系统当量化有限元建模方法

有限元法的基本思想是将连续体看成有限个基本单元在节点处彼此相连接的组合体，使问题变成有限自由度的力学问题，从而借助线性方程组求解.对于扭振而言，有限元法将一个连续扭振问题离散化成有限自由度的振动问题，扭振系统的离散化力学模型包括质量元件、弹性元件和阻尼元件.对于螺旋锥齿轮联结，假设齿轮采用刚性支撑，啮合的螺旋锥齿轮副等效为由弹性单元和阻尼单元联结的等效圆盘，建立两自由度齿轮副动力学模型，见图2.

图2 螺旋锥齿轮副动力学模型Fig.2 Dynamic model of spiral bevel gear pair

Ip，Ig，Tp，Tg，θp，θg，Rp，Rg分别是主从动齿轮的转动惯量、扭矩、扭转角位移和基圆半径，Cm，Km是啮合阻尼和啮合刚度，e（t）为静态传动误差，f（x）为齿侧间隙函数，根据动力学模型，参照文献［24］给出螺旋锥齿轮副扭振微分方程：

采用DyRoBes有限元软件，进行相交轴转子系统有限元建模.由于相交轴齿轮联结转子系统各级输入轴、联结齿轮、输出轴各部分的转速不同，因此采用当量化建模方法，以输入轴为等效构件，输出轴的惯性、弹性和角位移等使用水平轴上的等效量来表征.当量转化的原则是使当量化后的动能及弹性变形能与当量化前相同［12］.按照式（2）进行计算.

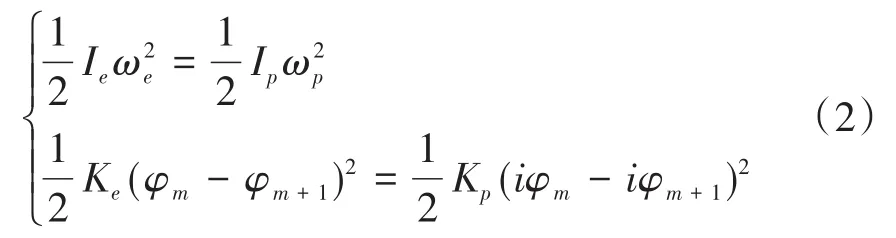
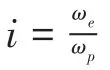
当量转化后相交轴转子系统解决了输入、输出轴不同轴线、转速等问题，为建立有限元模型创造条件.根据已建立的螺旋锥齿轮副动力学模型，结合当量转化建模思想，建立的一级相交轴齿轮转子系统当量化模型如图3所示，图中Km是以扭转刚度表示的综合啮合刚度，Cm是啮合阻尼，Ie表示当量化后从动轮的转动惯量.相交轴转子系统转化为了同速、同轴线转子系统，为从转子动力学角度研究相交轴齿轮传动系统动力学特性提供了便利.

图3 相交轴齿轮转子系统当量化模型Fig.3 Idealized model of intersecting shaft rotor system

为验证本文基于DyRoBes的相交轴齿轮联结的转子系统当量化建模方法的有效性，与文献［8］基于解析法建立的相交轴多级齿轮传动系统分析案列进行对比.根据文献［8］提供的数据，建立基于DyRoBes的当量化有限元模型，计算各阶扭振临界转速，并与文献［8］的分析结果进行对比，如表2所示.表中可见，两种方法误差不大，尤其是低阶误差.由此说明本文提出的基于DyRoBes的齿轮联结的相交轴转子系统当量化建模方法的有效性，可用于直升机尾传动系统动力学建模分析.

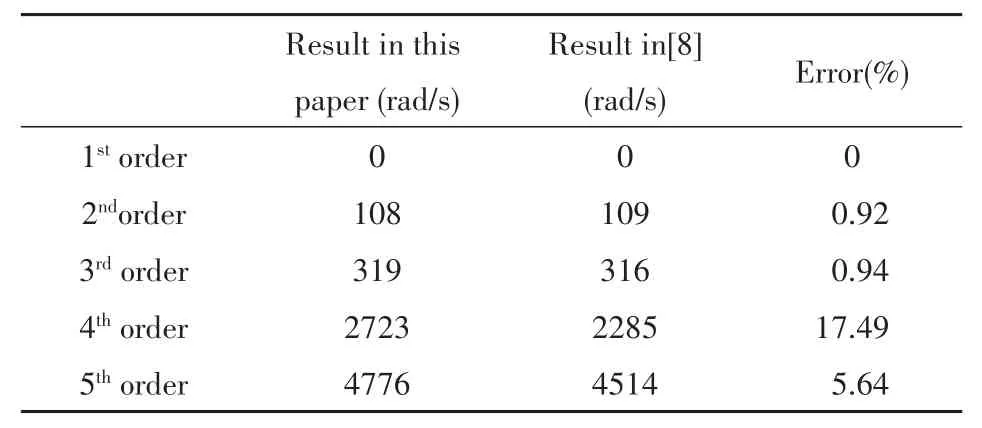
表2 文中方法与现有文献临界转速分析结果对比Table 2 Comparison between the method and the results of natural frequency analysis in existing literatures

1.2 典型相交轴转子系统直升机尾传动系统有限元模型

应用基于DyRoBes的相交轴齿轮联结的转子系统当量转化建模方法，对直升机尾传动系统进行简化处理，把系统各部分向尾传动力输入轴处等效，以水平传动轴为等效构件，将尾斜轴的惯性、弹性、力矩和角位移都用等效构件上的等效量来代替，根据表1中的数据和图1所示的轴系基本结构，采用当量化建模方法，建立图4所示的尾传动系统等效扭振有限元模型，为便于分析，设置29个节点，关键节点位置见表3.将轴段离散化成n个微元轴段，有限元模型具有n个扭转自由度，其广义坐标为：

表3 尾传动系统当量化模型关键节点位置Table 3 Important nodes of idealized model of tail drive system

图4 尾传动系统等效扭转振动模型Fig.4 Equivalent torsional vibration model of tail drive system

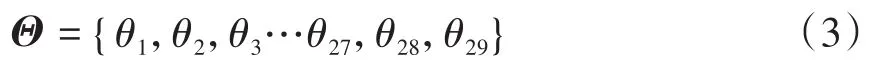
其中θi为第i微元处的扭转角位移.根据转子动力学理论，尾传动系统的扭振微分方程为：

其中，I为转动惯量矩阵，C为扭转阻尼矩阵，K为扭转刚度矩阵，Q为扭矩激励矩阵.

2 齿轮联结的相交轴转子系统扭振特性分析

2.1 扭振临界转速和扭振模态

直升机尾传动系统由三根传动轴和联结转轴的两级减速器组成，齿轮联结副使系统存在明显的啮合耦合，将系统级和各组成轴前五阶临界转速进行对比分析，如表4所示，转子系统的临界转速远远低于各组成轴.进而求解了尾传动系统的前10阶临界转速，如表5所示，分析发现，系统第1、2阶临界转速是由耦合作用产生，其余8阶系统级临界转速均源于各组成轴，其1、2阶扭振模态振型见图5，由图5可知，尾斜轴和尾桨轴的扭振幅值较大，需重点关注.

图5 前两阶扭振模态振型Fig.5 The first two torsional modes

表4 前5阶扭振临界转速对比Table 4 Comparison of critical speed of first 5 orders torsional vibration

表5 前10阶系统级临界转速Table 5 The first 10 orders critical speed of tail drive system

2.2 联结齿轮啮合刚度对扭振的影响研究

相交轴转子系统的激励源主要来自于联结齿轮副，齿轮副产生啮合激励将严重影响传动系统的工作状态，造成断轴、断齿等严重机械故障.

齿轮啮合过程中，由于参与轮齿啮合的齿对数是周期性变化的，因此，啮合过程中的刚度也是周期性变化的，轮齿的时变刚度可以看作啮合线方向的时变弹性元件产生周期性变化.这种因啮合刚度的时变性产生的动态啮合力并对齿轮传动系统进行激励的现象就是刚度激励.时变啮合刚度采用式（5）计算：

其中，kn（t）为时变啮合刚度，Fn（t）为法向动态啮合力，B为螺旋锥齿轮齿宽，δ（t）为齿面动态变形量.由于螺旋锥齿轮齿形复杂，传统解析法不适用于计算时变啮合刚度，因此使用Kisssoft软件计算时变啮合刚度，为简化计算，使用平均啮合刚度代替时变啮合刚度，同时忽略啮合阻尼对临界转速的影响.

基于已建立的有限元模型，研究相交轴转子系统的扭振响应，中、尾减平均啮合刚度为k1=1.6×106N/m，k2=3× 106N/m，

图6给出各节点处的扭振频谱，图中存在四个明显的共振转速，其数值分别对应于系统前四阶临界转速，各阶临界转速处不同节点的扭振角位移峰值存在显著差异.

图6 各节点扭振频谱图Fig.6 Spectrum of angular displacement at all nodes

进一步研究前四阶共振角位移随中、尾减齿轮副啮合刚度的变化规律.中减齿轮副啮合刚度k1取0.6×106N/m，依次递增 0.2×106N/m，至2.6×106N/m，尾减齿轮副啮合刚度k2=3.0×106N/m保持不变，分析关键节点17、18和29，即中减主动齿轮、中减从动齿轮和尾旋翼，扭转角位移随啮合刚度改变的变化规律，如图7所示.

图7 不同中减啮合刚度下的代表性节点各阶共振峰值17Fig.7 The resonant peaks of the representative nodes with different middle meshing stiffness

图7中，第1、2阶共振角位移对中减齿轮副啮合刚度变化响应丰富，中减啮合刚度取k1=1.0×106N/m，2.0×106N/m时，各节点一阶共振角位移出现极大值；中减啮合刚度取k1=1.4×106N/m时，节点18、29的二阶共振角位移出现极大值.由此说明，在系统结构设计时，上述中减啮合刚度值要尽量避免；在系统运行监测中，扭振的变大有可能是啮合刚度变化引发，为系统结构优化设计及运行维护提供依据.第四阶共振峰值对啮合刚度变化不敏感，但节点29的四阶共振峰值偏大.

尾减啮合刚度K2取2.0×106N/m，依次递增0.2×106N/m，至4.0×106N/m，中减齿轮副啮合刚度K1=1.6×106N/m保持不变.取关键节点23、24和29，即尾减主动齿轮、尾减从动齿轮和尾旋翼，分析扭转角位移随啮合刚度改变的变化规律，如图8所示.

图8中，第一、二、四阶共振扭转角位移对尾减齿轮副啮合刚度变化响应丰富，尾减啮合刚度K2=3.8×106N/m时，各节点一阶共振角位移出现极大值；尾减啮合刚度K2=3.0×106N/m时，各节点二阶共振角位移出现极大值；尾减啮合刚度K2=2.6×106N/m时，各节点四阶共振角位移出现极大值；在系统结构设计时，要尽量避免尾减的上述啮合刚度值.相较于图7，尾减齿轮副啮合刚度变化对各节点各阶共振的影响远大于中减齿轮副，在系统结构设计时，尾减的啮合刚度选用要更加谨慎.

图8 不同尾减啮合刚度下的代表性节点各阶共振峰值Fig.8 The resonance peaks of the representative nodes with different tail meshing stiffness

中、尾减齿轮副啮合刚度变化对各阶临界转速同样会产生影响，图9描述了系统前四阶临界转速随中、尾减齿轮副啮合刚度变化的规律.由图可知，第一、二阶临界转速对啮合刚度变化较敏感；尾减速器齿轮副啮合刚度的变化对临界转速的影响大于中减速器.

图9 系统前四阶临界转速随联结齿轮副变化趋势图Fig.9 The trend chart of the first four critical speed of the system with the coupling gear pair

2.3 联结齿轮转动惯量对系统扭振临界转速的影响

在尾传动系统中，两级减速器中的螺旋锥齿轮具有较大的转动惯量，对传动系统的扭振临界转速产生重要影响，将各部件的转动惯量按比例增减，令Ii=（δIp）kg·m4，（i=1，2，3，4，）分别代表中减主动轮（node17）、从 动 轮（node18）、尾 减 主 动 轮（node23）、从动轮（node24）；Ip为各部件的原始转动惯量，Ipc为各部件改变后的转动惯量；δ=（Ipc/Ip）×100%=25%，50%，75%，100%，125%，150%，175%，200%.为便于表现各阶临界转速随各部分（节点）转动惯量变化，以各δ值对应的临界转速与δ=100%时临界转速的差值为纵坐标，以表征转动惯量变化的δ值为横坐标，绘制尾传动系统各阶扭振临界转速对转动惯量变化的响应曲线.

由图10可知，尾传动系统扭振临界转速对不同部件转动惯量变化的敏感性不同，尾减速器主动轮（node23）对系统级临界转速的影响很小；尾传动系统不同阶临界转速对同一部件转动惯量变化的敏感性亦不相同.中减主动轮（node17）转动惯量的变化对尾传动系统第三、四、五阶临界转速影响较大.

图10 系统前四阶临界转速随转动惯量变化趋势图Fig.10 The trend chart of the first four critical rotational speeds of the system with the moment of inertia

3 结论

（1）本文提出一种基于Dyrobes的当量化建模方法建立齿轮联结相交轴转子系统的有限元模型，与已有研究成果对比验证了本方法的正确性.应用该方法建立了典型齿轮联结相交轴传动系统——直升机尾传动系统的有限元模型.

（2）基于已建立的直升机尾传动系统有限元模型，获得了传动系统扭转振动临界转速和模态振型；对比分析了各组成轴和传动系统的扭振临界转速，发现第1、2阶为系统派生临界转速，其余各阶源于各组成轴，并且轴系的扭振临界转速较各组成轴显著降低.

（3）中、尾减啮合刚度值与扭振的各阶角位移峰值存在映射关系，部分啮合刚度值会激发角位移极大值，保持尾减啮合刚度k2不变，取k1=1.0×106，1.4×106，2.0×106N/m时产生共振角位移极大值；保持中减啮合刚度k1不变，取k2=2.6×106，3.0× 106，3.8× 106N/m时产生共振角位移极大值；在系统结构设计及运行中应尽量避免上述啮合刚度值.中、尾减啮合刚度变化会引发系统临界转速的变化，尤其是第1、2阶临界转速.

（4）系统级临界转速对不同部件转动惯量改变的敏感性不同，中间减速器主动轮对系统级临界转速影响最大，尾减速器主动轮对系统级临界转速的影响最小；系统级各阶临界转速对同一部件转动惯量改变的敏感性也不同.