基于最大Lyapunov指数的行星齿轮传动系统混沌特性分析*

王靖岳 刘宁 王浩天

（1.沈阳理工大学汽车与交通学院，沈阳 110159）（2.重庆大学机械传动国家重点实验室，重庆 400044）（3.沈阳航空航天大学自动化学院，沈阳 110136）

引言

齿轮系统是应用广泛的动力传动装置，其振动和噪声问题也尤为突出，吸引了国内外大量学者对其非线性动力学特性进行研究［1-6］.

在现有研究文献中，很多学者采用相图和Poincaré截面结合的方法对系统进行定性分析，而采用Lyapunov指数可以对系统进行定量分析.李华等针对单对齿轮系统，利用Lyapunov指数来判别系统中的混沌吸引子，说明其可以作为判定齿轮系统运动状态的指标［7］.王晓笋等建立含侧隙的齿轮系统动力学模型，分析系统随侧隙变化的分岔图和最大Lyapunov指数图［8］.Hou等建立行星齿轮-转子系统的非线性分析模型，用分岔图和最大李雅普诺夫指数来说明系统的非线性响应［9］.向铃等建立了平移扭转耦合的齿轮系统动力学模型，基于Lyapunov指数分析系统随激励参数变化的动力学特性［10］.林何等建立含间隙和误差的齿轮非线性振动模型，采用Lyapunov指数和关联维数定量表述系统相空间吸引子的数值特性［11］.

对于齿轮系统混沌特性的研究，综合分析上述研究文献，多数为单对齿轮副的研究，而行星齿轮的模型研究很少，其模型构件较多，动力学特性也会更加复杂.因此，本文建立考虑啮合刚度、误差和齿隙等非线性因素的行星齿轮传动系统振动模型，采用数值方法求解，利用非线性分析方法，结合分岔图和最大李雅普诺夫指数（Largest Lyapunov Exponents，LLE）对行星齿轮系统的混沌特性进行分析.

1 系统动力学建模

如图1所示，定、动坐标系分别为onxnyn、Oxy，基于集中参数理论建立的行星齿轮扭转动力学模型，假定逆时针旋转为正，不考虑轴承间隙等非线性，每个行星轮的质量和转动惯量相同，同类型构件齿隙、综合啮合误差和阻尼比等参数也相同，啮合副的接触面简化为弹簧和阻尼器连接，c代表行星架、r代表齿圈、s代表太阳轮、n代表第n个行星轮（n=1，2，3…N），uc、ur、us、un分别表示上述构件的扭转位移.

图1 行星齿轮动力学模型Fig.1 Dynamics model of planetary gear

采用牛顿定律建立行星齿轮系统动力学微分方程：

式中，令j=s、c、r、n，i=sn、rn，sn为外啮合副；rn为内啮合副；Ij为转动惯量；rj为基圆半径；T1为输入扭矩；T2为输出扭矩.

通过石川公式计算齿轮副的啮合刚度［12］，时变啮合刚度随时间周期性变化，通过Fourier级数展开，取谐波基频部分：

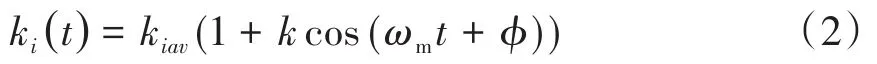
式中，kiav为平均啮合刚度；k为刚度系数；φ为刚度相位角；ωm为激励频率.

综合啮合误差主要为制造误差和安装误差，可以表示为正弦函数的形式：

式中，E为啮合误差幅值；γ为误差相位角.

齿轮副的啮合阻尼与啮合刚度相关，可以表示为：

齿侧间隙以啮合线方向为度量值，采用分段函数的形式，如图2所示，齿轮副间隙非线性位移函数可以表示为：

图2 齿侧间隙非线性函数Fig.2 Nonlinear function of backlash

为了消除刚体位移和使系统方程数目减少实现降维，引入内外啮合副的相对位移δ：

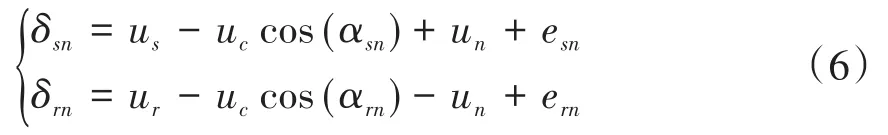
2 系统的分岔与混沌特性分析

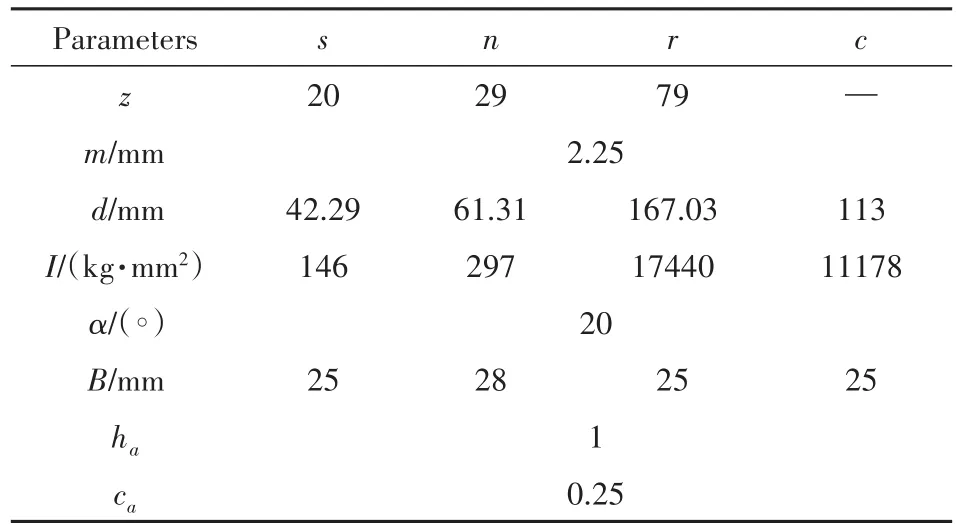
表1 行星齿轮系统基本参数[14]Table 1 Basic parameters of planetary gear system[14]

2.1 系统随激励频变化的分岔与混沌特性

以无量纲激励频率Ω为变化参数，得到系统的分岔图和LLE图，如图3所示.从图3中可以看出，随着Ω的增加，系统首先为周期运动，在此区域伴随有短暂阵发性混沌，对应LLE图中有正值区域，然后系统完全进入混沌运动，之后系统再次进入周期运动，途径为逆倍化分岔，在高频区域的周期运动发生倍化分岔，最后稳定在1周期运动，同时在此期间也夹杂几处混沌运动.当Ω在［0，0.76］区间时，系统为1周期运动；当Ω增加到0.78时，系统发生Hopf分岔进入2周期运动；当Ω增加到0.88时，系统为4周期运动，之后系统暂时经激变进入阵发性混沌，对应LLE值为正；当Ω在［1.04，1.14］区间时，系统为2周期运动，状态改变途径为跳跃激变；当Ω在［1.14，1.52］区间时，系统为混沌运动状态，LLE值为正，呈先增后减趋势；当Ω在［1.52，2.18］区间时，系统状态为混沌运动→4周期运动→2周期运动→1周期运动；当Ω在［2.18，2.28］区间时，系统发生跳跃激变，由4周期跳跃为2周期；当Ω在［2.28，2.7］区间时，系统主要为8周期运动，伴随短暂的阵发性混沌，对应LLE图在正值区域有几处尖峰；当Ω在［2.7，2.94］区间时，系统为2周期运动；当Ω在［2.94，4］区间时，系统锁相为1周期运动.

图3 系统随Ω变化的分岔图和LLE图Fig.3 Bifurcation diagram and LLE diagram of the system withΩ

2.2 系统随阻尼比变化的分岔与混沌特性

取激励频率Ω=1，以阻尼比ζ为变化参数，得到系统的分岔图和LLE图，如图4所示.从图4可以看出，随着ζ的增加，系统开始的混沌特性明显，在状态临界点处系统状态复杂，最后系统由逆倍化分岔进入周期运动，符合增大阻尼可以使系统摆脱混沌，从而使系统趋于稳定.当ζ在［0.07，0.093］区间时，系统主要为混沌运动，同时伴有阵发性混沌和周期窗口，对应的LLE值在正负区域之间变化；当ζ在［0.093，0.106］区间时，系统经逆倍化分岔进入4周期运动，LLE值为负，呈减小趋势；当ζ继续增加到0.108时，系统最后稳定在2周期运动.

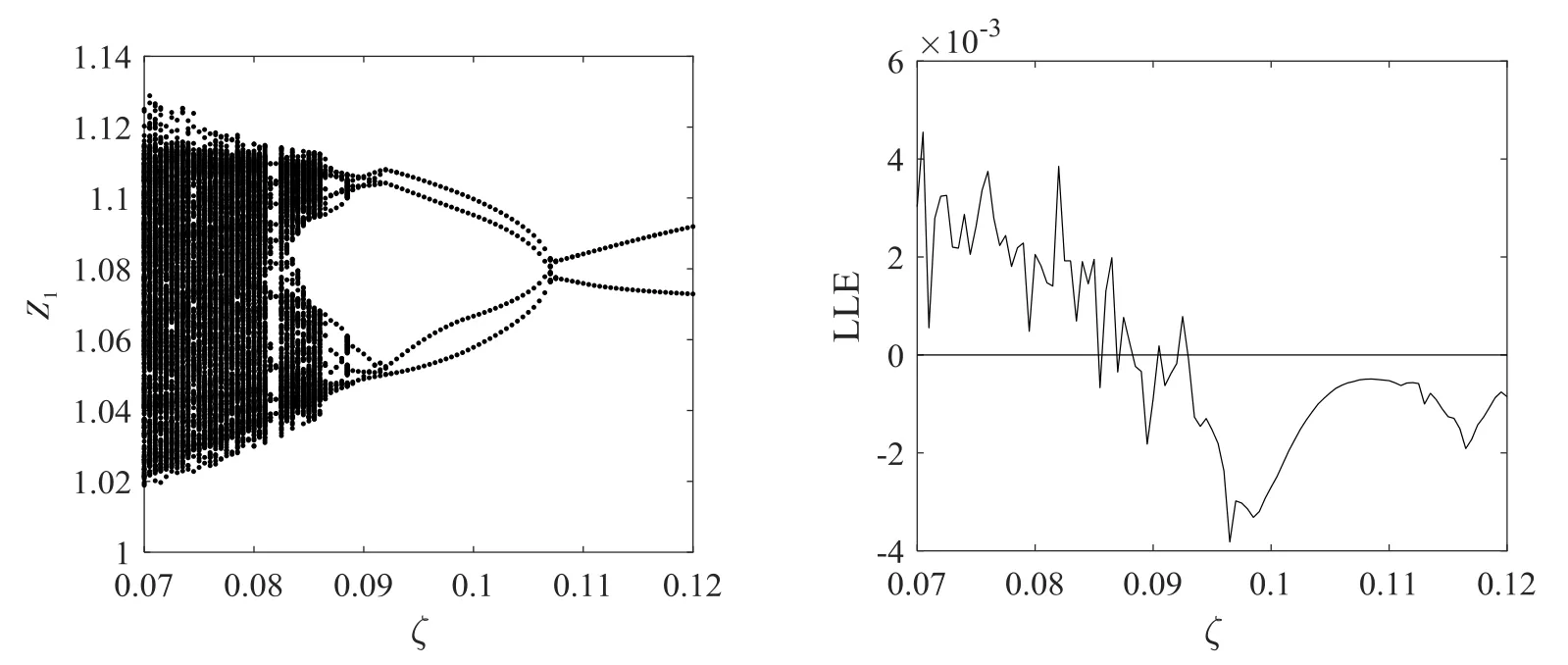
图4 系统随ζ变化的分岔图和LLE图Fig 4 Bifurcation diagram and LLE diagram of the system withζ

2.3 系统随综合误差幅值变化的分岔与混沌特性

取Ω=1，以误差幅值E为变化参数，得到系统的分岔图和LLE图，如图5所示.从图5可以看出，随着E的增加，系统开始为单周期运动，之后为逐渐倍化分岔多倍周期运动，最后进入混沌运动，同时伴有狭窄的周期或拟周期窗口.当E在［0，1.4］区间时，系统为1周期运动，LLE值为负；当E在［1.4，2.04］区间时，系统为2周期运动，在此区间，当E为1.5时，发生跳跃激变；当E在［2.04，2.06］区间时，系统暂时为拟2周期运动，LLE值为0；当E在［2.08，2.22］区间时，系统为多倍周期运动分岔行为，6周期运动→12周期运动→24周期运动；当E在［2.24，3］区间时，系统混沌特性明显，同时混沌区域中周期窗口不明显，说明系统已处于不稳定状态，符合实际误差变大，系统混沌振动特性也随之增强.

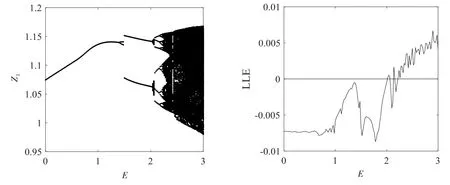
图5 系统随E变化的分岔图和LLE图Fig.5 Bifurcation diagram and LLE diagram of the system withE

2.4 系统随荷载变化的分岔与混沌特性

取激励频率Ω=1，以荷载T为变化参数，得到系统的分岔图和LLE图，如图6所示.从图6中可以看出，随着T的增加，系统开始的混沌状态明显，分岔行为模糊，状态改变为跳跃激变和逆倍化分岔，系统的周期运动区间也存在两处不稳定的混沌区域，LLE图中为两处尖峰，最后系统稳定在单周期运动.当T在［0，70］区间时，系统为混沌运动状态，LLE值为正；当T增加到75时，系统由混沌运动逆倍化分岔为2周期运动，对应LLE值由正变负；当T增加到90时，系统跳跃激变为4周期运动，当T在［90，120］区间时，系统主要为4周期运动，伴有阵发性混沌.当T在［125，250］区间时，系统为周期运动，由4周期运动→2周期运动→1周期运动，状态改变途径为逆倍化分岔.

图6 系统随T变化的分岔图和LLE图Fig 6 Bifurcation diagram and LLE diagram of the system withT

2.5 系统随齿隙变化的分岔与混沌特性

取激励频率Ω=1，以齿隙b为变化参数，得到系统的分岔图和LLE图，如图7所示.从图7中可以看出，随着b的增加，系统首先为周期运动，同时发生Hopf分岔，最后经倍化分岔进入混沌运动，在混沌区间伴有两段狭窄的周期窗口，对应LLE在负值区域有两处尖峰.当b在［0，0.38］区间时，系统为1周期运动，LLE值为负；当b增加到0.4时，系统经Hopf分岔进入2周期运动；当b在［1.26，1.52］区间时，系统有两个混沌带，伴有周期运动和拟周期运动，对应LLE值在正负区域变化；当b在［1.54，1.62］区间时，系统为多倍周期运动，分岔途径为倍化分岔；当b增加到1.62时，系统经倍化分岔进入混沌运动，对应LLE值为正.

图7 系统随b变化的分岔图和LLE图Fig.7 Bifurcation diagram and LLE diagram of the system withb

2.6 系统随刚度幅值变化的分岔与混沌特性

取激励频率Ω=1，以刚度幅值k为变化参数，得到系统的分岔图和LLE图，如图8所示.从图8中可以看出，随着k的增加，系统的分岔行为简单，由单周期运动经倍化分岔进入混沌运动.当k在［0，0.35］区间时，系统为1周期运动；当 k在［0.35，0.81］区间时，系统为2周期运动，对应的LLE值为负；当k在［0.81，1］区间时，系统为混沌运动，对应的LLE在正值区域变化且逐渐增加，表明系统混沌程度增大.

图8 系统随k变化的分岔图和LLE图Fig.8 Bifurcation diagram and LLE diagram of the system withk

3 结论

建立考虑齿隙、时变啮合刚度和综合啮合误差等多种非线性因素的行星齿轮扭转动力学振动模型，采用Runge-Kutta数值方法，研究了系统随激励频率、阻尼比、综合误差幅值、载荷、齿隙和刚度幅值变化时的分岔和混沌特性.

（1）随着激励频率的增加，系统分岔行为丰富，运动状态在单周期运动、多倍周期和混沌运动之间多次变化，途径为跳跃激变、倍化分岔和逆倍化分岔，LLE在正值区域减小.

（2）随着阻尼比的增加，分岔行为明显，系统开始混沌特性明显，最后经逆倍化分岔由混沌运动进入周期运动，对应的LLE值由正变负.

（3）随着综合误差幅值的增加，系统分岔行为丰富，经倍化分岔由单周期运动逐渐变为多倍周期运动，最后倍化分岔进入混沌运动，LLE值在正值区域逐渐增加.

（4）随着荷载的增加，系统分岔行为模糊，系统由混沌运动经跳跃激变和逆倍化进入周期运动，在周期运动区域，最后经逆倍化分岔锁相为稳定的1周期运动，LLE值总体趋势减小.

（5）随着齿隙的增加，系统分岔行为变得复杂，主要集中在混沌区域中的周期窗口，最后，经倍化分岔由周期运动进入混沌运动.LLE值先逐渐增加，最后，在正值区域围绕0.005上下波动.

（6）随着刚度幅值的增加，系统分岔行为简单，由周期运动经倍化分岔进入混沌运动，LLE值整体趋势增加.