时滞反馈与多频激励联合作用下Duffing振子的快慢动力学*

王东梅 余跃† 张正娣

（1.南通大学理学院，南通，226019）（2.江苏大学理学院，镇江，212013）

引言

各种实际的非线性问题中往往涉及时滞的影响［1-4］.具体而言，其产生根源往往来自于自然界、工程技术和社会生活中普遍存在的信号传输时间延迟、转换速度过程和记忆效应等［5.6］.例如，远距离通讯信号的传递，控制系统中信号反馈存在的时间差，车辆上用到的半主动悬架系统中不可避免的延迟，测量信号从传感器至控制计算机的传输时滞，作动器引起的响应时滞和建立控制需要的时间，以及系统物理和化学性质导致的时滞等［7，8］.此外，时滞动力系统也是描述金属切削过程颤振、生物系统演化等问题的重要数学模型［9，10］.由于时滞动力系统的广泛适用，讨论时滞因素及其耦合模式在内的多因素联合所导致的多级分岔，以及伴随的复杂动力学行为分析，不仅可以解决工程应用学科中遇见的一些重要实际技术问题，还将同时推动时滞动力系统自身理论的丰富与发展［11，12］.

许多重要工程实际问题中的复杂振动模式还往往需要考虑不同形式的激励，如周期外激、参数激励以及混合激励.激励因素对单自由度或多自由度非线性系统的非线性振动、分岔和混沌动力学行为将会产生显著影响.例如，张伟等［13］研究了参数激励和外激励联合作用下薄板的非线性动力学，给出一类四边简支矩形薄板系统发生周期运动-概周期-混沌的动力学演化规律.邓子辰等［14］考虑两种激励下的复杂结构，模拟了碳纳米管的振动，研究了碳纳米管的轴向动态屈曲特性.彭志科等［15］则建立了多级齿轮箱系统在传动误差、时变啮合刚度和激励联合作用下的参数模型，讨论了系统在随机激励作用下的动力特性.王如彬等［16］则分析了外激励如何影响神经网络神经元的数量以及同步转迁过程，为进一步研究大脑皮质深层复杂动力学创造了条件.这些文献均系统分析了不同激励因素对系统动力特性的影响.

含时滞反馈的Duffing振子可用于描述多种工程系统，具有非常广泛的应用，许多力学与数学工作者都对此做过深入研究［17-19］.Maccari［20］等人利用时滞位移和速度反馈控制法研究了Duffing振子的非线性振动响应.胡海岩、王在华等［21］则研究了Duffing振子中的延迟AD（加速度导数）控制器设计以及分岔控制.杨韶普、申永军［22］等人研究了含时滞分数阶Duffing振子动力学特性，分析了反馈系数、分数阶非线性刚度系数、分岔点位置、周期解的稳定性、周期解的存在范围、零解的稳定性和稳定切换等因素对复杂动力行为的影响.徐鉴、孙秀婷等［23］选取反馈时滞及其增益作为控制参数，讨论了基于时滞Duffing方程的非线性隔振器设计.徐伟和孙中奎等［24］考虑了 Van der Pol-Mathieu-Duffing系统的混沌响应，给出了系统通向混沌的噪声阈值条件.孙剑桥等［25］研究了一类慢变激励作用下的Duffing振子的混沌动力学，讨论了几类新型混沌响应.许勇等人［26］则用数值方法研究了双稳态Duffing系统中的Levy噪声因素，以及因此产生的相变过程和通过时间.张丽等［27］研究了Van der Pol-Duffing系统的全局Hopf分岔特性和转迁机制.

本文在上述结果的研究基础上，考虑线性时滞位移反馈与多频激励联合作用的负刚度Duffing振子，

其中τ>0为时滞量，A>0表示正反馈增益，反之表示负反馈，而f1和f2为激励振幅，ω1和ω2是激励频率.当受迫振动激励频率接近系统固有频率，即多频激励的频率量级为O（1）时的系统动力学已经有诸多学者做了相关研究［28-30］.当激励频率远小于系统固有频率并且系统含有时滞因素时，系统将演化为时滞系统快慢动力学问题［31，32］.多频激励和时滞反馈联合作用下的非线性振荡以及动力学分析，对于理解快慢变时滞系统与不变流形方法有关的处理技巧，分析时滞及其增益系数对状态变量在不同时间尺度下的运动规律，进而探讨多稳态解共存下的复杂动力学有重要的理论意义和应用价值［33-36］.

1 时滞引起平衡点稳定性切换

当系统（1）中时滞τ=0时，系统（1）为多频激励下无时滞Duffing振子的动力学问题，已经有许多平凡的结果.进一步，当f1=f2=0时，自治系统的动力学行为较为简单，即存在平凡平衡点E0（0，0）和对称的非平凡平衡点E±（± 1，0）.这些平衡点的稳定性由相应特征方程根的情况决定.例如，E0有特征根-1.618和0.618，即为不稳定鞍点.而E±（± 1，0）的特征根为-0.5± 1.3229i，即焦点形式的双稳平衡态.

以下讨论τ>0时，时滞位移反馈对系统平衡点E0局部分岔行为的影响，对应的特征方程为

假设λ=a±ib，其中实数a，b>0表示实部和虚部.当a=0，系统发生Hopf分岔的必要条件是：

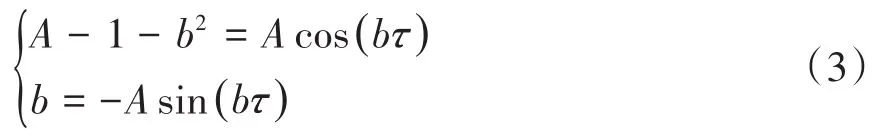
对式（3）进行平方和运算可得b4+（3-2A）b2-2A+1=0，即

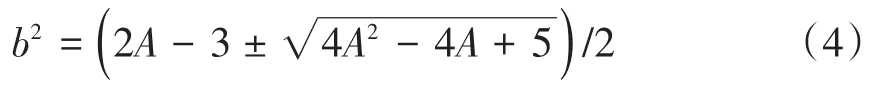
要使得式（4）解集成立，增益系数需要满足A>1/2，此时得到虚部b的进一步表达式

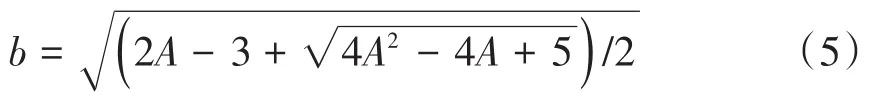
根据Hopf分岔定理，此时平衡点E0发生Hopf分岔的临界时滞条件是

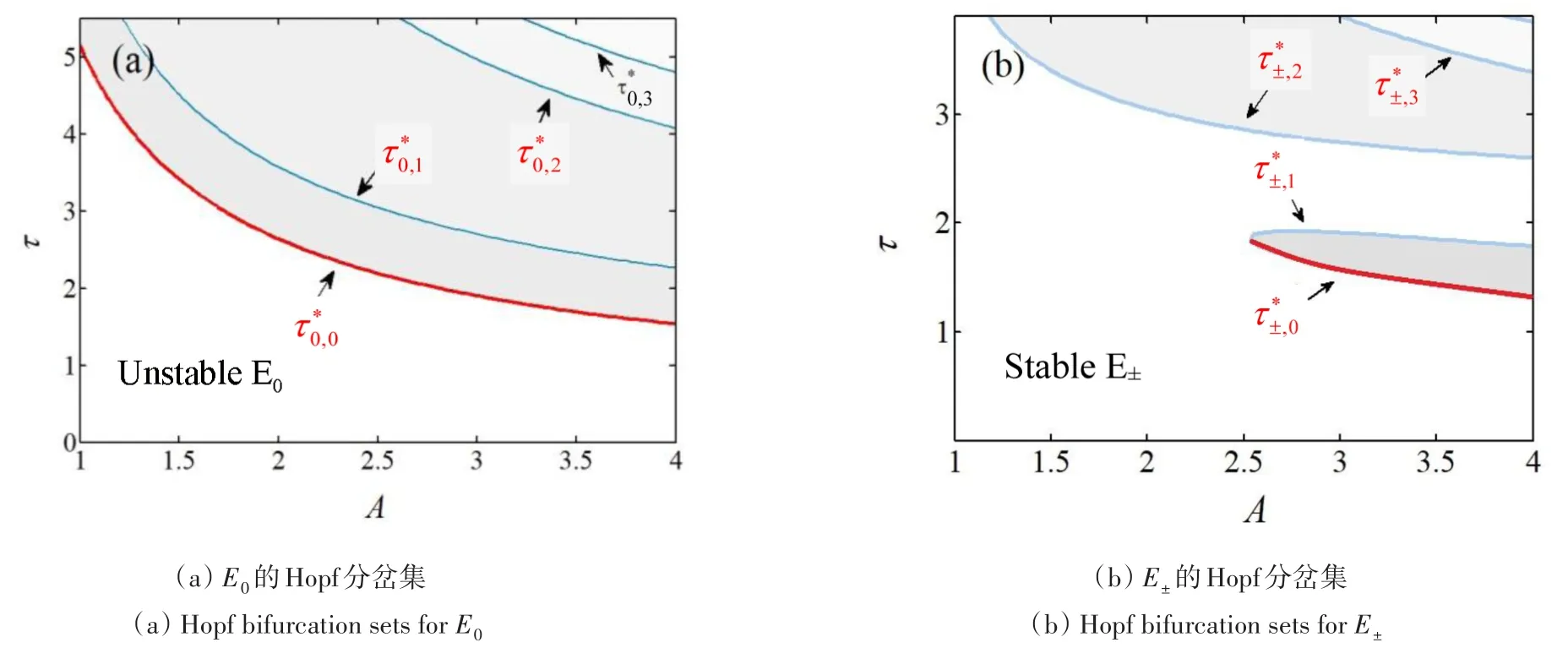
图1 系统（1）在f1=f2=0时平衡点受时滞量和反馈增益影响的分岔集Fig.1 Curve of system bifurcation on the plane of（A，τ）equilibrium points forf1=f2=0

下面考虑非平凡平衡点E±处的Hopf分岔，此时对应的特征方程为

同样将特征根λ=bi，b>0代入方程（7），得到E±发生Hopf分岔的条件是

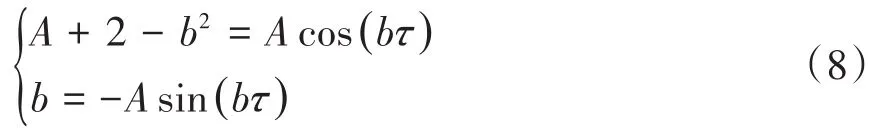
对式（8）进行平方和运算可得b4-（3+2A）b2+4A+4=0，解得

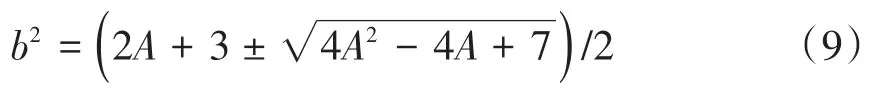
当时滞增益系数满足A>0，进一步得到虚部b的表达式

根据Hopf分岔理论，将公式（10）代入（6），得到平衡点E±发生Hopf分岔的临界时滞

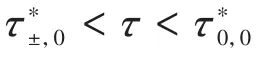
图2 系统（1）A=3.5，f1=f2=0时共存吸引子Fig.2 Phase portraits of system（1）forA=3.5，f1=f2=0

2 多频激励分析方法

多频激励下的快慢变流形已经有了相关工作［37，38］.这里我们简要介绍一下处理技巧，基于棣莫弗公式可得

这里m是不超过整数n的最大偶数.基于公式（12）可以列举出诸如n=2和n=3的简单例子，即cos（2x）=2cos2x-1，cos（3x）=4cos3x-3cosx.不失一般性，本文考虑混合激励频率之间满足ω1：ω2=1：2共振关系.假设β=cos（ω1t），可得cos（ω2t）=2β2-1，系统（1）关于快变量x与慢变量β的流形表示为，

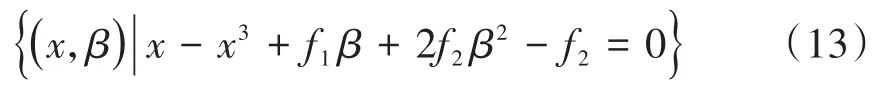
快慢变流形上的局部极值点，即二组Fold分岔点可以根据式（13）计算得到.设二元函数F（x，β）=x-x3+f1β+2f2β2-f2，由隐函数公式可知，

由公式（15）可知Fold分岔不受时滞增益以及时滞量大小的影响，但会受到激励幅值的影响.可以通过改变多频激励的幅值f1和f2，调节快慢变流形，使得局部极值点发生位移，进而改变系统的振荡特性.本文进一步选取两组激励幅值f1=1和f2=±1.5，分别生成开口朝左和右的多弯曲状流形，如图3（a）和3（b）所示，其中单箭头表示流形上吸引子与排斥子的分布情况，而局部极值点Fi（i=1，2，3，4）为流形上的Fold分岔点，此处系统的动力特性将会因为Fold分岔发生转迁，产生不同稳态分支上的大幅跳跃振荡行为.当f1=1，f2=1.5时，图3（a）中的Fold分岔点坐标为 F1（-0.5774，0.6433），F2（0.5774，0.4654）， F3（-0.5774，-0.9767） 和F4（0.5774，-0.7987）.类似的，当激励值f1=1，f2=-1.5时，图3（b）中的Fold分岔点坐标分别为F1（ -0.5774，0.7987） ，F2（0.5774，0.9767） ，F3（-0.5774，-0.4654），F4（0.5774，-0.6433）.

图3 系统（1）在外激频率共振比为1：2下的多曲形流形Fig.3 Multi-curve-shaped manifolds with excited resonance frequency ratio1：2of system（1）

3 复杂动力学行为分析

通过上述分析可知，在不同的参数条件下，系统均会因为时滞反馈和多频激励因素呈现出不同的分岔特性，这些特性会对系统最终的复杂行为产生影响.由于激励频率与系统自身固有频率之间存在着量级差距，系统将会产生不同尺度耦合效应，表现为大幅振荡与微幅振荡交替出现的动力学行为，同时受到时滞反馈的影响.下面，选取系统（1）激励幅值f1=1和f2=±1.5，并进一步固定激励频率ω1=0.01和ω2=0.02，这里β=cos（0.01t），基于多曲状快慢变流形讨论系统的不同模式振荡.

3.1 反馈增益系数A<1/2的周期振荡

显然，在反馈增益A<1/2条件下，负刚度系统的两个非平凡平衡点呈现稳定的焦点性态，快慢耦合效应不会随时滞量的变化而发生明显变化，系统特性始终表现为围绕多曲状流形上的大幅跳跃与微幅振荡耦合的周期振荡行为.图4和图5给出了系统（1）在时滞反馈增益A=-1和时滞量τ=1，激励幅值分别为f1=1和f2=±1.5时的不同平面上的相轨，并通过在平面（x，β）嵌入多曲状流形揭示出其动力学转迁过程.可以看出，此时系统轨迹在焦点吸引子之间发生大幅跳跃，出现分布在慢变流形上围绕两侧不同平衡点处衰减的微幅振荡与大幅振荡之间的联接.

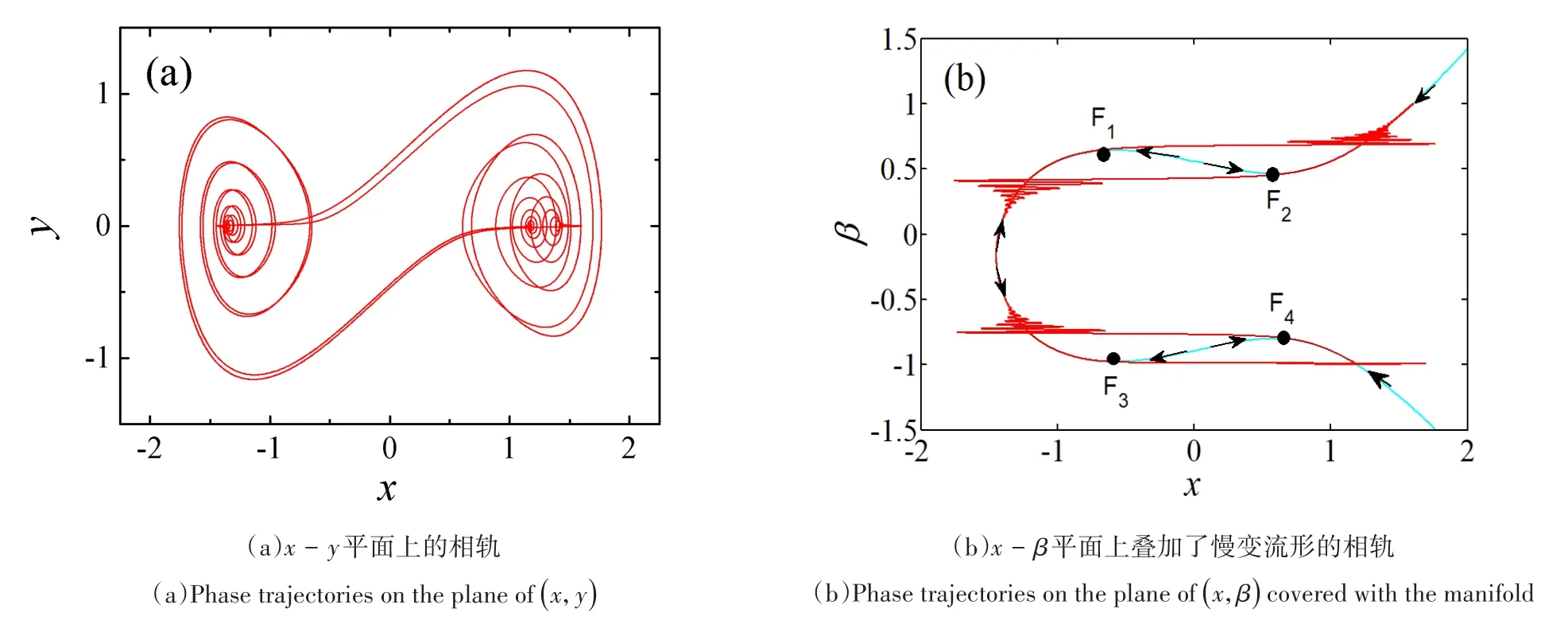
图4 A=-1，τ=1，幅值f1=1和f2=1.5时的相图Fig.4 The phase trajectories of system（1）forA=-1，τ=1，f1=1andf2=1.5

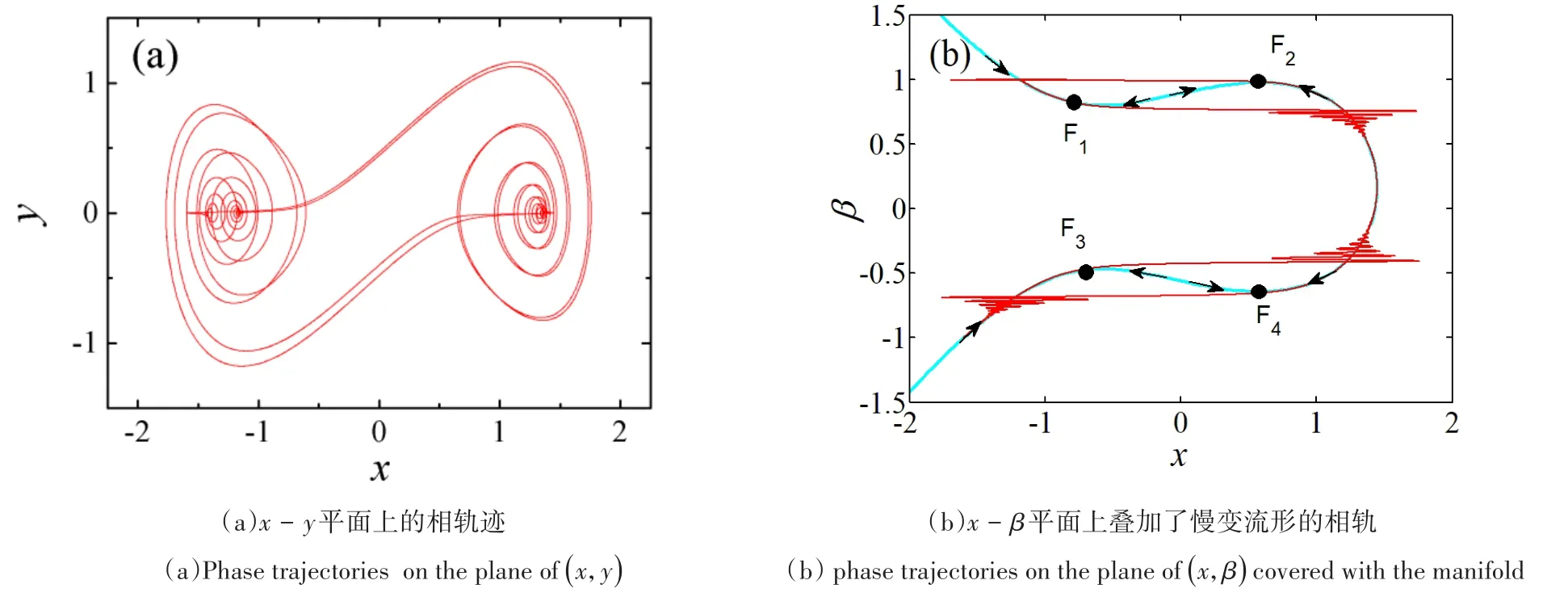
图5 A=-1，τ=1，幅值f1=1和f2=-1.5时的相图Fig.5 The phase trajectories of system（1）forA=-1，τ=1，f1=1andf2=-1.5

此类动力学行为中，以快慢变流形上的局部极值点，即Fold分岔点Fi，i=1，2，3，4作为分界点，联接快慢过程.不同的稳态解（焦点吸引子）之间的跳跃过程，对应相对剧烈的大幅振荡，即激发态.而围绕吸引子逐步趋向平衡点的过程，对应相对平缓的微幅振荡，即沉寂态.不同振荡方式之间的分岔联接方式，受时滞影响不大，始终适用于慢变流形之上，在不同的稳态解（稳定的焦点）之间转迁.

下面，我们以外激励幅值为f1=1，f2=1.5时的情况为例，如图4所示，分析系统轨迹在一个周期内的转迁过程.假定系统轨迹从F1点向右侧出发，在经过Fold分岔点F1时，系统沿着左侧平衡态分支E-的运动失稳（F1也是稳定流形与不稳定流形的分界点），系统轨迹发生跃迁，即朝向右侧平衡点E+大幅跳跃.此后，系统围绕稳定的平衡点E+振荡，由于E+表现成稳定的焦点，此时的振荡幅值持续衰减，直到慢变量β到达极大值β=1处.此后随着β减小，轨迹沿着平衡点曲线折回，开始远离平衡点E+而向左运动，直到运动到第二个Fold分岔点F2处.经过F2点后，轨线运动再一次失稳，而向左侧平衡点E-发生大幅跃迁，此后受到E-焦点性态的影响，系统的振荡幅值逐渐衰减，直到贴近平衡点曲线上的稳定流形部分，此时慢变量β进一步减小.

随着慢变量减小，系统沿着平衡点曲线到达第三个Fold分岔点F3，随后围绕左侧平衡点分支E-的轨迹第三次失去稳定性，在经过F3后发生再一次大幅跳跃，使得系统轨迹回到右侧稳定平衡点E+的吸引域中.此后，轨迹沿着稳定的平衡点E+运动，慢变量β到达其变化最小值β=-1处.接着，系统轨迹沿着平衡点曲线折回，向左侧运动直到Fold分岔点F4.然后，右侧的稳定平衡点分支消失，系统重新回到左侧平衡点E-的吸引域中，系统轨线经过第四次大幅跳跃靠近平衡点E-，E-呈现焦点特性，因此系统振幅衰减，直至贴近平衡点曲线上的稳定流形部分.最后，轨线再一次回到初始点F1，完成整个振荡周期.值得指出的是，一个完整的振荡周期内，系统围绕着稳定流形与不稳定流形产生了四次大幅跃迁，每次转迁后轨线围绕新的平衡点振荡，幅值衰减.

图4与图5的动力学特性的区别在于由于激励幅值的改变，导致慢变流形上稳定态的分布位置发生变化，系统动力特性也随之改变.但是，四个Fold分岔点（局部极值点）仍然将系统的轨迹划分为快慢分离的四个部分，分别受稳定平衡点吸引，围绕平衡点之间跳跃转迁.虽然，系统周期稳态解的产生机制保持不变，但影响了慢变流形的走向，还使得相关动力学轨迹变化明显.这使得此类张弛振荡在向量场的分布出现了更多可能.随着多频激励参数的继续变化，系统的此类转迁行为会产生更加丰富的周期振荡行为.必须说明的是，无论如何改变时滞量，此种快慢联接的定性性质依然保持不变，依旧是平衡点数量的改变导致的.这种情况下，激励幅值对于调节时滞振子快慢动力学行为是更好的手段，恰当选择激励幅值有益于产生更为丰富的非线性现象.

3.2 增益系数A>1/2，时滞增大时的振荡机制

在时滞反馈增益A>1/2条件下，随着时滞量的增加，系统局部稳定的平衡点可以经过Hopf分岔生成稳定的极限环.此时，系统的动力学特性将发生明显的改变，将表现为围绕多曲状流形上的快慢变耦合的周期振荡.图6和图7分别给出了系统（1）在时滞反馈A=3.5和τ=1.5，激励幅值分别为f1=1和f2=±1.5时的相图，并通过嵌入多弯曲状流形揭示出其动力学转迁过程.

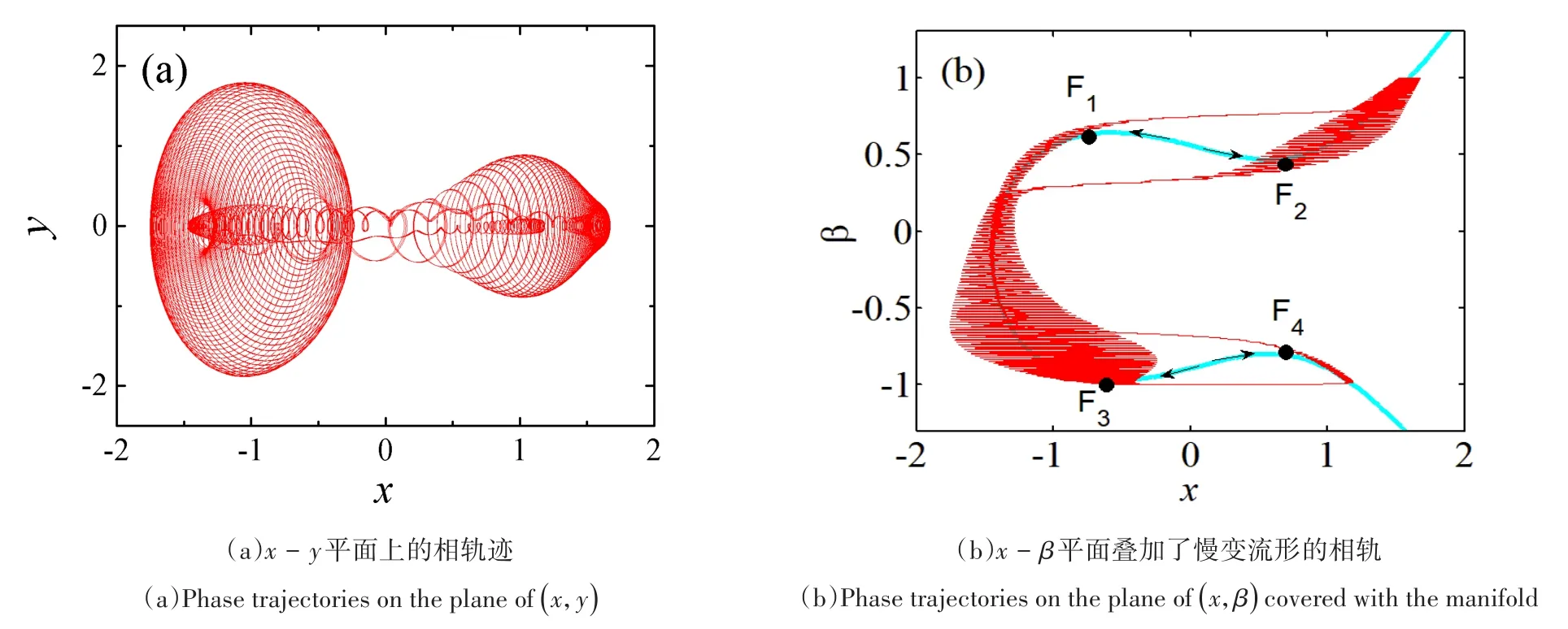
图6 A=3.5，τ=1.5，幅值f1=1和f2=1.5时的相图Fig.6 The phase trajectories of system（1）forA=3.5，τ=1.5，f1=1andf2=1.5

图7 A=3.5，τ=1.5，幅值f1=1和f2=-1.5时的相图Fig.7 The phase trajectories of system（1）forA=3.5，τ=1.5，f1=1andf2=-1.5

当A>1/2，且时滞满足Hopf分岔发生的临界条件，与之前激发态是围绕平衡点的运动模式不同，由于受时滞影响而产生极限环振荡，即此时系统激发态部分的极限环特征十分明显.随着控制参数β在慢变流形上变化，系统动力特性的转迁既有围绕平衡点收敛，又有围绕局部稳定极限环的周期振荡.多曲状流形上稳定与不稳定流形的交替出现，诱发系统的复杂振荡依旧具有明显的跳跃，即由稳定分支跨越到其它稳定分支，同时包含有局部极限环振荡，这导致（x，β）相平面上可以观察到密集的局部簇发行为.

以外激励幅值为f1=1，f2=1.5为例，系统的稳定平衡点分布在左侧的弧段和右侧开口的二弧段上.如图6所示，越接近左侧的慢变流形，系统动力特性停留的时间更长，表现为极限环振荡幅值越大，且振动频率也接近Hopf分岔的理论值，即特征值虚部数值.当极限环轨道运动到稳定和不稳定流形的分界点处，受到不稳定流形的排斥，系统特性发生变化，此时系统轨迹发生大幅跳跃到达另外一侧的稳定分支.接着，受到时滞诱发的Hopf分岔作用，产生围绕平衡点的稳定局部极限环振荡.上述转迁过程往复进行，完成一个完整周期的复杂振荡行为.

如图6（b）所示，慢变流形开口向右，分析系统轨迹在一个周期内的转迁过程.假定系统轨迹从F1点向右侧出发，在经过Fold分岔点F1时，系统沿着左侧平衡态分支E-的运动失稳（F1也是稳定流形与不稳定流形的分界点），系统轨迹发生跃迁，即朝向右侧平衡点E+大幅跳跃.此后，系统围绕稳定的平衡点E+振荡，直到慢变量β到达极大值β=1处.由于E+附近因时滞产生Hopf分岔而产生稳定的围绕E+的极限环振荡，此时极限环的振荡幅值逐渐增大.此后随着β减小，轨迹沿着平衡点曲线折回.系统轨迹继续以极限环形式振荡，直到运动到第二个Fold分岔点F2处，右侧稳定流形消失，使得系统轨迹产生大幅跃迁，回到左侧稳定分支.即系统运动失去稳定性，轨线围绕左侧平衡点E-运动.此后随着慢变量减小，系统轨迹向下运动.同时，受到E-处时滞诱导的Hopf分岔影响，系统围绕E-的极限环振荡，幅值逐渐增大，直到到达新的稳定流形与不稳定流形的临界点F3处.系统轨迹到达F3处后，围绕左侧平衡点分支E-的极限环振荡再次失去稳定性，即表现为过F3后发生第三次大幅跳跃，使得系统轨迹回到右侧稳定平衡点E+的吸引域中.此后，轨迹沿着稳定的平衡点E+运动，慢变量β到达其变化最小值β=-1处.这个阶段的系统轨迹受到时滞作用，依旧呈现极限环振荡，但是极限环较小，振荡幅值也随之减小，直到轨迹沿着平衡点曲线折回.

随后，系统轨迹向上折回，受时滞影响沿着平衡点曲线微幅振荡运动到F4处.随着右侧稳定分支消失，系统产生第四次大幅跳跃，回到左侧的稳定流形上，围绕平衡点E-振荡.此时轨迹受到时滞作用，依旧呈现极限环振荡，体现在轨线围绕左侧分支仍然出现环状振荡.最后，轨线围绕左侧极限环微幅振荡，并持续向上运动回到初始点F1，完成整个振荡周期.值得指出的是，一个完整的振荡周期内，系统围绕着稳定流形与不稳定流形产生了四次大幅转迁.由于受到时滞的影响，轨线在一段朝向E±的暂态过程后，都会因Hopf分岔产生围绕两侧平衡点E±的极限环振荡.

图7则揭示了激励幅值f2=-1.5的动力学转迁特性，此时慢变流形的开口朝左侧.密集的极限环振荡更多的围绕在右侧平衡点E+所在区域，当系统轨线沿着局部极限环振荡经过临界点F2，4处，原有稳定分支失稳，开始受到不稳定的流形排斥，系统轨迹大幅跳跃到左侧.与之对应的是，系统在左侧平衡点E-所在区域作极限环振荡，当经过临界点F1，3处，受到不稳定流形的排斥，系统轨迹通过大幅跳跃回到了右侧，继续呈极限环振荡.上述变化趋势，与图6的趋势是恰好相反的过程.通过激励幅值的调节可以调节快慢流形的动态特性，从而调谐这类张弛振荡.这类多频激励和时滞反馈联合作用下的动力学行为，将在电路设计，激光通信，信号检测等领域带来许多潜在的应用.

4 结论

研究了时滞反馈与多频激励联合作用下Duffing振子的非线性动力学.通过求解时滞反馈振子的特征方程，讨论了特征根分布，获得了Hopf分岔发生的条件，并在反馈增益强度和时滞平面上给出了分岔区域.通过棣莫弗公式，对系统进行快慢流形解耦，得到了稳定和不稳定流形的多弯曲联接特性.结合数值计算，给出了诸如焦点/焦点型混合振荡，局部极限环/局部极限环的混合振荡等复杂动力学现象.结果表明，含时滞反馈的非线性系统，其快慢动力学行为有着更特殊的规律性，会受到更多因素作用.当反馈增益A<1/2时，调节时滞量不会改变系统振荡的转迁机理，轨线始终围绕着稳定平衡点吸引子往复跳跃.随着反馈增益A>1/2和时滞量的增大，系统出现极限环吸引子之间的跃迁特性.上述动力学行为对激励系数和时滞反馈十分敏感依赖.本文的研究结果对通过时滞反馈和多频激励来增强或抑制快慢动力学行为，产生更为新颖的快慢振荡模式具有较强的理论意义和参考价值.