车辆系统的非线性行驶动力学响应*

韩彦伟 张子建

（1.河南科技大学土木工程学院，洛阳 471023）（2.南京航空航天大学航天学院，南京 210016）

引言

随着汽车、高铁、轨道交通等车辆系统的运行速度大幅提高，导致行驶车辆的非线性振动演化与机理问题引起国内外学者的广泛关注.在车辆的道路行驶过程中，由于路面不平会引起车体的振动，如垂向振动、前后俯仰振动及左右摇摆振动等，这些振动会降低车辆的操作稳定性、乘坐舒适性、驾驶的安全性，增加油耗、减少使用寿命.当车辆高速行驶时，车体的振动越加强烈，导致各项性能愈来愈差.为解决这些问题，一种方法是通过提升路面的平顺度，从而减少路面激励输入；另一种方法是在轮胎与车身之间安装弹簧阻尼悬架系统，实现对路面激励的隔离，从而实现减震和降噪.其中非线性悬架模型研究与应用是非常重要和有效的方法，成为了车辆工程领域的学术焦点之一.

非线性车辆悬架系统的复杂非线性振动特性得到许多学者的广泛关注.李韶华［1］研究了具有非线性刚度和Bingham阻尼的单自由度悬架系统亚谐共振和奇异性.孙蓓蓓［2］分析了橡胶悬架两自由度立方非线性刚度车辆系统的幅频响应、转迁集及分岔等非线性动力学特性.高大威［3］考虑双频激励作用下的三次非线性刚度与阻尼单自由度悬架系统的混沌运动及混沌追踪控制方法.朱峰［4］给出了五次阻尼非线单自由度非线性系统的混沌特性及其对稳定性的影响.丁继斌［5］利用AMEsim仿真方法研究了油气悬架模型两自由度车辆系统的亚谐波和超谐波共振特性.牛治东［6］得到了随机激励作用下迟滞非线性单自由度悬架系统的混沌振动及混沌振动临界条件.

综上所述，现有研究多集中在单、两自由度系统的垂直方向振动特性，而对垂向与俯仰方向的非线性耦合振动较少涉及［7-9］.另外，立方刚度非线性与立方阻尼非线性均是对原系统的近似逼近，无法实现对非线性车辆系统的精确描述.因此，本文基于运动非线性机制，建立大幅振动条件下垂向和俯仰耦合的精确非线性动力学模型，基于该模型可精确研究非线性车辆系统的复杂振动响应.

1 力学模型

1.1 动力学模型

如图1所示，行驶车辆系统模拟在不平道路上行驶车辆的振动力学简图.关于力学模型中参数设定如下：车辆的簧载质量为m，相对质心O的俯仰转动惯量为IC，前、后悬架弹簧支撑刚度分别为k1和k2，前、后悬架阻尼器的阻尼系数分别为c1和c2，车辆行驶速度为v，汽车质心横坐标和纵坐标分别为x和y，转动角为θ，质心O到前、后轴的距离分别为l1和l2，轴距为l=l1+l2，路面波长为l3，路面波幅h0.

图1 两自由度车辆模型Fig.1 The model of two degree-of-freedom vehicle

车辆前轮和后轮的垂向位移分别为y1和y2，假设路面波形状为：

式中，s=vt为行驶距离.

表 1 给出车辆系统参数的取值范围［10，11］，包括汽车簧载质量、汽车转动惯量、悬架刚度、悬架阻尼、轴距、速度、路面波幅和波长及几何尺寸等.

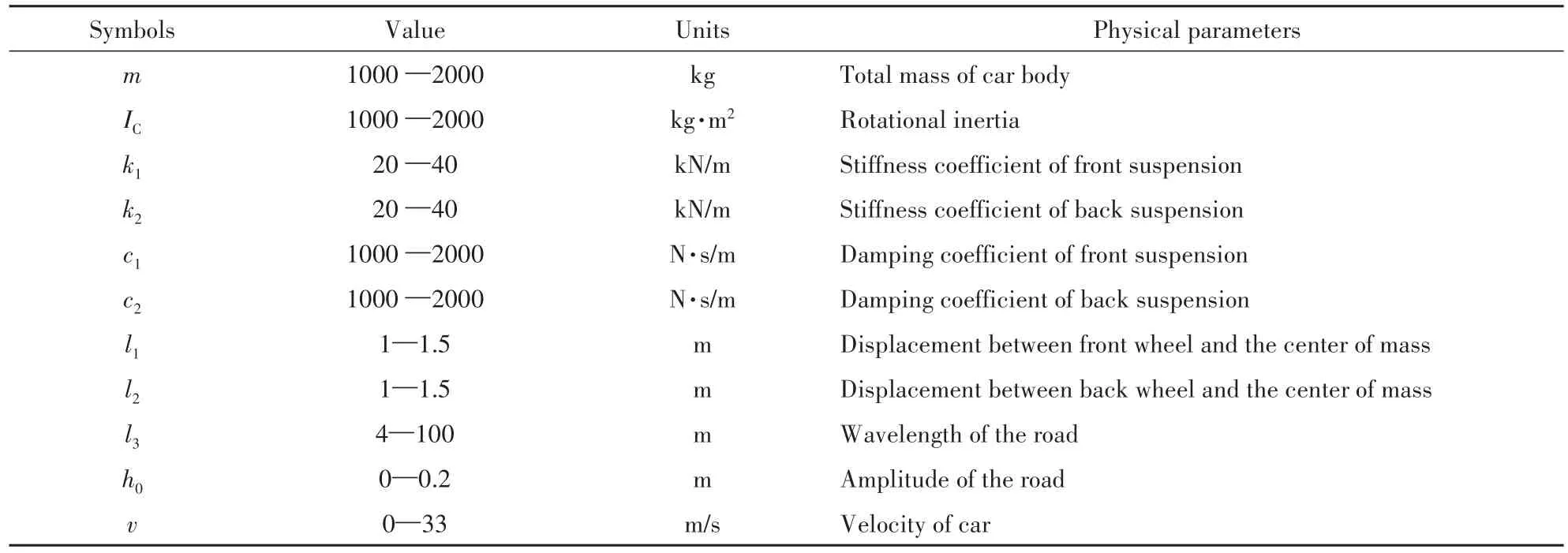
表1 汽车系统的参数列表Table 1 Parameters of vehicle system

设车辆系统的动能、势能及瑞利耗散函数分别为：

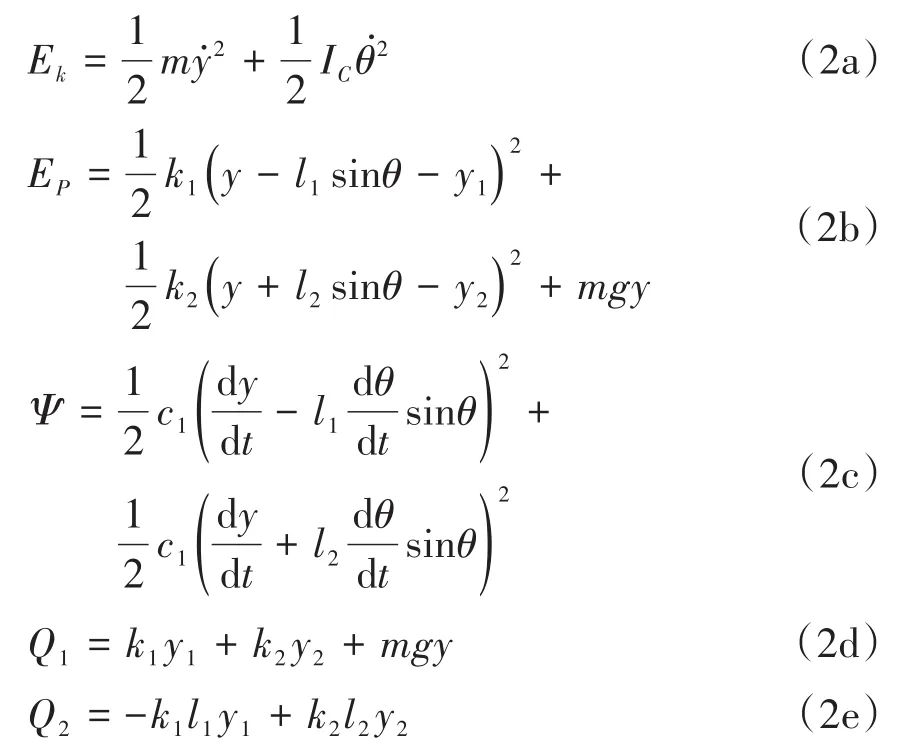
其中，ẏ=dy/dt，θ̇=dθ/dt分别为车辆质心的垂向速度和转动角速度；Q1和Q2广分别为垂向广义力和转向的广义力矩.

引入Lagrange函数：

既有保守力又有非保守力的Lagrange方程为：

将函数表达式（3）代入Lagrange方程（4）式，建立车辆行驶系统的两自由度非线性运动微分方程：

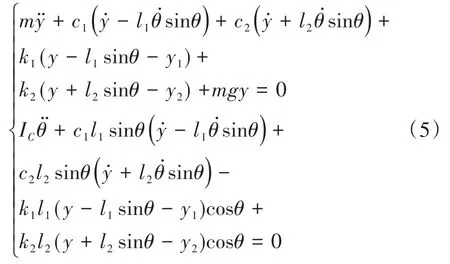
采用如下无量纲参数变换关系式：

将车辆振动系统（5）进行无量纲参数处理，得到非线性车辆系统的无量纲运动方程：

令Y′=U，θ′=ω，方程（7）可变换为如下一阶方程组的形式：

系统（8）是一个带有正弦和余弦三角函数的非线性振动耦合系统，具有复杂的非线性动力学响应行为.

1.2 非线性恢复力、势能及相图分析

系统（8）的无量纲非线性恢复力包括：垂直方向的恢复力fF和转动方向的恢复力矩fM.其分别为：

如图2所示，给出了非线性力函数（9）的曲面图，当参数β、γ和ρ的不同取值，图2（a，b）给出了回复力fF与俯仰角θ和垂向为Y之间为曲面关系，表明在两个振动方向上有较强的耦合回复力关系.图2（c，d）给出了力矩fM与俯仰角θ和垂向为Y之间也是曲面关系，但是在两个振动方向上的耦合力矩较弱.

图2 非线性力曲面图.（a，b）垂向恢复力，（c，d）转动力矩Fig.2Nonlinear forces.（a，b）vertical force，（c，d）rotational torque

系统（8）的无量纲势能函数为：

图3给出了无量纲势能函数（11）的曲面图.图3（a）为不考虑重力的势能曲面特性图，图3（b）给出了有重力情况下的势能曲面.

图3 势能曲线图Fig.3 Potential energy swryaces

积分车辆系统运动方程（8），可得到自由振动系统相轨迹方程为：

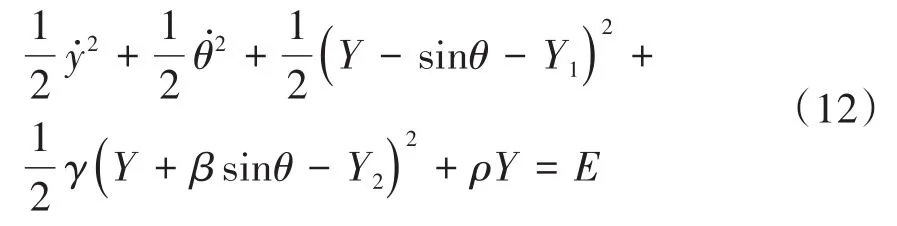
其中积分常数E为系统的总机械能，不同的机械能E对应于不同的相轨迹超曲面.

1.3 平衡点稳定性

令速度、加速度、角速度与角加速度均为零，定义平衡点集为：

对应的本征值方程为：

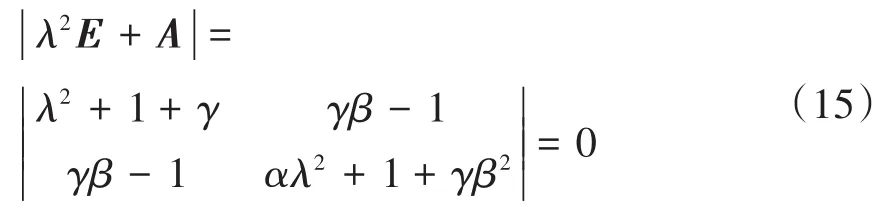
展开上式，得到：

令其系数分别为：

根据稳定性条件和Routh-Huritz判据，计算行列式：

利用式（18），可以分析系统参数对平衡点稳定性的影响规律.图4给出了参数平面（β，γ）中稳定区域与不稳定区域的分界曲线.当参数（β，γ）取值在曲线的上部为稳定区域，而在曲线的下部则为不稳定区域.

图4 参数（β，γ）平面中稳定区域图Fig.4 Stability diagram in parameters（β，γ）plane

2 自由振动

2.1 近似线性系统自由振动

针对非线性车辆系统（8）的自由振动，只保留y，θ及其导数得一次项，化简得到自由振动系统的线性运动微分方程为：

或者写为矩阵形式：

其中a=1+γ，b=c=1-γβ，d=1+γβ2.

令系统（20）的解为：

将式（21）代入方程（20），得到特征行列式：

式（22）给出了振动频率与系统参数之间的确定性关系，是关于ω2的二次代数方程，称为系统的特征方程，可以解出两个根为：

一阶固有频率ω1和二阶固有频率ω2由a、b、c、d确定，其中a、b、c、d由系统参数β、γ唯一确定.

将ω1和ω2分别代入系统（22），得到振幅比为：

得到一阶和二阶振型分别为

图5（a）为振幅比随参数β的变换趋势图，容易看出，系数β等于1是一个模态转换点.图5（b）为振幅比随参数γ的变换趋势图，同样，系数γ等于1是一个模态转换点.图5（c）为振幅比r1与参数β，γ关系图，图5（d）为振幅比r2与参数β，γ关系图.

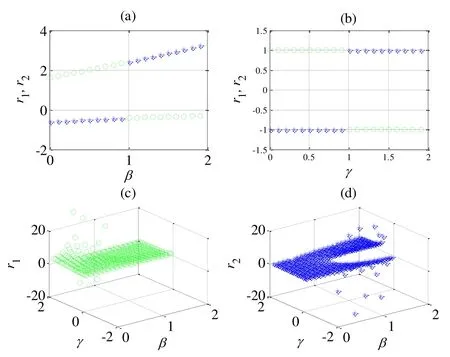
图5 振幅比与参数的关系.∘代表r1，*代表r2Fig.5 Relationship of ratio of amplitued and parameters.∘denoted r1，*denoted r2

2.2 非线性性近似系统的自由振动

针对车辆系统（8）的自由振动，如果保留x，θ及其导数得三次项，化简为非线性自由振动系统：

利用谐波平衡法，令系统（26）的一阶谐波解近似解为：

将解（27）代入非线性自由振动方程（26），得到振幅A1，A2与自由振动频率之间的关系，即幅频方程为：

将式（29）代入方程（28），得到：

给定φ的值，可以得到振动频率ω、振幅A1和A2，导出如下：

设定系统参数为 α=1，β=0.5，γ=0.5，并且令φ在适当的取值范围，图6给出了系统的幅频响应曲线，结果显示，非线性汽车振动系统的固有频率ω和模态参数均随振幅的变化而变化，得到ω=0.75和ω=1.45两个固有频率.

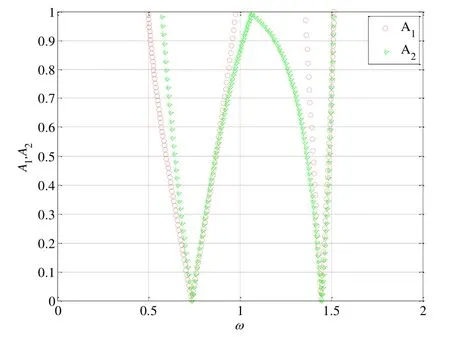
图6 振幅与自由振动频率的关系图Fig.6 Relationship of amplitude and frequency of free vibration

3 强迫振动

当考虑到路面对车辆的激励作用，导出强迫振动车辆系统的非线性动力学方程：

车辆系统（32）是一个复杂的非线性耦合动力学方程，无法直接用理论方法进行求解，本文利用数值积分的方法研究系统的振幅-速度响应特性图.

3.1 阻尼对响应的影响

设定汽车系统参数分别为m=1200kg，IC=1500kg·m2，k1=k2=20kN/m，l1=1.2m，l2=1.3m，l3=60m，h0=0.1m，容易得到无量纲参数为ω1=ω2=19.90 rad/s，α=0.868，β=1.08，γ=1.0，λ=41.667，ρ=0.049，ξ1=ξ2=0.0484，a=0.0833.

图7给出将阻尼分别设定为c1=c2=1000（红色圆圈○代表A1，红色加号+代表A2），c1=c2=1500（绿色三角形Δ代表A1，绿色星形*代表A2），c1=c2=2000（蓝色方形□代表A1，蓝色五角星★代表A2），得到速度振幅响应图.研究表明，振幅A1最大值分别为0.9，0.6和0.45，增大阻尼可以有效的减小振幅A1；而对振幅A2则减小效果较小，最大振幅分别为0.45，0.29和0.28.

图7 振幅与速度关系图Fig.7 Relationship of amplitude and velocity

3.2 路面波幅对响应的影响

设定参数分别为m=1200kg，IC=1500kg·m2，k1=k2=20kN/m，c1=c2=1500Ns/m，l1=1.2m，l2=1.3m，l3=50m，得无量纲参数为 ω1=ω2=19.90rad/s，α=0.868，β=1.08，γ=1.0，λ=41.667，ρ=0.049，ξ1=ξ2=0.0484.

图8给出波幅分别为h0=0.05（红色圆圈○代表A1，红色加号+代表A2），h0=0.1（绿色三角形Δ代表A1，绿色星形*代表A2），h0=0.15（蓝色方形□代表A1，蓝色五角星★代表A2）的速度振幅响应图，结果显示：增大路面波幅h0将导致振幅A1增大，最大振幅分别为0.3，0.6和0.9；同样导致振幅A2的，增大振幅分别为0.18，0.29和0.38.

图8 振幅与速度关系图Fig.8 Relationship of amplitude and velocity

3.3 路面波长对响应的影响

设参数分别为m=1200kg，IC=1500kg·m2，k1=k2=20kN/m，c1=c2=1500Ns/m，l1=1.2m，l2=1.3m，h0=0.1m，则有无量纲参数为ω1=ω2=12.90 rad/s，α=0.868，β=1.08，γ=1.0，λ=83.333，ρ=0.049，ξ1=ξ2=0.0484，a=0.0833.

图9给出不同路面波长时，即l3=30（红色圆圈○代表A1，红色加号+代表A2），l3=60（绿色三角形Δ代表A1，绿色星形*代表A2），l3=90（蓝色方形□代表A1，蓝色五角星★代表A2），分别得到速度振幅响应图.容易发现，增大路面波长对振幅A1减和振幅A2的影响，振幅A1共振速度分别为V=6，11及17，振幅A2共振速度分别为V=5，10及15，结果表明，路面波长越大共振速度越大，这与工程实际是相符的.

图9 振幅与速度的关系图Fig.9 Relationship of amplitude and velocity

4 小结

针对行驶中的车辆系统，建立了新型两自由度非线性耦合振动车辆系统，通过理论分析与数值研究得到如下结论：

（1）在运动非线性机制基础上，建立了上下沉浮和前后俯仰的车辆力学模型，利用Lagrange方程推导出系统的精确运动微分方程，带有三角函数的非线性方程可以精确地刻画车辆系统的非线性特性.

（2）对于线性系统的自由振动，分析得到振幅比随系统参数的变换曲线，发现振幅比在1处有一个转换点；对于非线性近似系统的自由振动，利用谐波平衡法得到幅频响应曲线，发现在0.75和1.45处两个固有频率.

（3）针对车辆系统的非线性动力学系统，利用数值仿真分析系统的振幅-速度响应关系图，研究结果表明：阻尼越大振幅响应越小、路面波幅越大响应振幅越大及系路面波长越大共振速度越大.