中国医药供应链分析——基于博弈论视角的药品定价模型

吴苏寒

引言

在2000 年，中国就已经拥有了298408 家医疗机构，其中包括19852 家公立医院[1]。这些公立医院面临的环境往往并不单纯，诸如政策，道德约束和利润追求等各种因素都有可能影响它们的运作。正如 Sun, Santoro, Meng, Liu 和Eggleston 提到的那样，对有些医院来说，药品销售有时甚至涵盖该医院超过一半的收入[2]。本文将根据现有的药品供应链结构，构建零售药店和医院药品定价竞争的博弈模型，尽管我们在这里提供的仅仅是一个确定性模型，但我们仍然期望它可以对现存现象给出一些解释。

在过去的几十年中，尽管中国医药产业不断发展，但迅猛的经济扩张同时也带来不少问题。销售假药、药品短缺及抗生素滥用等问题不仅侵害了医药产业，也会侵蚀中国国民健康保障系统。

根据网络资料显示，2019 年7 月，山东省公共资源交易中心发布《关于阿糖胞苷等短缺药品直接挂网公示的通知》，直接将阿糖胞苷等短缺药品挂网公示。公示的数种药品中，包括用于治疗恶性血液疾病的阿糖胞苷，以及青霉素替代药品——乳糖酸红霉素等医保甲类药品[3]。造成药品短缺的原因显然并不单一，但我们认为，或许可以从医院和药店的竞争关系中，找到些许原因，这也正是本文试图构建医院——药店博弈模型的动机。

本文对中国医药供应链结构的总结主要来源于Yu, Li 和Shi 在2010 年的工作[1]。他们描述了医疗改革前后的药品供应链状况，并对中国当时的医疗保障改革给出了一些评论。根据他们的介绍，我们分别绘制了中国传统医药供应链（见图1-1）和医疗改革之后医药供应链（见图1-2）的拓扑结构图。

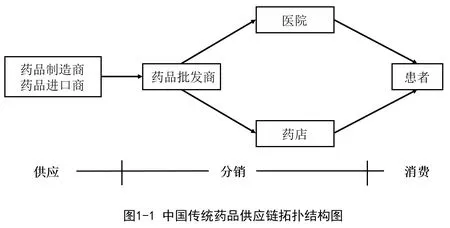
比较图1-1 和图1-2，我们会发现，相较于传统的医药供应链，改革之后的供应链丰富了药品分销渠道，它使得药品供应商不仅能将产品销售给批发商，也可以直接销售给医院和药店等零售商。因此，在图1-2 所示的供应链中，我们可以认为药店和医院有着平等的竞争关系，它们会在一定的限制条件下，通过调整药品售价，追求利润的最大化。

虽然已经有许多学者研究过报童模型，但是，我们经查阅发现，将报童模型的相关讨论延伸至药品供应链领域的工作还未出现。Bernstein 和Federgruen[4]把博弈论应用到了报童模型中，他们建立了包含N 个零售商的随机需求模型，研究了一个分散化的供应链，并指出，在这样的供应链中，通过合理的合同，分散化的供应链可以达到和集中化供应链相同的效率。在一般博弈模型中，Chen, Yan 和Li[5]证明了纳什均衡的存在唯一性，并指出，与合作博弈不同，竞争会使得纳什均衡点的售价更低。

本文基于Chen[5]的工作，将建立一个拥有竞价机制的报童模型，通过分析该模型的相关假设，论证模型的合理性，为未来的研究奠定基础。

1 医院——药店药品竞价模型概述

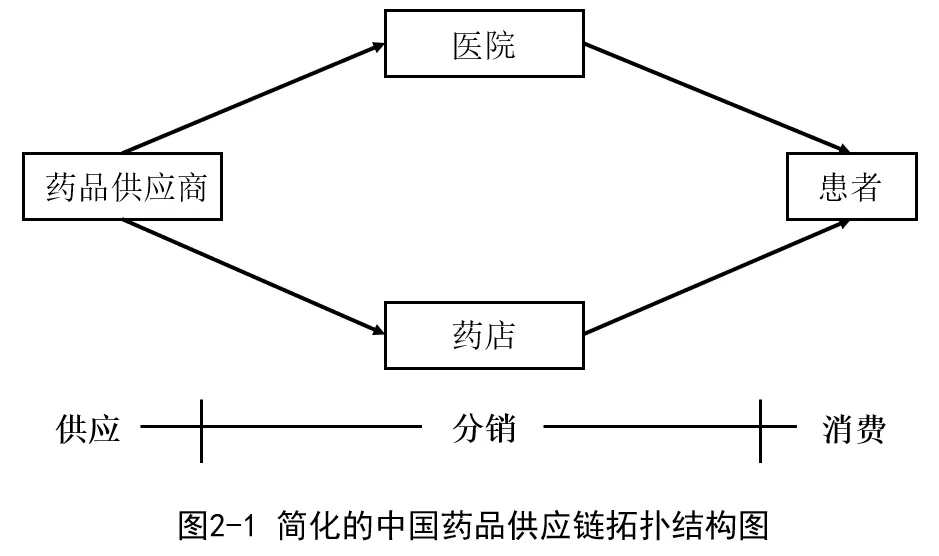
本节将概述模型的基本情况。从图1-2 可以看出，对于药品制造或进口商来说，有两种可能的分销途径，一种是先销售给药品批发商，再由批发商销售给医院和药店等零售商；第二种是直接销售给医院和药店等零售商。不论哪一种情况，消费者最终都会从医院或药店购买他们所需要的药品。

因此，不失一般性，我们可以将药品制造商或进口商与药品批发商合而为一，统称为药品供应商，图1-2 也就因此简化为图2-1 的形式。

我们将基本模型限制为只有一家医院和一家药店参与竞争，并由单一供应商供货的情况，并且他们各自只售卖一种针对慢性疾病的药品，尽管这与事实有较大的距离，但是可以作为我们研究问题的起点。

本文假设市场的药品需求是跟药品定价相关的随机变量，且供应商拥有无限的产能。对于医院和药店来说，他们的决策变量是药品订货量和定价，但对供应商来说，他的决策变量只有药品的出厂价格。

我们进一步假设患者只能有两种获得药品的途径，一是去医院看病并在医院开药；二是去药店直接买药。在基本模型中，我们将不讨论患者在医院获得处方，并去药店买药的情况。

在模型中，医院和药店的目标都是最大化各自的利润。整个模型的运行过程如下：首先，面对随机市场需求，医院和药店确定自己的订货批量和定价，最大化他们的利润。在观察到他们的订货批量和定价之后，药品供应商给出药品出厂价格，最大化自己的利润。换句话说，这是一个由药品供应商主导的市场，药品供应商在信息上占有优势。

该模型是一个静态非合作博弈模型，即每一个决策者只能决策一次。一般来说，有两种刻画随机需求函数的方法，一种被称为加法形式，即需求RD(p,ξ)=D(p)+ξ；[6]另一种被称为乘法形式，即需求RD(p,ξ)=D(p)•ξ。[7]不论哪一种形式，需求都被描述成一个确定性部分D(p)（价格p 的减函数）加（或乘）一个随机变量ξ 的形式。在我们的模型中，我们使用乘法形式来描述市场需求。

2 模型记号及假设

在本节中，我们将给出模型使用的记号和一些基本假设，并说明假设的合理性，现将本模型使用的记号罗列如下：

为了简便起见，在后面的叙述中，在不引起混淆的情况下，本文有时也使用Πd，Πh，Πs分别代替Πd(pd,ph,Qd)，Πh(pd,ph,Qh)和Πs(cd,ch).

下面，为了使本模型在不过分偏离真实情况的基础上，具有数学上的可讨论性，我们将给出九条假设，并逐一说明假设的合理性。

假设2.1 随机变量ξd和ξh独立于pd和ph，且E[ξd]=E[ξh]=1。 因此我们有E[RDd]=Dd(pd,ph,Ad), E[RDh]=Dh(pd,ph,Ah).

该假设说明，药品需求的总体趋势由售价决定，但其真实需求由一个服从某一分布的随机变量控制。

假设2.2 决策变量pd和ph只能分别在区间[cd,pd]和[ch,ph] 上变动，其中pd和ph分别为药店和医院该药品的最大零售价格。

我们称该假设是有意义的，因为显然医院和药店都不可能以低于进货成本的价格销售该药品，因此有pd≥cd，ph≥ch；同时，为了防止药品价格失控，政府往往会给出指导价格，将药品价格限制在一个合理范围内，因此，我们认为pd和ph均存在上限。

假设2.3 在[min(cd,ch),max(pd,ph)]上，Dd(pd,ph,Ad)对pd二阶连续可微； Dh(pd,ph,Ah)对ph二阶连续可微。且Dd(pd,ph,Ad)对Ad一阶连续可微，Dh(pd,ph,Ah)对Ah一阶连续可微。

假设2.4 说明，不论是对药店还是医院来说，他们自己的药品售价增长将导致自己的市场需求下降，并导致竞争对手的市场需求增加。假设2.5 则说明，医院比药店享有更高的声望值，正如Xuan Yu 所说，病人往往更加信任医院的诊断[1]。我们当然也很合理的假设，不论对于药店还是医院来说，市场需求都将随着他们的声望增加而增加。

假设2.7 ed和eh分别是ph和pd的单调非增函数，亦即∂ed/∂ph≤0，∂eh/∂pd≤0.

假设2.6 和假设2.7 告诉我们，药店（或医院）的药品售价增长不仅仅会降低自己的期望需求，也会降低其竞争对手的价格弹性。也就是说，当药店的药品定价不断升高时，它不仅变得更容易流失自己的顾客，也会让医院的顾客变得更加忠诚，反之亦然。

假设2.8 药店和医院均满足控制条件：∂ed/∂pd+∂ed/∂ph≥0，∂eh/∂ph+∂eh/∂pd≥0.

假设2.8 说明，不论对医院还是药店来说，自身价格改变的影响都要大于竞争对手价格改变的影响。我们认为这也是合理的，因为并不是所有顾客都会货比三家，他们应该会更多的受到自己常去购物的零售商的影响。

假设2.9 ξd和ξh分别均匀分布于[1-σd, 1+σd]和[1-σh,1+σh]上，其中σd,σh∈[0,1].

假设2.9 实际上是说药店和医院的市场需求将分别服从[(1-σd)Dd,(1+σd)Dd]和[(1-σh)Dh,(1+σh)Dh]上的均匀分布。值得一提的是，若σd=σh=1，药店和医院的需求将均匀分布于[0,2Dd]和[0,2Dh]，这可以用来讨论有时没有任何患者需要药品的情况。

3 药店和医院的最优订货批量及定价策略

正如我们在模型概述中所言，药店和医院会先行根据市场需求，决定自己的药品最优订货量和售价。随后，药品供应商在观察到他们的决策后，会决定自己的药品出厂价格以最大化自己的利润。据此，我们可以写出他们的期望收益函数。

药店期望收益函数：

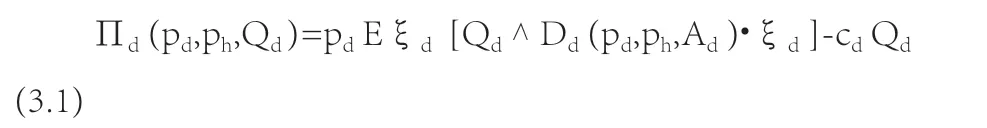
医院期望收益函数：

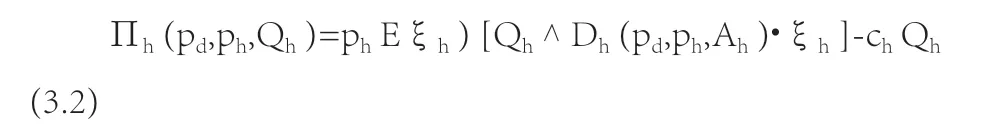
药品供应商期望收益函数：

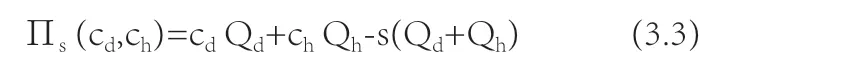
对给定的医院药品售价ph来说，药店面临的就是一个一般的报童定价问题。我们可以把药店的期望收益函数改写为

注意到Dd与Qd无关，因此我们可以求药店利润函数对订货量的偏导

下面，我们证明Πd和Πh分别是关于pd和ph的上凸函数。

定理3.1 在其它变量不变的情况下，药店和医院的期望收益函数Πd(pd,ph,Qd)和Πh(pd,ph,Qh)，分别是它们各自售价pd和ph的上凸函数。

证明：因为药店和医院的利润函数是对称的，因此我们只需要证明药店的情况即可。

于是，我们有 ,也就是说，Πd(pd,ph,Qd)是pd的上凸函数。

注意到医院和药店的对称性，我们可以类似得出，Πh(pd,ph,Qd)是ph的上凸函数。

定理3.1 和Πd对Qd的上凸性表明，在这个博弈模型中，（3.4）将始终成立。假若不然，药店的经营者总能在既定医院药品定价的前提下，修改订货批量以追求更大利润。因此，在给定医院药品定价ph时，药店所能做的唯一决策即是制定最优的pd以追求最大利润。这个陈述同样适用于医院的决策情况。

我们用 和 分别表示药店和医院的最优响应函数（best response function），下面，我们将证明，在本模型中，药店和医院的最有响应函数存在且具有唯一的解析表达式。

定理3.2 在我们的假设下，药店（或医院）的最优响应函数存在，并且具有唯一的解析表达式，

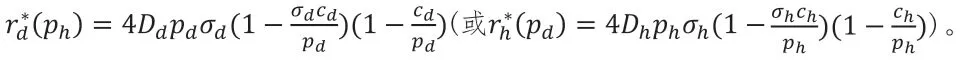
证明：考虑到医院和药店在模型中的对称性，我们在这里只需要讨论药店的情况即可。

根据定义[8]，为得到药店的最优响应函数，我们只需用Qd

＊替代（3.1）中的Qd即可。

将（3.4）带入（3.1）得

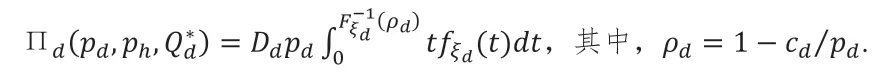
根据假设2.9，我们知道ξd服从[1-σd, 1+σd]上的均匀分布。

定理3.2 说明，基于我们第2 节中的假设，在简化的医药供应链中，可以建立合理的博弈模型，在市场运作工程中，药店和医院总是能够寻找到最优的订货批量，并根据竞争对手的定价，做出决策，我们可以期望，在未来的研究中能够从数学上证明这个博弈存在均衡点，并以此对现在市场上的一些现象给出解释。

4 结论

本文通过对现行中国医药供应链的分析，归纳了由医药供应商到患者的供应链结构图，建立了由医药供应商主导，药店和医院进行价格竞争的博弈模型。本文说明了模型假设的合理性，并基于模型假设，证明了药店和医院期望收益函数的凹凸性，并说明，不论对于医院还是药店来说，他们的最优订货批量始终存在，且与最优订货批量相关的最优响应函数能被唯一解析表出。这使得使用博弈论工具分析药店和医院的竞争成为可能。但是，本文尚未能论及医院和药店的竞争中，博弈均衡点是否存在唯一，而根据博弈均衡点的定价，解释医院和药店的竞争结果，并论述市场上许多廉价药品缺货现象的原因，可能会成为未来研究的一个方向。