基于双边界层滑模观测器的双轴直驱平台迭代学习轮廓控制

原浩， 赵希梅， 杜畅

(1.沈阳工业大学 电气工程学院，沈阳 110870；2.大连理工大学 控制科学与工程学院，辽宁 大连 116024)

0 引 言

目前，随着制造业对加工品质的需求日趋提高，由永磁直线同步电动机(permanent magnet linear synchronous motor, PMLSM)组成的双轴直驱平台因其响应速度快、定位精度高、可靠性好等特点已经广泛用于精密制造领域[1-2]。由于双轴之间运动不协调和系统存在的参数变化、摩擦力等不确定性，从而产生的轮廓误差将严重影响伺服系统的轮廓控制性能[3-4]。因此必须保证双轴的协调控制并对系统的不确定性进行补偿，以减小轮廓误差。

为满足双轴直驱平台的轮廓加工要求，文献[5]通过交叉耦合控制(cross-coupled control, CCC)，将实际轮廓近似为直线轮廓，利用双轴的跟踪误差计算得到轮廓误差，达到减小轮廓误差的目的。但这种方法仅适用于斜率缓慢变化的线性轮廓，在加工高进给率和存在尖角的轮廓时，该方法产生的轮廓误差较大。为了克服这一问题，文献[6]在切向轮廓控制中提出了坐标变换的方法，将沿轮廓法线方向的跟踪误差分量近似为轮廓误差；在此基础上，文献[7]提出一种在全局任务坐标系下建立的轮廓误差模型，在高进给率的参考轮廓下能够有效地减小轮廓误差。然而该方法需要建立准确的轮廓误差模型，对于复杂轮廓难以适用[8]。文献[9]提出了一种基于牛顿极值搜索算法的动态轮廓误差估计来搜索轮廓误差点，对轮廓误差进行精确估计。但低通滤波器可能会导致相位滞后。文献[10]提出一种迭代学习控制器(iterative learning controller,ILC)，通过学习轮廓误差的估计量提高下一次迭代的轮廓精度。然而，ILC对系统的不确定性非常敏感，这导致了系统鲁棒性受到影响。因此对系统的不确定性进行补偿也十分关键。文献[11]提出一种模型预测控制器和扰动观测器相结合的控制方法，利用扰动观测器对系统的不确定性进行观测，提高系统的鲁棒性。文献[12]提出了一种滑模观测器(sliding mode observer, SMO)用于补偿含有非线性不确定性的系统，然而滑模观测器的抖振问题并未解决。

因此，本文采用自适应迭代学习控制器(adaptive iterative learning controller, AILC)和SMO相结合的控制方法。在任务坐标系下建立轮廓误差模型，利用AILC对轮廓误差进行控制，对于高进给率和存在尖角的轮廓进行有效跟踪；采用双边界层SMO对扰动进行补偿，通过改变的双边界层厚度有效地削弱抖振，从而提高系统的鲁棒性。最终，实验结果验证了所提出的控制方案能够减小系统轮廓误差，满足双轴直驱平台高精密加工要求。

1 双轴直驱平台伺服系统数学模型与轮廓误差分析

1.1 双轴直驱平台伺服系统数学模型

双轴直驱平台伺服系统的电磁推力方程和机械运动方程为

Fei=Kfiiqi，

(1)

(2)

式中：Fei为电磁推力；Kfi为电磁推力常数；iqi为q轴电流；vi为动子速度；Mi为动子总质量；Bi为粘滞摩擦系数；Fi为包括系统参数变化、摩擦力等非线性不确定性的扰动；i=1或2。

假设不存在扰动Fi，根据式(1)和式(2)得到理想状态下的动态方程为

(3)

式中：di为动子位置；Ani=-Bi/Mi，Bni=Kfi/Mi，ui=iqi为控制器输出。考虑各种不确定性因素存在时，则式(3)变为

(Cni+ΔCi)Fi=

(4)

式中：Cni=-1/Mi；ΔAi、ΔBi和ΔCi为系统参数Mi和Bi所引起的不确定量；Hi为系统不确定性总和，表示为

(5)

假设Hi有界，即|Hi|≤ρi，ρi为正常数。

1.2 轮廓误差分析

在任务坐标系中，双轴直驱平台伺服系统产生的轮廓误差示意图如图1所示。

图1 轮廓误差示意图Fig.1 Schematic of contouring error

在Σw坐标系中，双轴直驱平台伺服系统的实际位置为

(6)

式中，t为时间。参考轮廓为

(7)

定义跟踪误差为期望位置点到实际位置点的距离，表示为

(8)

在Σl坐标系中，跟踪误差表示为

(9)

式中：en为法向分量；et为切向分量；θ为倾斜角。

轮廓误差为实际位置到参考轮廓的垂直距离，用跟踪误差的法向分量en近似表示。在Σw坐标系中对en进行正交分解

en=[en1en2]T=Rnew，

(10)

2 基于AILC和SMO的双轴直驱平台伺服系统系统设计

基于AILC和SMO的双轴直驱平台伺服系统框图如图2所示。其中，Cpx1，Cpx2为位置环控制器；Cvx1，Cvx2为速度环控制器，这4个控制器均设计为PI控制器。

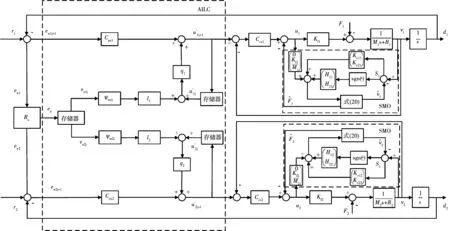
图2 基于AILC和SMO的双轴直驱平台伺服系统框图Fig.2 Block diagram of dual axis direct drive platform servo system based on AILC and SMO

2.1 AILC设计

ILC可以在没有精确的动态模型的情况下自动生成最佳控制信号，因此广泛地应用于高精密运动控制系统中[13-14]。ILC输入—输出关系为

(11)

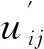
kewj+1(t)。

(12)

q(b-1)ψPjkPLenj(t)+

q(b-1)ψDjkDL{enj(t)-enj(t-1)}，

0≤t≤T-1。

(13)

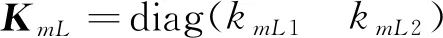
(14)

为验证系统的稳定性，将脉冲信号输入到系统的动态方程，形成提升系统。则式(11)的提升形式为

(15)

那么，式(12)的提升形式为

(16)

式中

(17)

式(17)代入式(16)，得

(18)

(19)

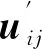
2.1 双边界层SMO设计

为了观测系统中的扰动，SMO设计为

(20)

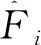
(21)

式中：β1为正常数，表示第一层边界的厚度；emax为误差的最大值；β2为第二层边界的厚度

(22)

当误差减小时，β2将扩大并降低SMO的观测范围；当误差由于不确定性的存在而增加时，β2将收缩以提高SMO的观测范围并使得误差控制在一定范围内。这种双边界层SMO增强了观测器的鲁棒性，并可以有效地削弱抖振。

为验证双边界层SMO的稳定性，选择Lyapunov函数为

(23)

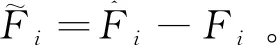
式(23)求导，得

(24)

式(20)代入式(24)，得

(25)

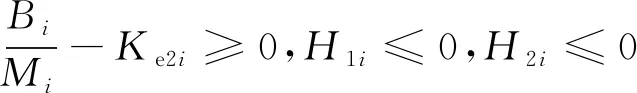
3 系统实验分析

实验中选择慧摩森科技公司生产的LM22-26系列XY平台作为控制对象进行实验研究。采用美国GSI公司的Micro-EMercury II 1600-40型光栅编码器作为两轴位置传感器，X-RS232与Y-RS232分别为PC与X轴、Y轴的驱动器通讯口。XY平台伺服系统硬件结构图如图3所示。

图3 XY平台伺服系统的硬件结构图Fig.3 Hardware structure diagram of XY table servo system

为验证双轴直驱平台伺服系统的跟踪性和鲁棒性，对系统输入r1=0.02cos(πt)，r2=0.02sin(πt)的圆形轮廓，并在2 s对两轴同时施加50 N负载，系统产生的轮廓误差如图4所示。从图4(a)、图4(b)可以看出，采用AILC产生的轮廓误差的均方根值为0.75 μm；采用AILC-SMO产生的轮廓误差的均方根值为0.4 μm。这表明两种控制方法都可以较好得跟踪轮廓。系统突加负载时，AILC产生的轮廓误差为8.8 μm，而AILC-SMO产生的轮廓误差为4.64 μm。因此，AILC对系统的不确定性比较敏感，鲁棒性受到影响；而AILC-SMO能够有效地跟踪系统轮廓，同时可以对系统的不确定性进行补偿，具有较好的鲁棒性。

图4 圆形参考轮廓实验结果Fig.4 Experimental results of circular reference contour

为了进一步验证AILC-SMO的性能，对系统输入r1=0.06cos(πt)，r1=0.02sin(πt)的高进给率椭圆形轮廓，系统产生的轮廓误差如图5所示。在初始时刻AILC产生的轮廓误差最大值为9.2 μm，轮廓误差的均方根值为1.04 μm；AILC-SMO产生的轮廓误差最大值为5.87 μm，轮廓误差的均方根值为0.52 μm。因此，AILC-SMO对于高进给率的轮廓可以产生优异的轮廓加工性能。

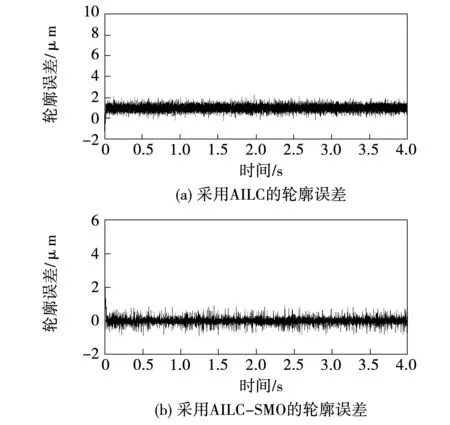
图5 椭圆形参考轮廓实验结果Fig.5 Experimental results of ellipse reference contour

当系统输入如图6(a)所示的r1=0.01cos3(πt)，r2=0.01sin3(πt)的星型参考轮廓时，双轴直驱平台伺服系统的轮廓误差曲线如图6(b)所示。

图6 星形参考轮廓实验结果Fig.6 Experimental results of astroid reference contour

比较两组曲线发现，AILC在尖角处产生的最大轮廓误差约为7.4 μm，AILC-SMO在尖角处产生的最大轮廓误差约为4.5 μm。AILC在曲线的平滑处可以产生良好的跟踪轮廓，但是在尖角处的轮廓跟踪性能恶化；而AILC-SMO可以更精确地跟踪尖角处的参考轮廓，因此该控制方案有效可行。

4 结 论

针对双轴直驱平台伺服系统的高精密轮廓控制问题，考虑到复杂轮廓以及不确定性因素使得伺服系统的轮廓性能恶化，提出了AILC和SMO相结合的鲁棒迭代学习轮廓控制方案。在全局任务坐标系下将跟踪误差的法向分量估计为轮廓误差，采用AILC对轮廓误差进行控制；利用双边界层SMO对系统的扰动进行观测和补偿，增强了观测器的鲁棒性。从理论上分析了AILC的稳定性与收敛性和SMO的稳定性。实验结果表明，采用的控制方案有效可行，减小了系统的轮廓误差，具有较强的鲁棒性，实现了高精密轮廓控制。