逆变器驱动式六极径向-轴向混合磁轴承结构原理及性能分析

朱熀秋， 周睿

(江苏大学 电气信息工程学院，江苏 镇江 212013)

0 引 言

随着现代工业对转子转速的要求不断提高，传统的滚动轴承和滑动轴承越来越难以满足其发展需求[1]。磁悬浮轴承(简称磁轴承)是一种利用麦克斯韦力使转子稳定悬浮于平衡位置的支承装置，实现了转子与轴承之间无机械接触，因而具有无摩擦、无磨损、无需润滑、无污染、高速度、高精度以及可在超净环境下工作等一系列传统轴承无可比拟的优点，在生命科学、能源交通、工业制造、航空航天等领域有广阔的应用前景[2-4]。

目前研究最为广泛的磁轴承是四极和八极结构，此类结构至少需要4个单极性(或2个双极性)直流功率放大器驱动。由于直流功率放大器体积大、成本高，限制了该类磁轴承的推广和普及[5-6]。若减少磁轴承的磁极个数，就能减少所需的直流功率放大器的个数，进而降低磁悬浮轴承系统的整体成本[7]。而要产生两个方向上的可控悬浮力，至少需要3个磁极，因此有学者提出了三极磁轴承[8]。相比于使用直流功放驱动，三相逆变器驱动技术更加成熟且价格便宜，更适合驱动三极磁轴承。文献[9]提出了一种采用三相逆变器驱动的三极主动磁轴承，证明了逆变器驱动的可行性。文献[10]设计了三极径向-轴向混合磁轴承，径向控制线圈由逆变器驱动，永磁体提供径向和轴向的偏置磁通。这种结构减少了转子的轴向长度，有利于临界速度的提高。文献[11]针对逆变器驱动式三极磁轴承非线性、强耦合的特点，采用神经网络逆实现了解耦控制。文献[12]分析了逆变器驱动对磁轴承承载力的影响，由于必须满足三相电流之和为零的条件以及三极的空间不对称性，x轴方向的最大悬浮力与y轴方向的最大悬浮力存在差异。文献[13]研究了逆变器驱动式六极磁轴承，其3个磁极缠绕控制线圈，3个磁极嵌有永磁体。在稳态运行时，功率损耗只有八极磁轴承的13.35%。

虽然，逆变器驱动式三极磁轴承拥有诸多优点，然而必须采用有效的非线性解耦控制方法才能实现磁轴承的高性能运行，这也增加了系统的整体设计难度与成本[14-16]。本文针对三极结构非线性和强耦合的特点，提出了一种六极径向-轴向混合磁轴承。首先，介绍了逆变器驱动式六极径向-轴向混合磁轴承的结构与工作原理，并推导出其非线性数学模型。然后，通过三维有限元仿真得出三极结构与六极结构的力-电流特性和最大承载力，并将结果与理论值进行对比分析。最后，通过实验验证了六极结构的优越性。

1 逆变器驱动式六极径向-轴向混合磁轴承数学模型

1.1 逆变器驱动式六极径向-轴向混合磁轴承结构及工作原理

逆变器驱动式六极径向-轴向混合磁轴承主要由永磁体、径向定子、轴向定子、转子、轴向线圈和径向线圈组成。其中，永磁体沿径向充磁。径向定子由圆环形径向定子轭和沿圆周均匀分布的6个磁极组成。轴向定子由1个圆环形轴向定子筒和2个带轴向磁极的轴向定子圆盘构成。转子置于轴向磁极和径向磁极中间，分别留有轴向气隙和径向气隙。6个径向控制线圈分别缠绕在6个径向磁极上，相对的2个线圈串联且缠绕方向相同，作为一相，三相线圈采用星型链接。轴向控制线圈安装于轴向定子内侧，控制磁通由控制线圈产生，偏置磁通由永磁体产生。

当磁通流经磁极和转子之间的气隙时，就会在转子表面产生相应的麦克斯韦力。控制磁通的方向和大小就可以控制麦克斯韦力的方向和大小，最终使转子悬浮在平衡位置，如图1所示。

图1 六极径向-轴向混合磁轴承结构与磁路Fig.1 Structure and flux paths of six-pole radial-axial hybrid magnetic bearings

图1中：磁极A1和磁极A2统称为A相磁极，同理，磁极B1和磁极B2称为B相磁极，磁极C1和磁极C2称为C相磁极。由于每相磁极上径向控制线圈的缠绕方式相同，所以在径向气隙中产生的控制磁通方向也相同，而永磁体产生的偏置磁通在相对的径向气隙中方向相反，从而偏置磁通和控制磁通在径向气隙中叠加后，会使相对的2个径向气隙中的一个磁通增强，另一个气隙磁通削弱，最终产生可控径向悬浮力。通过改变径向控制电流的方向和大小，就可以得到可控径向悬浮力。在轴向气隙中，一侧气隙中控制磁通和偏置磁通互相增强，另一侧气隙中控制磁通和偏置磁通互相削弱，从而得到可控的轴向悬浮力。

1.2 逆变器驱动式六极径向-轴向混合磁轴承数学模型

根据等效磁路法对图1进行分析，忽略涡流效应、漏磁、软磁体磁阻等因素的影响，可以得到逆变器驱动式六极混合磁轴承的等效磁路图，如图2所示。

图2 六极径向-轴向混合磁轴承等效磁路图Fig.2 Equivalent magnetic circuit of six-pole radial-axial hybrid magnetic bearings

图中：Fm是永磁体的磁动势；Φm为总磁通；ΦZ1、ΦZ2分别为两个轴向气隙处的磁通；ΦA1、ΦA2、ΦB1、ΦB2、ΦC1、ΦC2分别为6个径向气隙处的磁通；GZ1、GZ2分别为2个轴向气隙处的磁导；GA1、GA2、GB1、GB2、GC1、GC2分别为6个径向气隙处的磁导；NZ为轴向控制线圈的总匝数；Nr为每相径向控制线圈的总匝数；iA、iB、iC分别为每相径向控制线圈中的径向控制电流；iZ为轴向控制电流。轴向和径向的气隙处磁导可表示为：

(1)

式中：μ0为真空中的磁导率；δr、δZ分别表示转子处于中心平衡位置时径向、轴向的气隙长度；Sr、SZ分别为径向磁极面积和轴向磁极面积；x、y为转子径向位移；z为转子轴向位移。

根据磁路基尔霍夫定律可以计算出每个气隙处的磁通为

(2)

式中：

GZS=GZ1+GZ2；GZM=GZ1-GZ2；Gr=GA1+GA2+GB1+GB2+GC1+GC2；Gsum=GZ1+GZ2+GA1+GA2+GB1+GB2+GC1+GC2；Фrc=∑Nrij(Gj1-Gj2)，j=A,B,C。

根据磁通和麦克斯韦力之间关系F=Ф2/μ0S，就能够得出每个气隙中产生的悬浮力表达式：

(3)

式中j=Z1,Z2,A1,A2,B1,B2,C1,C2。

将各个磁极产生的悬浮力在对应的坐标轴进行合成，所得到的轴向和径向悬浮力为：

(4)

2 三极结构与六极结构的对比分析

2.1 理论分析

六极结构与三极结构的基本结构相同，不同之处是径向定子具有6个径向磁极，在原有的3个磁极的对面再增加3个磁极，弥补了三极结构空间不对称的缺陷，如图3所示。

图3 三极与六极结构对比图Fig.3 Structure contrast of three-pole and six-pole

令转子处于中心位置，此时6个径向气隙的磁导相同(GA1=GA2=GB1=GB2=GC1=GC2=Gr0)，2个轴向气隙磁导的也相同(GZ1=GZ2=GZ0)，则可以将磁通的表达式进行简化，即

(5)

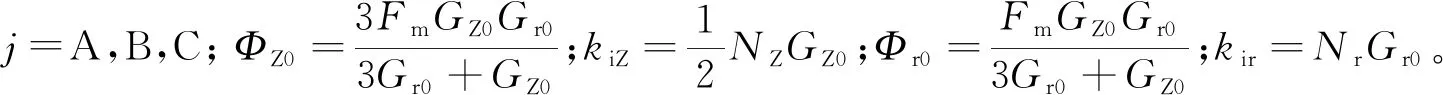
悬浮力表达式，将各个磁极产生的悬浮力投影至x轴和y轴且进行叠加，即

(6)

采用Clark变换，将三相电流(iA,iB,iC)转换为两相电流(ix,iy)代入上式可得

(7)

采用相同的方法进行分析，可以得出当转子处于平衡位置时，逆变器驱动式三极径向-轴向混合磁轴承的悬浮力表达式为

(8)

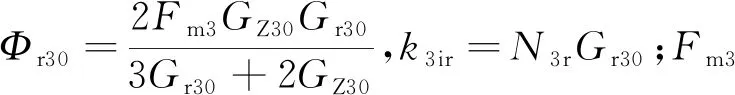
由式(8)可以看出，在逆变器驱动式三极磁轴承中，即使转子处于平衡位置，径向两个自由度之间依然存在耦合。在x轴方向，当iy保持不变，F3x与ix为二次非线性关系，当iy产生变化时，F3x与ix的关系曲线会随着的iy平方项向下平移；在y轴方向，当ix保持不变，F3y与iy为线性关系，当iy产生变化时，F3y与iy的关系曲线的斜率会随着ix的增加而减少。若转子发生偏移，那么径向悬浮力与控制电流之间的非线性会增强，且两自由度之间的耦合也会增强。可以得出结论：逆变器驱动式三极磁轴承是一个非线性、强耦合的系统。

由式(7)可以看出，在逆变器驱动式六极磁轴承中，当转子处于平衡位置时，x轴方向与y轴方向的悬浮力Fx、Fy与控制电流ix、iy呈线性关系且互相之间没有耦合。由此可以得出结论：六极结构在消除三极结构的空间不对称性后，从结构上提升了逆变器驱动式磁轴承的性能。

2.2 最大承载力对比分析

最大承载力是磁轴承的重要性能指标之一，分析六极结构的承载能力对磁轴承设计、控制和安装具有指导性的意义。为了使磁性材料工作在磁化曲线的线性区域，气隙中磁感应强度最大值选取软磁材料的饱和磁感应强度BS，当气隙中磁感应强度等于BS时，则该气隙下产生最大悬浮力。以x轴正方向的最大悬浮力为例，当A相磁极通入irmax时，磁极A1对应气隙的磁通达到饱和磁感应强度BS，磁极A2对应气隙的磁通为0，此时x轴正方向获得最大悬浮力，由于B相与C相电流需满足三相电流之和为零的条件，B相与C相通入-0.5irmax。根据式(5)可以分析x轴正方向的最大悬浮，即

(9)

由式(9)可得

(10)

此时B1、B2、C1、C2气隙中的磁通为：

(11)

将各个磁极产生的最大悬浮力在x轴方向进行合成，得到x轴方向最大悬浮力为

(12)

当B相通入正的最大电流irmax，C相通入负的最大电流-irmax时，y轴正方向获得最大悬浮力，采用与x轴相同的分析方法得到y轴的最大悬浮力

(13)

由表2可知，三极结构的每个径向磁极的面积为六极结构的两倍，计算最大悬浮力时统一采用六极结构的磁极面积Sr，参照文献[12]将三极结构和六极结构各个方向的最大悬浮力列表进行对比,如表1所示。

由表1可以得出，三极结构磁轴承的最大悬浮力在两坐标轴的4个方向上并不完全相同，x轴负方向悬浮力最小，y轴正负方向悬浮力大小一致，x轴正方向悬浮力最大。六极结构得益于其空间的对称性，x轴方向的悬浮力也是对称的，其y轴悬浮力与三极结构一致，其x轴悬浮力为y轴悬浮力的87%。三极结构x轴负方向的悬浮力为六极结构的75%。因此，在设计逆变器驱动式六极磁轴承时，其径向最大承载力要求只需满足x轴方向的最大悬浮力。相比于三极结构，提高了磁轴承的单位体积利用率。

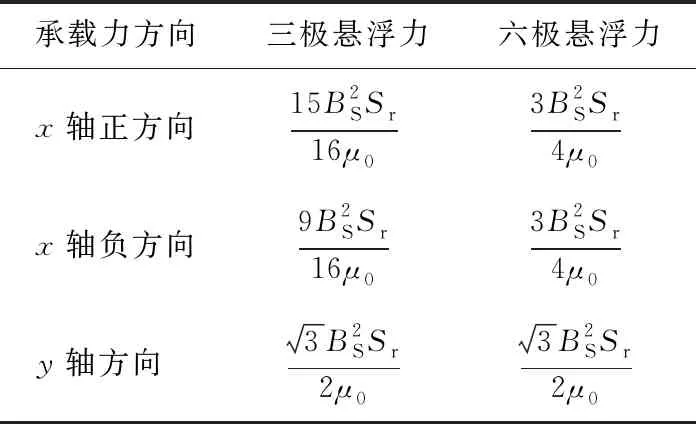
表1 各方向最大悬浮力

2.3 有限元仿真

为了更加直观地将三极结构与六极结构进行对比，验证理论分析的有效性，在ANSYS-Maxwell软件中建立了三维模型的网格剖分图[17]，如图4所示，为了方便观察，将轴向定子的部分隐藏。

图4 三维有限元网格划分图Fig.4 Mesh plot of 3-D finite element model

由于三极结构和六极结构在轴向结构上保持一致，为了保证两者参数具有一定的可比性，在保证总磁极面积与总线圈匝数相同的情况下，两种结构的具体参数如表2所示。

表2 六极混合磁轴承参数

为了验证式(7)与式(8)对六极与三极悬浮力-电流流特性的分析，在有限元软件中设置2个控制变量(ix、iy)，利用Clark反变换将A、B、C三相中对应的控制电流用ix、iy表示，保持转子悬浮在平衡位置，将电流源激励设置为-1.22 A～1.22 A，所得到力-电流特性曲线的仿真结果如图5所示。

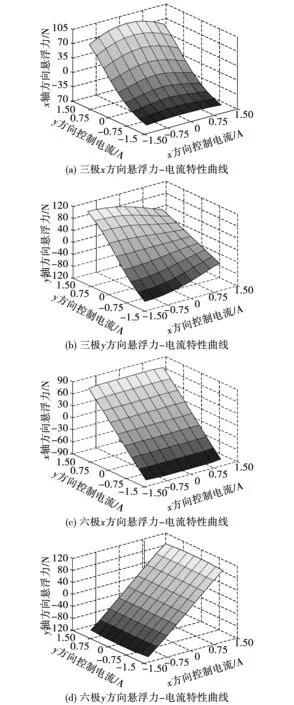
图5 悬浮力-电流特性曲线Fig.5 Curves of force-current characteristics

根据上述分析，在仿真三极结构时，当设置A相电流为320 At，B相与C相电流为-160 At，就可以得到x正方向的最大悬浮力。当设置A相电流为-320 At，B相与C相为160 At时，就可以得到x负方向的最大悬浮力。当设置B相电流为320 At，C相电流为-320 At时，就可以得到y方向的最大悬浮力。采用相同方法也可以仿真得到六极结构x方向与y方向的最大悬浮力。

由图5可以看出，由于三极磁轴承结构上的空间不对称性，导致了x轴方向的力-电流特性曲线不是中心对称的，虽然y轴的力-电流特性曲线是关于中心点对称的，但x、y轴的力-电流特性曲线的线性度都非常差；而六极结构得益于其空间结构上的对称性，使得x轴、y轴的力-电流特性曲线都关于中心点对称且具有良好的线性度，验证了理论分析的有效性。

3 实验论证

为了验证理论分析与有限元分析结果的有效性与正确性，在逆变器驱动式的磁轴承样机上进行验证实验。样机如图6所示。

图6 逆变器驱动式径向-轴向混合磁轴承样机Fig.6 Prototype of inverter-fed radial-axial hybrid magnetic bearing

3.1 非线性验证实验

按照以下几个步骤可近似的测量出悬浮力-电流特性曲线。首先，在A相通入1 A的电流，B相和C相均通入-0.5 A的电流，此时ix等效为1.22 A，转子在麦克斯韦力的作用下被吸至x轴正方向的辅助轴承处，此时的作用力由偏心磁拉力与可控悬浮力共同组成。使用弹簧测力计将转子往x轴负方向拖动，当转子被拖动时，记录下弹簧测力计的当前值。要测得控制电流产生的力需要再测得单边磁拉力的大小，所以将转子移动至x轴正方向的辅助轴承处且切除控制电流，使用弹簧测力计将转子往x轴负方向拖动，当转子被拖动时，弹簧测力计的读数即为偏心磁拉力的大小。将第一次的测量值与第二次的测量值相减，所得到的数值可近似地认为是控制电流所产生的悬浮力，这样就得到了一组悬浮力力电流关系的曲线。缓慢地减少iA的值且保证iB=iC=-0.5iA，即可测出x轴方向的悬浮力-电流特性曲线。同样的方法，保证iB=-iC，即可测出y轴方向的悬浮力-电流特性曲线。

图7中对比了计算值、有限元仿真值与实验值。图7(a)与图7(b)分别为六极结构x方向与y方向的悬浮力-电流特性曲线，其中仿真结果与实验结果以及式(7)理论分析结果基本吻合。图7(c)与图7(d)分别为三极结构x方向与y方向的悬浮力-电流特性曲线，其中仿真结果与实验结果以及式(8)理论分析结果基本吻合。可以得出结论：相比于三极结构，六极结构的悬浮力-电流特性曲线的线性度有了很大的提升。实验结果略大于理论值和仿真结果，是由于测量悬浮力是基于转子偏心的情况，而转子偏心会影响控制电流产生的悬浮力。

3.2 承载力验证试验

首先测量六极结构的最大悬浮力：在A相线圈中通入1 A的电流，B、C两相均通入-0.5 A的电流，此时转子被麦克斯韦力吸至x轴正方向，此时的作用力由偏心磁拉力与可控悬浮力组成。使用弹簧测力计将转子向x轴负方向移动，当转子被拖动时，测得作用力为127 N。断开所有的径向控制电流，推动转子使其吸附在x轴正方向上，使用弹簧测力计将转子向x轴负方向移动，当转子被拖动时测得作用力(偏心磁拉力)为36 N，则转子在x轴方向上的最大悬浮力可近似的认为是91 N。采用同样的方法可测得y轴方向的最大悬浮力以及三极结构各个方向的最大悬浮力。两种结构各个方向最大悬浮力的理论值，有限元仿真值与实验值分别如表3、表4所示。

表3 六极结构最大悬浮力

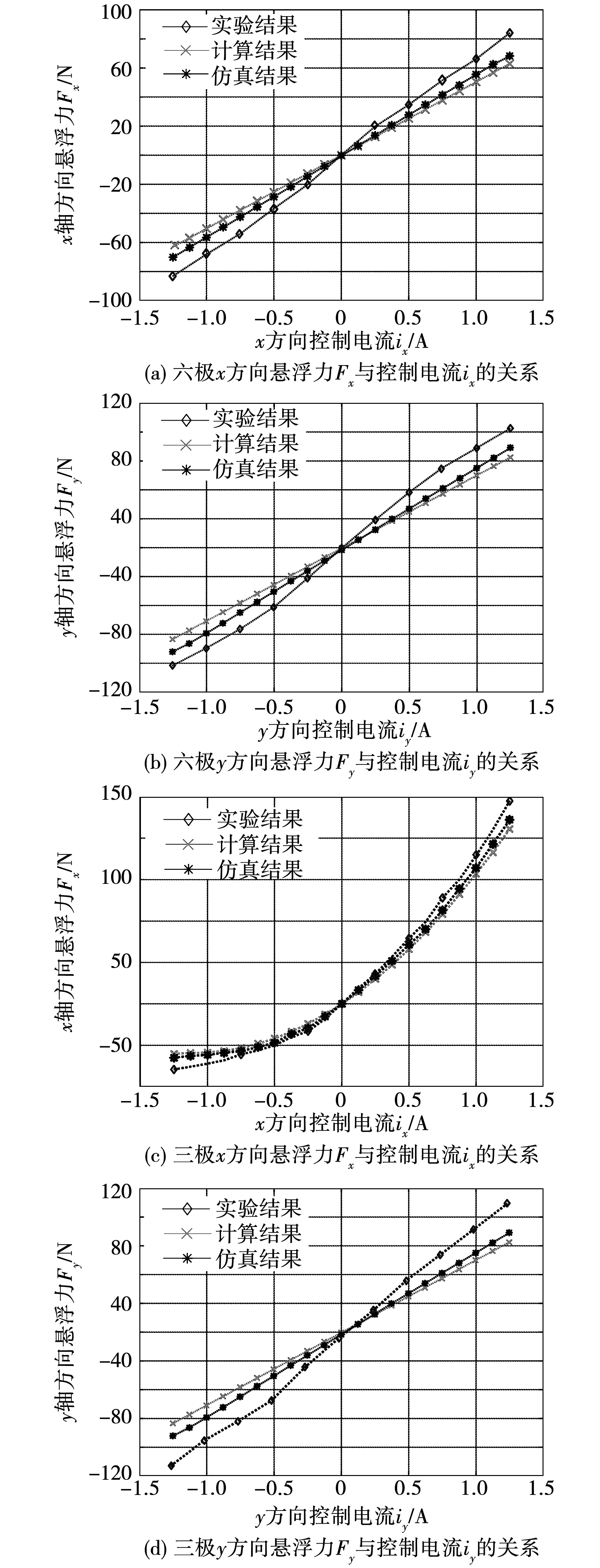
图7 径向悬浮力与控制电流的关系曲线Fig.7 Curves between suspension force and control current

采用同样的方法可以测量出三极结构的最大悬浮力，其各个方向最大悬浮力的理论值，有限元仿真值与实验值如表4所示。

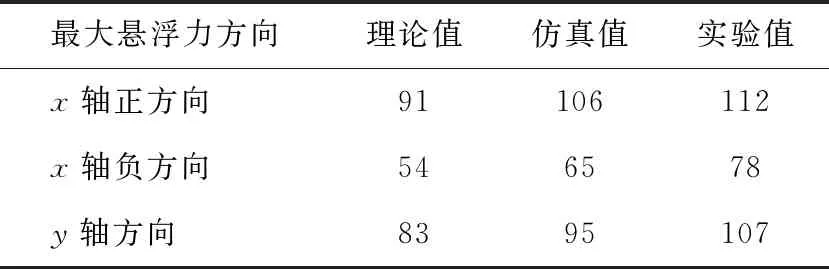
表4 三极结构最大悬浮力

对比表3与表4可以得出结论：在x轴方向，三极结构的正方向悬浮力最大，三极结构的负方向的悬浮力最小；在y轴方向，三极结构与六极结构的悬浮力基本一致。由于磁轴承的最大承载力取决于最大悬浮力中最小的一个，则三极结构的最大承载力为78 N，六极结构为91 N。所以，相比于三极结构，六极结构的最大承载力提高了16%，增加了磁轴承的单位体积利用率。

4 结 论

本文针对逆变器驱动式三极磁轴承非线性和强耦合的特点，提出了一种六极径向-轴向混合磁轴承。首先，采用等效磁路法建立了六极径向-轴向混合磁轴承的数学模型。然后，通过理论分析推导出六极结构与三极结构的力-电流特性表达式，并且通过三维有限元仿真将两者对比分析。最后，通过实验得出结论：得益于六极结构的空间对称性，其悬浮力-电流特性趋于线性，而三极结构有着很强的非线性。同时，六极结构的最大承载力相比于三极结构提高了16%，增加了磁轴承的单位体积利用率，验证了所提出的六极径向-轴向混合磁轴承的性能优势。