具有原边互感识别功能的恒流恒压无线充电系统开发
张文杰, 秦伟, 宋建成, 吝伶艳, 毕鲁飞
(1.太原理工大学 煤矿电气设备与智能控制山西省重点实验室,太原 030024;2.太原科技大学 电子信息工程学院,太原 030024)
0 引 言
无线充电系统主要由高频电压源、耦合线圈、地面和车载侧的补偿电路、车载整流器和充电电池组成[1]。地面侧和车载侧之间通过电磁场传递能量,避免了电缆的束缚,具有无需插拔、无需精确对准和无接触火花等优点,极大地提高了电动汽车充电的便利性和安全性,引起了国内外学者的广泛关注[2-3]。
无线充电系统中的补偿电路对实现恒流/恒压输出具有很重要的作用[4-6]。为了实现充电模式的切换,通常在原边和副边之间进行无线通信,将充电状态信号反馈到原边,采用变频控制或者开关切换原边补偿电路的方法[7-8]。但是,增加无线通信装置将增加系统的复杂性和不稳定性,特别是在磁场复杂的环境,并且由于原边电路在地面,增加了开关器件将可能提高运行维修成本。变频控制将容易引起分岔现象。此外,一些学者提出了通过切换副边补偿电路的方法来满足先恒流后恒压的充电需求,降低原边电路和控制的复杂度[9-13]。文献[11]提出了基于LCL谐振补偿网络的副边自动切换充电模式无线电能传输系统,减小了开关数量。但是,系统在恒压充电模式不能保持输入阻抗为纯阻性,降低了系统的传输效率。文献[13]提出了基于原边LCC补偿的副边切换拓扑,为实现恒流恒压输出,不仅需要多个开关,且没有考虑电感电流和电容电压特性,切换模式的安全性和稳定性较低。此外,一些补偿网络的恒流/恒压输出能力与漏感有关,耦合线圈的随机性偏移不仅会降低效率,还会影响系统实现恒流/恒压输出。所以,非常有必要设计一种可以省去通信、不受线圈参数约束、安全稳定运行、高效率的系补偿拓扑方案。
同时,由于两侧线圈之间没有物理连接,受司机驾驶技术和停车位客观条件的限制,线圈容易偏移是无线充电系统的重要特点之一。线圈的偏移将使两侧线圈的相对位置发生变化,相互交链的磁通减小,互感随之减小。但是,互感值对系统各处电流和电压的大小起着决定性的作用。所以,停车充电的位置发生偏移,两侧线圈偏离正对状态,充电电流和电压必将发生变化。针对这种工况,工程中通常采用增加前级调压电路来调节逆变器输入电压的方法或者移相调节逆变器输出电压的方法。同时,这也需要采用无线通信的方法将充电电池的状态信息传递到原边形成反馈控制环,从而使系统保持输出额定电流和电压。所以,提出根据互感与原、副边电气量之间的电路关系进行自动调节,省去无线通信环节,省去复杂控制策略的方法具有很大的研究意义和工程价值。
本文将在双LCC和LCC-S混合补偿拓扑的基础上,根据互感和逆变器输出电流的关系实现互感自动识别,从而直接移相调节逆变器输出的高频电压,开发一套允许偏移的电动汽车恒流恒压无线充电系统,仿真和实验结果验证混合补偿拓扑设计方案和基于原边互感自动识别的移相控制方法的可行性和有效性及系统具有良好的运行性能。
1 混合补偿拓扑原理分析
对于充电电池,为了避免出现过充或欠充的问题,通常采用先恒流后恒压的二阶段充电法,如图1所示,其中实线表示充电电流,虚线表示充电电压。在充电初期,对蓄电池输入恒定电流,端电压逐渐增加,充入大约60%的电量,具有较高的电能利用率。当端电压上升到恒压充电设定值时,切换到恒压充电模式,充电电流逐渐减小。在整个充电过程中,等效电阻RB不断增大。
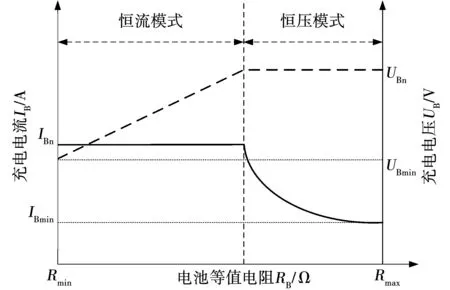
图1 二阶段充电模式图Fig.1 Two stage charging mode diagram
一次侧采用LCC补偿拓扑,一次侧线圈可实现恒流励磁,易于系统控制。并且,一次侧采用LCC补偿电路的无线充电系统不仅对谐振参数的准确度要求低,而且对电路寄生参数的敏感度低,充电电流/电压和互感基本为线性关系。针对线圈发生偏移进行移相控制的工况,线圈偏移量越大,充电电流/电压随电池等效电阻RB的变化率反而会越小。同时,采用LCC补偿拓扑,充电电流/电压可摆脱耦合线圈的约束,具有高的自由度。所以,本文基于一次侧采用LCC补偿拓扑的方式来设计副边自动切换的混合补偿拓扑,实现充电模式的切换。
1.1 双LCC补偿电路恒流输出工作原理
基于电流控制电压源(CCVS)的等效电路如图2所示,电压源输入经过V-C-1谐振网络变换为恒流源,一次侧线圈的电流I1为
(1)
所以,I1不受二次侧的影响,二次侧感应电压为恒压源。二次侧补偿网络结构和一次侧对称,电容Cs2不完全补偿L2组成等效电感Leq2,Leq2和电容Cs1构成V-C-2谐振网络,变换为恒流输出。
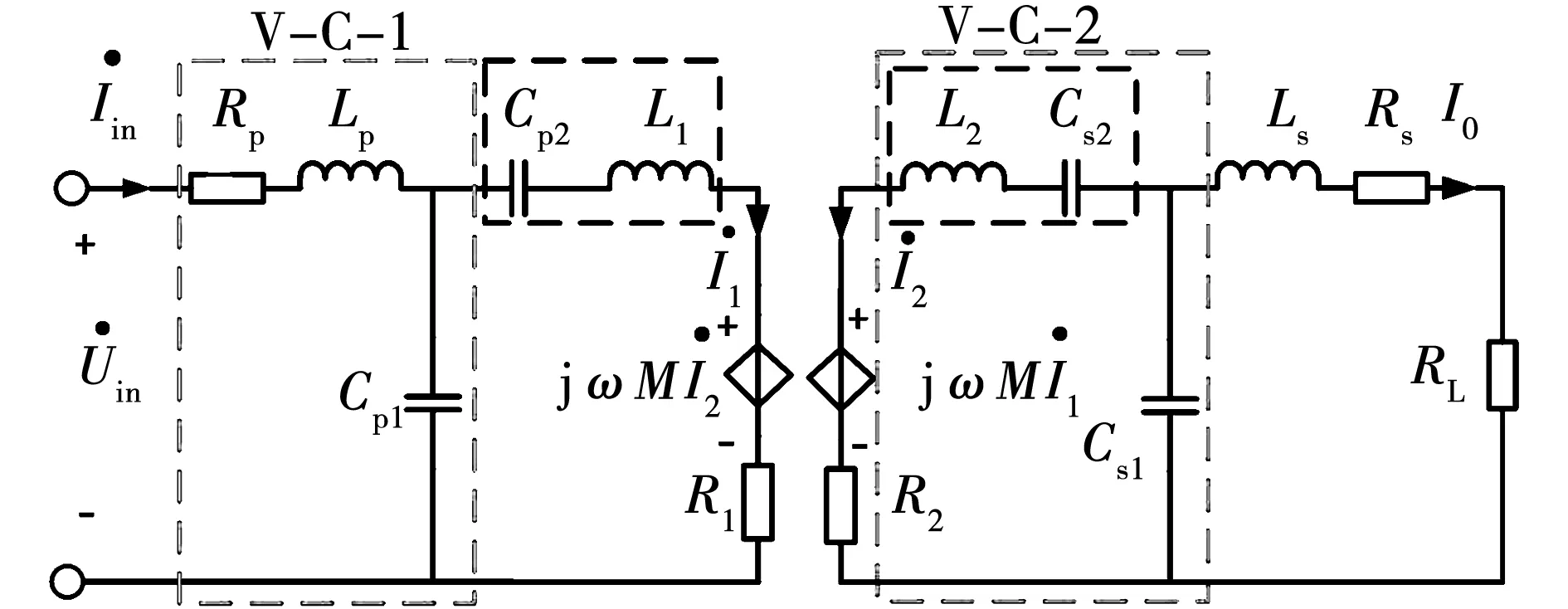
图2 双LCC补偿等效电路图Fig.2 Equivalent circuit diagram of double LCC compensation
同时,电容Cp2欠补偿一次侧线圈自感L1组成等效电感Leq1、Leq1和Lp相等,Leq2和Ls相等,分别和Cp1、Cs1组成反向LC谐振网络,输入阻抗将为纯阻性,不需要输入无功功率。
所以,双LCC补偿参数工作条件为
(2)
输出电流Io-双LCC为
(3)
在给定输入电压和耦合线圈的条件下,调整补偿电感Lp和Ls的值,即可得到所需的输出电流。
考虑耦合线圈电阻R1、R2和补偿电感以及开关器件寄生电阻Rp、Rs的存在,输出电流Io、输入电流Iin和效率η双LCC分别为:
(4)
(5)
(6)
式中:A=Rp{Rs[(ωM)2+R1R2]+R1(ωLs)2}+(ωLp)2(ωLs)2+R2Rs(ωLp)2+RL{R2(ωLp)2+Rp(ωM)2+R1R2Rp};B=Rs[(ωM)2+R1R2]+R1(ωLs)2+RL[(ωM)2+R1R2]。
1.2 LCC-S补偿电路恒压输出工作原理
等效电路如图3所示,一次侧电路和双LCC的一次侧相同。在二次侧回路,电容Cs2和线圈自感L2串联谐振,输出电压Uo等于二次线圈感应电压U2,与二次侧电路参数无关,实现了恒压输出,且实现了完全谐振,输入阻抗呈阻性。
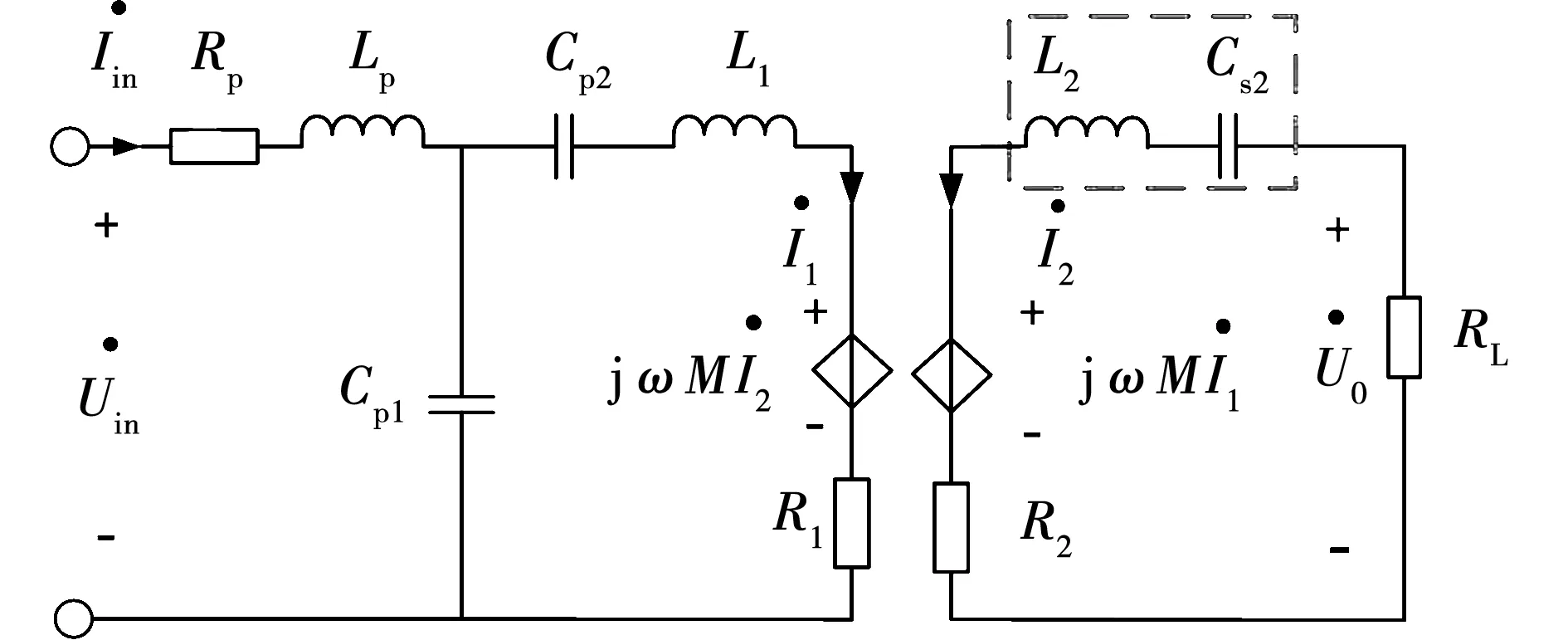
图3 LCC-S补偿等效电路图Fig.3 Equivalent circuit diagram of LCC-S compensation
所以,LCC-S补偿参数工作条件为
(7)
输出电压Uo-LCC/S为
(8)
是双LCC补偿电路输出电流的ωLs倍。
考虑寄生参数的影响,输出电压Uo、输入电流Iin和效率ηLCC-S分别为:
(9)
(10)
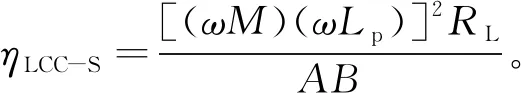
(11)
式中:A=Rp(ωM)2+[R1Rp+(ωLp)2](RL+R2);B=R1(RL+R2)+(ωM)2。
1.3 自动切换充电模式的工作原理
混合补偿拓扑如图4所示,一次侧为LCC补偿结构,二次线圈感应出恒定电压。为了实现充电模式的切换,二次侧引入了开关K1和K2。K1、K2闭合,由补偿电感Ls、补偿电容Cs1和Cs2构成二次侧LCC补偿网络,进行恒流充电。当充电电压等于恒压模式额定电压时,即Uout=Uo-LCC/S=Un时,K1、K2断开,补偿网络切换为LCC-S结构,由Cs2和Cs3完全补偿L2和Ls,进行恒压充电。而且,因L2和Cs2组成的等效电感Leq2和补偿电感Ls相等。所以,Cs1=2Cs3。为了避免因电容Cs3两端电压不为0,开关K1闭合出现短路,在Cs3支路串联了开关K3。在恒流模式,K3断开;在恒压模式,K3闭合。K3与K1、K2互锁,提高了系统的充电安全性。

图4 混合补偿拓扑图Fig.4 Hybrid compensation topology graph
2 基于互感识别的移相控制方法
两侧线圈发生偏移,互感减小,由式(3)和式(8)可知,双LCC补偿电路的输出电流Io和LCC-S补偿电路的输出电压Uo都将会随之线性减小。为了在较大偏移范围内都可以输出额定充电电流和电压,本文提出了如图5所示的移相控制方法。其中,地面侧逆变器为单相电压型全桥逆变电路,耦合补偿网络采用1.3节设计的混合补偿拓扑,车载侧整流器为电容滤波的单相不可控整流电路。

图5 移相控制方案图Fig.5 Phase shift control scheme diagram
逆变器的输出电压基波有效值Up表达式为
(12)
式中:E为直流源电压;α为移相角;β为死区角。
整流滤波电路输入电压Ur、电流Ir和输出电压UB、电流IB的关系[7]为:
(13)
且设定恒流模式额定充电电流IBn对应整流器输入电流Irn,恒压模式最小充电电流IBmin对应整流器输入电流Irmin。
为了移相调节逆变器输出电压Up,首先使用电流传感器检测得到逆变器输出电流Ip,再经过带通滤波器和信号调理电路,将其输入到DSP信号处理器中。之后,根据电流Ip和互感的一一对应关系,自动识别出实际的互感M实。
在实际应用中,传输线圈通常由利兹线绕制而成,线圈损耗电阻很小,为毫欧级电阻。而补偿电感的品质因数一般大于103,而补偿电容的等效串联电阻ESR更小,往往忽略不计。根据仿真和实验电路参数,考虑寄生损耗,可得到双LCC补偿电路输出电流Io与互感M和负载电阻RL的关系如图6所示。

图6 双LCC输出电流与互感和负载电阻关系图Fig.6 Relationship between output current of double LCC and mutual inductance and load resistance
可以看出,双LCC输出电流与互感仍基本为线性关系,系统中有功损耗对输入输出电流和互感的关系影响很小。为了方便理解,以下按理想电路进行分析。由能量守恒定理可知
UrIr=UpIp。
(14)
在恒流充电模式,结合1.1节的分析可得
(15)
式中Upn为设定的逆变器初始输出电压。
所以,根据检测到的电流值Ip,可得到实际互感为

(16)
由于每次开始充电时,电池的状态不一定相同。所以式(16)中的等效电阻RL也为变量,互感M为Ip和RL的二元函数。因此,在车载整流滤波电路前连接控制电阻Rc和控制开关S1、S2。在互感识别过程中,S1闭合,S2断开,上述分析中的RL=Rc,为固定值。所以,根据逆变器输出电流Ip的大小即可得到不同偏移状态的实际互感M实。
那么,为了输出额定电流,由式(3)可知逆变器输出电压Up应为
(17)
再根据式(12)调节移相角α,使得逆变器输出电压等于Up-M。当检测到地面侧逆变器实际输出电流Ip与所需电流Ip-M之间存在较大误差时,α进行迭代。当Ip达到误差允许范围内时,α自我保持。此时,对应车载侧Io=Irn,S1断开,S2闭合,输出额定充电电流IBn,开始恒流充电。随着电池等值电阻RB的增加,充电电压不断增大,当UB=UBn时,进入恒压充电模式。在恒压模式,随着电池等值电阻RB的增加,充电电压UB基本不变,充电电流IB不断减小。当IB=IBmin时,S1闭合,S2断开。而且,此时对应地面侧Ip等于Ipmin,自动关断驱动脉冲和地面侧电源,停止充电,即有
(18)
3 仿真与实验结果
3.1 仿真分析
为了分析混合补偿拓扑设计方案的可行性,结合硬件元器件的工艺和应用水平,考虑寄生参数,在MATLAB/Simulink仿真环境中搭建了如图7所示的系统仿真模型。其中,Inverter子模块为全桥逆变电路,输出频率为85 kHz的交流方波电压。设定恒流输出为5 A,恒压输出为200 V,参数设计如表1所示。并且,通过使用LCRTH2827A测量仪来测量耦合线圈和补偿电感/电容的实际值和寄生电阻。

表1 系统参数表
为了模拟在充电过程中电池等效电阻RB的增加,采用了受控电流源,控制量为自身电压,控制系数g为1/(20+400×t),仿真时间t设置为0.2 s,等效电阻RB从20 Ω增加到100 Ω。仿真算法设置为ode23tb,并且将Solver reset method设置为robust。

图7 系统仿真模型图Fig.7 System simulation model diagram
图8所示为充电电压和充电电流的仿真波形图,系统可以实现先恒流输出后恒压输出。随着等效电阻的增加,在恒流模式,充电电流IB基本保持为5 A;在恒压模式,充电电压UB基本保持为200 V。在t=0.056 s时,实现了充电模式的平稳过渡,电路中没有出现电流电压尖峰,充电电压的暂态最大波动率仅为0.7%。

图8 充电电压和电流的仿真波形图Fig.8 Simulation waveform of charging voltage and current
3.2 实验验证
为了验证系统方案的可行性,搭建了恒流输出5 A,恒压输出200 V的无线充电系统实验样机。采用Chroma品牌的62050H-600直流电源,逆变电路开关器件选用IMZ120R045M1型号的MOSFET,输出交流电压的频率为85 kHz,车载侧整流二极管为SCS220AGHR,耦合线圈采用不含铁氧体的圆形磁盘结构。按表1所示的参数设计补偿器件,补偿电容采用EPCOS/TDK薄膜电容,补偿电感采用铁硅铝磁环电感。地面侧DSP(TMS320F28335)处理器进行移相控制,车载侧DSP输出半导体开关控制信号。通过调节电子负载输出直流电阻的大小来模拟实现充电过程中充电电池等效电阻RB的不断变化。
3.2.1 切换恒流恒压充电模式方案可行性的验证
切换模式的暂态波形图如图9所示,在恒流充电模式,开关K1和K2闭合,K3断开,通过调节电子负载输出的直流电阻阻值,充电电流IB基本保持为5 A,充电电压UB不断增大。当充电电压UB达到200 V时,即充电电压UB等于了额定电压UBn时,开关K1和K2的控制信号跳变为了低电平,开关K3的控制信号跳变为了高电平,K1和K2断开,K3闭合,补偿拓扑从双LCC结构可靠安全地切换为了LCC-S结构。同时,充电电压UB和充电电流IB只出现了略微的减小,没有出现强烈的波动,充电电压的波动率仅有3.75%。而且,充电电压和电流都可以快速地恢复到稳态,实现了充电模式的稳定切换,开始恒压充电。
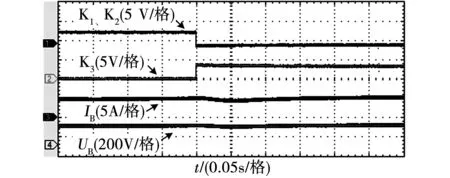
图9 切换模式暂态波形图Fig.9 Switching mode transient waveform
3.2.2 恒流/恒压输出稳定性的验证
在恒流模式下,充电电流和电压波形如图10所示。当等效电阻RB为10 Ω时,充电电流IB为4.9 A;当等效电阻RB为20 Ω时,充电电流IB为4.78 A。电流变化率仅为2.45%,基本保持恒定。
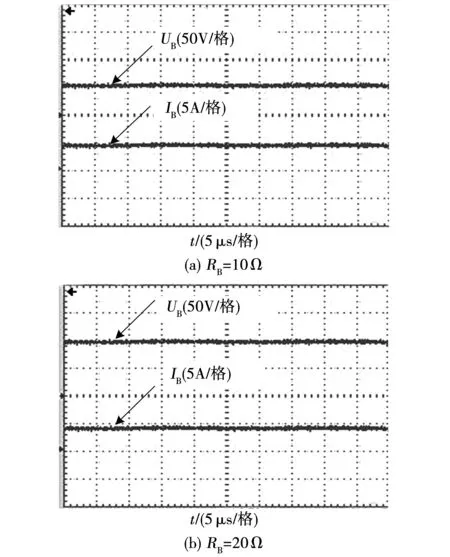
图10 恒流模式充电电流和充电电压波形图Fig.10 Waveform of charging current and voltage in constant current mode
在恒压模式下,充电电流和电压波形如图11所示。当等效电阻RB为50 Ω时,充电电压UB为202.5 V;当等效电阻RB为100 Ω时,充电电压UB为209 V。电压变化率仅为3.21%,基本保持恒定。
3.2.3 移相控制方法有效性的验证
当两侧线圈偏移距离d为100 mm时,驱动脉冲u1~u4的波形和充电电流IB和电压UB的波形分别如图12和图13所示。如果不进行移相控制,初始导通角θ为0.325π,充电电流IB为3.25 A。经过移相控制之后,导通角θ增加为0.66π,充电电流IB为5.2 A,基本恢复到了额定值。其中,电池等值电阻RB为最小等值电阻Rmin,设置为10 Ω,充电电压UB分别为32.2 V和51.5 V。其他不同偏移距离的实验数据如表2所示,实验结果表明采用基于互感识别的移相控制方法,在较大偏移范围内,系统都能基本以额定电流开始充电。
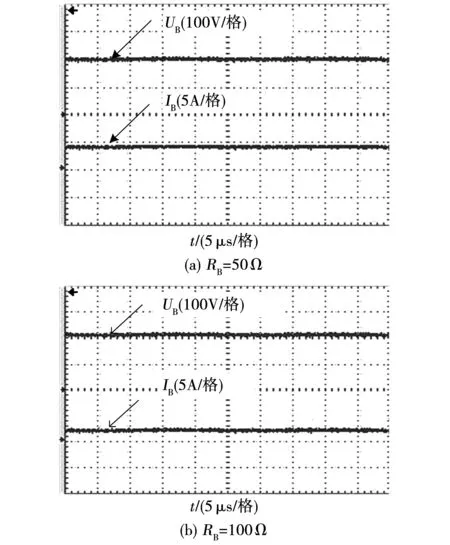
图11 恒压模式充电电流和充电电压波形图Fig.11 Waveform of charging current and voltage in constant voltage mode

表2 不同偏移距离的实验数据表

图12 发生线圈偏移的驱动脉冲波形图Fig.12 Driving pulse waveform after coil offset

图13 发生线圈偏移的充电电流和充电电压波形图Fig.13 Waveform of charging current and voltage after coil offset
4 结 论
通过对双LCC和LCC-S补偿电路的输出特性分析,结合电感电容的工作特性和系统安全稳定性,设计了基于LCC-LCC/S混合补偿网络的无线充电系统方案。通过自动切换副边补偿电路,系统可以安全平稳地实现恒流恒压充电模式的切换,不会对电路器件产生较大的电流/电压冲击,充电电流和电压随电池等值电阻的变化率相对较低,可以满足电动汽车的充电要求。在此基础上,为了使系统在较大的偏移范围内都可以实现额定电流和电压充电,提出了根据互感和原边逆变器输出电流的内在对应关系进行互感自动识别,从而实现移相调节逆变器输出电压的方法。该方法根据电路参数之间的关系,原副边分别控制,不需要原副边之间的控制环,省去了无线通信的环节。搭建实验样机,实验结果表明线圈偏移量在0~160 mm的范围内,系统的充电电流和电压可以基本保持额定值。

