七阶电力系统混沌振荡的动态面滑模控制

王江彬， 刘凌， 刘崇新

(西安交通大学 电气工程学院，西安 710049)

0 引 言

电力系统混沌振荡因其对整个系统稳定性构成挑战，因此对其进行控制就显得尤为必要[1-6]。针对电力系统混沌控制问题，研究最多的模型当属二阶电力系统模型[7-11]。也有众多混沌控制方法针对四阶电力系统模型。具体而言，文献[12-18]分别针对该系统提出了精确反馈线性化控制、自适应反馈控制、固定时间动态面高阶滑模控制、快速固定时间非奇异终端滑模控制、固定时间积分滑模控制以及更为实用化的协同控制。可以看出，目前人们仍然主要研究一些低阶电力系统模型。从控制的角度来说，这些模型均是比较简单的。

对于电力系统动力学模型而言，模型建立过程考虑的因素越全面，也就越能表征实际电力系统的运行特点，最终建立的模型必然也会越复杂。由于实际工程中的电力系统是典型的高维强耦合的复杂动力学系统，因而从实践的角度来说，控制更为复杂的电力系统模型就显得更为必要。著名的七阶电力系统模型是比较复杂的模型[19-22]，其参数耦合关系及每个参数物理意义详见文献[19-22]。由于模型本身的复杂性所致，对其进行控制就比较困难。文献[23]针对该系统的混沌控制问题提出了固定时间协同控制，然而所设计的控制输入包含受控系统函数的导数，这增加了工程实施的难度。另外，对于这一复杂系统仍然有必要提出新的控制方法。

鉴于此，研究了七阶混沌电力系统的控制问题，并将混沌控制问题最终归结为三个具有严格反馈形式的子系统的镇定问题。对于严格反馈系统，可以设计反推控制输入，然而反推控制存在“复杂性爆炸”问题[24-25]，即控制器设计过程需要对虚拟控制输入求导，因而设计的控制输入中必然包含受控系统函数的导数，这增加了控制器的复杂性，而动态面控制作为反推控制的进一步发展，其可以很好地解决这一问题[26-27]。另外，由于系统特点所致，引入滑模控制方法能够减少控制器设计的步骤，因此本文利用动态面控制并结合滑模控制方法针对七阶混沌电力系统设计了动态面滑模控制输入。

1 电力系统模型及混沌动力学分析

首先构建受控电力系统动力学模型，并对系统中的混沌振荡进行分析。考虑著名的七阶电力系统模型[19-22]，该系统模型对应的电路系统是一个典型三母线系统，包括发电机母线1、负载母线2以及无穷大母线3。图1中去掉“储能装置1”以及“储能装置2”模块的电路图为七阶电力系统的原有电路系统。为了进行控制器设计，为该系统引入两台储能装置，其中一台储能装置接在发电机母线处，用于调节该母线处的有功功率；另外一台储能装置接在负载母线处，用于调节该母线处的有功及无功功率。这样电力系统成为受控系统，其电路接线图如图1所示，图中与正文相同字母表示的含义相同。

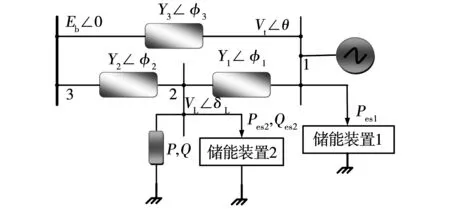
图1 受控七阶电力系统的电路接线图Fig.1 Circuit diagram of the controlled seven-dimensional power system

图1中，Pes1表示储能装置1从发电机母线吸收的有功功率，Pes2及Qes2表示储能装置2从负载母线吸收的有功功率及无功功率。而七阶电力系统模型中发电机母线处功率量Pm表示机械输入功率，负载母线处功率量P、Q分别表示提供给负载母线的有功功率及无功功率。考虑到这6个功率量表示的物理含义，从而将3个功率量Pes1、Qes2、Pes2与七阶电力系统模型建立耦合关系，并引入储能装置的动力学模型[28]，最终建立的受控十阶电力系统耦合动力学模型表述为

(1)

系统(1)中，除了Kpes1、Kqes2、Kpes2及Tes表示控制装置的常值参数之外，系统的其他常值参数均为七阶电力系统的常值参数。这其中除了重要分岔参数Pm=1.363，电力系统的其他参数取值及其初始值均引自文献[23]。储能装置动态系统的初值取为：Pes1(0)=0；Qes2(0)=0；Pes2(0)=0。在控制输入投入运行之前，电力系统中出现混沌振荡，系统状态在相图上表现为图2所示的奇怪吸引子。

图2 七阶混沌电力系统相图Fig.2 Phase portrait of the seven-dimensional chaotic power system

2 混沌控制器设计

为了控制系统(1)的混沌振荡，这里为其设计混沌控制输入upes1、uqes2及upes2来抑制这种混沌行为。

控制输入upes1的作用是使电力系统恢复到同步运行状态，控制输入uqes2的作用是使电力系统负载母线电压的相角恢复到额定值0，而控制输入upes2则可以使电力系统负载母线电压的幅值恢复到额定值1。为此，控制目标设定为(δm,sm,δL,VL)=(0,0,0,1)，系统输出确定为y1=δm，y2=δL，y3=VL。这样，混沌电力系统(1)的控制问题实质上就成为一个具有多输入多输出的高维强耦合的复杂动力学系统的控制问题。由于所研究的系统模型比较复杂，因此在控制器设计时需要观察输入量与输出量之间的对应关系，并通过输入与输出之间的关联将整个复杂动力学系统肢解为比较简单的子系统来进行控制器设计。利用这种思路可以将电力系统(1)的混沌控制问题归结为三个具有严格反馈形式的子系统的镇定问题，这样就可以利用动态面滑模控制方法控制各个子系统并为其设计对应的控制输入。

2.1 第一个控制输入的设计

为了使整个受控电力系统(1)恢复到同步运行状态需要设计控制输入upes1，由于该控制输入对应的输出为y1=δm，考虑由系统(1)的前三个方程构成的子系统的控制问题。注意到该子系统具有严格反馈形式，因此可以应用动态面控制方法对其进行控制。按照动态面控制方法设计控制器时，设计步骤必然包含三步。为了减少控制器设计步骤，并简化稳定性分析的复杂性，引入滑模控制方法并设计滑模面为

σ=sm+k·(δm/ωB)。

其中k为正的常数。

定义滑模面后，整个动态面滑模控制输入upes1的设计过程包含两步。

第1步：定义第一个动态面S1=σ，则动态面S1满足的动态方程为

(2)

为稳定动态面S1，选择虚拟控制输入

(3)

(4)

第2步：定义第二个动态面S2=Pes1-Pes1d，则该动态面S2满足的动态方程为

(5)

为稳定动态面S2，并使其收敛至0，设计最终的控制输入upes1为

(6)

这样，就完成了控制输入upes1的设计过程。

2.2 第二个控制输入的设计

为了控制负载母线电压的相角需要设计控制输入uqes2，由于该控制输入对应的输出为y2=δL，那么将系统(1)的倒数第三个方程和倒数第四个方程构成的系统作为一个独立的子系统，注意到它也具有严格反馈形式，因此可以为其设计动态面控制输入。对于该子系统，动态面控制输入uqes2的设计过程包含两步。

第1步：定义第三个动态面S3=δL，则该动态面S3满足的动态方程为

f(·)-Qes2/q1。

(7)

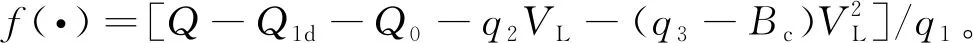
为稳定动态面S3，选择虚拟控制输入

(8)

(9)

第2步：定义第四个动态面S4=Qes2-Qes2d，则该动态面S4满足的动态方程为

(10)

为了稳定动态面S4，并使其收敛至0，设计最终的控制输入uqes2为

(11)

这样，就完成了控制输入uqes2的设计过程。

2.3 第三个控制输入的设计

为了控制系统负载母线电压的幅值需要设计控制输入upes2，由于该控制输入对应的输出为y3=VL，那么可以将系统(1)的最后两个方程构成的系统作为一个独立的子系统，注意到它也具有严格反馈形式，因此也可以利用动态面控制方法对其进行控制。对于该子系统，动态面控制输入upes2的设计过程包含两步。

第1步：定义第五个动态面S5=VL-1，则动态面S5满足的动态方程为

g(·)-(1/p2)Pes2。

(12)

为稳定动态面S5，选择虚拟控制输入

(13)

(14)

第2步：定义第六个动态面S6=Pes2-Pes2d，则该动态面S6满足的动态方程为

(15)

为了稳定动态面S6，并使其收敛至0，设计最终的控制输入upes2为

(16)

这样，就完成了控制输入upes2的设计过程。

至此，通过控制器设计就得到了三个控制输入的表达式。观察控制输入(6)、式(11)以及式(16)的最终表达形式，可以看出控制输入中均不包含受控系统函数的复杂导数项，形式更为简洁，因而本文控制方法比文献[23]的固定时间协同控制方法更易于工程实施。经过上述控制器设计过程，得到的整个受控电力系统最终等价于由式(1)、式(4)、式(9)以及式(14)的动力学方程组成的十三阶动力学系统。

3 闭环系统稳定性分析

下面给出受控闭环电力系统稳定性证明过程。

首先定义3个变量：

(17)

将式(17)的变量与所定义的6个动态面变量相结合，可以得到9个误差变量：

(18)

对于受控的闭环系统而言，可以写出式(18)中各个变量满足的动态方程。

结合式(2)、式(3)、式(5)、式(6)，可得闭环系统动态面S1与S2的动态方程表述为：

(19)

结合式(7)、式(8)、式(10)、式(11)，可得闭环系统动态面S3与S4满足的动态方程表述为：

(20)

结合式(12)、式(13)、式(15)、式(16)，可得闭环系统动态面S5与S6满足的动态方程表述为：

(21)

而误差变量z1、z2及z3满足的动态方程为：

(22)

为了进行稳定性分析，构造李雅普诺夫函数

考虑式(19)、式(20)、式(21)、式(22)，可得该函数关于时间的导数为

|z1|M1+|z2|M2+|z3|M3。

(23)

考虑到不等式：

其中：ξ1、ξ2及ξ3表示正的常数。

则式(23)可以表述为

(24)

针对式(24)，令参数满足不等式条件：

(25)

则可得

-2rV+M。

(26)

求解式(26)的微分方程不等式可得

则可以得

(27)

由式(27)可知：系统能够实现一致终结有界稳定，并且在M1、M2及M3一定的情况下，可以通过调节参数ξ1、ξ2、ξ3及r的值来使得控制误差尽可能小。由式(25)可知，r的值可以通过调节控制参数k1、k2、k3、k4、k5、k6的值进行设定，而ξ1、ξ2、ξ3的值可以通过调节τ1、τ2、τ3的值进行设定。

4 控制效果数值仿真及分析

为证实所设计控制器的有效性，利用MATLAB对控制效果进行数值仿真验证。控制参数取值为：Kpes1=1；Kqes2=1；Kpes2=1；Tes=1；k=10；k1=15；k2=15；k3=15；k4=15；k5=15；k6=15；τ1=0.01；τ2=0.01；τ3=0.01。式(4)、式(9)及式(14)中滤波器的状态变量Pes1d、Qes2d及Pes2d的初始值选取为：Pes1d(0)=0；Qes2d(0)=0；Pes2d(0)=0。在电力系统运行过程中，设定所设计的控制器在第10 s投入运行，所得到的控制效果仿真图如图3～图7所示。图3给出了控制器投入运行以后，由式(18)定义的9个误差变量的时域波形，由该图可得每个误差变量都收敛至0，这证实对受控闭环系统稳定性证明过程的正确性。

图3 误差变量时域波形Fig.3 Time responses of the error variables

图4给出了七阶混沌电力系统在控制器作用下的时域波形，该图说明每个状态变量均能够由混沌振荡状态恢复到平衡态，从而证实所设计控制器的有效性。整个受控电力系统最终等效于一个十三阶动力学系统。

图4 控制器作用前后七阶电力系统时域波形Fig.4 Time responses of the seven-dimensional power system before and after controllers are put into operation

图5给出了该等效十三阶系统每个状态变量的时域波形，该图表明受控电力系统的每个状态变量均恢复到平衡态，从而使整个受控电力系统完全恢复到稳定运行状态。图6给出了受控电力系统由混沌状态演化为不动点的演化过程图，正如该图所示，控制器运行之前电力系统状态在相空间中表现为奇怪吸引子，控制器投入运行后整个系统的状态由相空间中原来的奇怪吸引子经特定的演化轨线逐渐演化为平衡态不动点，系统奇怪吸引子消失，七阶电力系统恢复稳定。图7为所设计控制输入的时域波形，由于所设计的控制输入为连续控制律，因而控制输入是平滑波形。

图5 控制器投入运行后等效十三阶电力系统的时域波形Fig.5 Time responses of equivalent thirteen-dimensional power system under the designed controllers

图6 受控电力系统状态在相空间中的演化过程图Fig.6 Evolution process diagram of controlled power system state in phase space

图7 所设计的控制输入时域波形Fig.7 Time responses of the designed control inputs

5 结 论

1)通过对七阶电力系统模型引入储能装置的动力学模型，可以有效控制电力系统中的混沌振荡，这说明电力系统混沌振荡控制问题的本质是对电力系统有功功率以及无功功率的控制。

2)将复杂七阶混沌电力系统的控制问题最终归结为三个具有严格反馈形式的子系统的控制问题，并为其设计了对应的动态面滑模控制输入。经过动态面滑模控制器设计，受控电力系统本质上形成一个复杂的十三阶电力系统动力学模型，当控制器投入运行后，系统的十三个状态变量均恢复到平衡态，这时电力系统也就恢复到了稳定运行状态，从而有效控制了电力系统的混沌振荡。

3)由于对七阶电力系统模型进行化简就可以得到更为简单的四阶及二阶电力系统模型，因而七阶混沌电力系统的控制成功意味着再没有必要从确定性系统混沌控制的层面再来研究这些更为简单的电力系统动力学模型。本文对七阶混沌电力系统的控制思路可以延伸应用于解决更加实际的电力系统动力学模型的混沌控制问题。