永磁同步电机磁链修正无位置传感器控制
吴建华, 吴航
(浙江大学 电气工程学院,杭州 310000)
0 引 言
随着《中国制造2025》规划的出台,国家和政府明确强调要推动机器人和数控装备等创新产业的发展,其中,永磁同步电机因具有转矩大、精度高、效率高等优点而广泛应用于伺服设备,并且采取矢量控制策略可以使其具有类似直流电机磁链和转矩相互解耦的特性,可以单独对转矩或磁链进行控制,并且由于永磁体的存在,在电压允许的条件下,可以有效提高电机的输出转矩,因此永磁同步电机在工控设备领域得到了越来越多的应用和发展,是当前的研究热点之一。矢量控制方法对电机的位置精度提出了较高的要求,传统的永磁同步电机常采用有位置编码器获得位置信息,这不但提高了系统的成本,还增加了电机的体积,并对使用环境提出了较高的要求,而使用无位置传感器控制方法可以省去位置传感器,并针对电机特定的工作环境选择对应的无位置传感器控制策略。因此,无位置传感器控制策略的研究具有广阔的前景[1-4]。
内置式永磁同步电机无位置传感器控制策略在低速和中高速运行时常用的方法分别是高频注入法和反电势法,而表贴式电机在低速运行时由于凸极效应不明显往往采用IF控制方法。其中高频注入法主要包括脉振高频信号注入法、旋转高频信号注入法等[5-7],该方法需要利用内置式电机的凸极特性,因此不适用于表贴式永磁同步电机,而IF控制属于转速开环电流闭环的无位置控制方法,该方法可以有效解决表贴式电机的起动问题。反电势法主要包括滑模观测器算法、模型参考自适应算法等,该方法则利用电机的电压方程估算电机反电势,进而估算电机位置信息[8-15],其中,由于表贴式永磁同步电机电压方程的特殊性,电机转速可以直接由估算的反电势和电机磁链的比值获得,而实际的运行工况下,电机磁链是一个随工况变化的测量量,往往无法直接由固定的磁链幅值估算电机位置信息。
永磁同步电机在不同的运行工况下,温度、电流等参数的变化不仅会影响定子电感、电阻的大小,还会影响磁链幅值,因此电机在运行过程中磁链的变化不仅会严重影响对位置信息的估算,还会降低系统的稳定性甚至失控。此外,由于电机磁链本身就是一个测量量,当测量初值存在误差时,利用磁链观测电机转速时则会将误差直接引入到估算的转速和位置信息。磁链误差观测器根据电机的磁链方程,可以观测得到磁链的误差,通过磁链误差对磁链幅值进行在线修正,可以有效提高磁链幅值的准确性[16-19]。本文提出了一种带有磁链修正的滑模观测器(FC-SMO),通过重写磁链方程构建磁链误差观测器以获得磁链误差,并对永磁体磁链进行在线修正,进而根据滑模观测器估算的反电势和磁链修正值估算转速和位置信息。仿真与实验表明,本文所提出的方法能够有效估算电机磁链误差,在对磁链进行在线修正后可以准确估算出电机转速和位置,实现永磁同步电机的无位置传感器控制。
1 数学模型
表贴式永磁同步电机在静止两相坐标系α、β下的电压方程为
(1)
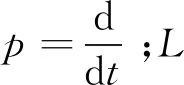
(2)
式中:ω为转子电角速度;ψf为永磁体磁链;θ为转子位置。
将式(1)改写为电流的状态方程,即
(3)
2 带磁链修正的滑模观测器
2.1 传统滑模观测器算法
基于式(3)所示的永磁同步电机电流状态方程,为了获得反电动势的估算值,传统滑模观测器的设计通常为
(4)

将式(3)和式(4)作差,可得定子电流的误差方程为
(5)
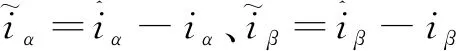
滑模面函数为
(6)
滑模控制律设计为
(7)
式中m为滑模控制律增益系数。
当观测器的状态变量到达滑模面后,根据等效控制原理,可得反电势估算值为
(8)
根据式(2),可得电机转速和位置估算值为
(9)
(10)
2.2 磁链误差观测器
电机磁链初值一般由测量获得,测量的精度会直接影响转速和位置的估算精度,此外,由于电机运行在不同工况下会存在一些扰动信号,使得定子电感、电阻以及永磁体磁链的幅值和角度发生偏移,此时,如果将磁链幅值看作常量,并利用式(9)和式(10)计算得到转子转速和位置,势必会出现偏差,严重时将会直接影响系统的稳定性,造成系统失衡。利用磁链误差观测器获得磁链误差并进行在线修正,将会提高电机转速和位置的估算精度。
根据图1可得定子磁链在两项静止坐标系下的表达式为
(11)

同理可得,实际定子磁链在两项静止坐标系下的表达式为
(12)
式中Δψα和Δψβ分别为两相静止坐标系下的磁链误差,其表达式为
(13)
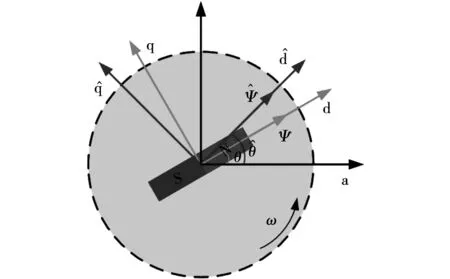
图1 定子磁链模型Fig.1 Stator flux linkage model
根据式(12)和电机定子磁链方程可得
(14)
根据上式,当定子磁链出现误差时,定子磁链微分方程可以表示为
px=Ax+Bu+Cd-Bff。
(15)

系数矩阵表达式为
(16)
当忽略电机定子电感磁链时,由式(11)可得
(17)
设计磁链误差滑模观测器如下,其结构框图如图2所示。
(18)
式中kψ为常系数。

图2 FC-SMO观测器结构框图Fig.2 Diagram of FC-SMO
当磁链误差观测器的状态变量在滑模面附近切换时,由式(13),定子磁链误差即为永磁体磁链误差,可以表示为
Δψ=msgn(z)+nz。
(19)
则实际磁链幅值和角度可由永磁体磁链经过式(19)和式(20)修正后得到,整个磁链修正无位置传感器控制框图如图3所示,即
(20)
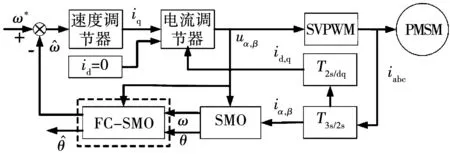
图3 FC-SMO无位置传感器控制框图Fig.3 Diagram of FC-SMO position sensorless control
转子位置可通过式(10)或下式获得:
(21)
2.3 稳定性分析
利用李雅普诺夫函数证明磁链误差观测器的稳定性,其表达式为
(22)
对上式的α分量求导可得
(23)
则存在m>0,使得
(24)

3 仿真分析
3.1 永磁同步电机无位置传感器控制系统
FC-SMO无位置传感器控制框图如图3所示,表1为永磁同步电机模型参数,搭建基于MATLAB/Simulink仿真以验证本文所提磁链修正方法的有效性,并对磁链存在误差下的修正过程进行了仿真分析。

表1 永磁同步电机样机参数
3.2 磁链扰动下转速和位置的跟踪性
为验证FC-SMO对磁链误差的修正能力,仿真设定电机转速为1 500 r/min空载运行,人为设定电机磁链为0.1 Wb作为磁链初值以验证本文所提磁链修正方法的有效性,如图4所示。图中:v和θ为电机实际转速和位置;vSMO和θSMO为未经修正的电机转速和位置;vFC-SMO和θFC-SMO为经过磁链误差观测器修正后的电机转速和位置;Δψα和Δψβ为αβ坐标系下的磁链误差;ψ为永磁体磁链幅值。由图4(a)可见,在电机磁链初值存在误差或扰动时,传统的滑模观测器转速和位置估算方法已无法跟踪实际转速和位置,电机估算转速和位置均存在较大误差,而经过磁链误差观测器修正的电机转速可以跟踪实际转速,具有较强的跟踪能力。经过磁链误差观测器修正后的永磁体磁链如图4(b)所示,在对磁链进行误差修正后,永磁体磁链由初始的0.1 Wb跟踪到实际的0.15 Wb。
为了进一步验证所提磁链误差观测器的有效性,设置初始磁链为0.2 Wb,由图4(c)和4(d),磁链误差观测器可以达到同样的效果。通过仿真研究,磁链初值误差在约±40%以内时利用本文所提方法可以收敛至实际磁链,由此可见,当电机磁链存在一定的扰动及误差时,本文所提磁链误差观测器可以对电机磁链进行修正,使其跟踪电机实际磁链,并使电机估算转速和位置跟踪电机实际转速和位置信息。

图4 转速、位置和磁链的跟踪性Fig.4 Tracking performance of speed position and flux linkage
3.3 反电势
增加磁链误差及扰动后无位置传感器控制反电势波形如图5所示,反电势波形仍具有较好的正弦性和稳定性。
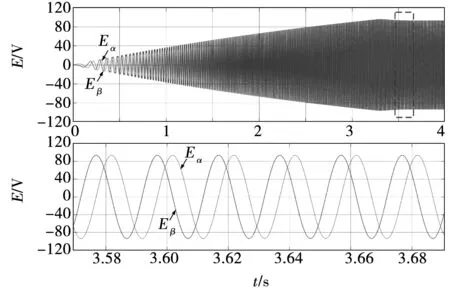
图5 反电势Fig.5 Back-EMF
4 实验验证
搭建dSPACE实验平台验证本文所提磁链修正方法的正确性,对表1的表贴式永磁同步电机进行实验研究,如图6所示。

图6 实验平台Fig.6 Experiment platform
永磁同步电机首先由IF控制方式起动,当电机转速升到200 r/min时,切换到FC-SMO控制方式运行。利用未经修正的磁链估算的电机转速和位置与实际值误差较大,系统无法在不同工况下稳定运行,在经过磁链修正后,系统稳定性显著改善。
永磁同步电机首先在500 r/min空载和负载运行测试,磁链初始值由反拖电机并根据式(9)计算获得,反拖转速为100 r/min,磁链计算结果约为0.153 Wb。由图7(a)可见,电机在空载稳态运行时,经FC-SMO对磁链修正后可以准确估算电机转速,估算位置略滞后于实际位置。反电势及估算磁链波形如图7(b)所示,图中Iabc为定子三相电流,E为反电势波形,磁链在dSPACE上位机界面读取数值为0.146 Wb。
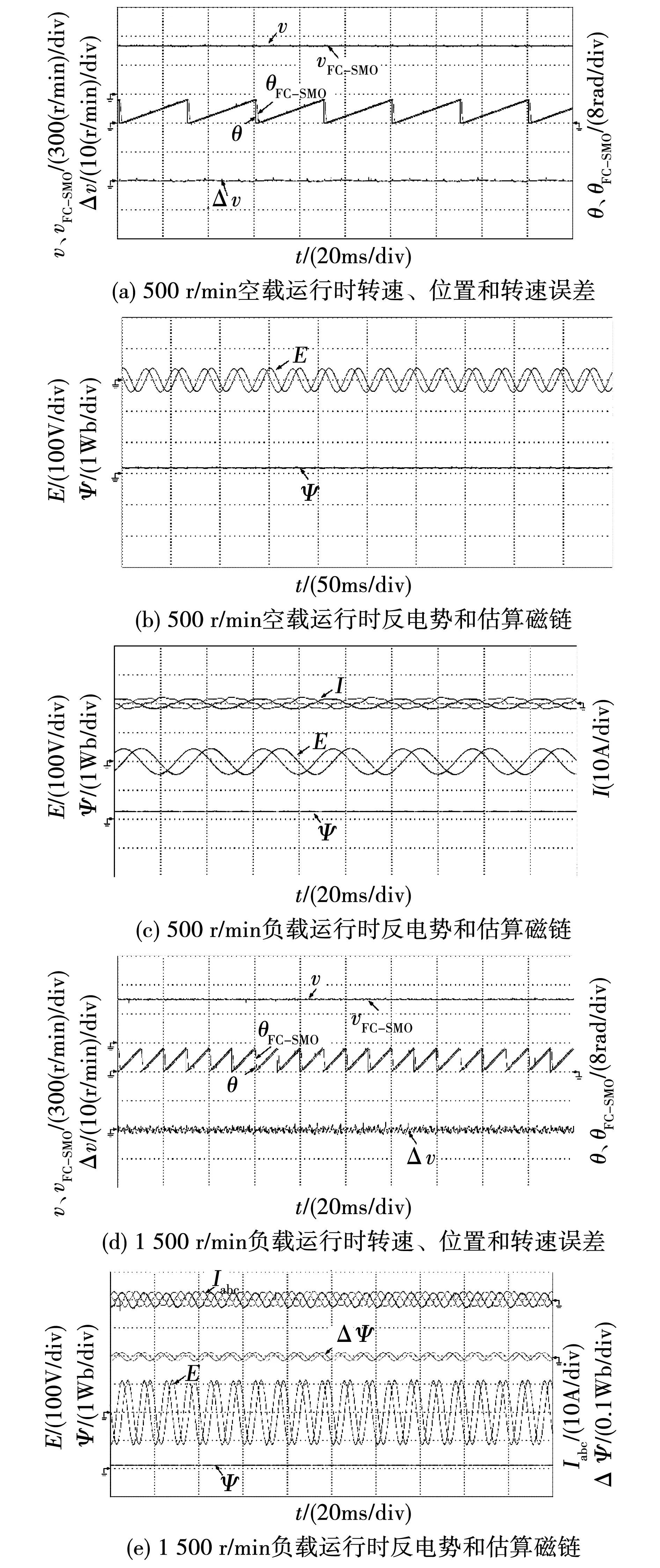
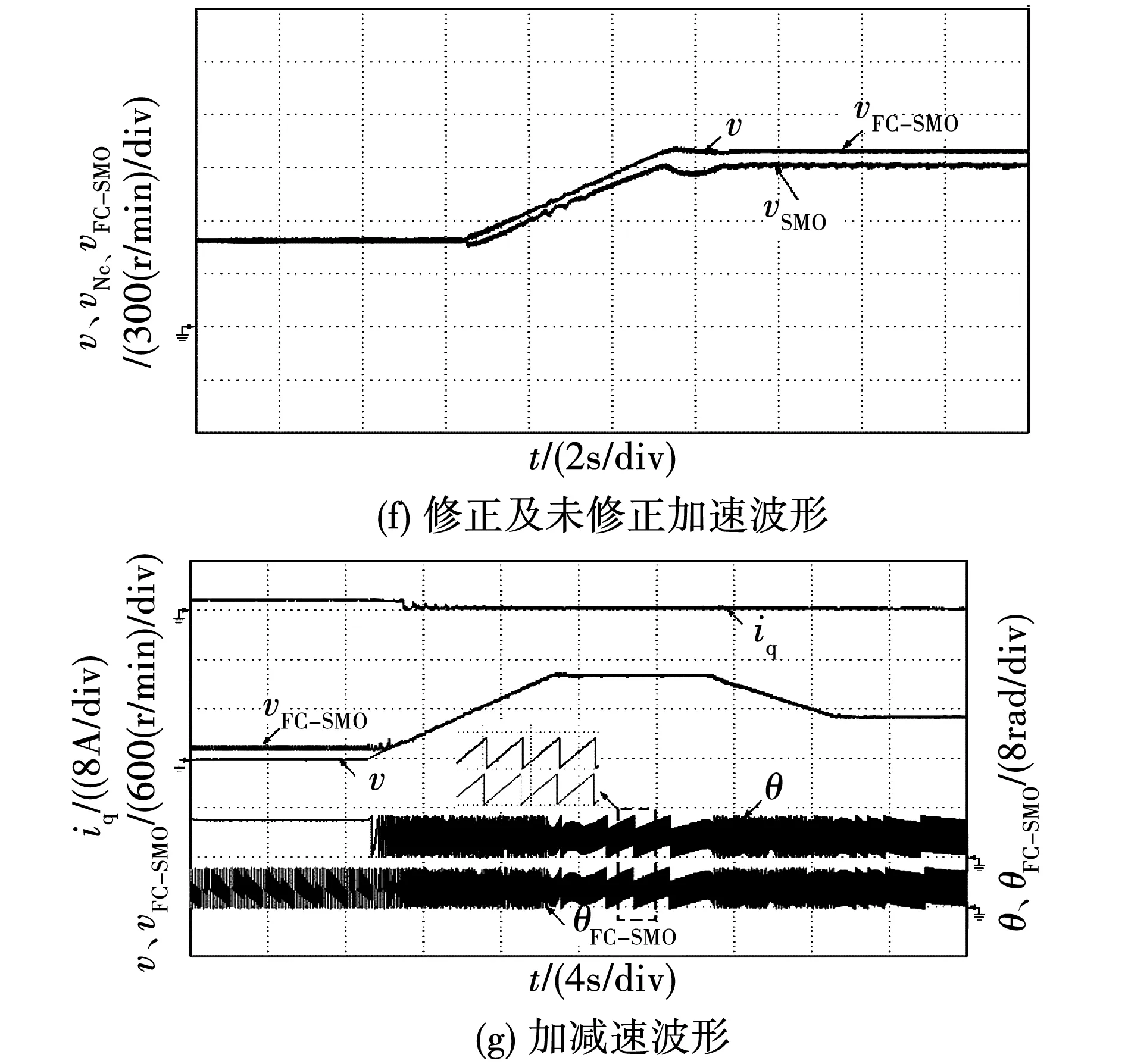
图7 实验波形Fig.7 Experiment waveforms
图7(c)为电机负载2 N·m运行时定子电流、反电势及磁链波形,负载运行时,定子电流约为2.2 A,反电势基本保持不变,此时磁链读数为0.141 Wb,由于电机负载运行,定子电流产生的磁场对电机磁链造成了干扰,而磁链误差观测器对磁链加以修正,使电机转速维持稳定。由实验可以看到,不同工况下电机磁链是不同的,需在线修正才能保证转速和位置的估算精度。
图7(d)为电机1 500 r/min负载3 N·m运行时转速和位置波形,转速提高后,转速误差略有增加,但仍能准确跟踪实际转速,图7(e)为该工况下反电势及估算磁链波形,磁链读数为0.137 Wb,转速提高时,电机铁耗增加,对磁链造成干扰,磁链在观测器的修正后仍能保持转速的准确跟踪。经实验验证,磁链初值与终值在约±30%误差范围内都能准确观测和修正。
图7(f)中为磁链固定为0.15 Wb时电机由300 r/min加速至1 000 r/min的转速波形,可见在电机转速为300 r/min时,磁链设置为0.15 Wb可以准确估算出实际转速,但是当电机加速至1 000 r/min后估算转速出现较大偏差,利用该转速和位置信息已无法控制电机正常运行,而经过修正的电机转速可以准确跟随实际转速,可见利用数学公式估算电机转速时进行磁链修正是非常必要的。
图7(g)为磁链初始值设置为0.19 Wb时电机由静止起动加速至1 000 r/min并加速回500 r/min的转速波形,由于磁链初值存在误差以及反电势估算不明显,电机在零速时估算出的电机转速存在约80 r/min的误差,在电机以IF控制起动后,转速达到100 r/min后,利用公式估算的电机转速和锁相环法估算的电机转速基本一致,IF控制和滑模观测器法的切换转速设置为250 r/min,转速切换成功后利用公式法估算的电机转速和位置控制电机时,加减转速可满足控制要求。实验中位置波形异常的原因是横坐标时间轴每格表示时间过大,采样数据点不足所致,当减小时间轴每格表示时间,位置信息即可恢复正常。
5 结 论
本文提出了一种带有磁链扰动修正的滑模观测器FC-SMO,通过重写定子磁链方程构建磁链误差观测器以获得磁链误差,并对永磁体磁链进行在线修正,进而根据滑模观测器获得的反电势和修正后的磁链值估算转速和位置,仿真和实验验证了方法的有效性,FC-SMO具有以下优点:
1)构建了磁链误差方程,通过磁链误差观测器获得磁链误差并对永磁体磁链进行在线修正,提高了转速和位置的估算精度。
2)通过磁链误差观测器构建磁链闭环控制,使传统的表贴式永磁同步电机转速估算方法适用于实际的无位置传感器控制。
3)由于磁链误差修正器的存在,拓宽了磁链初值的给定范围,使得磁链初值约在±30%的误差内即可准确估算电机位置信息,达到控制要求。

