港铁车轮与60E1钢轨单向伸缩调节器的接触分析

于开福

(中铁山桥集团有限公司, 河北 秦皇岛 066205)

轨道交通运输是中国最主要的运输方式。随着市场经济的快速增长，为了提高运输效率、节约成本以及提高乘客的舒适性，对钢轨一体化的要求更加严苛。在一些特殊的运输环境中，为了避免热胀冷缩对钢轨形成破坏，前人针对应用环境的不同，分别研究设计了应用于高铁、大桥以及地铁运输的钢轨伸缩调节器。钢轨伸缩调节器(简称为调节器)是组成高速铁路的重要轨道部件之一，是实现轨道现代化的一项重要技术措施。

钢轨伸缩调节器已广泛应用于国内很多城市的轨道交通工程，可有效避免长钢轨位移向道岔区的传递，保证高架线路道岔的安全正常工作。钢轨伸缩调节器的应用解决了随着科技发展、铁路提速而带来的超长无缝轨道路线铺设难题(即无缝线路的应力放散问题)。

钢轨单向伸缩调节器结构及实物如图1、图2、图3所示。钢轨伸缩调节器由基本轨、尖轨、扣件、轨撑板、弹性垫板、轨枕或轨道板、伸缩量标识等部件组成，调节器里侧为尖轨，外侧为基本轨，轨与轨之间采用扣件连接。当轨道发生热胀冷缩时，调节器中的尖轨与基本轨产生相对滑移，从而保证轨道整体形态的稳定。

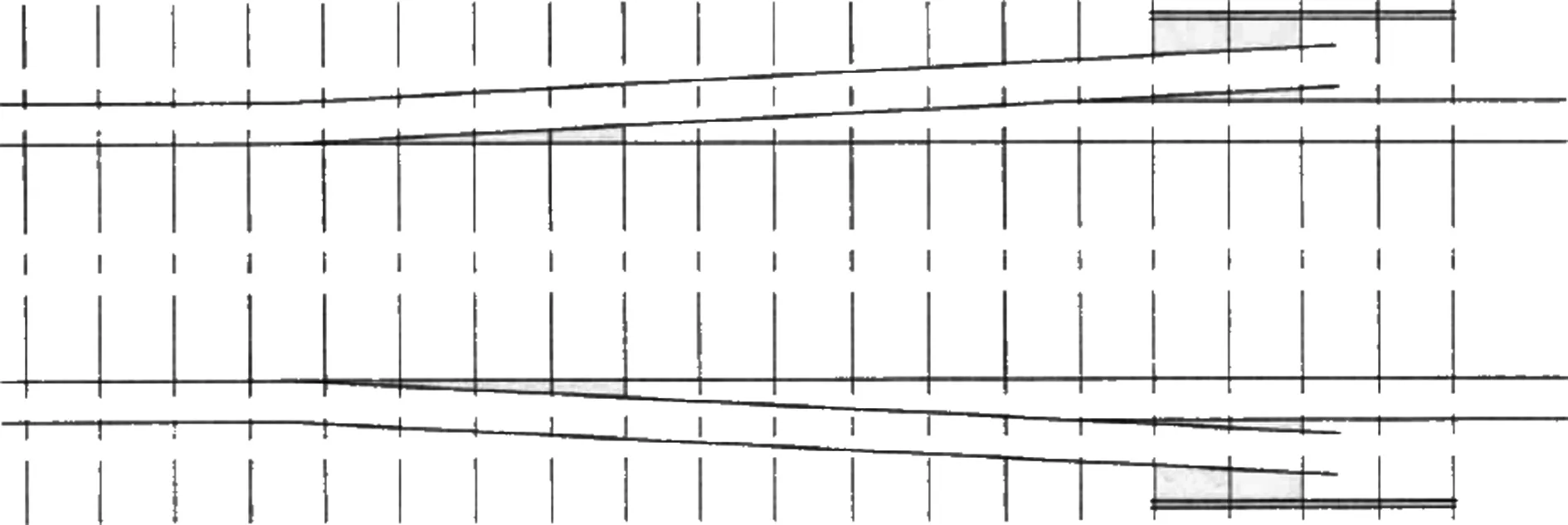
图1 钢轨单向伸缩调节器示意图

图2 钢轨单向伸缩调节器实物图

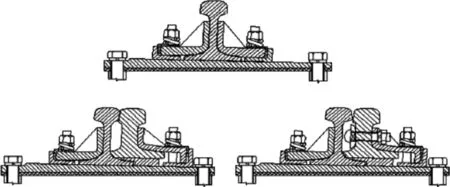
图3 钢轨单向伸缩调节器结构图

近年来，中外学者针对钢轨伸缩调节器应用中存在的问题做了大量的研究。一些学者对桥上梁端钢轨伸缩调节器进行了研究。王森荣通过对大跨度桥上梁端钢轨伸缩调节器及梁缝处抬轨装置的调研和现场实测，得出该区域轨道结构可能出现的病害，并分析了其成因[1]。何永昶系统计算分析了桥上钢轨扣件型式和伸缩调节器布置对轨-桥系统纵向相互作用的影响，并提出了钢轨扣件和伸缩调节器合理布置方案，研究结果表明：桥上铺设小阻力扣件可使钢轨制动力幅值略有减小，伸缩附加力最大值明显减小，挠曲力幅值有所减小，在主桥两端设置钢轨伸缩调节器对降低轨-桥系统纵向相互作用力效果最佳[2]。

许多学者从尖轨线型和温度等方面研究调节器的影响因素。文献[3]通过对各种尖轨刨切线型分析，得出结论：构造轨距及尖轨纵向位移引起的轨距变化主要受尖轨降低值影响；减小刨切线型的曲率半径，可减小尖轨刨切长度；曲线用调节器铺设于线路曲线半径较大的地段，有利于减小内外侧基本轨受力的差异。丁静波等研究了温度变化对钢轨伸缩调节器的影响，并建议在桥梁上使用调节器时使用梁轨一体化设计，不建议在曲线轨道路线上铺设调节器，在可能使用调节器的路段预留满足调节器使用的条件，避免后期铺设调节器而引发问题[4]。

还有大量专家通过分析调节器病害的原因，对新路线的设计提出相应的建议。王宏昌等通过研究发现在新线路的设计阶段，应做好统筹规划，避免在曲线路段铺设调节器，以增加轨道的铺设难度以及后期维护工作量[5]。许多学者对钢轨伸缩调节器进行动力特性试验,检测包括钢轨强度在内的大量内容，验证了该线路使用的双向曲线型钢轨伸缩调节器的合理性，对该调节器的性能优越性予以肯定[6-8]。大量研究人员通过对病害原因的分析，结合运营线路上病害整治施工的难度以及尽量减少对运营的干扰、降低施工风险和成本，制定切实可行的整治措施和设计优化方案。

探究不同情况下的车轮与调节器的接触，充分总结车轮与钢轨的接触规律，将有助于改善国内日渐庞大的铁路网络的运行状况，直接提高路段的使用寿命。并且，只有充分了解了钢轨上的薄弱环节的具体情况，才能在此基础上做出相应的预防与技术革新，且满足铁路运营日渐严苛的要求。

本文对港铁车轮与60E1钢轨单向伸缩调节器的接触情况进行有限元仿真计算，并通过仿真结果做出分析，总结了不同工况下港铁车轮与60E1钢轨单向伸缩调节器的接触情况变化规律，分析病害的产生原因，并提出合理建议。

1 单向伸缩调节器的有限元仿真计算

1.1 单向伸缩调节器有限元模型的建立

以60E1钢轨单向伸缩调节器上的一个具有典型特点的截面(图4)处的轮轨接触情况作为研究对象，应用有限元软件建立三维模型，进行仿真计算。

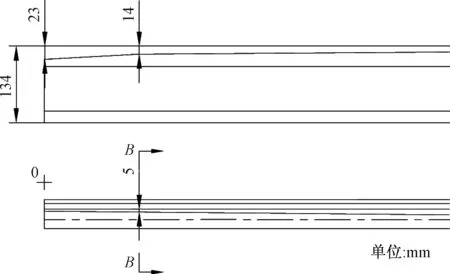
图4 60E1钢轨单向伸缩调节器的截面

图5所示为港铁车轮的几何外形图，通过几何外形图可知，车轮踏面是由许多不同曲率半径的曲线组合而成。

图5 港铁车轮几何外形图

图6为B截面处60E1钢轨单向伸缩调节器的几何外形图，港铁车轮将实现从基本轨向尖轨的移动。

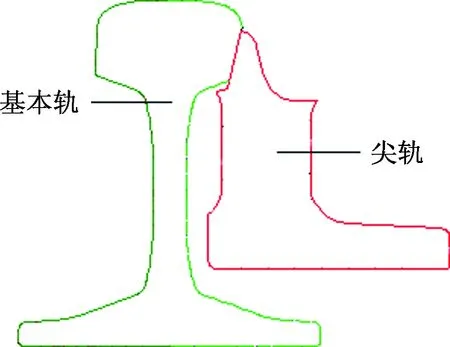
图6 截面的钢轨几何外形图

图7所示为通过钢轨与车轮的几何外形图建立的三维有限元模型，根据轮轨接触时的实际受力特点，与所学的知识相结合，可以将模型分为“接触区”和“非接触区”，在接触区附近区域有较大的接触应力，而非接触区域受力远小于接触区域。为了减少计算的时间成本，在不影响计算结果的前提下，建立模型时，只将接触区画为1×1的正六面体，非接触区为逐渐增大的六面体单元。

图7 轮轨接触有限元模型

1.2 材料属性

港铁车轮与60E1钢轨单向伸缩调节器材料应用如图8所示的双线性模型进行定义，在软件的参数设置中，材料力学性能中的弹塑性特性将依据该曲线进行参数设置。屈服极限为689.6 MPa，杨氏模量为205 000 MPa，硬化模量为20 500 MPa。

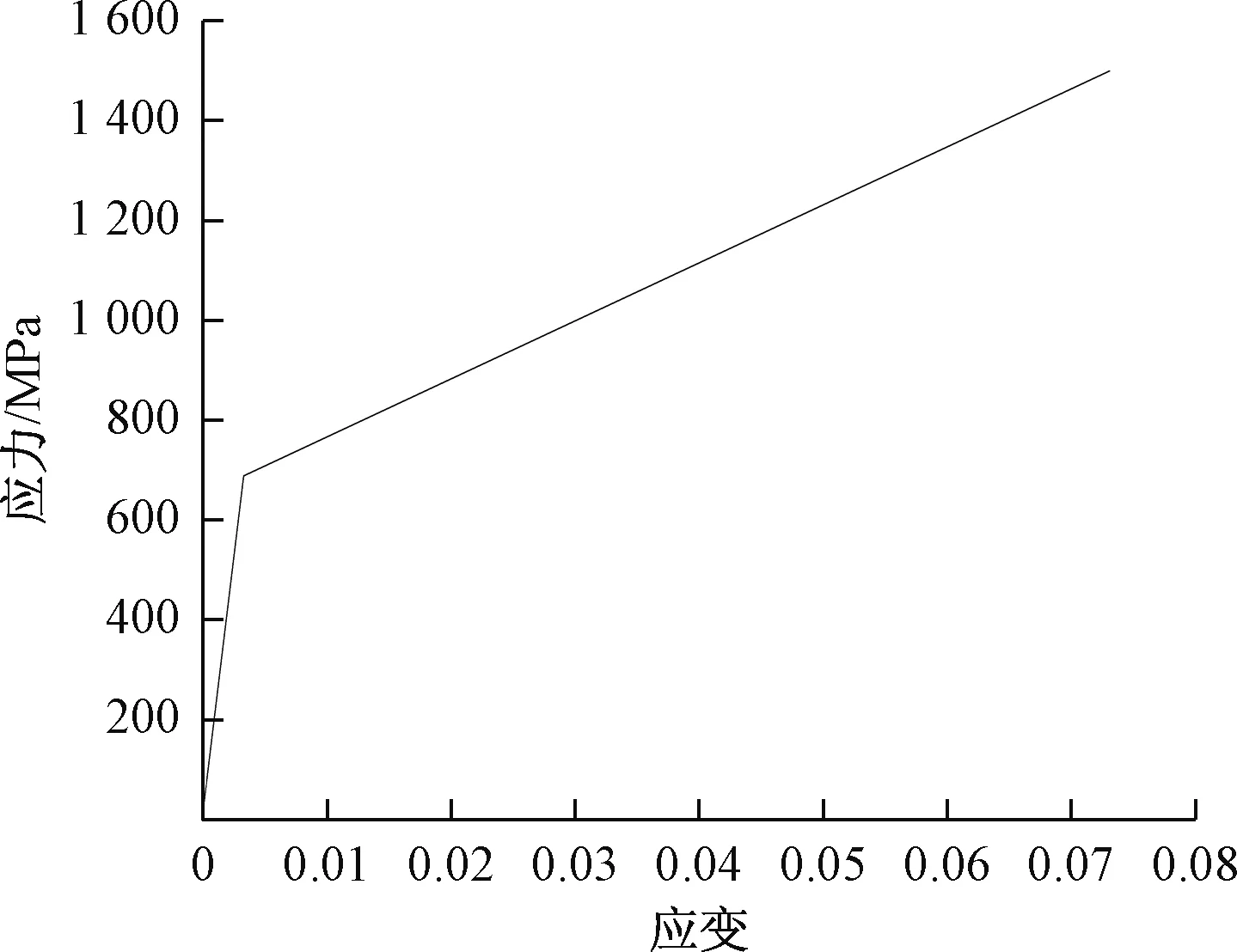
图8 双线性模型

1.3 载荷与边界条件

在有限元仿真计算中，在三维模型施加相应的约束，以模拟轮轨准静态接触状况。轮轨间的摩擦系数为0.3，在车轴的两端施加集中载荷，以模拟不同的轴重的影响。在轨底施加全约束；轮对只有一个垂向自由度，即沿垂向的移动，对3个方向的转动以及纵向和横向的移动进行约束。

2 计算结果分析

2.1 接触斑

2.1.1 横移量对接触斑的影响

因钢轨上的接触斑较之轮对更易于观察，以钢轨左轨上接触斑为研究对象。保持轴重不变是多少？将轮对左右横移，向左移动记为“-”，向右移动记为“+”，取-4、-2、0、+2、+4 mm 5个经常出现的横移量进行对比分析，以研究横移量对接触斑的影响。

将计算所得的接触斑列于表1中，由表1可知，接触斑呈现较规则的椭圆形，并且在对中位置时的面积最小为79.5 mm2，对中位置横移量为2 mm时相较于对中位置触斑面积均呈增加趋势，且增加量基本一致；横移量为4 mm时相较于横移量为2 mm时呈减小趋势。

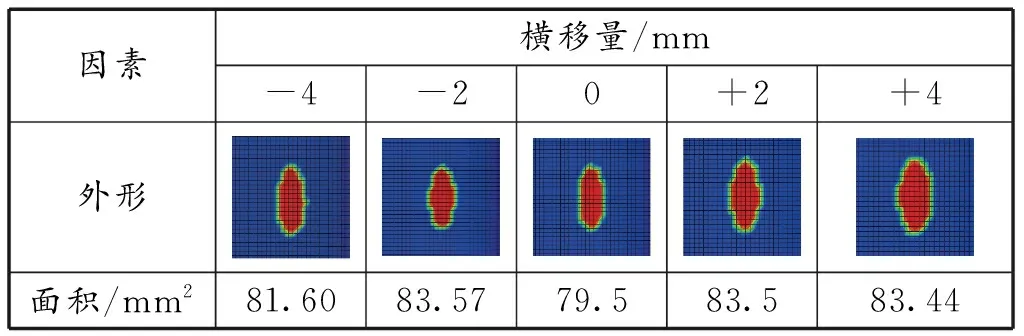
表1 不同横移量的接触斑

接触斑面积根据横移量的不同以对中位置为中心展现出对称变化。由于调节器基本轨的轨面是对称的，左移和右移具有对称的变化规律。接触斑面积差最大为4.07 mm2，相同的轴重工况，接触斑面积越大，每个节点的等效应力越小。横移量发生改变，接触斑面积显著变化，将加速车轮的磨耗。

2.1.2 轴重对接触斑的影响

在对中位置模型中，施加不同的轴重进行计算，以分析轴重对接触斑的影响。分别选取了16、18、20 t 3种轴重载荷进行计算，不同轴重时的接触斑形状与面积见表2。

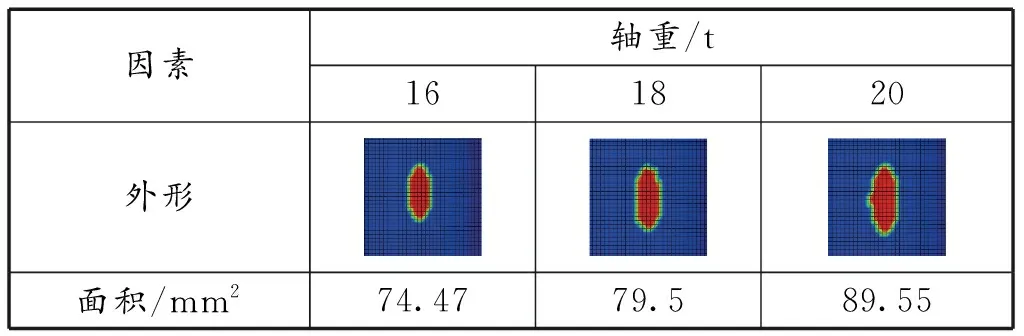
表2 轴重对接触斑的影响

从接触斑的外形可知，3种工况下的接触斑都呈现较为规则的椭圆形，随着轴重的增加，接触斑的外形逐渐变的“狭长”，即椭圆形的长轴增加，短轴减小。这是由于轴重的增加，使得车轮的塑性变形加剧。

接触斑的面积随轴重的增加而增大，18 t轴重相较于16 t轴重接触斑面积增加了6.75%，而20 t轴重相较于18 t轴重接触斑面积增加了12.64%。较大面积的接触斑有利于调节器的承载，但是对等效应力具有一定的影响。

2.2 等效应力

通过建立三维有限元仿真模型探究港铁车轮与60E1钢轨单向伸缩调节器的静态接触系统中左轨上的等效应力。经过计算，等效应力的分布情况大致相同，以横移量为4 mm时的计算结果为例，等效应力分布如图9所示。

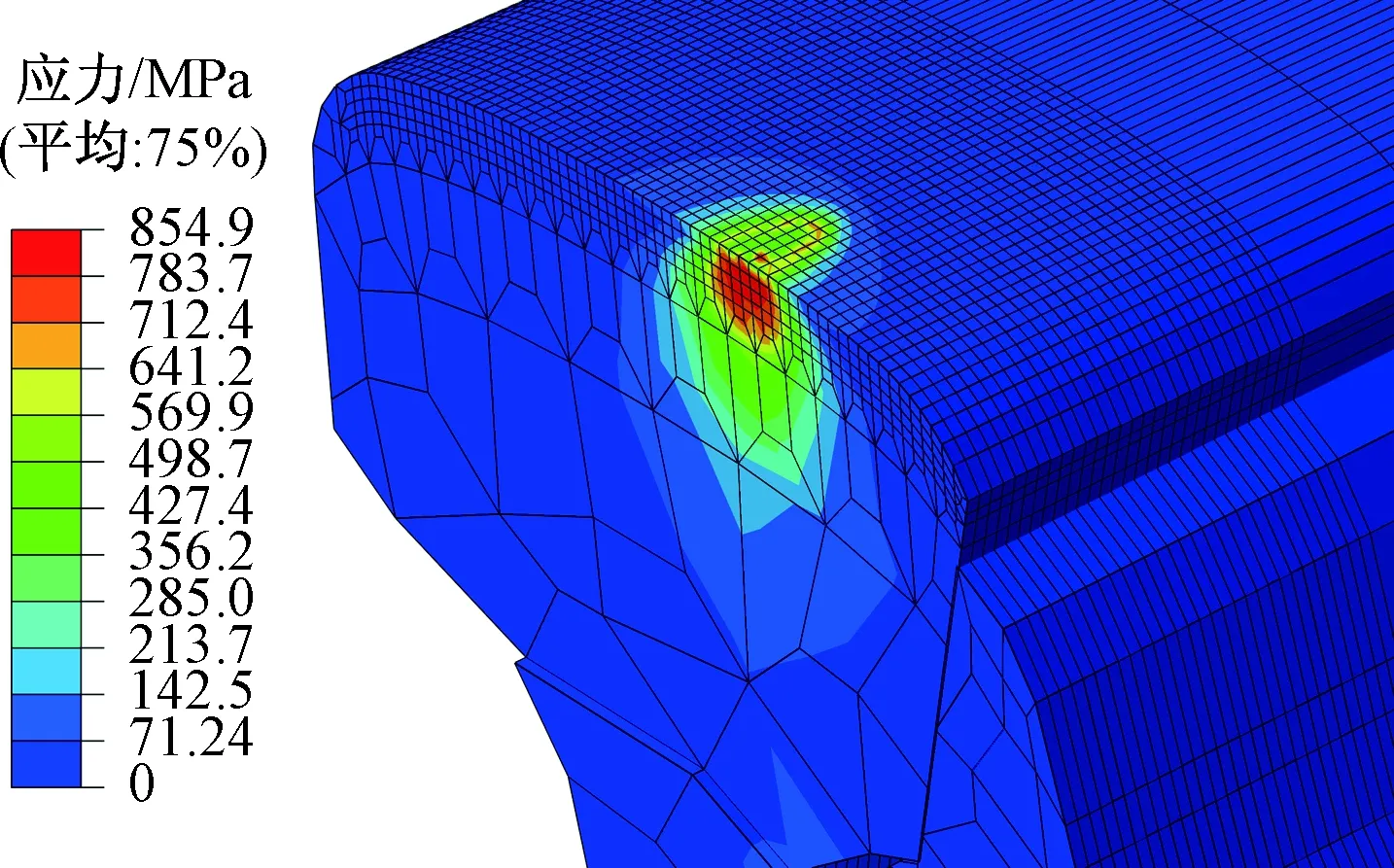
图9 等效应力分布

调节器在轴重的作用下，接触区域内有明显的应力集中现象，且最大等效应力在钢轨表面以下 2～4 mm位置处出现，从最大等效应力中心处向外辐射状扩散应力逐步减小。由于横移量的不同，轮轨接触状态不同，应力集中分布范围(分布图中红色区域)的大小不同。

2.2.1 横移量对等效应力的影响

在5个不同横移量下进行有限元计算，并将计算所得的最大等效应力值绘于图10。

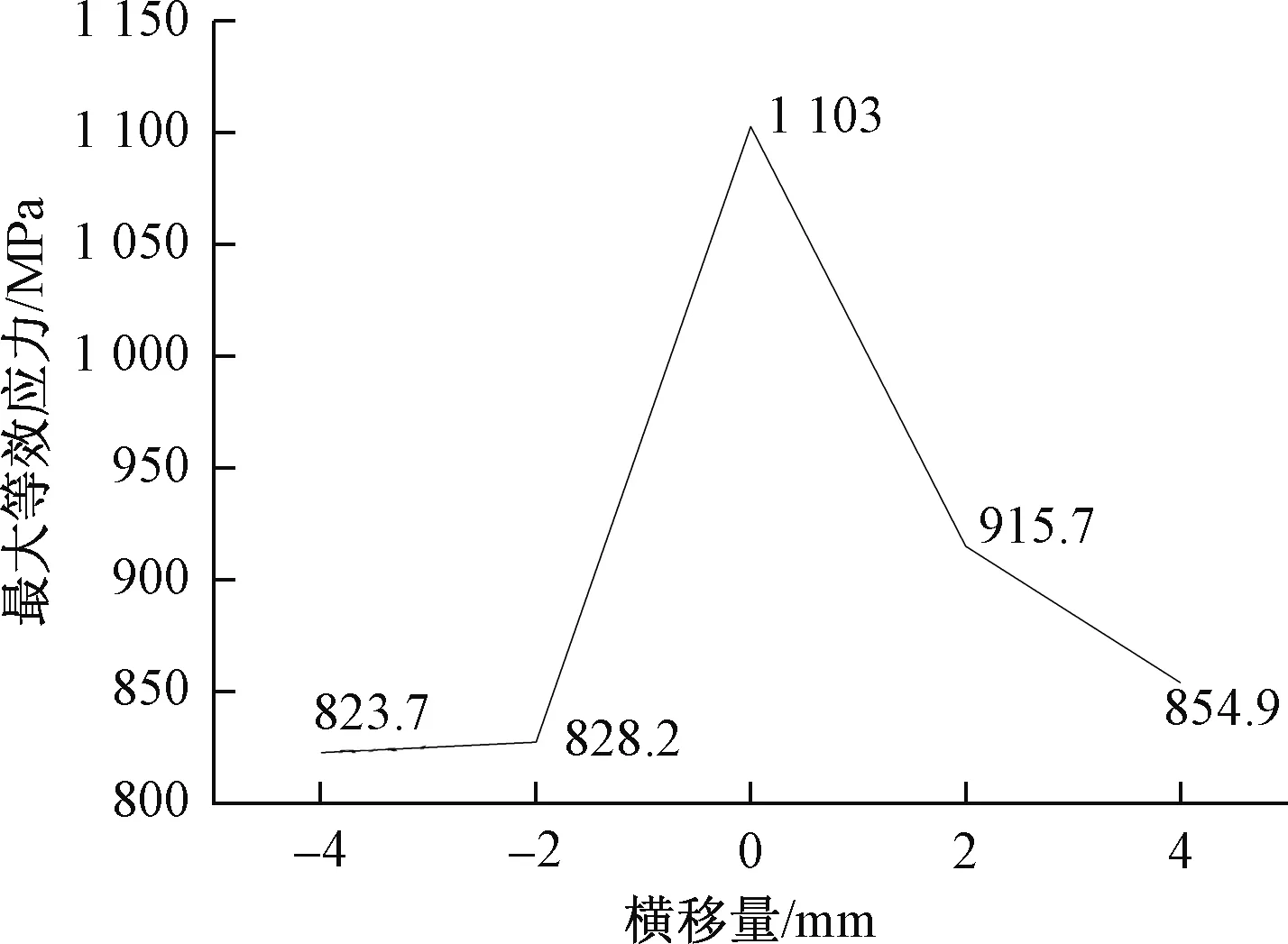
图10 不同横移量的最大等效应力值

每个横移量下受到的最大等效应力均超过了车轮材料的屈服极限689.6 MPa,因此在轮轨接触中发生塑性变形。在对中位置时受到的最大等效应力值为1 103 MPa，左右移动车轮时的最大等效应力值波动较大。

2.2.2 轴重对等效应力的影响

图11列出3个轴重工况下的最大等效应力值。18 t轴重工况下的等效应力最大，16、20 t轴重工况下的最大等效应力基本相同，呈明显的对称分布，合理的设置轴重可有效地减缓轮轨磨耗。

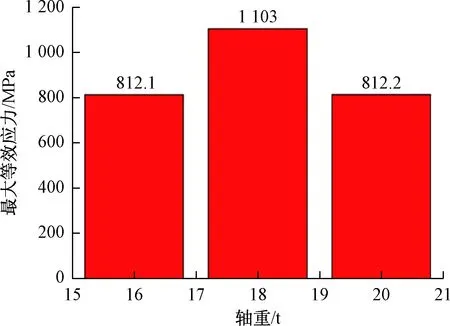
图11 不同轴重下的最大等效应力

2.3 等效塑性应变

轮轨接触的最大等效应力超过了材料的屈服极限，产生塑性变形，分析轮轨等效塑性应变可探究港铁车轮轮对与60E1钢轨单向伸缩调节器的轨道部件最易产生病害的位置。

轮轨接触的等效塑性应变分布基本一致，如图12所示，以横移量为-2 mm时为例分析等效塑性应变分布，等效塑性应变分布情况与等效应力相一致，等效应力大的位置塑性变形越明显，等效塑性应变也越大。

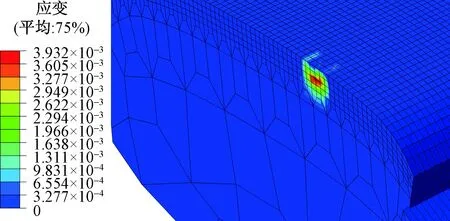
图12 等效塑性应变的分布

2.3.1 横移量对等效塑性应变的影响

不同横移量下的最大等效塑性应变如图13所示。在对中位置时，最大等效塑性应变的值在5个位置中最大，横移量为-2 mm和横移量为 +2 mm 的最大等效塑性应变相同均为3.932×10-3mm，而横移量为-4 mm与横移量为+4 mm时的最大等效塑性应变相差2×10-6mm。最大等效塑性应变随着横移量的增加，以对中位置为中心呈对称变化趋势。

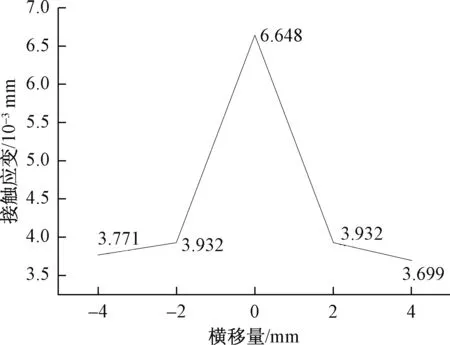
图13 不同横移量下的最大等效塑性应变

2.3.2 轴重对等效塑性应变的影响

等效塑性应变的分布与该工况下的等效应力分布相对应，最大等效应力处出现最大的等效塑性应变。不同轴重下的最大等效塑性应变如图14所示。最大接触应变在轴重工况18 t时6.648×10-3mm，随轴重的改变以轴重18 t为中心呈对称分布。

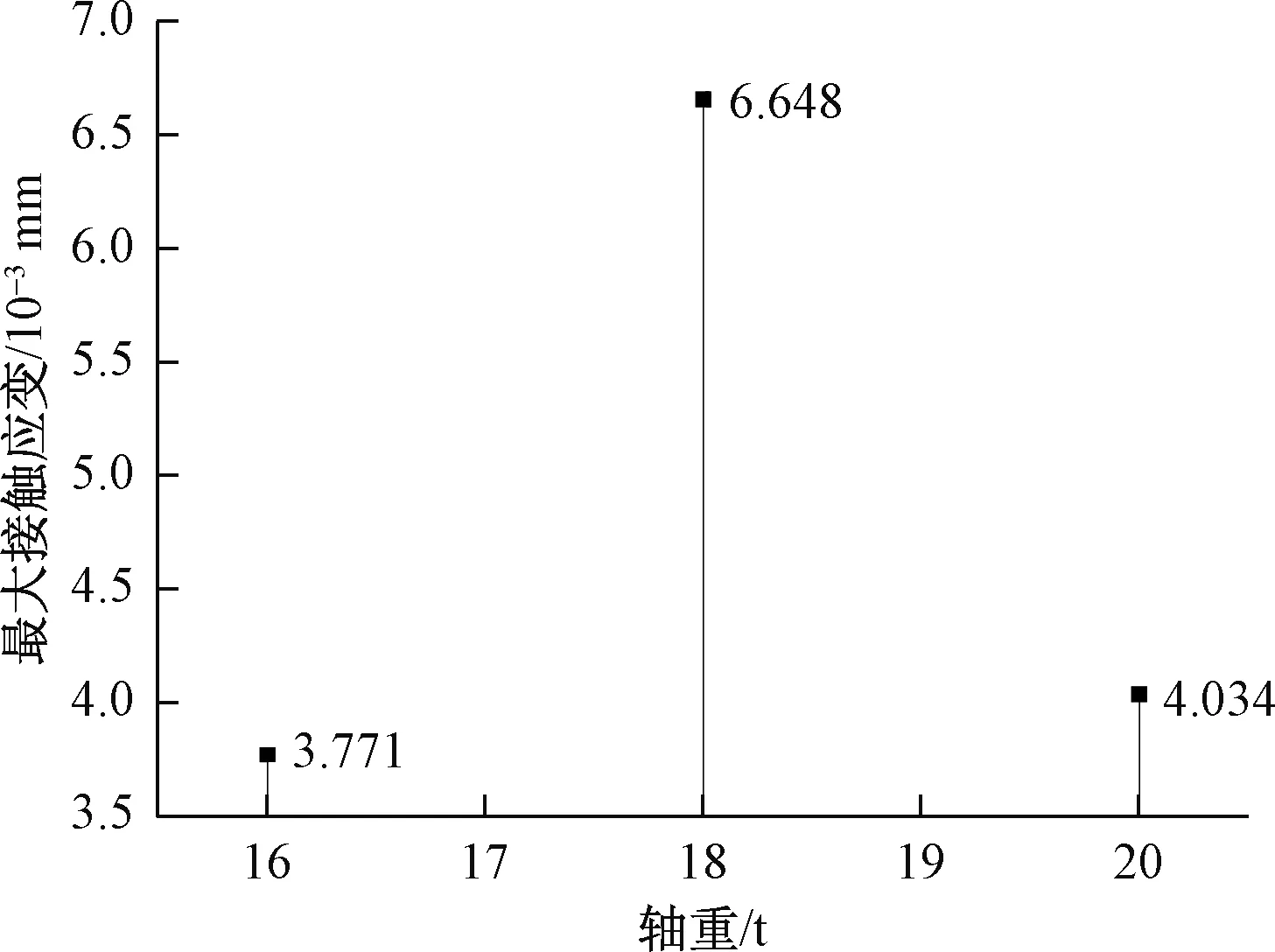
图14 不同轴重下的等效塑性应变

结合等效应力与接触应变分析根据钢轨的接触应变分布，钢轨的病害易出现在轨面以下2～4 mm 处，合理的轴重能减少病害的产生。

3 结论

运用有限元仿真计算的方法，针对港铁车轮与60E1钢轨单向伸缩调节器的接触做了深入的研究，分析接触斑、等效应力及等效塑性应变的变化，得出以下结论：

1)接触斑面积随着横移量的改变以对中位置为中心呈现对称变化规律，随轴重的增大而增加。最大等效应力随横移量与轴重的改变，呈现处相似的变化规律，即在对中位置和18 t轴重时拥有最大值，合理的安排轴重将有助于减缓轮轨的磨耗。

2)在对中位置，轴重为18 t时，接触斑面积为79.5 mm2，等效应力为1 103 MPa，等效塑性应变为6.648×10-3mm，接触斑面积为五个横移量中最小，等效应力与等效塑性应变反而为最大；该接触情况下，将加速轮轨磨耗。

3)最大等效应力和最大接触应变均产生于轨面下方2～4 mm处，此处易出现钢轨病害，因此应着重对轨面下2～4 mm进行探伤。